例谈小学数学教学中“图”的使用
周琳
摘 要:儿童以具体形象思维为主,因此,儿童的数学学习离不开“图”(图形、图像等)的帮助。小学数学教学中,教师要注意利用贴近生活的情境图、表示事物的示意图、表征数量的几何意义图、表征空间形式的几何图、梳理内容关系的思维导图等“图”来引导学生学习。
关键词:小学数学;情境图;示意图;几何意义图;几何图
儿童以具体形象思维为主,因此,儿童的数学学习离不开“图”(图形、图像等)的帮助。小学数学教学中,教师要充分利用“图”来引导学生学习。具体来说,要注意以下几类“图”的使用。
一、贴近生活的情境图的使用
这里的情境,包括有“物(人)”有“事”的复杂情境与有“物(人)”无“事”的简单情境。情境图贴近生活,贴近数学的源头,可以把抽象枯燥的数学内容变得生动有趣,帮助学生形成用数学的眼光观察现实世界的意识。现行各版小学数学教材,都在新授例题和巩固练习中加入了大量的情境图。教学中,教师可以直接出示情境图(包括但不限于教材中的图),引导学生提取生活经验或开展实践活动,进而发现数学知识、解决数学问题。
例如,对于“满10进1”“退1作10”的算理,可以通过小棒图和计数器图(如图1所示)这样的简单情境图来帮助学生理解,并从中抽象出数位,发展出相同数位对齐的竖式计算方法。
再如,在图形概念的教学中,可以出示学生熟悉的实物的图片,引导学生抽象出长方形、平行四边形、三角形、圆等平面图形,以及长方体、圆柱、球等立体图形。
二、表示事物的示意图的使用
示意图是情境图的简化。现实情境中的事物可以用示意图表征,如用一个点(或圆圈、方框、三角等)代表一个事物,用两点之间的连线代表两个事物之间的关系。由此,可以方便地发现事物的数量属性及其关系。[1]教学中,教师可以引导学生根据非图形语言表述的事物画出示意图,从而理解数学意义,解决数学问题。
比如,教学一年级的“比多少”内容时,教师引导学生根据语言描述画出表征实物的示意图(如图2所示),从而方便地看出谁比谁多几或谁比谁少几。如果学生一下子看不出,还可以进一步引导学生连一连表征实物的示意图(使其一一对应),标注同样多的部分以及多的部分或少的部分(如图3所示)。
当然,其逆向问题“已知谁比谁多几或谁比谁少几,以及一方有多少,求另一方有多少”,也可以画出示意图来解决(如图4所示)。再发散一下,还可以解决“一方给另一方多少后两方一样多”的问题(如图5所示)。
再如,对于常见的“8行8列的方阵最外圈有多少人”的问题,学生如果不画图,而凭直觉或想象,很有可能得出“8×4=32(人)”的答案。对此,教师可以让学生画示意图,并思考“是不是一定要把8行8列的人全画出来”。学生能想到可以用一个圆圈代表一个人,且只要画出“方阵最外圈的人”(他们排列在一个正方形的四条边上)。在画示意图(如图6所示)的过程中,学生发现,只有第一条边要画8个点,与其相邻的两条边只要再画7个点(否则就不是正方形),而最后一条边只要再画6个点。由此,得出最外圈有28人。
这时,教师可以追问:为什么比最初的32人少了4人?引导學生在画出的示意图上圈出每边的8人(如图7所示),并发现原因:四个角上的人都被算了2次,要把多算的一次去掉,所以是32-4=28(人)。由此,学生发现了解决该问题的关键,对该问题中数量关系的理解更加深入。
此外,对于没有现实情境的纯数量关系(计算)问题,如“从1开始的连续奇数求和”问题,也可以引导学生通过画示意图来解决。
三、表征数量的几何意义图的使用
几何意义图是示意图的进一步抽象(数学化)。现实情境中事物的数量属性、抽象之后数学情境中的数,可以用几何意义,如线段的长度、平面图形的面积或立体图形的体积等(即相应几何量计量单位的个数),直线、平面或空间中的点(即基于某一“标准”的几何位置,与“标准”构成一定的几何量关系)来表征。由此,很容易发现数量关系以及运算结果。[2]
这类图形中最常见的是通过线段的长度表征数量的线段图。通常来说,比较小的整数(离散)数量,既可用示意图表征,又可用线段图表征。比如,上述“一方给另一方多少后两方一样多”的问题,也可用线段图来表示(如图8所示)。再如,上述“8行8列的方阵最外圈有多少人”的问题,也可用线段图来表示(如图9所示)。
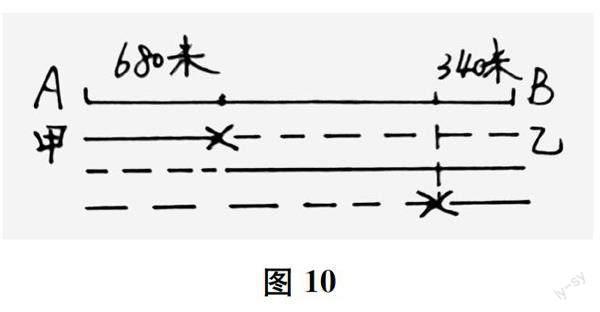
对于比较大的或非整数(连续)数量,常常只能用线段图表征。特别是对于一些数量关系复杂的问题(如相遇问题、追及问题),还要用线段图清晰地表示出数量变化(数量关系形成)的过程。比如“两次相遇问题”:甲、乙两人分别从A、B两地同时出发相向而行,他们分别到达B、A两地后都立即返回,已知第一次相遇处离A地680米,第二次相遇处离B地340米,则A、B两地相距多少米?这类问题没有给出速度和时间,常让学生不知所措,完全没有思路。对此,可以引导学生耐心地阅读题题目条件,仔细地利用线段图画出甲、乙两人的行走路径,得到图10(为了表意清晰,用虚线、实线来区别甲、乙两人的行走路径;由于一开始不能确定谁走得快、谁走得慢,可以先作假设,再根据画出的图来调整)。从图中不难看出:第一次相遇时,甲、乙合走了一个全程,甲走了680米;第二次相遇时,甲、乙合走了三个全程(这是“两次相遇问题”的普遍规律),甲走了一个全程加340米。进一步分析数量关系可知,因为速度恒定,所以甲、乙合走三个全程的时间是合走一个全程的时间的3倍,所以第二次相遇时甲走的路程是第一次相遇时甲走的路程的3倍,即680×3=2040(米)——这里抓住了时间这个联系甲、乙的共同量。由此,便豁然开朗:AB的距离就是甲走的路程减去340米,即2040-340=1800(米)。
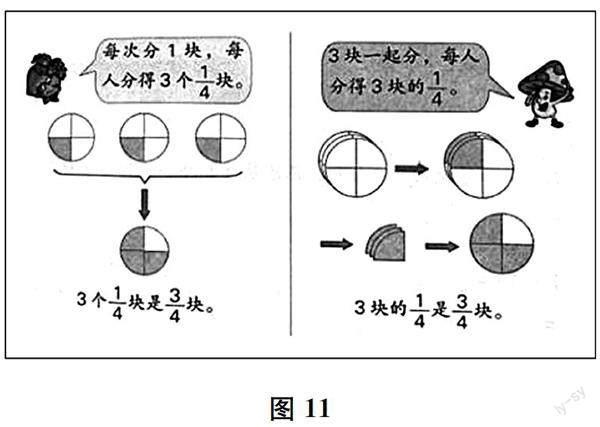
此外,通过图形的面积表征数量的方形图、圆形图等,也比较常见,尤其是在表征分数时(如图11所示)。
四、表征空间形式的几何图的使用
现实情境中事物的空间形式可以直接抽象为几何图。由此,更容易研究其中的数量关系。[3]这里的几何图是一种特殊的情境图,即由情境图抽象得到的图;也是一种特殊的几何意义图,即不是数量中有几何意义,而是几何中有数量意义。对几何图,主要是研究其中的数量关系。教学中,教师特别要引导学生注意这类图的割补变化。这是教学的难点所在。
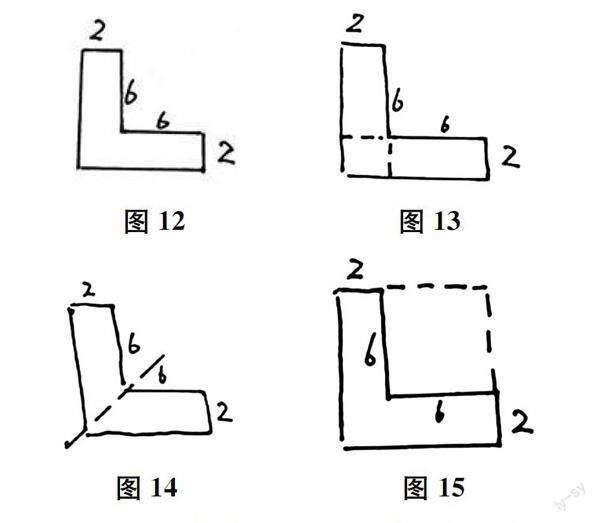
比如求不规则图形面积的问题:求图12所示图形的面积。对此,可以引导学生通过分割转化为规则图形来求面积(如图13、图14所示),或者通过拼补转化为规则图形来求面积(如图15所示)。
再如平面图形变化的问题:把边长为5米的正方形的每条边都延长2米,求增加部分的面积。对此,学生容易画出如图16所示的错误图形。教师可以引导学生回看题目条件,检查所画图形,发现这样画把边长为5米的正方形每条边都向两个方向各延长了2米,一共延长了4米。由此,学生不难发现正确的画法:向一个方向各延长2米(如图17所示)或向两个方向各延长1米(如图18所示)。
五、梳理内容关系的思维导图的使用
思维导图(树型图),是围绕一个中心内容向外发散,运用图文并重的方式,把零碎、散乱的内容有层次、有条理地联结在一起形成的富有个性的网络图,是一种基于事物之间联系进行的“再创造”。小学生对事物(尤其是知识)联系的认识还不够,绘制思维导图时需要教师的示范和引导。
在小学低年段,思维导图更多地应用于抽象数学知识的生动理解,可以引导学生结合生活经验展开联想和想象。在小学中高年段,思维导图较多地应用于单元数学知识的系统整理(如图19所示),可以引导学生抓住知识关系展开联想和分析。
需要说明的是,本文重点梳理了小学数学教学中常用的几类图,从现实与抽象、数量与空间、知识点与知识体系等多个角度考虑,并不是同一维度的图形分类。
参考文献:
[1][2][3] 程茂山.也谈几何直观的培养[J].教育研究与评论(小学教育教学),2022(9):70,70,71.

