翼身融合布局与传统布局飞机结冰特性对比分析

王灏东，桑为民，邱奥祥，李栋

西北工业大学，陕西 西安 710072

结冰是危害飞机飞行安全的重要因素，由结冰导致的飞行事故常常发生。机翼和发动机[1]等部位的结冰问题会对飞机的气动特性产生剧烈影响，从而降低飞行质量，情况严重时甚至会导致机毁人亡等危害，因而受到人们的广泛关注。目前国内外的研究人员致力于研究过冷大水滴和冰晶结冰[2]，为防/除冰方案设计提供了可靠依据。

对飞机结冰特性的分析研究方法主要分为数值模拟方法和试验方法。数值模拟方法[3-4]具有计算效率和精度较高、周期短、容易操控计算条件、经济性高等优点，是研究飞机结冰的重要手段。国内外研究人员在结冰数值模拟领域取得了众多成果。V.H.Gray[5-6]研究了NACA 65A004翼型结冰过程，分析了带冰翼型气动性能，并提出了预测积冰产生的阻力的经验公式。C.D.Macarthur[7]发展了一种数学模型，可用来计算二维翼型上的霜冰和光冰增长。M.B.Bragg[8]提出了一种能计算水滴轨迹的方法，并对该方法的改进提出了一些建议。C.E.Porter[9-10]研究了D8飞机上影响水滴撞击特性的因素。谭燕[11]采用欧拉方法对某对称楔形翼型结冰过程进行数值模拟，采用Spalart-Allmaras（SA）湍流模型获得流场结果，应用欧拉方法获得冰晶和液滴轨迹结果，并基于Messinger 模型来获得冰形，之后通过NASA-NRC 第139 号试验结果证实了该方法的可行性。张强等[12]利用欧拉法研究了ONERA M6 三维机翼表面的水滴收集系数，将结冰问题拓展到了三维。

本文研究工作对传统布局飞机和新型翼身融合布局飞机的空气流场计算结果与试验结果进行了验证，并将两种布局飞机进行了对比研究分析。基于提出的结冰数值模拟计算方法，对新型翼身融合布局构型的N2A翼身融合体和传统布局的DLR-F4飞机在典型霜冰结冰条件下进行结冰数值模拟，分析结冰特性，并将两者进行对比研究分析，初步探讨新型翼身融合布局飞机和传统布局飞机结冰特性的差异。

1 结冰数值模拟计算方法

1.1 空气流场数值求解

空气流场计算是研究结冰数值计算的基础环节，也是研究水滴撞击特性的关键。对结冰空气流场的计算基于对计算域中Navier-Stokes（N-S）方程组的求解。空气流场在进行流动和传热时，可用控制方程对质量守恒定律、动量定律和能量守恒定律三个方程进行描述。N-S 方程积分形式为

式中，Q为守恒变量；F为对流通量；G为黏性通量；Ω为控制体。

1.2 水滴撞击特性计算

水滴对飞机表面的撞击特性是指水滴对飞机表面的撞击区、撞击量，以及水滴在撞击区内的分布。过冷水滴运动方程的建立方法主要分为拉格朗日法和欧拉法[13-14]。本文基于欧拉法开展研究。

欧拉法的思想是将水滴与空气看作两相流建立控制方程。定义一个水滴容积参数α，建立水滴场的控制方程，其形式上与流场计算的控制方程可保持一致[15]。对于三维计算来说，采用欧拉法计算水滴撞击特性不必在计算区域进行多次插值计算以及数值积分计算，并采用流场计算所用的网格，使水滴场的求解与流场求解在形式上统一，提高了代码开发效率和计算效率[16]。欧拉法将云层中离散的过冷水滴当作连续相处理，并做出相关假设[17]。

欧拉法求解水滴运动特性的连续方程主要有以下几个。

空气连续方程为

水滴连续方程为

式中，ρ为过冷水滴的密度；α为体积因子。

收集系数β为微元表面上水滴的实际收集率与该微元表面上最大可能的收集率之比，是表征结冰表面法向水滴流率的无量纲参数，在欧拉法中其定义式为

式中，u和n分别为结冰表面当地的水滴速度矢量和单位法矢量；LWC 为空气的液态水含量；U为自由流水滴速度大小；αN为水滴的无量纲（量纲一）体积分数。

1.3 结冰热力学模型

基于空气和水滴流场、水滴撞击特性的计算结果，获得机翼表面局部水收集系数，通过对机翼建立结冰模型并求解，得到结冰后的结冰形状。本文采用了考虑初始水膜流动的Shallow-Water结冰热力学模型。

Shallow-Water 结冰模型是基于表面水膜运动而建立的机翼表面结冰模型[18]。在结冰预测研究中，使用Shallow-Water结冰模型进行结冰模拟，该模型水膜流动受三维偏微分方程（PDE）控制，并在结构化和非结构化表面网格上采用稳定的有限体积格式离散。Shallow-Water 模型由质量和能量平衡的两个偏微分方程与动量系统的代数方程组成。模型方程概述主要有以下几个[19]。

质量守恒方程为

式中，ρw为水的密度；hf为水膜高度；u为水膜速度矢量；ṁβ、ṁice、ṁevap为液滴撞击、冻结、蒸发的质量通量。

动量方程为

式中，τ为表面切应力矢量；μw为水动力黏度；a为水膜受到的累积加速度（离心力、科里奥利力、重力）。

能量方程为

式中，T为取决于霜冰或光冰状态的水膜或冰的温度；Cw为水的比热；Cice为冰的比热；Td为初始撞击的水滴的温度；Lf为水的冻结潜热；Q̇evap、Q̇h、Q̇cond为分别来自蒸发、对流、传导的热通量。

联立上述方程，可将其化简为T和冻结系数n的方程，其中n可表示为

式中，ϕ为水滴能量传递参数；ε为空气能量传递参数；b为相对热因子。

求解得到T和冻结系数n之后，再结合水滴撞击求解得到的结果，积分可得整个翼面上的结冰质量和厚度。

2 空气流场及气动特性验证及对比分析研究

首先，验证翼身组合体布局飞机的空气流场计算。选择美国航空航天学会（AIAA）第二届阻力预测研讨会模型DLR-F4 翼身组合体作为本文传统布局飞机计算模型，并将数值计算研究与AIAA 第二届阻力预测会议文献（DPW2）进行对比验证。计算条件为：马赫数Ma=0.6，雷诺数Re=3×106，参考弦长c=0.1412m。计算模型为对称模型，在对称面上采用对称边界条件，网格总量约为870万个，与参考文献[20]中量级相当。

在不同来流迎角下，数值计算得到的升力系数与试验数据[20]对比如图1所示；在不同来流迎角下，数值计算得到的阻力系数与试验数据[20]对比如图2所示。计算结果与试验数据较相符，验证了空气流场计算方法的准确性。

图1 升力特性曲线Fig.1 Lift characteristic curve

图2 阻力特性曲线Fig.2 Resistance characteristic curve

然后验证翼身融合飞机空气流场。本节计算模型选择5.8%缩比的N2A翼身融合体，并与NASA兰利亚声速风洞试验结果[21]进行对比验证。参考文献试验条件为：马赫数Ma=0.2，雷诺数Re=6.6×106，参考弦长c=1.538m。

计算模型为对称模型，采用半模计算，在对称面上采用对称边界条件来减少计算量。在0°～10°范围内不同来流迎角下，对比数值计算升力系数与试验数据[20]的误差。为保证计算误差符合要求，采用S-A 湍流模型进行计算，本文N2A 翼身构型计算网格总量约为2800 万个，与参考文献[22]网格量级相当。

图3 对比了不同来流迎角下，数值计算升力系数与试验数据[21]；图4对比了不同迎角下所对应的升力系数、阻力系数的值与试验数据[21]，计算结果与试验数据均对比良好，验证了空气流场计算方法的准确性。

图3 升力特性曲线Fig.3 Lift characteristic curve

图4 升阻极曲线Fig.4 Lifting resistor curve

从计算结果与试验结果的对比可以看出，本文所采用方法的计算结果与文献数据均对比良好，误差均在允许范围内，验证了本文计算方法的准确性。

图5 所示的是DLR-F4 飞机在来流迎角为5.384°时的压力分布云图。从图5中可以看出，传统布局飞机DLR-F4飞机机翼前后缘处上下表面压力差较大，机身处上下表面压力系数较为相近，可知传统布局飞机DLR-F4 升力几乎都由机翼提供，机身提供的升力可忽略。

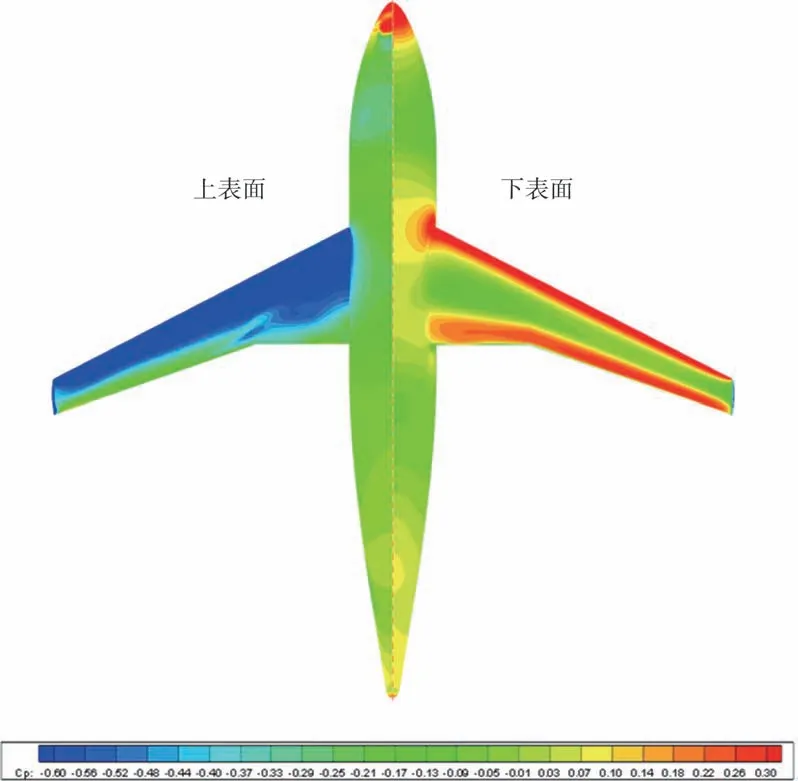
图5 DLR-F4飞机上下表面压力分布云图Fig.5 DLR-F4 aircraft upper and lower surface pressure distribution cloud chart

图6所示的是N2A翼身融合布局飞机在来流迎角为5°时的压力分布云图。从图6 中可以看出，与传统布局飞机不同的是，翼身融合飞机机身、机翼和翼身融合处都是升力面。从压力系数分布云图中可知，翼身融合布局飞机全机都是升力面，机翼前缘和机身头部位置上下表面的压力系数差距都十分明显。

图6 N2A飞机上下表面压力分布云图Fig.6 N2A aircraft upper and lower surface pressure distribution cloud chart

3 结冰数值模拟过程及结果对比分析研究

3.1 DLR-F4飞机表面冰形生成及其特征

选择DLR-F4 作为本节飞机计算模型，但DLR-F4 带冰形飞机模型目前还未公开，采用结冰软件FENSAP-ICE来构造DLR-F6 翼身组合体的冰形。计算条件为：大气压力为39000Pa，雷诺数Re=3×106。第2节通过与试验结果对比，验证了空气流场计算方法，保证了计算结果的准确性。由于结冰通常都是发生在飞机低速起降和爬升等的穿云飞行过程中，对应的马赫数较低，所以结冰计算工况选择典型的霜冰工况，见表1。本文采用单步法对DLR-F4翼身组合体进行结冰数值模拟。

表1 结冰计算条件Table 1 Ice calculation conditions

在进行N-S 方程求解过程中，对边界层内的流场进行模拟时，结构网格有着非结构网格不可比拟的优点，计算网格采用结构化网格，与前文计算网格一样，网格图如图7所示。网格总量约为870万个，机身网格较粗，机翼前缘处为主要结冰区域，需要加密网格更好地捕捉流场信息，以良好地描述冰形，故加密此处网格。

图7 DLR-F4计算网格Fig.7 DLR-F4 computing grid

图8所示为DLR-F4飞机表面生成的冰形图，虽然结冰时间只有360s，但是在机翼前缘和机头部位仍形成较大尺度的结冰。

图8 DLR-F4冰形生成图Fig.8 DLR-F4 ice formation diagram

图9 为机翼沿展向在z/b=20%，z/b=50%，z/b=80%三个不同截面的冰形图，其中z为展向长度，b为半展长，各截面冰形呈现流线型，且相对翼型尺寸由翼根至翼尖逐渐变大。

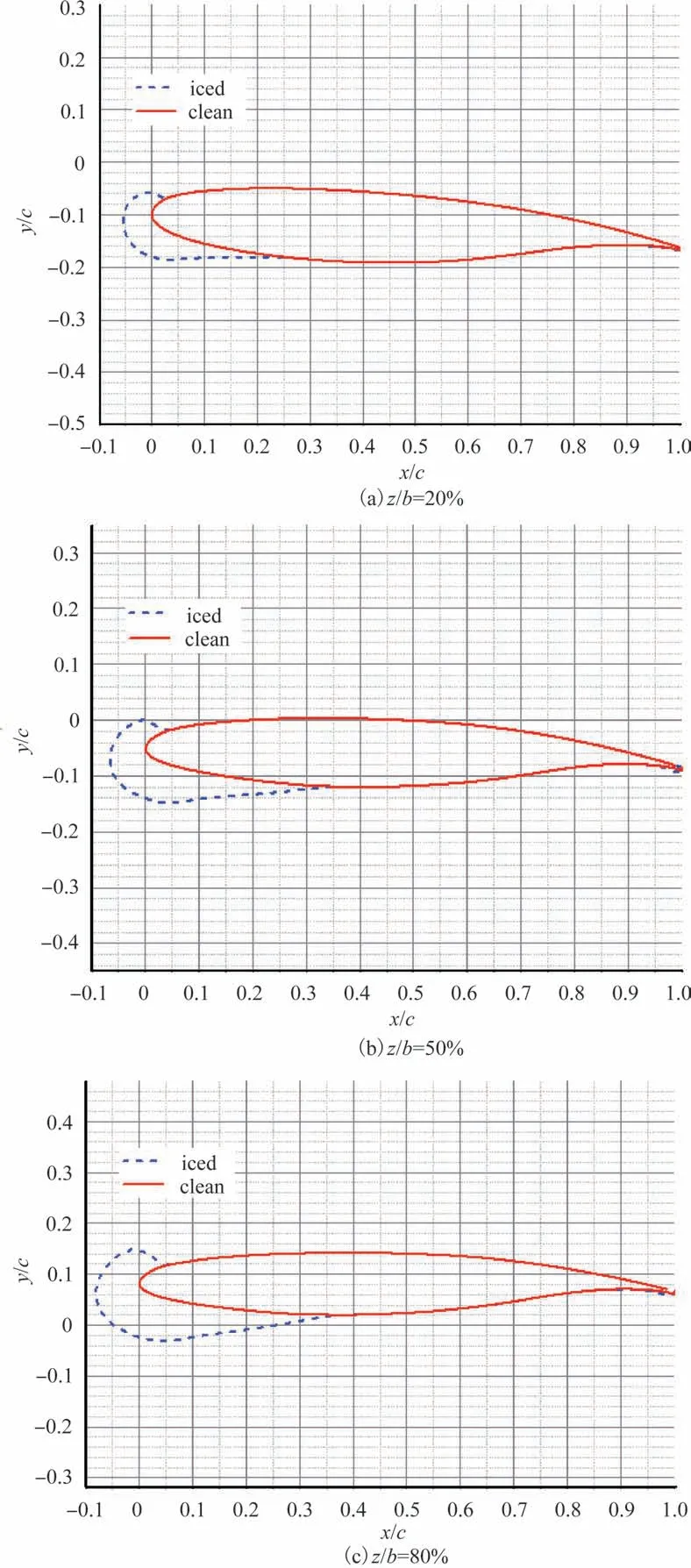
图9 DLR-F4飞机不同截面冰形图Fig.9 Ice diagram of different sections of DLR-F4 aircraft

3.2 N2A飞机表面冰形生成及其特征

选择5.8%比例的N2A翼身融合体作为飞机计算模型。目前对N2A 翼身融合布局结冰数值模拟的公开文献尚未出现，采用结冰软件FENSAP-ICE来构造N2A翼身融合布局飞机的冰形。

本节结冰计算工况选择典型的霜冰工况，见表2。采用单步法对N2A翼身组合体进行结冰数值模拟。

表2 结冰计算条件Table 2 Ice calculation conditions

计算网格采用结构化网格，与前文计算网格一样，网格图如图10 所示。而新型翼身融合布局构型将机身融合成机翼的一部分，使飞机的升阻比显著提高，但这一部分机身迎风面也变成飞机主要结冰区域，故进行机身头部加密。

图10 N2A计算网格Fig.10 N2A computing grid

图11所示为N2A飞机表面结冰图。根据计算条件，虽然结冰时间只有360s，但是在机翼前缘仍形成较大尺度的冰。与传统翼身组合体构型由机翼和机身两个部件结合而成，机翼前缘明显是主要结冰区域不同，该构型飞机机体成为一个完整的升力面，升力面上的结冰区域比较模糊，从大约沿展向在z/b=10%位置处发生结冰现象。

图11 N2A冰形生成图Fig.11 N2A ice formation diagram

图12 为机翼沿展向在z/b=20%，z/b=50%，z/b=80%三个不同截面的冰形图，从图12 中能看出，各截面冰形附着在翼型表面，为流向冰，相对翼型尺寸由翼根至翼尖逐渐变大。

3.3 DLR-F4飞机与N2A飞机结冰特性对比分析

图13 和图14 所示分别为DLR-F4 和N2A 飞机表面的冰生长质量流量图。从图13与图14中可以看出，翼身组合体飞机的机翼前缘与机头是结冰速率最快的区域，但N2A翼身融合布局飞机结冰速率最快的区域为机头、翼身融合段与机翼的前缘。

图13 DLR-F4表面冰生长质量流量Fig.13 DLR-F4 surface ice growth mass flow

图14 N2A表面冰生长质量流量Fig.14 N2A surface ice growth mass flow

图15是DLR-F4翼身组合体结冰后飞机上下表面的冰形图。传统翼身构型飞机由机翼和圆筒形机身两个部件结合而成，飞机的机身和机翼区别明显。如图15 所示，飞机的迎风面发生了结冰现象，机翼作为飞机主要升力面生成的冰形最厚，机翼前缘是主要结冰区域。

图15 DLR-F4翼身组合体结冰后上下表面的冰形图Fig.15 Ice diagram of the front and rear surfaces of the DLR-F4 wing-body combination after freezing

图16 是N2A 翼身融合体结冰后前后表面的冰形图。新型翼身融合布局构型为了减小翼身之间的干扰阻力和诱导阻力，减小飞机的总阻力，将机翼与翼身融合，使得整个飞机机体成为一个大的升力面。如图16所示，飞机的迎风面发生了结冰现象，由于整个飞机机体为飞机提供升力，翼身融合体整机前缘是主要结冰区域。

图16 N2A翼身融合体结冰后上下表面的冰形图Fig.16 Ice diagram of the front and rear surfaces of the N2A blended-wing-body after freezing

从计算结果中可以看出，相较于DLR-F4翼身组合体，N2A 翼身融合体在机身、翼身融合段和机翼前缘均发生结冰现象。在后续的结冰研究和防/除冰研究中，需要考虑翼身融合布局飞机全翼面上的结冰问题。

4 结论

本文针对两种布局飞机结冰，首先构建了结冰数值模拟方法，验证了两种布局飞机的空气流场，之后通过数值计算方法针对新型翼身融合布局构型和传统布局飞机进行霜冰结冰数值模拟，对比分析其结冰特性，并得出以下结论：

（1）验证了DLR-F4与N2A空气流场计算方法，并对比分析气动特性，得出传统布局飞机升力由机翼提供，翼身融合布局飞机升力由机翼和机身共同提供，为后续结冰特性分析研究奠定良好基础。

（2）对翼身融合布局构型N2A在典型霜冰结冰条件下开展结冰数值模拟，分析其结冰区域及表面冰生长质量流量，并将N2A 结冰特性与传统翼身组合体DLR-F4 结冰特性进行比较，发现需要考虑机翼与机身融合处的结冰及防/除冰问题，翼身融合布局飞机机翼部分的结冰与传统布局飞机较为相似。