螺栓群连接焊接十字箱型装配式塔机基础

杨建晖，池政恒

（1.福州职业技术学院，福建 福州 350108；2.福建力诚建设工程有限公司，福建 福州 350000）

由于同时具备竖直和水平运输功能，塔机在建筑行业具有很广泛的使用。传统塔机基础结构简单，施工方便，但亦存在不足：首先，基础尺寸大，工序多，受气候、地基承载力等条件制约，施工周期长；其次，基础为一次性使用的临时性结构，费用高，单个基础施工及凿除费用超过5 万元。传统基础资源浪费严重，废弃物及施工噪声染环境，不符合当前我国“绿色施工”、“可持续发展”的时代发展要求。

笔者根据多年工程实践经验，曾提出螺栓群连接焊接十字工字钢塔机基础。该基础具有连接方便、刚度大、施工周期短、虽一次性投资较高但摊销使用费较低、可回收并重复利用的优点。但与同截面尺寸箱梁相比，工字钢梁截面惯性矩、抵抗矩相对较小，以1 000×400×20mm 工字钢及1 000×400×20×20mm 箱梁为例，工字钢梁惯性矩、抵抗矩仅为箱梁的78.3%，则相同塔机荷载作用下工字钢截面钢梁存在较大变形和内力。因此，在原工字钢塔机基础上进一步提出螺栓群连接焊接十字箱型装配式钢基础。与工字钢基础相比，相同截面尺寸箱梁基础可承受更大荷载且刚度更大，而相同上部荷载则可减小箱型钢基础截面尺寸。

1 螺栓群连接焊接箱型十字装配式钢基础

图1 为焊接十字箱型装配式塔机基础型式。

图1 螺栓群连接十字箱型塔机基础

钢十字塔机基础长、宽一般超过4m，不符合我国道路运输法规定，需先将十字基础其中一条单梁拆分成2 段或3 段，运输到现场后再进行组装。依据结构力学原理，箱梁拆分处应避开钢梁受力关键部位，即弯矩、剪力最大位置，如塔机柱脚等。箱型钢基础力学性能分析及拆分位置可参考文献[1-2]，不再复述。

本螺栓群连接十字箱型基础接头方式如图2所示，采用两块连接钢板及螺栓群将分段箱梁连接成整体。因箱梁腹板间距较宽，常规A、B、C 级普通螺栓以及承压型大六角高强螺栓副无法满足要求，高强或普通对拉螺栓需要定制或自加工，螺栓数量满足抗剪、抗拉强度即可。螺栓群连接的螺栓端距、孔距可综合考虑文献[3-4]确定，并满足文献[2，5]相关要求。可采用混凝土预制块或预应力锚杆作为基础抗倾覆措施。

图2 螺栓群连接大样图

采用螺栓群连接的十字钢梁整体性好、刚度大，无须专业班组配合，基础组装、螺栓连接和拆卸方便，达到使用年限后报废的十字钢梁及废弃更换的螺栓还可回收利用，具有良好的经济效益和社会效益。

2 箱梁最优化设计

2.1 箱梁腹板高度优化设计

焊接组合箱型钢梁是塔机基础的主要受力构件，其设计品质直接关系到塔机的安全性、经济性。本章节拟结合桥式起重机、门式起重机钢梁优化设计[6-7]及工程最优化方法[8-11]，以钢梁腹板面积/截面总面积为设计变量，在总钢板用量与箱梁腹板高厚比约束条件下对焊接箱梁惯性矩I、抗弯模量W进行优化，寻求箱梁最理想截面强度和刚度，即在总成本一定下力求钢梁最佳工作性能。

2.1.1 塔机焊接十字箱梁截面尺寸和参数

焊接箱梁截面尺寸和参数如图3 所示。

图3 焊接箱梁剖面

2.1.2 箱梁理想化截面惯性矩、抗弯抵抗矩

为简化计算，假设箱梁上翼缘板、下翼缘板面积集中于板厚的零线上，令α为腹板面积与箱梁截面总面积比系数，α=Sf/S；β为箱梁腹板高厚比，β=hf/tf。则箱梁截面惯性矩I、抗弯抵抗矩W分别为

据α=Sf/S=hf tf/S可得hf=αS/tf，而由β=hf/tf可得hf=βtf，则hf2=hf hf=αS/tf×βtf=Sαβ，代入式（4)得

2.1.3 箱梁理想惯性矩I、截面抵抗矩W的优化

箱梁塔机基础的外荷载经计算确定后进行截面设计。最优化设计原则是在满足强度、刚度、稳定的约束条件下具有最小截面积S，使单位长度下箱梁成本最低，同时，最优腹板高可使钢梁截面惯性矩I、抵抗矩W达到极值。

以α为设计变量，且当S和β为定值时，对式（5)和式（6)求导得

式（9)和式（10)说明在截面总面积S一定时，有明确的腹板高厚比β（以hf/tf的数值比及加劲板保证箱梁的局部稳定)，当Sf/S=3/4 时，箱梁的刚性最好，即钢梁抵抗弯曲的性能最好，而当Sf/S=1/2 时，箱梁抗弯模量最大，材料强度利用最好，并能求得梁高最优解。

将式（5）、式（6）分别除以式（9）、式（10），有

对α从0～1 取值，由式（11）、式（12)可得表1 数值。

表1 箱梁截面优化结果表

由表1 可得到如下结论。

1）箱梁截面惯性矩、抵抗矩随着α增大先增大后减小，存在极值。当α取0.75 时，钢梁截面惯性矩I 达到最佳值；当α取0.5 时，截面抵抗矩W达到最佳值。

2）当α=0.65～0.85 时，钢梁截面惯性矩I在最优值98%内；当α=0.4～0.6 时，截面抵抗矩W亦在最优值98%内。

3）当α=0.631 时，两条曲线相交，此时钢梁截面惯性矩I和抵抗矩W都在最优值的97.4%内。

由此，可依据箱梁外荷载选择适当α值，然后采用截面积极小值S和确定的β求解截面最佳惯性矩I和抵抗矩W，再按规范要求调整α值，同时，保证截面惯性矩I和抵抗矩W满足要求。

由材料力学I=M/（Ey)可知，钢梁弯矩M、容许挠度y确定后即可推算截面最小惯性矩I。以前述简化计算参数为例进行计算，M=669.1kNm，容许挠度y=l/500=10mm，则钢梁惯性矩=3.25× 108mm4。

由文献[4]可知，焊接组合钢箱梁应考虑翼缘板、腹板的稳定性，以免发生局部失稳，从而影响箱梁的强度、刚度及整体稳定性。翼缘板局部稳定要求受压翼缘板的钢梁腹板之间无支承，且宽度与其厚度比不超过40δ；钢梁腹板局部稳定与腹板受力、腹板高厚比和材料性能有关，局部压应力、剪应力和弯曲应力作用下腹板高厚比应分别低于84δ、104δ和174δ，其中δ为焊接箱梁钢材钢号修正系数，其值为235 与钢材牌号中屈服点比值的平方根。

依据上述要求，塔机焊接箱梁基础取β=100。由式（9)可得hutl=975mm，取hutl=980mm。因tf=hutl/β=9.8mm，取tf=10mm，则钢梁腹板面积Sf=19600mm2。S=Sf/α=31061.8mm2，Sy=SSf=11461.8mm2。暂令翼缘板厚度为10mm，则by=Sy/（2×10)=573mm，令by=600mm。

箱梁截面刚度验算，将上述参数代入，可计算1 000mm×600mm×10mm 箱梁的截面惯性矩为4.51×109mm4，满足刚度要求，且有较大富余。可调整α数值，减小箱梁截面尺寸，直至箱梁惯性矩、截面抵抗矩满足要求。

2.2 腹板间距优化设计

上述2.1 节对箱梁高进行了优化设计研究，即荷载作用下有最优梁高，使得箱梁具有良好工作性能。对于箱梁，既定总截面积下可以构成腹板间距不同的箱型截面梁。从力学分析而言，固定腹板高度，不同腹板间距，箱梁惯性矩、截面抵抗矩不变。但实际上，不同腹板间距，翼缘板、腹板内力不同，存在较大差异。以1 000mm×400mm×20mm 箱梁为例，构成腹板间距分别为100mm、200mm、300mm、400mm的箱梁，依据文献[2]将十字箱梁拆分成单梁建立三维实体有限元分析模型（图4）。模型边界条件：限制土体x、y向位移及底面xyz向位移，限制箱梁梁端xy向位移。力学条件：将上部荷载简化为均布荷载施加在塔机柱脚上。浇筑150mm 厚C20混凝土垫层。箱梁内力如图5 所示。

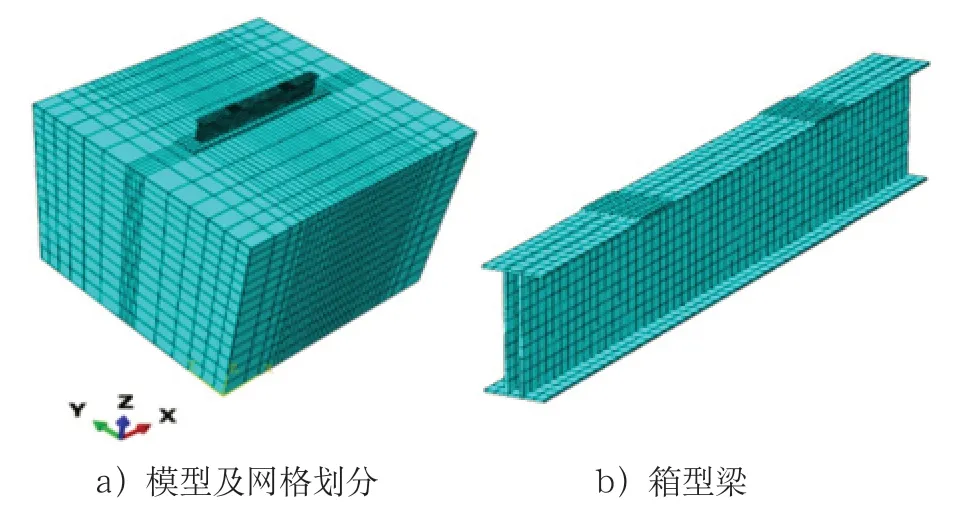
图4 三维实体计算模型图

图5 箱梁计算内力图

从图5 可看出，不同腹板间距箱梁内力基本相同，可见腹板间距对内力影响不大。不同腹板间距箱梁翼缘板、腹板MISES 如图6 所示。

图6 箱梁翼缘板、腹板MISES内力图

可看出，腹板间距为400mm 时，翼缘板、腹板MISES 内力最大；其次，间距为200mm时MISES 内力最小，仅约为100mm 的53%、为300mm 的80%、为400mm 的40%。可见，本研究中腹板间距为200mm 时焊接箱梁性能更佳。

3 结语

提出螺栓群连接焊接十字箱型装配式塔机基础，该基础具有截面抵抗矩大、连接方便、使用摊销成本低、可回收并重复利用的特点。与同截面工字钢相比，具有更高的刚度，变形更小。采用工程最优化设计方法对箱梁腹板高和间距进行了优化设计，当腹板面积为截面面积的0.631时，在成本一定时箱型钢基础可获得最佳工作性能。三维实体有限元分析发现，腹板高度相同而腹板间距不同箱梁弯矩、剪力基本相同，但翼缘板、腹板内力差异较大，本研究中间距为200mm、300mm 时内力较为接近且相对较小，此时装配式箱梁基础性能更佳。