AGV车架有限元分析及结构优化

胡忠义　黄雪涛　许永超　刘子豪　王宪成

摘要：为解决自动导向运输车（automated guided vehicle，AGV）车架在使用中出现裂纹的问题，基于Solidwork建立车架有限元模型，采用Hypermesh对车架弯曲工况、扭转工况、转弯工况、制动工况进行静力学分析，确定危险工况及应力集中部位；增加车架中间纵梁、第3横梁、第6横梁的槽钢厚度，在第3横梁、第6横梁与纵梁交叉处设置加强筋，并对优化后车架的扭转工况、转弯工况进行静力学分析和模态分析。结果表明：优化后车架的扭转工况和转弯工况的最大应力均降低，安全因数符合设计要求；优化后车架不再发生低频共振，解决车架裂纹故障。

关键词：AGV车架；有限元分析；静力学分析；模态分析

中图分类号：U469.2文献标志码：A文章编号：1673-6397（2023）05-0087-06

引用格式：胡忠义，黄雪涛，许永超，等.AGV车架有限元分析及结构优化［J］.内燃机与动力装置，2023，40（5）：87-92.

HU Zhongyi， HUANG Xuetao， XU Yongchao， et al. Finite element analysis of AGV frame and its optimization［J］.Internal Combustion Engine & Powerplant， 2023，40（5）：87-92.

0 引言

自动导向运输车（automated guided vehicle，AGV）是一种应用在园区的自动导航运输工具[1-2]，该车具有自动升降和自行走功能，可实现远程遥控起动、转向、加速和制动，具有操作灵活、安全可靠、适应力强的特点[3]。由于运输车车架承受货物载荷和路面反馈的各种力和力矩，因此，在设计过程中保证AGV车架的强度和刚度非常重要[4-5]。Kim等[6]使用有限元方法对车架进行静态和动态分析计算，优化车架结构，验证了有限元法在优化车架结构上的有效应用；银俊鹰[7]运用有限元软件对自卸车车架进行静力学分析，确定最大应力部位及故障部位；刘伦伦等[8]对车架进行静应力分析和模态分析，实现车架轻量化。国内外学者对货车车架研究较多，但关于AGV车架典型工况下的分析研究较少。

针对某AGV车架在使用中出现裂纹的问题，本文中基于Solidwork软件建立AGV车架有限元模型，采用Hypermesh对4种典型工况进行有限元分析，提出优化方案，并进行静力学分析及模态分析验证，有效解决车架裂纹问题。

1 车架有限元模型

1.1 车架的结构形式

某AGV车架的主体结构由4根纵梁、8根横梁焊接而成，为框架式结构；车架长、宽、高分别为3 000、1 800、140 mm，横、纵梁为厚度为6 mm的C型槽钢；去除车架圆角和倒角，删除不必要的工艺孔及螺栓孔，采用Solidwork软件建模，得到AGV车架的简化三维模型如图1所示。

1.2 车架网格划分

将车架模型导入Hypermesh，抽取模型中面，采用PESHELL进行网格划分[9-10]。网格类型为四面体网格，网格长度、宽度均小于等于10 mm；采用Spotweld焊接对应节点，网格划分结果如图2所示。网格划分后单元数为99 474个，节点数为105 445个；网格检查结果如图3所示，雅可比失效单元数为74个，占比为0.1%，满足雅可比失效单元数占比不得超过5%的分析要求[11-12]。

1.3 材料与载荷

车架材料为Q355B结构钢，以集中载荷的形式将车架装载质量加载至相关总成部件[13-15]，蓄电池组及附件、电机及减速器、车架、液压站及附件、液压支架、货物支撑架、货物载荷加载质量分别为200、75、485、55、150、1 400、600 kg，车架材料参数如表1所示。

1.4 理论基础

将车架结构看作线性自由振动系统[16-17]，不考虑阻尼，车架系统微分方程

式中：p1为第1主应力，p2为第2主应力，p3为第3主应力。

式中：psm为车架仿真计算的最大等效应力，pmax为材料的许用应力。psm不得大于pmax，否则车架易产生塑性变形，导致车架失效。

本文中pmax=345 MPa。根据文献[19]的规定，起重机械主梁安全因数不得低于1.6，车架回弹产生的变形不得大于10 mm。车架设计时，应避免外部激励和车架的固有频率相同，防止产生共振现象[20]，影响车架正常工作。

2 静力学分析

AGV行驶过程中，受到各种力和载荷的作用，车架产生不同程度的弯曲、扭曲及组合变形[21]。以车架纵向为x向，垂向为y向，横向为z向，选取满载弯曲、满载扭转、满载转弯和满载紧急制动4个典型工况，并在y轴施加1.3中所示的各总成部件载荷，使用有限元软件Hypermesh分析不同工况下车架位移及应力。

2.1 弯曲工况

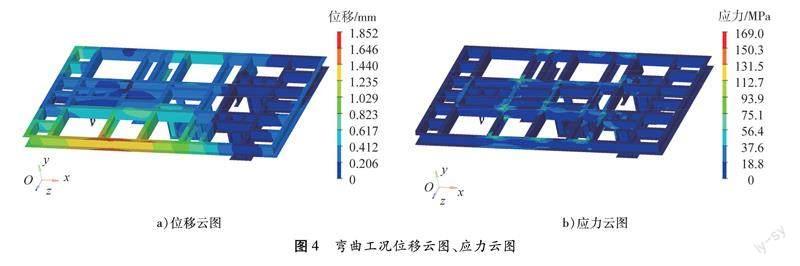
彎曲工况指车架满载静止或匀速行驶时的工况，约束右前、左前、右后、左后4个车轮的x、y、z平动方向，释放x、y、z转动方向。车架弯曲工况位移云图、应力云图如图4所示。

由图4a）可知：车架最大位移发生在车架左侧纵边梁和第3、4横梁处，最大位移为1.852 mm。原因是右侧纵边梁和第3、4横梁上方承载支架和货物的质量，下方承载蓄电池组件的质量，导致左侧边梁翘曲变形，位移较大。

由图4b）可知：较大应力在中间2个纵梁和第3横梁交叉连接处、中间2个纵梁与第6横梁连接处，最大应力为169.0 MPa。原因是上方承载货物和货物支架的质量，下方承载蓄电池组件、液压组件和电机减速机等载荷质量，弯曲工况下安全因数为2.04，车架强度满足设计要求。

2.2 扭转工况

扭转工况主要模拟运输车在满载情况下通过凹凸路面，后轮悬空时车架受力情况。以右后轮悬空为例，约束右前轮、左前轮全部自由度，约束左后轮y平动方向，释放左后轮其余自由度，右后轮释放全部自由度。车架扭转工况位移云图、应力云图如图5所示。

由图5a）可知：车架最大位移发生在车架右侧纵边梁和第7、8横梁处，为4.319 mm；右侧纵边梁位移由后向前逐渐变小，均小于3.359 mm，满足设计要求。原因是右后轮悬空时，车身总质量使右后车架翘曲变形。

由图5b）可知：最大应力在中间2个纵梁和第3横梁交叉连接处，为245.6 MPa。原因是右后车轮处于悬空状态，车架上方货物出现向左前侧倾覆性，货物载荷均由中间2个纵梁和第3横梁交叉连接处承受，扭转工况安全因数为1.40，不满足设计要求。

2.3 转弯工况

转弯工况指车辆在满载状况下转弯的工况，转弯时由于向心加速度作用，车架上各零部件的离心力载荷显著增加。以车架右转弯时为例，车架向心加速度约为0.23g（g为自由落体加速度），计算相应载荷后加载至z轴方向，约束情况和弯曲工况相同。车架转弯工况位移云图、应力云图如图6所示。

由图6a）可知：车架最大位移为车架左前和右前处，为5.958 mm。原因為货物重心在车架中心往后位置，右转时造成前端纵梁发生位移。

由图6b）可知：最大应力在中间2个纵梁和第3横梁、第6横梁交叉连接处，为289.9 MPa。原因为转弯时货物及支架产生的离心力载荷与重力载荷使支架与车架连接处产生更大的集中应力，转弯工况安全因数为1.19，不满足设计要求，存在安全隐患。

2.4 制动工况

制动工况指车辆在满载状况下紧急制动的工况，纵向惯性加速度使车架载荷发生变化，由于车辆一般在干燥沥青路面上行驶，将制动减速度设为0.6g，计算相应载荷后加载至z轴方向。约束右前轮、左前轮x、y、z平动方向，释放x、y、z转动方向；约束右后轮、左后轮x、y平动方向，释放x、y、z转动方向。车架制动工况位移云图、应力云图如图7所示。

由图7a）可知：车架最大位移在车架右后尾处，为2.486 mm。原因是前桥和车架连接处以中心支点连接，车辆紧急制动产生了纵向惯性力，导致车架右后翘曲，但翘曲为2.487 mm，满足最大变形不超过10 mm的安全设计要求。

由图7b）可知：最大应力在前桥与车架连接处，为198.4 MPa；原因是车架在纵向力作用下，车桥车架连接位置所受应力较集中，制动工况安全因数为1.74，满足设计要求。

经以上分析可知：转弯工况、扭转工况安全因数均较低，不符合设计要求，车架薄弱位置分别在中间纵梁和第6横梁连接处、中间纵梁和第3横梁连接处。

3 优化设计

优化车架结构薄弱处，把中间2个纵梁的槽钢厚度由6.0 mm增加至6.5 mm，第3横梁和第6横梁槽钢厚度由6.0 mm增加至7.0 mm，并在第3横梁与纵梁交叉处、第6横梁与纵梁交叉处增加厚、长、宽、高分别为10.0、108.0、102.0、140.0 mm的加强筋，优化后的车架示意如图8所示。

3.1 扭转工况

对优化后车架的扭转工况进行静力学分析，施加与2.2节相同的载荷和约束，优化后车架扭转工况位移云图、应力云图如图9所示。

由图9可知：车架最大位移由4.319 mm减小为3.027 mm，最大应力由245.6 MPa减小为196.4 MPa，安全因数为1.75，最大应力位置与优化前基本一致，为中间2个纵梁和第3横梁交叉连接处，优化后车架扭转工况安全因数满足强度要求。

3.2 转弯工况

对优化后车架转弯工况进行静力学分析，施加与2.3相同的载荷和约束，优化后转弯工况位移云图、应力云图如图10所示。

由图10可知：车架最大位移由5.958 mm减小为5.083 mm，最大应力由289.9 MPa减小为170.3 MPa，安全因数为2.02，最大应力位置与优化前基本一致，优化后车架转弯工况结构满足强度要求。

3.3 模态分析

AGV运输车在行驶时，来自路面、传动轴以及轮胎的不平衡造成运输车振动，振动频率约为15 Hz。为避免使用过程中出现共振，对车架进行模态分析，车架前6阶模态固有频率接近0，表明结构基本没有产生变形；车架7～12阶模态固有频率分别为21.342、63.137、81.690、103.569、112.790、137.936 Hz。从第7阶开始，模态固有频率不为0，最小模态固有频率为21.342 Hz，大于运输车振动频率，车架在正常行驶下不会发生共振。

4 结论

本文中针对AGV车架应力集中问题，构建车架有限元仿真模型，分析典型工况下最大应力发生的位置及原因，进行仿真优化并验证。

1）扭转工况和转弯工况的安全因数不符合设计要求，车架薄弱部位主要位于中间纵梁和第6横梁连接处、中间纵梁和第3横梁连接处。

2）增大中间纵梁、第3横梁、第6横梁的槽钢厚度，并在第3横梁与纵梁交叉处、第6横梁与纵梁交叉处设置加强筋，使车架扭转工况最大应力由245.6 MPa减小为196.4 MPa，转弯工况最大应力从289.9 MPa减小为170.3 MPa，车架结构优化后的2种工况安全因数均满足设计要求。

3）对优化后的车架进行模态分析，最小固有频率为21.342 Hz，避开了运输车的振动频率（15 Hz），有效避免低频共振的发生。

参考文献：

［1］ 韩自翔.自动导引运输车的开发与实际应用[D].北京：北京工业大学，2020.

[2] 张辰贝西，黄志球.自动导航车（AGV）发展综述[J].中国制造业信息化，2010，39（1）：53-59.

[3] 田会方，谭树栋，吴迎峰.基于EKF多传感器融合的自动导航车（AGV）位姿估计[J].电脑知识与技术，2022，18（20）：111-114.

[4] 石凯飞.真实路面激励下拖车车架瞬态动力学分析[J].农业装备与车辆工程，2023，61（8）：130-134.

[5] 王善军，余其霞.农用车底盘车架有限元分析[J].湖南农机，2010，37（9）：55-57.

[6] KIM H S，HUH H. Vechicle structure collapse analysis using a finite element limits method[J].Korea Advanced Inst of Science and Technology，1999（21）：436-499.

[7] 银俊鹰.某矿用自卸车车架强度有限元分析[D].呼和浩特：内蒙古科技大学，2014.

[8] 刘伦伦，张瑞亮，申晋宪，等．某主副一体式自卸车车架强度特性分析[J].机械设计，2015（2）：12-16.

[9] 吴磊.某隧道清筛车车架有限元静强度计算分析[J].工程技术研究，2023，8（5）：17-19.

[10] 王伟，王孟琴.某轻型卡车车架有限元分析[J].农业装备与车辆工程，2022，60（3）：156-160.

[11] 魏文涛，周盼.中型自卸车主车架设计与静力學分析[J].农业装备与车辆工程，2021，59（6）：130-134.

[12] 傅杰.某山地履带运输车车架的拓扑优化研究[D].重庆：重庆三峡学院，2023.

[13] 任宇刚.高强度结构钢在大型起重机臂架上的应用研究[J].中国重型装备，2023（2）：40-44.

[14] 赵强，刘丹丹，李旭，等.基于CAE技术的工程自卸车车架有限元分析[J].重型汽车，2022（5）：29-30.

[15] 李强.某重型载货车车架有限元静态及其试验研究[D].合肥：合肥工业大学，2009.

[16] 张忠元，张凤丽，郭军军，等.基于轻量化设计的空气冷却器支架有限元静动态分析[J].内燃机与动力装置，2021，38（1）：32-38.

[17] 张歆伊，郑再象，张友宏.基于Hyperworks的客车车架有限元分析[J].南方农机，2021，52（9）：16-18.

[18] 刘惟信.汽车设计[M].北京：清华大学出版社，2001.

[19] 中华人民共和国住房和城乡建设部.建筑机械使用安全技术规程：JGJ 33—2012[S].北京：中国建筑工业出版社，2012.

[20] 王涛.重型载货汽车车架有限元分析及优化设计[D].大连：大连交通大学，2020.

[21] 耿磊，唐公明，王敏，等.某混凝土搅拌运输车车架横梁的优化改进[J].汽车零部件，2023（5）：81-85.

Finite element analysis of AGV frame and its optimization

HU Zhongyi， HUANG Xuetao*， XU Yongchao， LIU Zihao， WANG Xiancheng

Automotive Engineering College，Shandong Jiaotong University， Jinan 250357，China

Abstract：In order to solve the problem of cracks in the frame of an automated guided vehicle （AGV） during use， a finite element model of the frame is established based on Solidwork. Hypermesh is used to conduct static analysis of the bending， torsion， turning， and braking conditions of the frame， identifying dangerous conditions and stress concentration areas. The thickness of the channel steel in the middle longitudinal beam， 3rd crossbeam， and 6th crossbeam of the frame is increased， and the thickness of the channel steel in the 3rd crossbeam install reinforcing ribs at the intersection of the 6th crossbeam and longitudinal beam， and conduct static and modal analysis on the optimized torsion and turning conditions of the frame. The results show that the maximum stress in the torsion and turning conditions of the optimized frame has been reduced， and the safety factor meets the design requirements; After optimization， the frame will not experience low-frequency resonance， solving the problem of frame cracks.

Keywords：AGV frame; finite element analysis; static analysis; modal analysis

（责任编辑：胡晓燕）

收稿日期：2023-07-31

基本项目：国家重点研发计划项目（301051103）

第一作者简介：胡忠义（1989—），男，山东枣庄人，硕士研究生，主要研究方向为有限元仿真技术，E-mail：419635052@qq.com

*通信作者简介：黄雪涛（1978—），男，山东东明人，博士，副教授，主要研究方向为有限元仿真技术，E-mail：xuetaohuang@163.com。