函数不等式的几种放缩法
2023-12-08 10:47陈彦男何红梅
数理化解题研究 2023年31期
肖 刚 陈彦男 何红梅 马 杰
(1.宜宾学院理学部,四川 宜宾 644000;2.宜宾三中,四川 宜宾 644000;3.简阳中学,四川 宜宾 641499)
文章通过将数列不等式视为函数不等式,通过构造法、联想法等方法来证明不等式的成立.
1 巧用Sn构造放缩函数
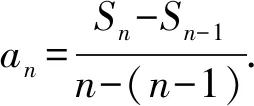
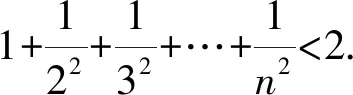
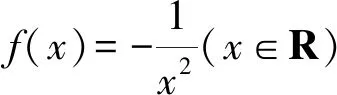
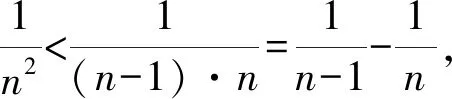
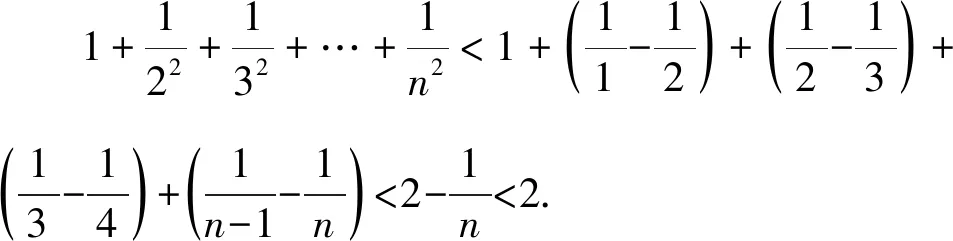
通过上述方法,我们很容易处理在自主招生和强基计划中出现过的类似数列不等式问题,例如复旦自主招生试题和上海交大自主招生试题.
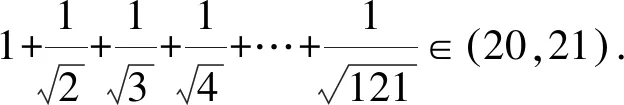
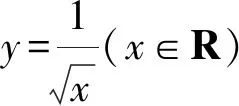
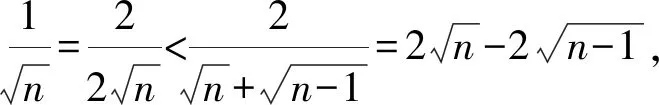
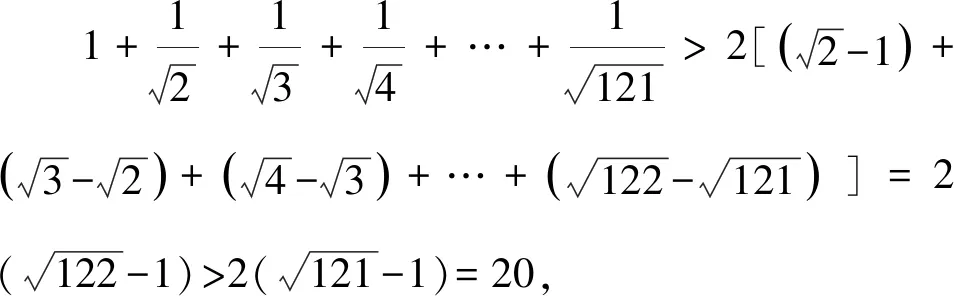
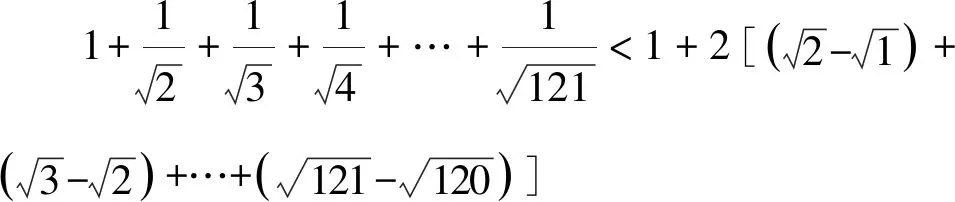
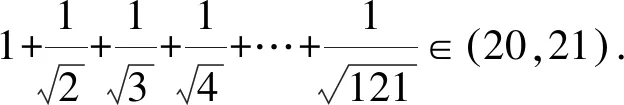
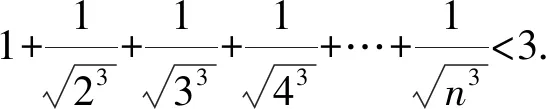
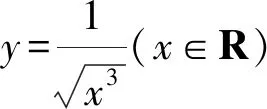
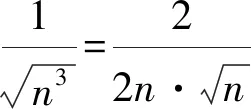
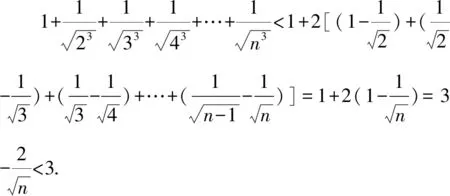
2 善用联想法构造新数列
对于常见的数列不等式,通常证明其小于或大于一个常数.此时,可以将常数联想成常见的数列[2].将数列不等式的证明转换成两个通项式的证明.例如卓越联盟自主招生考试的压轴题.
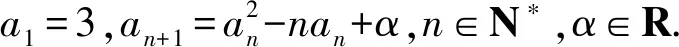
(1)若对∀n∈N+,an≥2n成立,求α的取值范围.
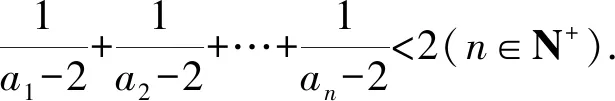
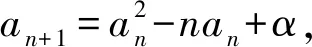
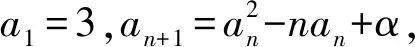
即需要证明:(1)an-2>(n-1)·n或(2)an-2>2n-1,对于(1)式,通过代入特例a1=3,a2=4,a3=6,a4=16,…,很容易否定(1)式不成立.而(2)式代入特殊项均成立.因此,需要证明an-2>2n-1,此式用数学归纳法即可证明.此题只给出第(2)问的详细解答过程.
证明(2)当n=1时,a1-2≥21-1,即a1≥20+2成立;
假设当n=k时,ak-2≥2k-1,即ak≥2k-1+2成立;
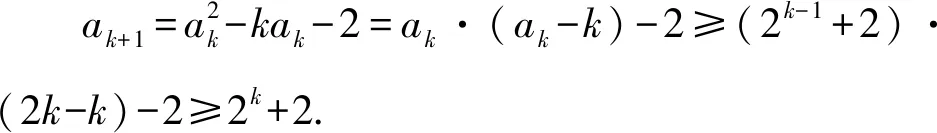
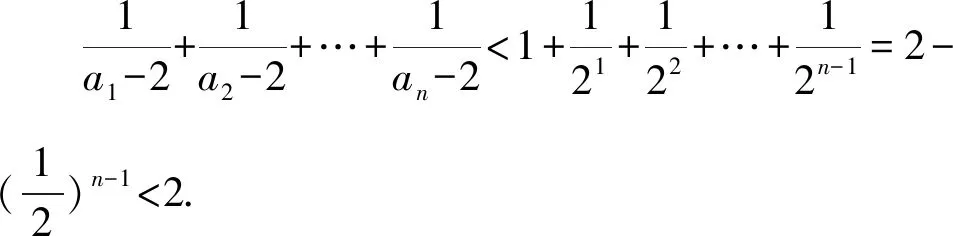
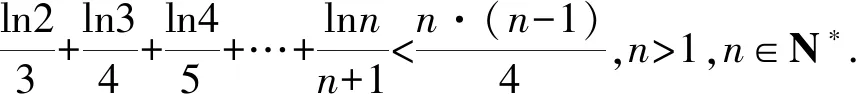
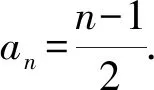
猜你喜欢
数学年刊A辑(中文版)(2021年1期)2021-06-09
文艺生活·中旬刊(2020年12期)2020-04-08
四川省干部函授学院学报(2019年1期)2019-06-25
成功(2018年11期)2018-12-28
新教育时代·教师版(2017年31期)2017-07-25
岷峨诗稿(2017年4期)2017-04-20
中国调味品(2017年2期)2017-03-20
山西大同大学学报(自然科学版)(2016年4期)2016-11-27
新高考·高一物理(2016年3期)2016-05-18
人民周刊(2016年4期)2016-02-29

