深度学习在元素测井中的应用

葛云龙，岳爱忠，宋森，张磊，骆庆锋，何绪新

（1.中国石油集团测井有限公司测井技术研究院，陕西 西安 710077；2.中国石油天然气集团有限公司测井技术试验基地，陕西 西安 710077；3.中国石油集团测井有限公司西南分公司，重庆 409912）

0 引 言

元素测井是储层评价中重要测井方法之一，它可以评价复杂地层的岩性，研究沉积环境、确定储层中矿物类型及含量[1-4]。目前，元素测井仪器理论研究和研制等方面均取得了明显的进展，复杂的地层矿物组成和井眼环境对元素相对产额的影响也得到了校正，元素测井已经被广泛应用到油气资源的勘探和开发中[5-7]。但是，对于小尺寸的测井仪器，由于探测器尺寸太小，导致探测效率降低，难以得到高精度的地层混合谱。另外，由于目前的能谱解析方法有限，计算的元素干重准确度不高。

深度学习是在机器学习的基础上发展起来的，它可以像人脑一样识别文字、图片和声音以及处理数据。深度学习主要是通过不断对地层的特征进行组合形成更高级的特征属性，来达到识别分析数据的目的[8-10]。利用深度学习方法，建立深度神经网络模型，使其对大量的元素测井混合谱与元素理论干重以及组成地层各矿物含量进行学习，得到元素测井混合谱和元素干重及矿物含量之间的关系模型，从而精确地计算元素干重和矿物含量。本文基于蒙特卡罗方法，采用深度学习的方法求解元素混合谱得到元素干重和矿物含量，通过不断改进方法、提高计算精度，为元素测井智能化应用提供理论基础。

1 计算模型

小型化的元素测井仪蒙特卡罗模型如图1所示，仪器外壳材料为钛合金，仪器直径为5 cm。中子源为脉冲中子源，能够放射14 MeV的单能快中子，保证快中子和地层产生非弹反应和俘获反应。仪器小型化是目前深地深海测井仪器研发的趋势，因此，探测器采用直径26.6 mm、长38 mm的圆柱形溴化镧晶体。溴化镧晶体作为探测器具有高探测器效率、良好高温特性等特点，同时有更高的计数率和较好的地层响应灵敏度，其源距为380 mm。在仪器的外表面，探测器外侧装有长29 cm、厚3 cm的硼套。为了防止中子源产生的中子直接进入仪器探测器影响探测结果，在中子源和探测器之间装一个直径为32 mm的屏蔽体，其材料为钨镍合金。

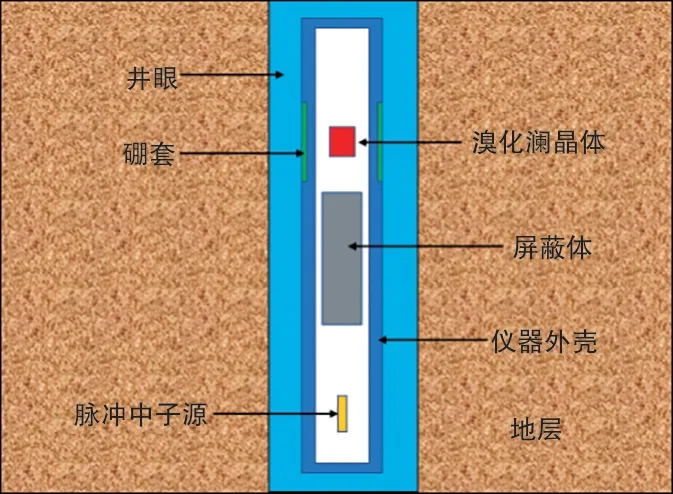
图1 计算模型

2 深度学习模型

全神经网络（Deep Neural Networks，DNN）是一个多隐层前馈神经网络，相邻层之间通过前馈权矩阵连接。利用DNN建立了地层混合中子伽马能谱与元素干重的关系模型，以及元素干重与矿物含量的关系模型。假设神经网络共有L层，第l层有N个神经元，输入数据为Zl-1，Zl-1为l-1层的输出。l层的输出为

式中，Wl为l-1层到l层的权重矩阵；bl为l层的偏差向量；fl为l层的激活函数。以整流线性单元Relu函数为激活函数，参数θ设为θ=｛Wl,bl|l= 1, 2, ∙∙∙,L｝，训练样本为x。训练损失函数E(θ，x)为

3 基于深度学习的元素测井解谱

3.1 样本处理

深度神经网络要经过大量样本数据的训练才能达到比较高的准确度，所以样本的数量和质量至关重要。一般用于训练的样本数量都比较庞大，难以通过实验或者模拟得到，需要利用随机数的方式合成大量样本数据。对于求解元素测井的中子伽马能谱来说，用于训练的样本是大量的混合谱和与之对应的元素干重，以及组成地层的矿物含量。无论是实际测井还是用蒙特卡罗数值模拟，获得上万个地层混合谱都需要花费大量的时间和资源，人为创造出与实际混合谱相符的数据就容易很多。地层混合谱是各元素标准谱贡献的总和，而每种元素贡献的份额可以用元素产额表示，元素产额与元素干重之间的关系为

式中，D为探测器对某元素的灵敏度，称为灵敏度因子，一般设Si元素的灵敏度因子为1，其他元素的灵敏度因子以Si元素为参照得到相对灵敏度因子；F为深度归一化因子；M为某元素在地层中的干重，%；y为某元素的产额，%。

根据地层信息确定元素种类，随机生成50 000组维数为元素种类数k、和为1的向量，即为元素产额的样本。将50 000×k的随机数组与元素标准谱矩阵k×256相乘，得到一个50 000×256的矩阵，并加入随机噪音，即为50 000个混合谱，将其作为输入样本。再由式 （4）将元素产额样本转换为对应的元素干重，作为输出样本。将输入样本和输出样本放进深度神经网络训练，并根据情况调整相关参数，建立学习模型。

3.2 解谱分析

理论上输入样本和输出样本都是实际情况得到的混合谱和元素干重，无论是非弹谱还是俘获谱都是可以直接通过深度神经网络训练直接应用的。对于人为制造的样本，所生成的是元素产额和各元素标准谱按产额贡献比相加得到的混合谱。俘获元素产额可以直接通过式 （4）转换为对应的元素干重，而非弹元素产额不能直接转换成元素干重，需要架桥元素含量已知，所以本文深度学习数据处理不涉及解非弹谱。

（1）地层组分为H2O、SiO2、CaCO3和CaSO4的组合。用表1中物质组分填充地层，模拟得到地层混合谱，采用全谱加权最小二乘法（全谱）和深度学习的方法分别解谱，计算结果如图2所示。由图2可以看出此种组合元素种类比较少， 两种方法计算结果误差都不大。其中误差最大的是Ca元素含量较大时全谱俘获计算的Ca元素干重，最大绝对误差为0.05%。深度学习计算结果整体误差较小。

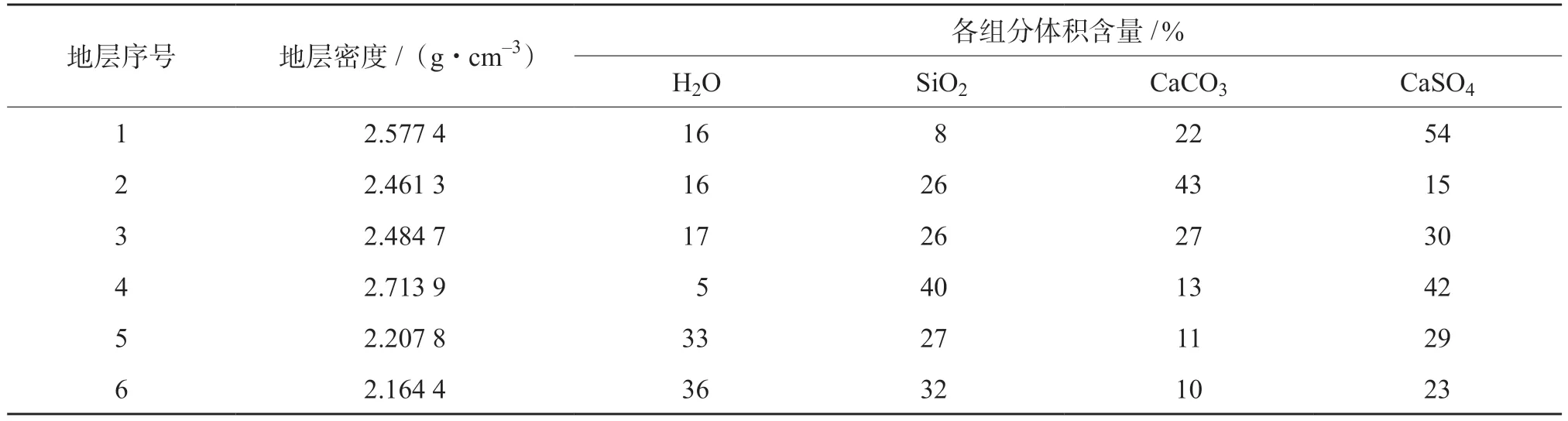
表1 地层各组分体积含量表（组合1）

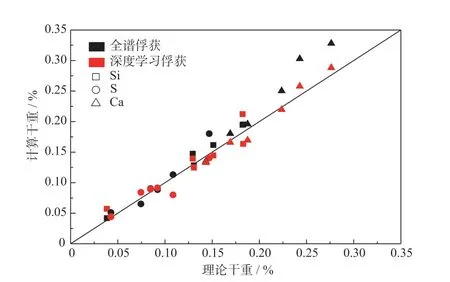
图2 解谱结果对比（组合1）

（2）地层组分为H2O、SiO2、CaSO4和CaMg（CO3）2的组合。用表2中物质组分填充地层，模拟得到地层混合谱，采用全谱加权最小二乘法和深度学习的方法解谱，计算结果如图3所示。

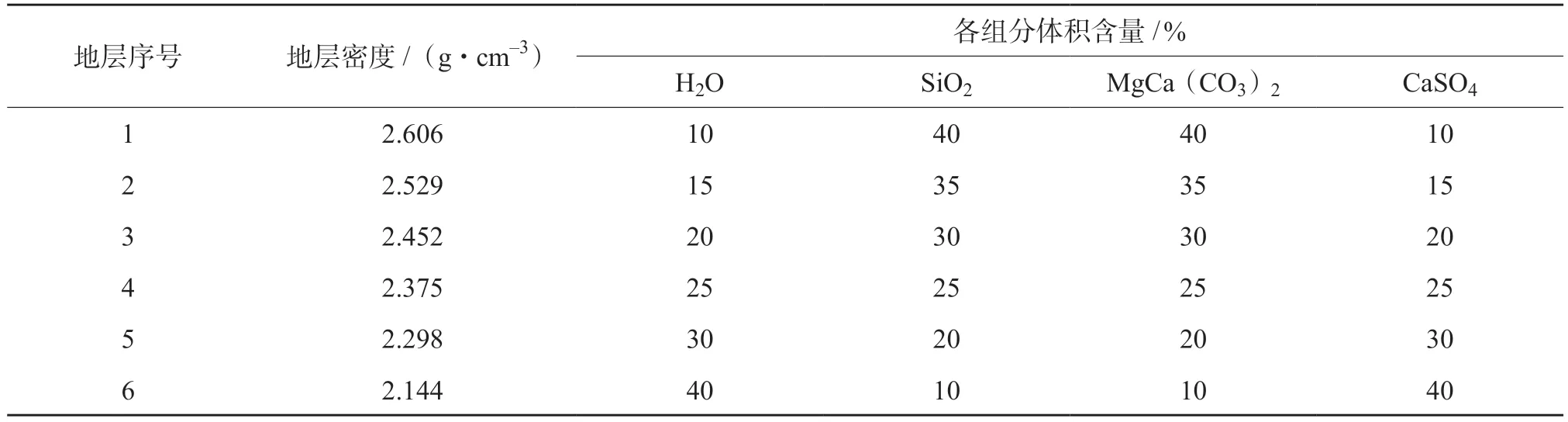
表2 地层各组分体积含量表（组合2）

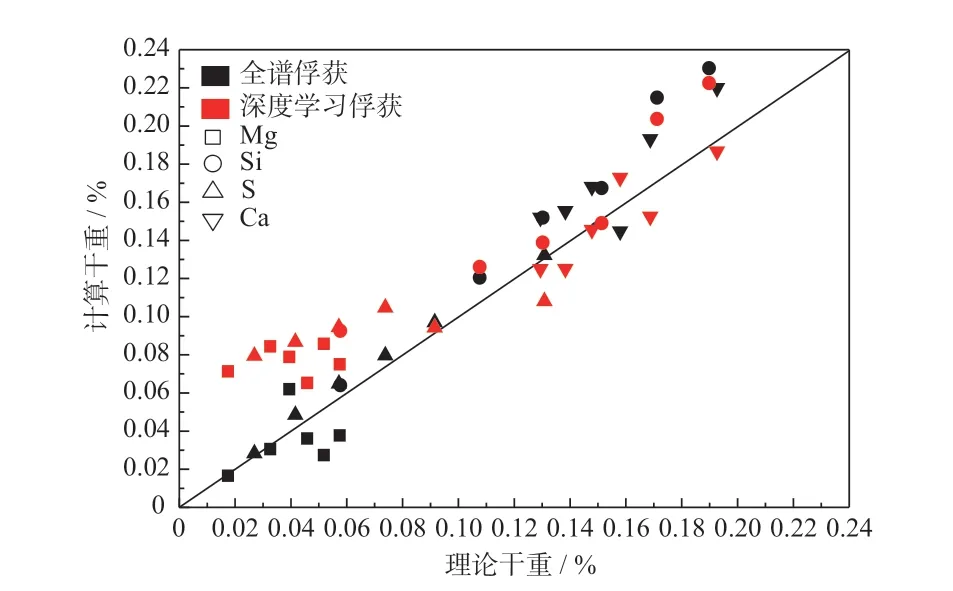
图3 解谱结果对比（组合2）

对比图2和图3发现，由于Mg元素的加入，全谱和深度学习计算误差都明显增大。深度学习方法对于灵敏度较低的元素，如Mg元素，其元素干重计算值偏大，对于灵敏度较高的元素，如Ca元素，其元素干重计算值偏小。

4 矿物含量计算

虽然自然界地层中含有的元素总类有上百种，但是 仅O、Si、Al、Fe、Ca、Na、K、Mg、H这9种 元素就占了所有元素总质量的98.13%。而且在目前已经查明的地层中虽然存在2 200多种矿物，但即便是矿物复杂的非常规地层组成的矿物也仅有十几种。一般情况下，组成矿物的元素的种类和含量是稳定的，这样就可选用一种或多种特征元素作为矿物的标志元素，如Si为石英的标志元素。利用俘获谱可以得到大多数常见元素的质量百分比，只有C和O元素不能通过俘获谱求出，只能通过非弹谱求出，而 Al、Ca、Fe、Mg、S、Si等元素既可以通过非弹谱求取，也可以通过俘获谱求取。如果已知地层元素的含量，就可以大致得到地层矿物的种类和含量。本文利用DNN神经网络建立了元素干重与岩石矿物含量的关系模型。对表3中数据进行计算，输入的元素干重为在理论干重中分别加入5%与10%不同程度噪声的干重。图4和图5分别为误差较小和较大时，深度学习法得到的矿物含量。可以看出，基于深度学习计算的矿物含量的精度取决于元素干重计算的准确性，当元素干重准确时，深度学习能准确地得到矿物含量。

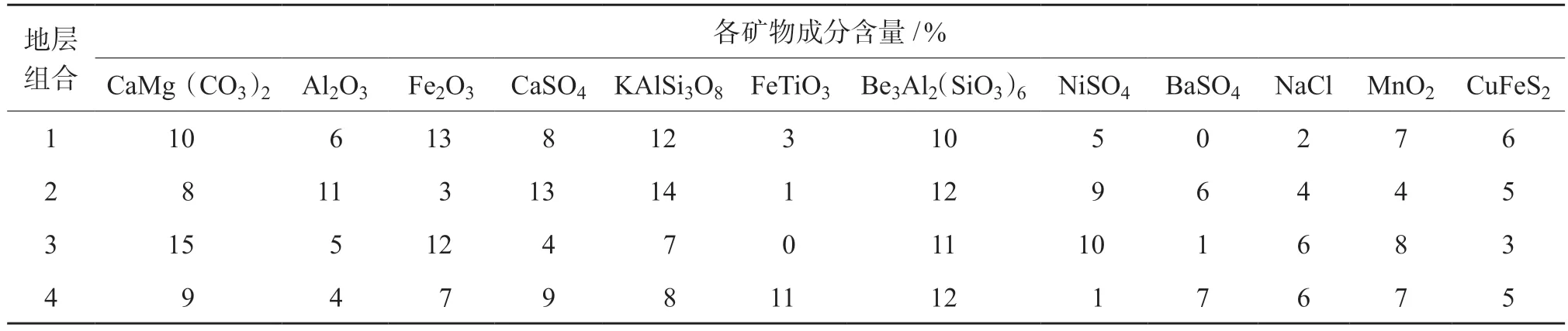
表3 矿物成分表

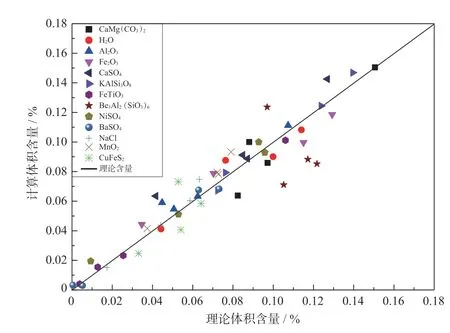
图4 误差较小时深度学习法计算结果

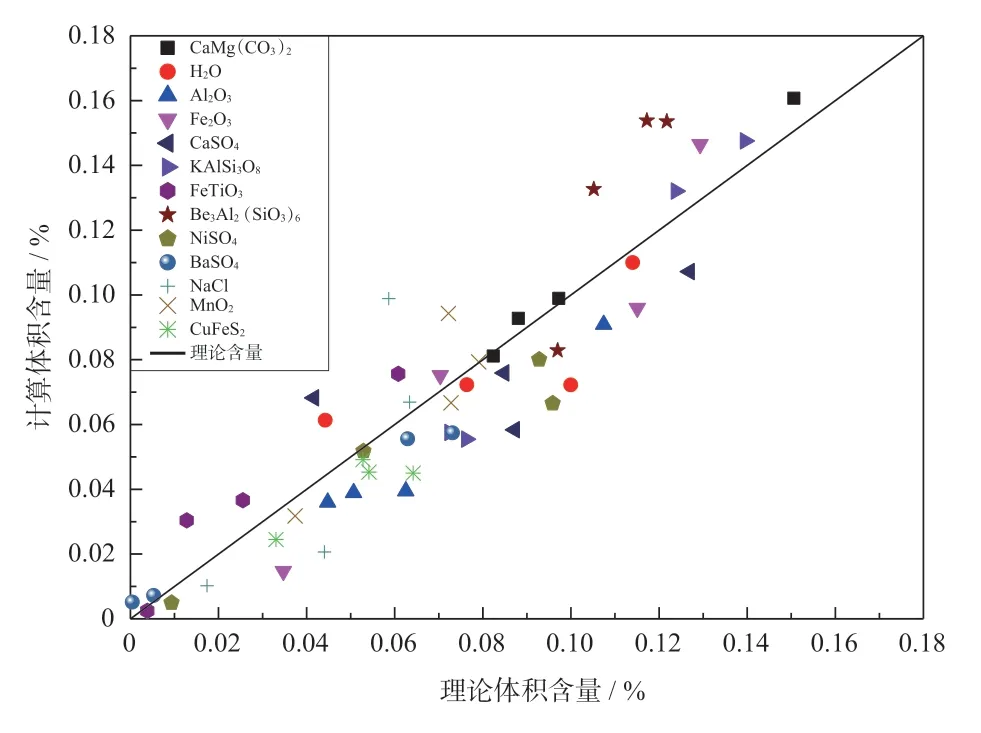
图5 误差较大时深度学习法计算结果

5 孔隙度计算

通过元素测井测量的地层伽马能谱和元素的标准伽马能谱，可以获得地层元素的产额。根据氧化物闭合模型，元素的产额可以转化为元素浓度。根据元素干重与岩石基质参数的关系，确定岩石基质参数，并结合常规孔隙度测井曲线计算地层孔隙度。声波测井对火成岩的岩性变化不敏感，当火成岩发生蚀变时，中子测井值会增加。因此，密度测井被用来计算地层孔隙度。基于体积物理模型，可以得到式 （5）。

式中，φ为地层孔隙度，p.u.；ρb为测量的密度，g/cm3；ρma为岩石骨架的密度，g/cm3；ρf为地层流体密度，g/cm3。深度学习直接建立元素干重与岩石基质密度之间的关系模型，通过输入元素浓度可以直接获得岩石基质密度。

测井实例是准噶尔盆地西北边缘的一口井，目标层为石炭系火成岩地层。该地区石炭系大部分处于海相和海陆沉积环境中，火成岩基底厚度大。元素捕获光谱测井（Element Capture Spectrum）用于测量地层的元素浓度。根据岩心分析数据，主要岩性为火成岩（安山岩、凝灰岩等）和泥岩，同时还分布有砂岩和砾岩。火成岩的裂缝更为发育，也有少量的孔洞。根据物性分析数据，孔隙度为1 ～20 p.u.，集中在5 ～15 p.u.，岩心密度集中在2.3 ～2.7 g/cm3。基于岩心分析数据，选择表1中的矿物来建立地层，元素浓度可以通过蒙特卡罗模拟的方法获得。基于深度学习建立了元素浓度与岩石基质密度之间的关系模型，可以获得岩石基质密度。地层孔隙度可以通过将岩石基质密度与密度测井相结合来获得（见图6），通过深度学习计算的孔隙度接近岩心孔隙度。

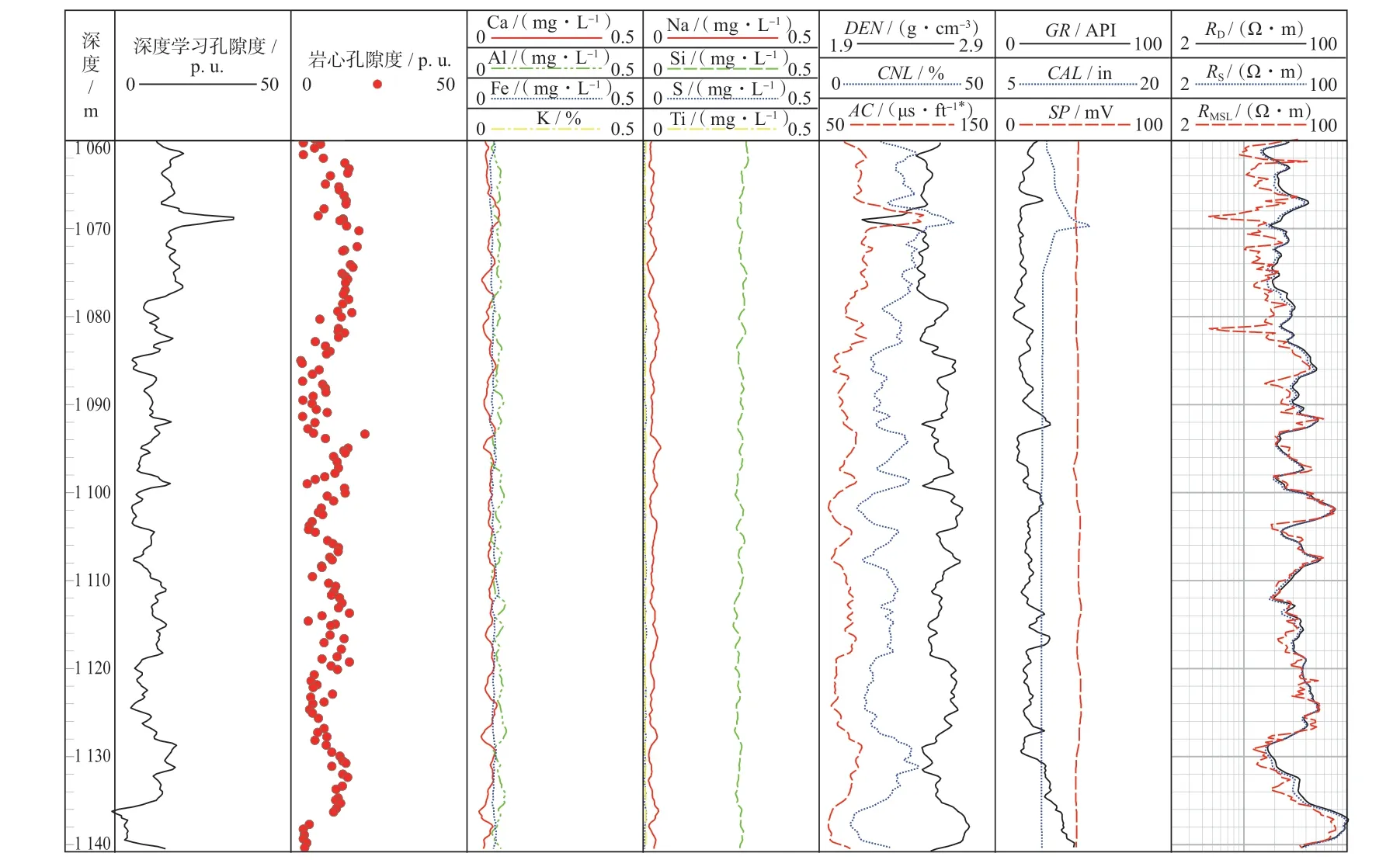
图6 基于深度学习孔隙度计算结果

6 结 论

（1）采用蒙特卡罗方法制作学习样本时，对于灵敏度较低的元素，如Mg元素，其元素干重计算值偏大，对于灵敏度较高的元素，如Ca元素，其元素干重计算值偏小。整体而言，当元素种类较少时，深度学习的解谱效果好于传统的全谱加权最小二乘法解谱，随着元素种类的增多，其计算误差增大。

（2）基于深度学习计算的矿物含量的精度取决于元素干重计算的准确性，当元素干重较为准确时，深度学习能较为准确地得到矿物含量。 深度学习可用于建立元素干重与岩石骨架参数之间的关系模型。例如火成岩地层，同一岩性的岩石基质参数可能不同。在利用常规测井资料计算孔隙度时，岩性分类是第一步，也是最重要的一步。当元素干重数据可用时，可通过元素干重获得岩石骨架密度，进而计算地层孔隙度，无需进行岩性分类。