2023年高考全国乙卷理综第25题(3)的改编和拓展
刘 鑫
(瑞金第一中学)
一、原题呈现与改编
(1)原题呈现


图1
(1)第一次碰撞后瞬间小球和圆盘的速度大小;
(2)在第一次碰撞到第二次碰撞之间,小球和圆盘间的最远距离;
(3)圆盘在管内运动过程中,小球与圆盘碰撞的次数。
(2)试题改编
第(3)问因涉及连续碰撞而难度陡增。这显然是为了确保顶尖名校选才所必需的区分度和服务科学选才量身打造的,对特尖生而言,它的重要性不言而喻。截至目前,关于原题解法的讨论已经很多了。前人之述备矣!为了得到更多、更详尽的信息,本文接下来仅针对第(3)问对原题进行改编。
情景、碰撞类型、质量关系和设问等均不变,只改一个条件——“圆盘滑动摩擦力与其所受重力大小相等(即Ff=Mg=3mg)”,更改为“Ff=kMg=3kmg”,即用一个无量纲的系数k对圆盘滑动摩擦力的大小做一般化的处理,再来求解第(3)问。
二、改编试题分析、解答和拓展
(1)改编试题分析
k取不同的值,薄圆盘的受力、运动情况将发生改变。可以采取先易后难、逐个击破的策略,把k分区间,然后逐一去讨论、研究。同时,转换参考系可以迅速地得出一些重要结论;研究系统质心运动可以避开逐次处理各次碰撞的烦琐运算。这些都将在很大程度上简化解答,便于得出碰撞次数n与k的关系。
(2)改编试题解答


管内不发生碰撞,因此碰撞次数n=0。证明较易,从略。

选择竖直向下为正方向(此后不再赘述)。对薄圆盘,由牛顿第二定律有
a=(1-k)g
(1)
第一次碰撞时

发生第一次碰撞前瞬间,小球和薄圆盘的速度分别为
以薄圆盘为参考系,因它除碰撞瞬间外均向下做匀加速直线运动,所以是非惯性参考系,牛顿运动定律经修正后方可使用。相对薄圆盘,除碰撞瞬间外,小球均做加速度为(g-a)的匀变速直线运动。同时,碰撞均为弹性碰撞(即恢复系数为“1”,两者碰前瞬间的接近速度等于碰后瞬间的分离速度),结合竖直上抛运动的对称性,从第一次开始推算,发现每次碰撞前小球总是以v0撞下来,碰撞后它又以v0反弹上去。因此,任意相邻两次碰撞的时间间隔恒为
以小球释放瞬间作为计时起点,以圆管的上端口作为坐标原点,由质心的定义,系统质心初始位置
因合外力恒定,系统质心向下做初速度为零、加速度为ac的匀加速直线运动
4mg-3kmg=4mac
值得指出的是,ac并不受碰撞内力的影响。在M冲出圆管前,发生第n次碰撞时(薄圆盘、小球以及系统质心三者重合),运动时间和质心位移分别为
临界条件满足如下关系


(11)


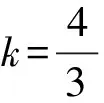
参照②的分析,任意相邻两次碰撞的时间间隔恒为
考虑到薄圆盘摩擦力的突变,为方便计算,把薄圆盘的初始位置作为坐标原点,把小球与薄圆盘首次碰撞的瞬间作为计时起点。接下来具体的做法同②。这里直接给出结果。

(16)
经过分子有理化

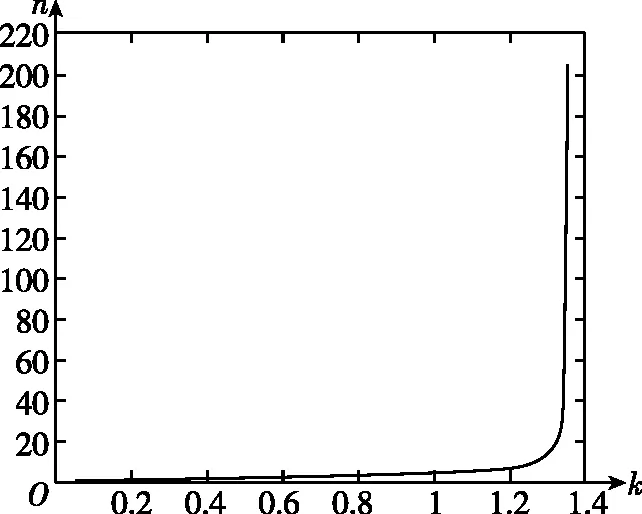
4.89 由前面的讨论可知,薄圆盘不会自发地下滑,而且在第二次碰撞之前已停下可被小球撞击。从第一次碰后开始到第二次碰撞前,薄圆盘向下运动的时间和位移分别为 设小球第二次与薄圆盘前碰的速度为vt则有 由相遇条件(位移相等) 整理上式可得 整理得 同理,小球再次碰撞薄圆盘时,薄圆盘第二段位移 因此,两段位移之比 而a=(1-k)g,代入(26)式得 值得一提的是:如果第二次碰前薄圆盘已停下。那么,此后每次均是如此。这个结论可以用归纳法来证明。即证明:假设第k次碰后分开,第k+1次碰前薄圆盘已停下。那么,第k+1次碰后分开,第k+2次碰前薄圆盘已停下。设第k+1次碰前(按假设薄圆盘已停下),小球向下的速度为vk;第k+2次碰前小球向下(对地)的速度为vk+1。第k+1次碰后薄圆盘向下运动的时间(按假设,第k+1次碰撞属“一动碰一静”模型,借鉴原题第一问,计算较简单,此处略) 对小球 薄圆盘相邻两次的位移之比q为与具体的速度无关的定值,所以薄圆盘每次向下滑行距离yi是等比数列,求和 (32) (3)改编试题拓展 为了检验理论分析的正确性,笔者还借助matlab软件,画出了碰撞次数n与k的分段函数图像,如图2。图像显示的规律与本文的理论研究吻合得相当之好,证明本文的理论分析完全正确。 图2


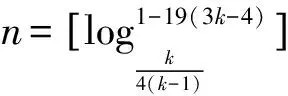



三、软件系统仿真
四、总结和展望


——兼谈参考系与坐标系的关联关系

