塑料排水板处理近海软土地基的沉降量分析
贺炜,胡彬,王晓佳,尹平保
(1. 长沙理工大学 土木工程学院,湖南 长沙 410114;2. 保利长大工程有限公司,广东 广州 511430)
软土地基的沉降分析一直是岩土工程中的重难点问题[1-5]。为避免在荷载作用下软土地基产生过量的工后沉降,采用塑料排水板对软土地基进行预压是一种广泛使用的有效方法。由于软土的复杂性和不确定性,沉降量的理论分析难以获得准确的结果。因此,对软土地基的沉降量进行数值模拟分析、监测数据对比和可靠性分析是非常有必要的。
目前,许多学者对塑料排水板预压处理软土地基进行了多方面的研究。朱森林[6]通过对潮汕机场大面积深厚软土的研究,发现采用塑料排水板作为竖向排水通道的堆载预压技术可以较好地解决沉降变形问题。刘爱民等[7]比较了整体式塑料排水板与普通塑料排水板的加固效果,发现在新吹填的淤泥和流泥等超软土地基中,前者由于适当提高了滤膜的等效孔径,加固效果更好。黄建华等[8]对经过塑料排水板堆载预压处理的某变电站软基进行分析,得出在考虑涂抹和井阻作用影响下的固结度更符合实际情况的结论。谢非等[9]进行堆载预压塑料排水板软基处理研究时,利用监测数据,科学合理地指导了施工。李少和等[10]通过对某四面环海工程的软基进行实测和理论计算预测,得出了在饱和黏土中主要发生主、次固结沉降的结论。黄朝煊等[11]基于等应变假设,类比于砂井地基固结理论,推导了排水板地基固结的解析解,并通过有限元软件验证了其合理性。张甲峰等[12]采用有限元分析软件与监测数据对比,发现利用塑料排水板对超大面积深厚软基进行堆载处理时,有必要考虑沉降中的软土蠕变。董超强等[13]针对某超软土地基,分别采用有限元软件中的排水线模型和Chai简化模型对塑料排水板进行模拟计算,并与监测数据进行比较,验证了等效系数方法的可靠性。在预测工后沉降方面,多以结合监测数据的方法为主,如浅岗法、Asaoka 法、双曲线法、三点法、星野法和指数曲线法等。
在固结沉降的分析中,采用有限元模拟和监测对比,还应考虑土体参数的不确定性对预测工后沉降的影响,但实际工程中考虑这种影响的研究鲜见,有必要深入开展研究。本研究以深中通道伶仃洋大桥西锚碇人工岛软基处理为工程背景,拟利用有限元软件对施工期的固结沉降进行模拟分析,并与监测数据作对比,分析塑料排水板预压对沉降的影响。在考虑土体参数具有不确定性的基础上,分析渗透率对工后沉降预测的影响程度,得到的结论可为类似工程提供相关经验。
1 工程概况
深中通道(深圳至中山跨江通道)伶仃洋大桥西锚碇人工岛位于伶仃洋上。该区域的土体主要由淤泥、粉质黏土、粗砂、淤泥质粉质黏土和风化花岗岩组成。
在进行西锚碇施工之前,需要修筑人工岛来避免水下施工。其步骤如下:
1) 采用深层水泥搅拌(deep cement mix,DCM)桩和土工管袋围堰形成外沿岛体。
2) 在岛体内部打设塑料排水板,吹填厚约5.6 m的中粗砂,形成整个岛体。
吹填的中粗砂不仅起到水平垫层的作用,还可以作为预压荷载(约为121.5 kPa)。
西锚碇人工岛岛体结构及地基处理的情况如图1所示。

图1 人工岛岛体结构及地基处理示意Fig. 1 Illustration of island structure and foundation treatment
2 人工岛固结沉降理论和数值模拟
2.1 塑料排水板处理软基固结沉降计算理论
塑料排水板预压已经作为一种成熟的软基处理方法,被广泛运用于各种大型工程建设中[14-16]。它通过缩短渗透性低的软基的排水路径,并施加预压来加速土体固结,从而达到强度增长的目的。
典型的塑料排水板(prefabricated vertical drain,PVD)地基处理计算固结模型如图2 所示[11]。其中,L为塑料排水板的计算长度;b、δ分别为塑料排水板截面宽度和厚度;re为塑料排水板有效排水直径。在土体固结过程中,塑料排水板周围形成了一个半径为rs的涂抹区。固结度用式(1)计算[17]:
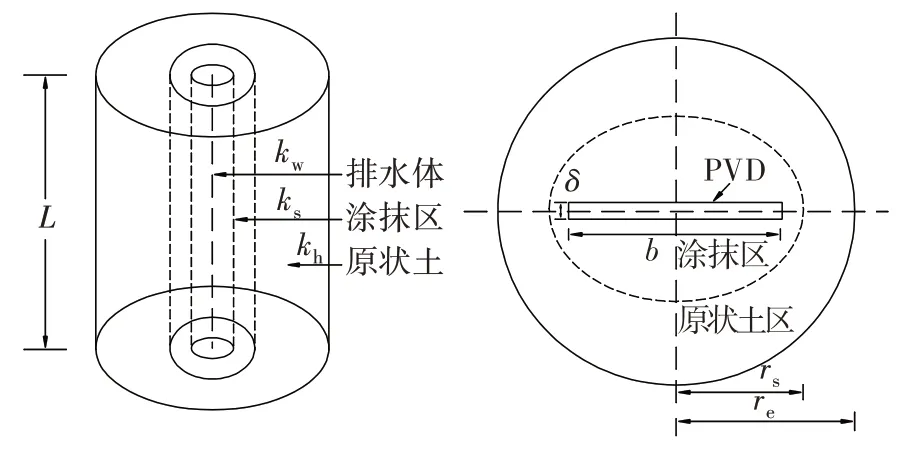
图2 PVD地基处理固结模型示意Fig. 2 Illustration of consolidation model of soil treated using PVD
式中:Ur为地基土径向固结度;
α、β为参数;
t为固结时间。
考虑井阻和涂抹效应,α取1,β由式(2)计算:
式中:de为塑料排水板有效排水直径2re;
Ch为土层水平向固结系数,可由式(7)计算;
Fn、Nw为参数,可由式(3)和(5)计算。
式中:n为井径比,等于de/dw。
dw为塑料排水板当量换算直径,由式(4)计算。
式中:b、δ取值见文献[18]。
式中:ks为涂抹区土的渗透率,取值见[19];
kh为土层水平向渗流系数;
s为涂抹区直径ds=2rs与dw之比,可取2.0~3.0;
kw为排水体渗透率。
其中,kw可由式(6)计算:
式中:qw为塑料排水板纵向通水量[17]。
式中:e为天然孔隙比;
a为压缩系数;
rw为水的重度。
当等边三角形排列时,de=1.05l;当正方形排列时,de=1.13l。其中,l为塑料排水板间距。
最终沉降量按式(8)计算[20]:
式中:Cc为压缩指数;
Ce为再压缩指数;
H为土层厚度;
ROC为超固结比(over-consolidation ratio,OCR);
pc为先期固结应力;
p为施加荷载后的有效应力;
e0为初始孔隙比,可通过e-lgp曲线获得。
工后沉降按照式(9)计算:
式中:St为施工完成时的沉降,St=S×Ur。
2.2 计算模型理论分析
针对塑料排水板预压地基的建模问题,有两种常用的处理方法:
1) 利用软件自带的排水单元进行塑料排水板模拟。如:使用Plaxis 软件中的排水线来模拟塑料排水板。
2) 利用等效原则来处理塑料排水板地基。如:运用砂井固结理论分析,将塑料排水板等效简化为砂墙模型,或根据固结度等效原则简化为天然地基[12-13,21-26]。
本研究以不规则的椭圆形人工岛为工程背景。在地基处理过程中,需要打入上万根塑料排水板。考虑到采用排水单元或砂墙进行三维模拟会降低计算效率。因此,利用固结度等效原则,运用砂井固结理论分析,将塑料排水板地基等效简化为竖向渗透率kve较大的天然地基[22-23],其计算式如下:
式中:kv为土层竖向渗透率;
h为每层土体塑料排水板打设深度。
在淤泥2-1、淤泥2-2 和粉质黏土2-22 的塑料排水板处理区域,μ值分别为2.506、2.653、5.132,将这些值代入式(10),可以算出塑料排水板处理区域的等效渗透率。各土层渗透率以及通过该理论计算出的塑料排水板处理区域的等效渗透率见表1。

表1 土层渗透率及等效渗透率Table 1 Soil permeability coefficient and equivalent permeability coefficient
2.3 计算模型建立及参数设置
采用Midas GTS 有限元软件对西锚碇人工岛进行模拟,整个人工岛模型呈不规则椭圆形。建模时,采用岩土工程领域广泛应用的摩尔-库伦本构模型。该模型的主要参数包括弹性模量E、泊松比ν、容重γ、黏聚力c和内摩擦角φ。根据深中通道伶仃航道桥工程的地质勘查报告,确定模型参数,见表2。人工岛模型如图3所示。其中,塑料排水板处理区域等效竖向渗透率见表1。

表2 土层参数设置表Table 2 Parameter setting table of soil layer and structure
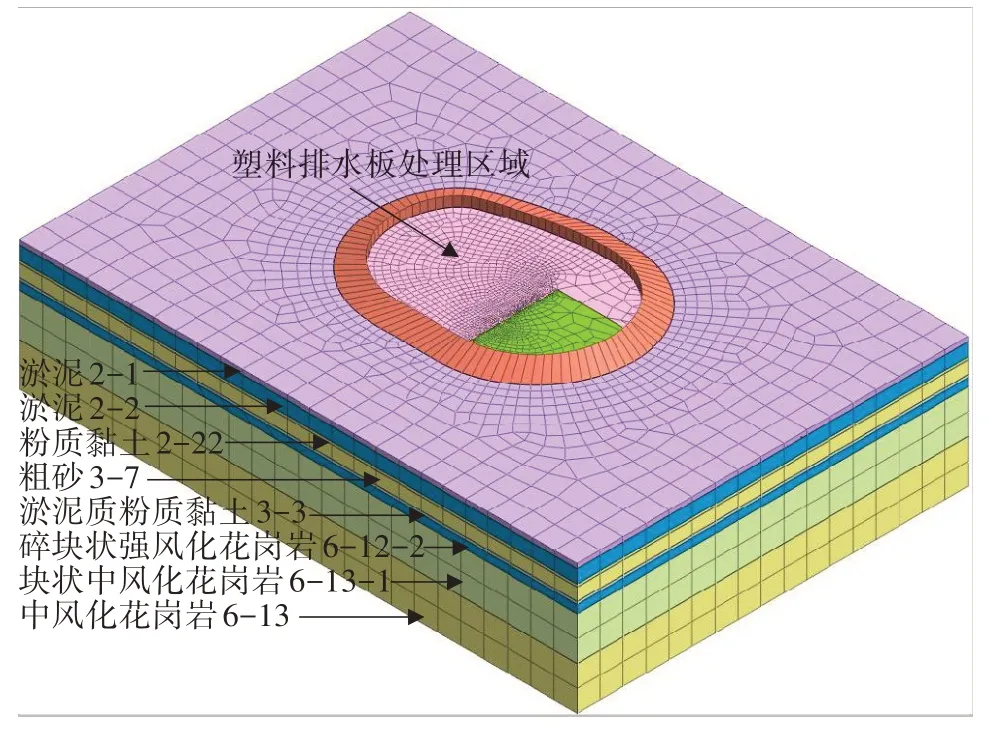
图3 人工岛模型示意Fig. 3 Artificial island model
模型计算工况与实际工程的吹填工况大致相同,具体的计算工况见表3。

表3 施工模拟步骤Table 3 Construction simulation steps
在进行固结沉降计算模拟时,主要模拟吹填预压期的沉降变化。因此,前4 道工序总共设置为1 d,吹填第一层工序设置为60 d,吹填第二层工序设置为40 d,空置期工序设置为200 d;再对塑料排水板堆载预压处理的软土地基固结沉降量进行研究。
2.4 数值模拟结果与监测结果对比
人工岛岛体内部塑料排水板的处理范围不包括拌和楼和料仓区。在人工岛布置了MDB2 和MDB3 两个观测点,监测人工岛塑料排水板处理范围的地表沉降情况,如图4 所示。地表沉降监测结果和模拟结果如图5所示。

图4 岛体平面示意Fig. 4 Plane schematic of the island
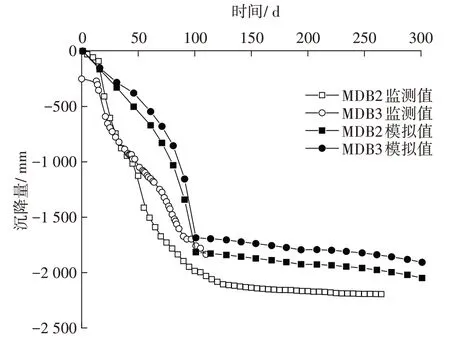
图5 地表沉降量监测与模拟值变化曲线Fig. 5 Surface subsidence monitoring and simulation curve
从图5可以看出,监测点MDB2和MDB3的地表沉降监测值与数值模拟得到的地表沉降量相近,且变化趋势相似。这表明数值模拟结果能够较好地反映实际工程中地表沉降的变化情况。从图5还可以看出,在打设塑料排水板后,吹填预压期的固结沉降发展较快,这表明在吹填预压作用下,塑料排水板效果明显,符合实际工程情况。然后,在吹填预压期,数值模拟曲线的沉降速率小于监测曲线的沉降速率,这可能是因为实际工程中加入了少许砂桩进行处理,加速了土体排水固结。
3 影响因素分析
3.1 影响因素分析方案
塑料排水板的打设间距和通水量影响软土地基的处理效果。为探讨这些因素对人工岛固结沉降的影响,在该工程的基础上,制定一个影响因素分析方案,并进行建模分析。分析方案见表4。在进行分析时,以某一因素(打设间距或通水量)作为变量,其他因素不变,而其他因素为弹性模量E、泊松比ν、容重γ、黏聚力c和内摩擦角φ。
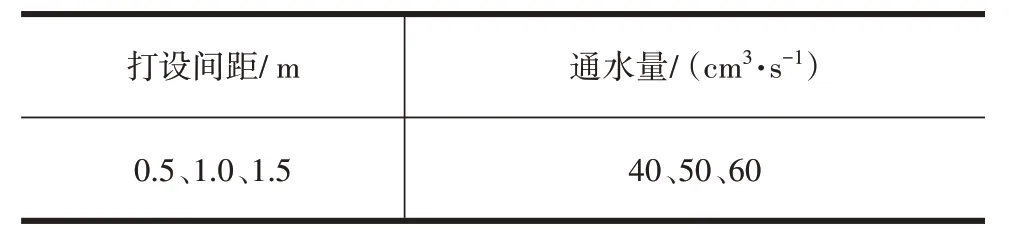
表4 固结沉降的影响因素Table 4 Scheme of parameters analysis
3.2 塑料排水板打设间距的影响
对塑料排水板设置不同的打设间距,并统计不同打设间距下岛体中部位置的地表沉降变化曲线,如图6所示。
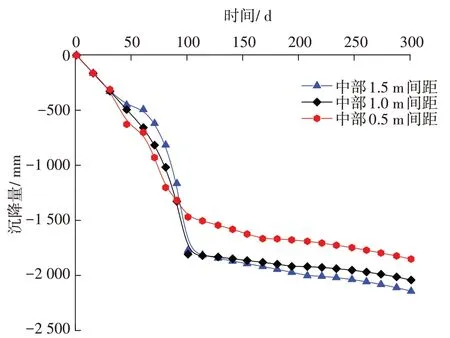
图6 不同打设间距下岛体中部地表沉降变化曲线Fig. 6 Variation curve of surface settlement in the middle of island under different spacing
从图6 可以看出,随着塑料排水板的间距逐渐减小,吹填预压期的沉降量逐渐增大,表明减小塑料排水板的间距会增大固结沉降量。当塑料排水板间距从1.5 m 减小至1.0 m 时,吹填预压期的沉降量差值大于塑料排水板间距由1.0 m减小至0.5 m的沉降量差值,表明当间距低于1.0 m 时,固结沉降量虽然变大,但固结沉降速率逐渐变小。当塑料排水板间距改变时,吹填预压期固结沉降量可相差300 mm以上,表明塑料排水板间距的改变对固结沉降速率的影响显著。从图6 还可以看出,最终固结沉降量的变化较稳定,但吹填结束后,塑料排水板间距为0.5 m 的最终沉降量发展较慢。这是因为排水板间距过密,可能对土层产生了较大扰动,影响后续的固结沉降。塑料排水板间距过大,会影响吹填预压期的固结速率;塑料排水板间距过小,可能会对土层产生较大扰动,影响吹填后的固结沉降。因此,在实际工程选择时,宜选择约1.0 m 的塑料排水板间距。
3.3 塑料排水板通水量的影响
塑料排水板通水量对人工岛体固结沉降的影响如图7所示。

图7 不同通水量下岛体中部地表沉降变化曲线Fig. 7 Variation curve of surface subsidence in the middle of island under different water flow
从图7 可以看出,随着塑料排水板通水量的增加,吹填预压期固结沉降量逐渐上升,表明在塑料排水板预压处理固结沉降中,增大通水量能提高固结速率。与通水量从50 cm3/ s 增大到60 cm3/ s 的固结速率相比,当通水量从40 cm3/ s 增大至50 cm3/ s时,固结速率增加显著,表明当通水量大于50 cm3/ s时,继续增大通水量,对提高固结速率的作用变小。在空置期,固结总沉降量并没有太大变化,表明塑料排水板通水量的增加对固结总沉降量的影响不显著。在不考虑材料造价的前提下,选择塑料排水板时通水量应越大越好,但也须根据具体工程实际情况综合考虑,本工程选择通水量为50 cm3/ s 的塑料排水板进行软土地基处理。
4 渗透率对预测工后沉降的影响
工后沉降是软土地基沉降量分析中的重点之一。在软土地基中,由于土体渗透率等土性参数存在不确定性,无论是数值模拟,还是理论计算,都无法准确量化土性参数对预测工后沉降的影响。因此,本研究结合固结沉降理论和蒙特卡洛法,利用编程软件探讨了渗透率的不确定性对预测工后沉降的影响程度。
根据伶仃航道桥工程地质勘查报告,淤泥2-1渗透率的平均值为0.72×10-6cm/s,淤泥2-2渗透率平均值为0.47×10-6cm/s。为了满足该实际工程,假设淤泥层渗透率的变化范围为0.40×10-6~0.80×10-6cm/ s。根据文献[27]和勘查报告统计出的淤泥层渗透率变异系数,将渗透率变异系数的取值范围设置为0.500 ~ 0.900。
当渗透率符合对数正态分布变化时,不同渗透率均值μk和相同渗透率的变异系数KCOV(coefficient of variation,COV)为0.7 时的工后沉降情况如图8 所示。理论计算出的工后沉降量(箭头指向的值)也叠加在图中,以便与工后沉降量直方图进行比较。


图8 不同渗透率均值下的工后沉降量直方图Fig. 8 Post-construction settlement histogram under different μk
从图8 可以看出,当渗透率符合对数正态分布时,工后沉降也近似服从对数正态分布。工后沉降在一个较大的范围内波动,多分布在工后沉降的右侧,这表明当μk大于0.50 时,会显著影响工后沉降的预测。
相同渗透率均值为0.5×10-6cm/ s 时,不同渗透率变异系数对工后沉降的影响如图9所示。

图9 不同渗透率变异系数下的工后沉降量直方图Fig. 9 Post-construction settlement histogram under different Kcov
从图9可以看出,随着渗透率的增大,工后沉降预测的范围逐渐增大,并且工后沉降的预测值逐渐向右偏移。这表明渗透率的变化对工后沉降的预测具有显著影响。
5 结论
以深中通道西锚碇人工岛为工程背景,采用数值模拟的方法,对岛体固结沉降进行模拟计算。通过影响因素分析和可靠性分析,得出以下结论:
1) 采用固结度等效原则的塑料排水板预压软土地基的数值模拟,是处理软土地基的数值模拟计算中的有效方法之一。既可以较好地模拟固结沉降,也可以避免塑料排水板数量过多使模型复杂化的问题。
2) 塑料排水板的间距和通水量均会影响软土地基固结沉降速率。塑料排水板间距越小,固结沉降速率越大,但对土层的扰动也会变大。因此,应根据实际工程选择适宜的排水间距。在无其他因素限制的情况下,宜选择通水量较大的塑料排水板,因为通水量越大,固结沉降速率越大。但改变塑料排水板的间距和通水量对最终的固结沉降量影响不大。
3) 运用Matlab GPT 计算固结沉降量,并假设渗透率符合对数正态分布。当μk变化范围为0.4×10-6~ 0.8×10-6cm/ s,Kcov变化范围为0.5~0.9 时,利用蒙特卡洛法模拟渗透率的变异系数分析对工后沉降的影响。计算结果表明,渗透率的变异系数分析对工后沉降的预测结果具有显著影响。

