静压支撑单点渐进成形厚向应变分布研究

尚苗，李言，赵兴百，杨明顺，陈匡禹

（西安理工大学 机械与精密仪器工程学院，西安 710048）

单点渐进板材成形（Single point incremental forming，SPIF）是一种快速、灵活的板材成形技术。通常使一个通用的工具头按照预定义的轨迹逐点累积成形，从而实现多种形状薄壁制件的数字化制造[1-2]。SPIF 技术不需要专用的模具或工具组，极大的缩短了产品交货时间、节约了生产成本，在产品定制、原型制造及多品种小批量生产中潜力巨大[3]。

在SPIF 单道次加工高成形角和复杂形状零件的过程中，厚度分布不均匀和局部过度减薄，易于引起板材的塌陷、失稳和过早破裂，严重影响了制件的几何精度、成形性能和成形质量，阻碍了SPIF 技术在航空航天、交通运输、医疗卫生、建筑设计等领域的大规模推广和使用[4]。

为了提升成形板材的厚度分布性能，学者们对SPIF 进行了大量研究。Cao 等[5]通过研制新型的渐进成形刀具，Wu 等[6]采用扁平椭圆形尖端的新型振动刀具，有效的促进了厚度分布，提高了制件的成形性能。周六如[7]采用平行直线型刀具路径成形直壁筒，使直壁部分的厚度分布更均匀。文献[8-10]通过优化刀具路径、成形策略、工艺参数等途径均获得了比普通SPIF 更好的厚度分布。

在SPIF 的基础上，一些学者通过在板材下方增加支撑也有效促进了厚度的均匀分布。Li 等[11]采用两点渐进成形改善了圆锥台壁面和转角处的厚度分布。金志浩等[12]在增加凸模支撑的研究中发现，增大原始板材厚度可以提高壁厚均匀临界角。Ben 等[13]使用活性介质作为辅助支撑工具，成形出普通SPIF 难成形的凹凸零件。Kumar 等[14]采用多级液压渐进成形工艺新策略促进了壁厚的均匀分布，解决了薄板过度减薄导致的失效问题。以上研究表明，在渐进成形中增加柔性支撑，有利于控制和促进高成形角和复杂形状零件的厚度分布，提高薄壁板材的成形性能。

本文将静压支撑引入SPIF 中，为悬空板材的下方增加了压力可控的液压油柔性支撑，形成了静压支撑单点渐进成形（Hydraulic support-single point incremental forming，HS-SPIF）工艺。采用Al1060板材单道次成形圆锥台制件，通过有限元仿真和实验验证相结合的方法，定量研究了静压压力对厚向应变分布和材料流动规律的影响，从而获得了厚度分布更均匀的成形制件。

1 HS-SPIF 系统设计

常规的SPIF 是基于“分层制造”的思想，使刀具按照预定义的轨迹对板材进行逐层加工[15]。通过局部变形的累积得到板材制件的最终形状。成形过程中，金属板材边缘需要使用夹具进行夹紧，板材下方的空腔要求能够完全容纳成形制件。当刀具按照预先设计的数控程序逐层挤压板材时，就可以实现钣金零件的数字化制造。在SPIF 的基础上，给板材下方的空腔中增加压力受控的液压油及配套的液压装置，就可以实现HS-SPIF，其原理示意图如图1 所示。液压系统包括油箱、液压泵、溢流阀、压力表、单向阀、密封圈等。通过调节溢流阀和监控压力表，使悬空板材的背部受到压力可控的等静压支撑。HS-SPIF 过程中，在工具头的下压力和液压支撑力的共同作用下，板材沿侧壁方向产生持续的拉伸减薄。板厚由初始的t0逐渐减薄为tp。成形制件侧壁与水平线所夹的角为成形角α。

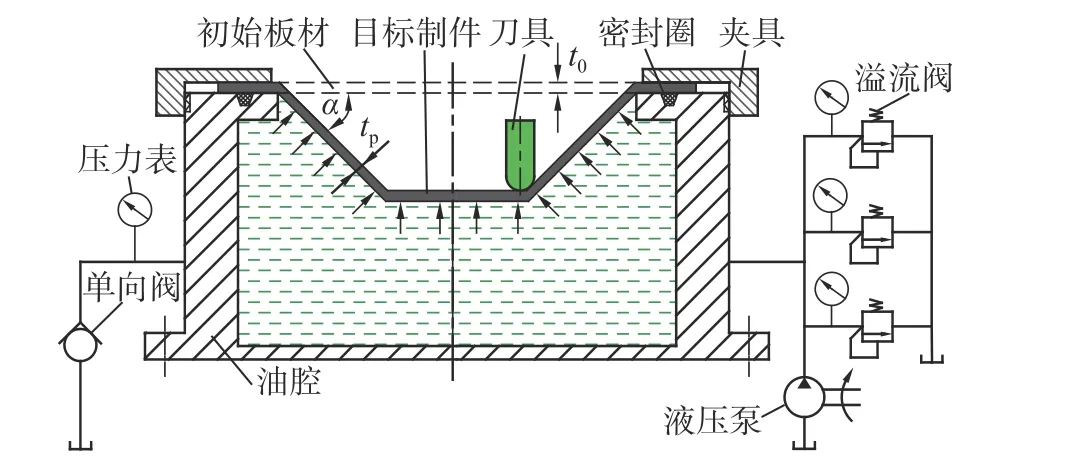
图1 HS-SPIF 原理Fig.1 HS-SPIF principles

2 单道次成形厚向应变理论

在渐进成形中可以假设板材无径向流动，只有剪切变形[12,16]。对于任意的壳体制件，都可以选用三角形单元进行离散化处理[16]，图2 表示三角形单元的剪切模型。

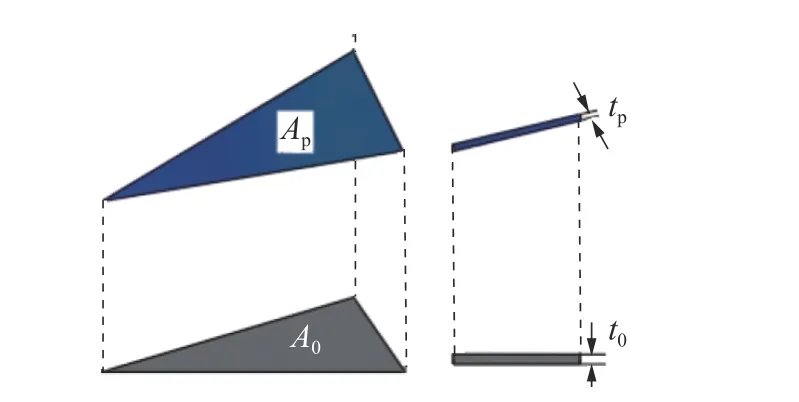
图2 三角单元剪切模型Fig.2 Triangular unit shear model

根据剪切变形机制，三角形单元在垂直于初始单元方向上的投影面积始终等于初始单元的面积。基于体积不变原理有

式中：A0为单元变形前的面积；Ap为单元变形后面积；t0为单元变形前的厚度；tp为单元变形后的厚度。根据式（1）可以得到一个单元最终状态厚度方向的应变εp[16]为

根据式（2）可知，当已知任意三角形单元变形前的厚度t0和变形后的厚度tp时，可以近似估算出HS-SPIF 制件上所有单元和节点的厚向应变。

3 有限元仿真

3.1 有限元模型的建立

利用ABAQUS®/Explicit software 6.14 软件，建立HS-SPIF 简化的有限元模型如图3 所示。初始板材是Al1060 圆形薄板，直径为136 mm，初始厚度为1 mm。成形工具是一个直径为14 mm 的圆柱形棒料球头状刀具，材料是经过淬火处理的高速钢。夹具是一个外圈半径为70 mm，内圈半径为55 mm的刚性圆环。采用S4R 缩减积分的壳体单元进行网格划分。HS-SPIF 有限元模型各参数的定义如表1所示。板材与夹具、板材和工具头之间接触对的摩擦关系采用库仑摩擦模型，板材与夹具之间的摩擦因数设定为0.2，板材与工具头之间的摩擦因数设定为0.1。

表1 HS-SPIF 有限元模型各参数Tab.1 Parameters of HS-SPIF finite element model

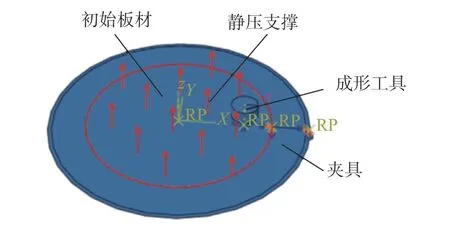
图3 HS-SPIF 的有限元模型Fig.3 Finite element model of HS-SPIF

板材不加压时，模拟成形45°成形角的圆锥台制件的最终形状如图4 所示。从图4 中可以看出，制件侧壁在圆周方向上会逐渐显示出带状的薄壁区域，即“减薄带”。沿制件的Z方向，可以将刀具下压点至结束点之间的加工区域定义为板材的主变形区Ⅲ；将板材上边缘和板材底部不参与变形的区域定义为顶部微变形区Ⅰ和底部微变形区Ⅴ；将微变形区Ⅰ、Ⅴ和主变形区Ⅲ之间的区域定义为顶部过渡变形区Ⅱ和底部过渡变形区Ⅳ。

图4 模拟的最终形状Fig.4 Simulated final shape

将成形圆锥台的CAD 模型导入NX CAM 10.0 中，生成工具头运动轨迹。采用等高线轮廓铣加工，成形过程中的层间距设定为0.5 mm。图5 表示成形圆锥台的等高轮廓铣的刀具运动轨迹。有限元仿真和实验测试中，单道次HS-SPIF 圆锥台的成形角是45°，顶径为70 mm，高度为24 mm。

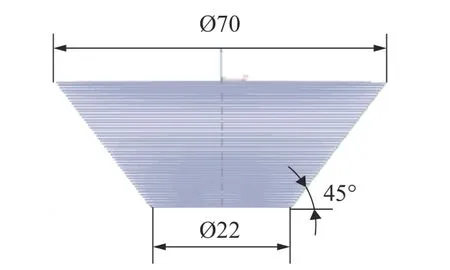
图5 刀具运动轨迹Fig.5 Tool trajectory

3.2 仿真结果及其分析

在0 ～ 0.19 MPa 的静压支撑范围内，每隔0.01 MPa分别成形45°壁角的圆锥台制件。结果发现当静压压力为0.19 MPa 时，主变形区Ⅲ前1/3 左右位置的厚向应变过大而导致成形中断，因此0.19 MPa 的静压支撑成形失败。图6a）表示板材初始状态的厚向应变分布。图6b）～ 图6f）表示静压压力为0 MPa（即无支撑SPIF）、0.06 MPa、0.12 MPa、0.16 MPa和0.18 MPa 时的厚向应变分布云图。从图6b）可以看出，在主变形区Ⅲ的前1/3 区域内，无支撑的SPIF 出现了明显的减薄带，这也是厚向应变绝对值最大、最易出现破裂的区域。当静压压力逐渐增大时，减薄带开始向板材中心扩散；从0 ～ 0.18 MPa，主成形区Ⅲ内发生了“拉料运动”，蓝色区域的面积越来越大，而颜色却越来越浅；到达0.18 MPa 时，减薄带接近消失。这表明0 ～ 0.18 MPa 范围内，压力越大厚向应变值越稳定，板材壁厚分布也就越均匀。随着静压压力的增大，刀具下压点从初始位置A（34，0）移动到A1、A2、A3、A4再到A5（33.47，0.07）；主变形区Ⅲ内的一点从初始位置B（34，0）移动到B1、B2、B3、B4再到B5（29.37，0.37）。通过材料点位置的移动，定量表明了0 ～ 0.18 MPa 的静压压力可以促进材料向不参与成形的板材中心拉入。

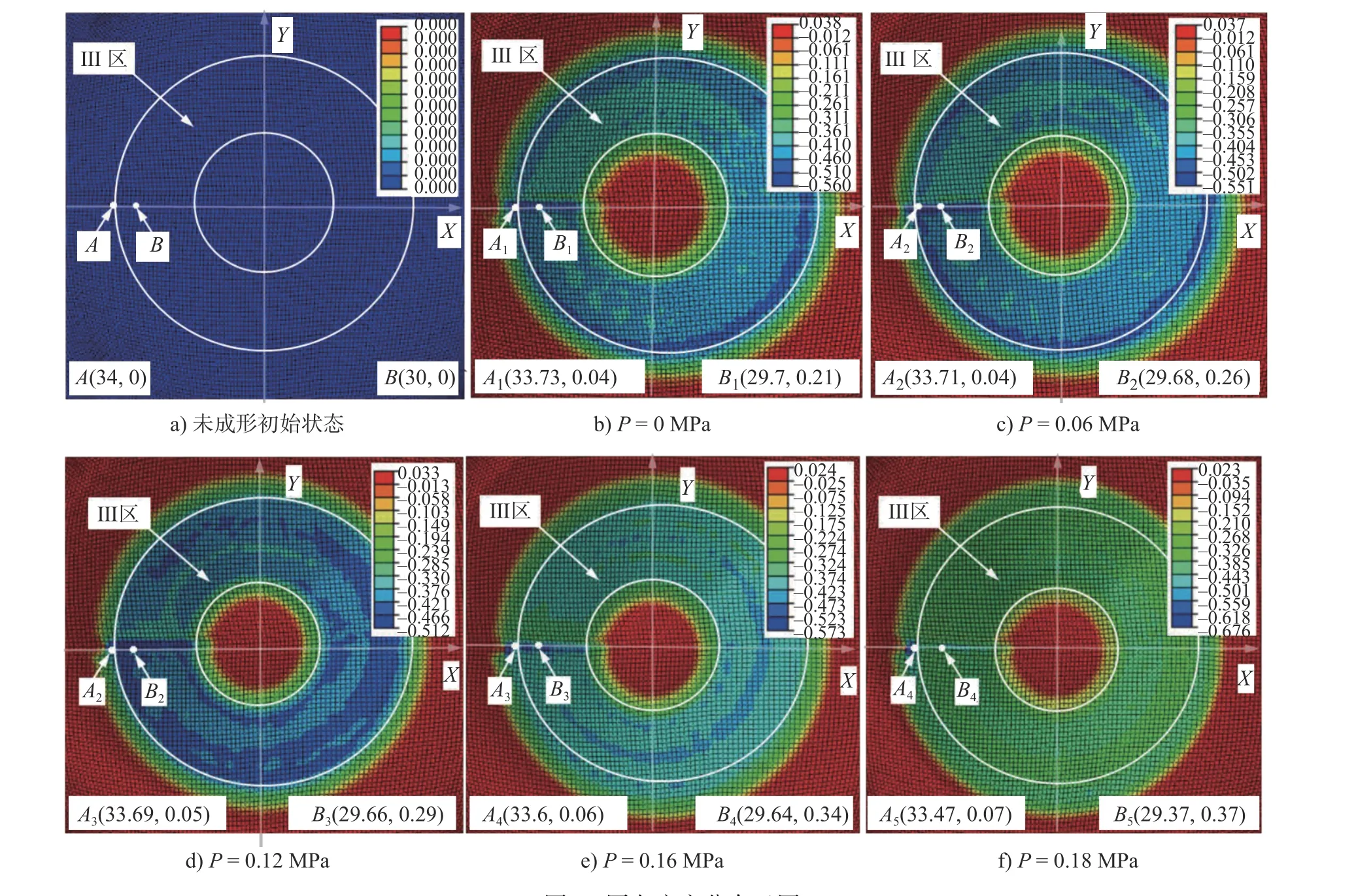
图6 厚向应变分布云图Fig.6 Thickness-strain distribution cloud

从图6b）～ 图6f）可以看出：沿Y轴方向的厚向应变远离刀具下压点，且关于板材中心对称。静压支撑对微变形区Ⅰ和Ⅴ（见红色区域）的厚向应变影响很小，对主变形区Ⅲ的厚向应变影响最大。因此板材厚向应变分布的分析可以简化为前半段Y方向上变形区Ⅱ、Ⅲ、Ⅳ的研究。

各压力下前半段Y方向上变形区Ⅱ、Ⅲ、Ⅳ的厚向应变分布如图7 所示。图中箭头表示材料的运动趋势（标记为①和②）。图7a）中，Ⅱ区在Y方向前2/3 范围内（Y截面约26 ～ 30 mm），厚向应变分布趋势相似且均大于0；随着压力的增大，厚向应变逐渐增大；与无支撑的SPIF 相比，HS-SPIF 的厚向应变增加了0 ～ 0.017。在后1/3 的范围内（Y截面约30 ～ 32 mm），厚向应变急剧减小且均小于0；压力越大，厚向应变下降越快；与无支撑的SPIF 相比，HS-SPIF 的厚向应变减小了0 ～ 0.143。Y截面约30 mm 处的突变，与刀具下压点和大的工具头半径对板材的挤压有关。这表明在顶部过渡变形区Ⅱ内，材料先发生挤压变形再发生拉伸变形。因此随着液压压力的增大，更多的材料可以由过渡变形区Ⅱ流入主变形区Ⅲ。

图7 静压支撑对不同区域厚向应变的影响Fig.7 Effect of hydrostatic support on thickness strain in different regions

图7b）中，Ⅲ区整体厚向应变均小于0，这表明材料发生了向外移动，产生了拉应力状态。各压力下，整体厚向应变最小值集中于主变形区Ⅲ前1/3 左右的位置（Y方向约36 ～ 40 mm），这表明此位置最容易出现过度减薄、塌陷或破裂。在Ⅲ区Y方向约36 ～ 45 mm 处,整体厚向应变的绝对值随着压力的增大而减小，0 MPa 时厚向应变最先到达临界值（-0.461）。这说明，与HP-SPIF 相比，无支撑的SPIF 的裂纹会更早出现在Ⅲ区前1/3 左右的位置；静压支撑有助于促进Ⅲ区的厚向应变分布和材料的均匀流动，而且支撑压力越大材料流动的越均匀。这与图6 的分析结果一致。

图7c）中，各压力下的厚向应变分布趋势相似并接近一致。Y方向约59 mm 之前，整体厚向应变小于0，材料向外流动；约59 mm 之后，整体厚向应变变化很小但都大于0；与SPIF 相比，HS-SPIF 在Ⅳ区厚向应变的变化范围是0.001 ～ 0.003。这说明，静压压力对Ⅳ的材料流动影响不大。

4 实验验证

4.1 实验装置

HS-SPIF 成形设备主要包括MVC510 立式数控机床、成形刀具、板材夹具和液压系统，如图8 所示。实验前将待成形板材放置在油腔的上表面，然后安装夹具夹紧板材。实验过程中，通过调节溢流阀和监控压力表，对静压压力实现定量控制。

图8 HS-SPIF 实验装置Fig.8 HS-SPIF Experimental Device

4.2 实验参数

实验选用的初始板材、成形工具、夹具、层间距及进给速度等参数均与仿真模拟保持一致。通过NX CAM 10.0 生成成形轨迹和相应的加工程序。程序处理后输入到数控立式铣床，通过控制工具头的运动实现45°成形角圆锥台的加工。为了对数值模拟结果进行验证，在0 MPa、0.06 MPa、0.12 MPa、0.16 MPa、0.18 MPa、0.19 MPa 的静压支撑下分别进行实验。

4.3 静压支撑对厚向应变的影响

按照实验方案，采用HS-SPIF 工艺单道次成形45°壁角的圆锥台制件。当静压压力为0.19 MPa时，成形过程出现了异常响声，立即泄压并终止成形后发现板材表面出现了细微的裂纹，如图9 所示。

图9 0.19 MPa 的成形制件Fig.9 Formed parts of 0.19 MPa

0.19 MPa 下的静压支撑成形失败是由于板材受到过大的支撑压力和向下的成形力时，材料流动过快，易于引起局部厚度的过渡减薄。经测量发现，裂纹出现在主变形区前1/3 左右的位置，这与图6 和图7 的分析结果一致。对0 ～ 0.18 MPa 压力下成形成功的制件沿Y向在进行线切割，切割后的半剖试件如图10 所示。将半剖试件沿Y向被进行刻度划分。每隔1 mm 设置1 个测量点。使用螺旋测微器测出各点的厚度后，通过式（2）计算出相应的厚向应变。

图10 切割试件半剖图Fig.10 Cutting specimen half-section diagram

当静压压力为0 MPa 和0.16 MPa 时，沿Y方向前半段路径上的实验和模拟的厚向应变分布曲线如图11 和图12 所示。结果表明：相同支撑压力下，结果的分布趋势接近一致；顶部微变形区Ⅰ和底部微变形区Ⅴ的厚向应变都接近0；0.16 MPa 时，主变形区Ⅲ的实验与模拟结果相差较大。这说明支撑压力对微变形区域Ⅰ和Ⅴ的厚向应变几乎不产生影响，对主变形区Ⅲ的影响最大，与图6 和图7 的模拟结果一致。同时，与模拟结果相比，Y方向约30 ～ 40 mm内的实验结果右移了0 ～ 4.2 mm，约为Y路径总长的0 ～ 3.08%；0 MPa 和0.16 MPa 最小厚向应变出现的位置右移了2.174 mm 和1.1 mm，约为Y路径总长的1.59%和0.808%，有静压支撑的误差小于无支撑的误差。这是由于模拟中所建立的模型比较理想，只有剪切变形；而实验过程中，工具头在每一层加工轨迹上都会发生顺时针运动，使材料在径向也发生了流动，有静压支撑时材料流动的更快。由于右移的位移在允许的误差范围内，因此仿真结果有效。不同静压压力（0 MPa、0.16 MPa、0.17 MPa、0.18 MPa）下，沿Y方向前半段路径上的实验厚向应变分布曲线如图13 所示。从图13 中可以看出，在顶部过渡变形区Ⅱ的①区域（Y路径约26 ～ 30 mm）内，壁向应变随着静压压力的增大而增大。这是由于刀具开始下压时较大的静压支撑使①区域的板材发生了挤压变形。在②区域内（Y路径约31 ～39 mm，位于变形区Ⅱ和Ⅲ内），厚向应变急剧下降，且压力越大，其值下降越快（即斜率越大）。这是由于向上的静压支撑和向下的工具头共同挤压板材时，可以使塑性材料发生更快的流动。这表明，实验中0 ～ 0.18 MPa 的静压支撑有利于Ⅱ区和Ⅲ区的材料的加工成形。在主变形区Ⅲ的③区域（Y路径约40 ～ 48 mm）内，压力越大厚向应变值越大（绝对值越小）。这是由于较大的静压支撑可以使Ⅱ区的更多材料流向Ⅲ区。这表明实验中0 ～ 0.18 MPa 的静压支撑有利于Ⅲ区厚向应变的均匀分布，防止厚度的过度减薄。同时发现，不同静压压力下，实验最小厚向应变出现的位置均在主变形区Ⅲ的前1/3 左右处（Y路径约38 ～ 41 mm），实验结果与模拟结果基本一致。

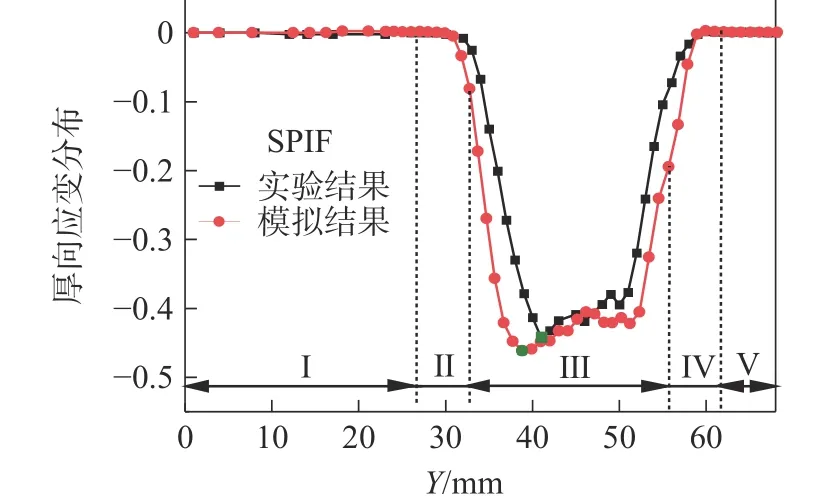
图11 SPIF 厚向应变分布（0 MPa）Fig.11 Thickness-strain distribution of SPIF （0 MPa）

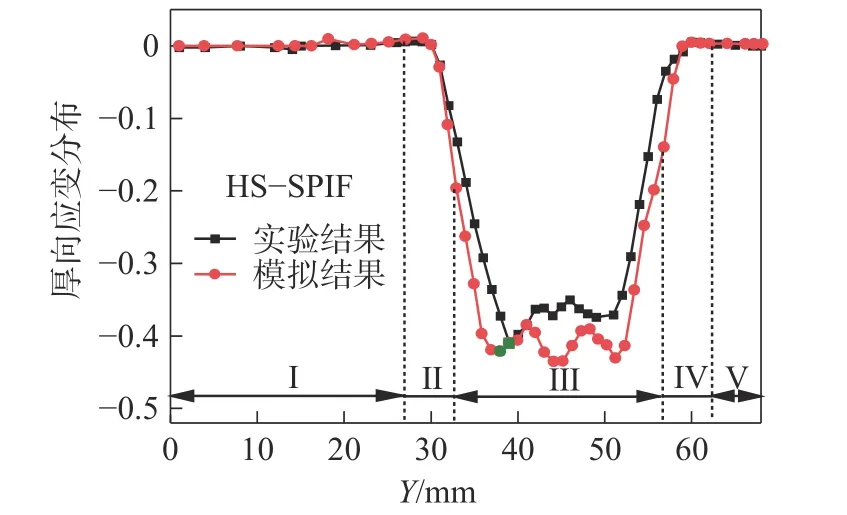
图12 HS-SPIF 厚向应变分布（0.16 MPa）Fig.12 Thickness strain distribution of HS-SPIF （0.16 MPa）

图13 各压力下的实验厚向应变分布Fig.13 Experimental thickness strain distribution of different pressures

5 结论

1）HS-SPIF 过程中，对于厚度为1 mm 的Al1060板材单道次成形45°壁角的圆锥台制件而言，厚向应变分布有利的静压压力范围是0 ～ 0.18 MPa。在此范围内，较大的静压压力会在刀具下压点附近对材料产生更大的挤压变形，有利于过渡变形区Ⅱ的快速成形，有利于主变形区Ⅲ的厚向应变分布。

2）静压支撑对微变形区域Ⅰ和Ⅴ的厚向应变分布基本无影响，对底部过渡变形区Ⅳ的厚向应变分布影响甚微，对顶部过渡变形区Ⅱ的厚向应变分布有一定影响，对主变形区Ⅲ厚向应变的分布影响最大。

3）在顶部过渡变形区Ⅱ区内，材料先发生挤压变形再发生拉伸变形。在有利压力范围内，静压压力越大，由过渡变形区Ⅱ流入主变形区Ⅲ的材料越多，对Ⅲ区材料的均匀流动越有利；静压支撑对底部过渡变形区Ⅳ的材料流动影响不大。在主变形区Ⅲ内，材料主要产生拉应力状态；在主变形区Ⅲ前1/3 左右的位置，板材最容易出现过度减薄、塌陷或破裂。

4）在0 ～ 0.18 MPa 的有利压力范围内，HS-SPIF的厚向应变分布优于无支撑的SPIF。因此采用HS-SPIF 工艺在0 ～ 0.18 MPa 的静压支撑下可以使制件获得更佳的壁厚分布、成形性能和成形质量。后期可对成形参数、变压成形策、多道次成形方法对成形性能的影响做进一步研究。