不同负载下滚动轴承的PSO -SSTCA 算法研究

张泽宇 , ，惠记庄，任余，石泽，段雨

（1.长安大学 道路施工技术与装备教育部重点实验室，西安 710064；2.西藏天路股份有限公司 科研中心，拉萨 850000）

滚动轴承是机械装备的重要组成部分，其运行状况的好坏直接影响机械设备能否正常工作[1]。一旦发生损坏，会造成重大经济损失，甚至会对人身安全产生威胁。目前滚动轴承的诊断难点是工作环境较为恶劣且负载不一，故障特征难以提取与识别。

近年来，学者张习习采用概率神经网络实现了电机轴承的故障分类，且对于平滑因子σ需要不断尝试设定的问题，提出了一种基于正余弦优化算法的自适应概率神经网络[2]。Qin 等提出了基于自适应谐波峰度和改进蝙蝠算法的轴承故障诊断方法，解决了工作噪声影响最优谐振频带定位的问题[3]。Zhao 等利用BiLSTM 网络提取轴承振动信号的深度信息，弥补了传统故障诊断方法需要手工提取特征的缺陷[4]。赵恩庆等将小波包能量与决策树算法相结合，对滚动轴承的混合故障进行有效诊断[5]。王化玲等提出了一种基于故障敏感分量的特征提取与改进K 近邻分类器的故障状态辨识方法，降低了特征提取的复杂度[6]。Che 等提出了一种基于堆叠降噪自动编码器和卷积神经网络的智能故障诊断模型，避免了时间序列和噪声对振动信号的干扰[7]。以上学者对轴承故障进行了诊断研究，但是轴承种类多样且故障复杂，在实践中存在训练数据不足或样本标签缺失等问题，且不同工况下轴承状态数据的分布也不尽相同，难以进行统一分类。

迁移学习可根据不同数据之间的相似关联减少不同数据间的分布差异，进而提高所建模型的鲁棒性。Song 等提出了一种基于改进弹性网络传递学习的故障诊断方法，解决了轴承故障数据获取困难和故障诊断模型训练数据不足等问题[8]。沈飞等提出了一种基于自相关矩阵奇异值分解的特征提取和迁移学习分类器相结合的诊断方法，解决了变负载条件下的电机故障难诊断的问题[9]。Dorri and Ghodsi 在迁移成分分析（Transfer component analysis，TCA）中加入希尔伯特-施密特独立性系数（HSIC），增强特征空间中标签与数据的依赖关系，即半监督迁移学习算法（Semi-supervised domain adaptation via transfer component analysis, SSTCA）[10]。张西宁等提出了一种改进迁移学习方法，解决了训练样本严重不足的问题[11]。以上研究为本文的故障特征迁移学习算法提供了技术支持与理论借鉴。

针对轴承故障诊断样本稀缺和迁移学习准确率不高的问题，本文在TCA 迁移学习理论的基础上，引入HISC 关联和粒子群优化的半监督迁移学习（PSO-SSTCA）算法，对滚动轴承数据进行特征提取，构建不同负载工况下的故障数据集，进行特征迁移变换研究。

1 PSO -SSTCA 算法

迁移学习（TCA）的最终目标是根据已有的数据特征集，搜寻一种映射变换，对原始数据特征进行投影，减小源域与目标域之间的边缘分布的距离[12]。假设DS={(xS1,yS1)，(xS2,yS2)，···，(xSn1,ySn2)}为源域，DT={xT1，xT2，···，xTn1}为目标域，迁移学习的任务如图1 所示。

迁移学习方式与其他算法结合拥有各自的优势方向，选择最优的算法尽可能提高不同特征数据集之间的迁移效率。

1） 引入HSIC 关联原始数据标签信息

工程领域当中，原数据集已有相关标签信息，新数据集缺乏相关标签信息。希尔伯特-施密特独立性系数(Hilbert-schmidt independence criterion, HSIC)可表征两组数据之间的相互独立性。通过引入HSIC 来增强特征空间中的数据与类别标签的依赖关系,即SSTCA。将已有标签信息加以利用，可以提高数据特征的迁移效果。假设源域中的特征数据均含有类别标签，目标域中缺乏相关信息。

原始TCA 算法在最小化边缘分布时，采取的参数化核映射的方式，该方法是先给定核函数，然后根据核函数直接获得核矩阵。不同的核函数对应不同的映射，核函数的选择会直接影响P（XS）和Q（XT）分布的相似性，P（XS）和Q（XT）分别为DS和DT的边缘概率分布。为提高在多种负载环境下的迁移能力，通过一定权重将不同核函数组合起来。通过调整多项式核函数的权重系数，可达到较好的特征迁移效果。

2） 通过粒子群优化算法与伪标签学习优化多核函数权重系数

在数据样本量稀缺时，适当将伪标签数据作为训练数据的一部分，可以在一定程度上提高模型训练的精度。在获取一部分目标域伪标签后，即可计算源域与目标域之间的条件分布概率MMD 距离D为

式中：XS为源域；XT为目标域；n1和n2为源域与目标域集的个数；H用于中心化； ϕ (XS)和ϕ(XT)分别为边缘分布P(ϕ(XS))和Q(ϕ(XT))中任意一点，也是P（XS）和Q（XT）的一个映射ϕ。条件分布概率着重于数据特征的类内相似性，通过最小化源域与目标域的条件概率分布距离，可以更好的利用类内特征，进一步优化滚动轴承不同负载下各个工况特征的迁移效果。

对于多核函数组合方式的选择，往往需要在多次计算对比后取最优解，由于粒子群优化算法（PSO）在处理多种参数取最优值的任务上存在优势，其更新规则为：

式中：i为群中的粒子总数，i=1，2，···，N；Xid、Vid分别为粒子当前的速度与位置； ω为惯性因子；C1、C2为加速常速，前者为每个粒子的个体学习因子，后者为每个粒子的社会学习因子；rand（0,1）表示区间 [0，1]上的随机数；Pid为第i个变量的个体极值的第d维；Pgd为全局最优解的第d维，其通过不同粒子之间的信息共享，不断调整自身的速度与位置，最终使所有粒子趋于同一个最优值。

因此，以每次计算的伪标签目标域数据为基础，计算源域与目标域之间的条件分布概率最大均值差异（MMD）距离，将其作为PSO 适应度函数，以最小化距离为目标实现对多核函数权重系数a的选择，最终通过粒子群之间的协同对比，搜寻出最优系数作为此次迁移任务中多核函数构造方式的最优解。

与TCA 类似，半监督迁移学习算法同样需要对目标核矩阵增加距离限制来保留局部几何结构。在保证映射后，空间内两点之间的距离大小不发生改变，需要定义亲密度矩阵M，对角矩阵D，L′=M-D，L′为图拉普拉斯矩阵。则对原始映射变换需要添加的限制条件为mwintr(WTKL′KW)。

综合以上分析，基于PSO 优化后的TCA 算法筛选出一个合适的矩阵W来求解以下目标函数：

式中：tr（WTW）为正则化项，控制W的复杂度，μ为折中系数；L为样本个数的倒数；I为一个单位矩阵；H为中心矩阵；WTKHK～yyHKW=I避免W的平凡解， γ则调节数据标签与映射数据方差之间的平衡。结合TCA 迁移学习理论，将式（4）转化为

对上式进行特征值分解，依据大小取前m个特征值对应的特征向量组成矩阵W。再经过粒子群算法进一步缩小数据特征类内间距，即可得到迁移变换后的最优映射数据。

3） PSO -SSTCA 算法步骤

（1）输入源域数据及其标签DS={(xS1,yS1)，(xS2,yS2)，···，(xS n1,yS n2)}， 目 标 域 数 据DT={xT1，xT2，···，xTn1}，粒子群算法参数。

（2） 确定初始系数μ，根据源域数据XS与目标域数据XT构建多核函数矩阵K，距离矩阵L以及中心矩阵H。

（3）计算源域与目标域各元素的欧式距离，构造矩阵L'。

（4）求解[K(L+λL′)K+µI]-1(KHK˜yyHK)特征矩阵，并选择前m个特征向量构造迁移变换矩阵W。

（5）得到目标域伪标签，计算两域之间的条件概率分布MMD 距离，以此为适应度值导入PSO，得到最优多核函数构造方式以及最终变换矩阵W。

（6）输出：迁移变换后矩阵W。

2 滚动轴承振动信号的特征提取

引用美国凯斯西储大学电气工程实验室的数据进行研究[13]，驱动端故障轴承数据的基本参数如表1 所示，振动信号数据如图2 所示。

表1 待测故障滚动轴承参数Tab.1 Parameters of faulty rolling bearings to be tested

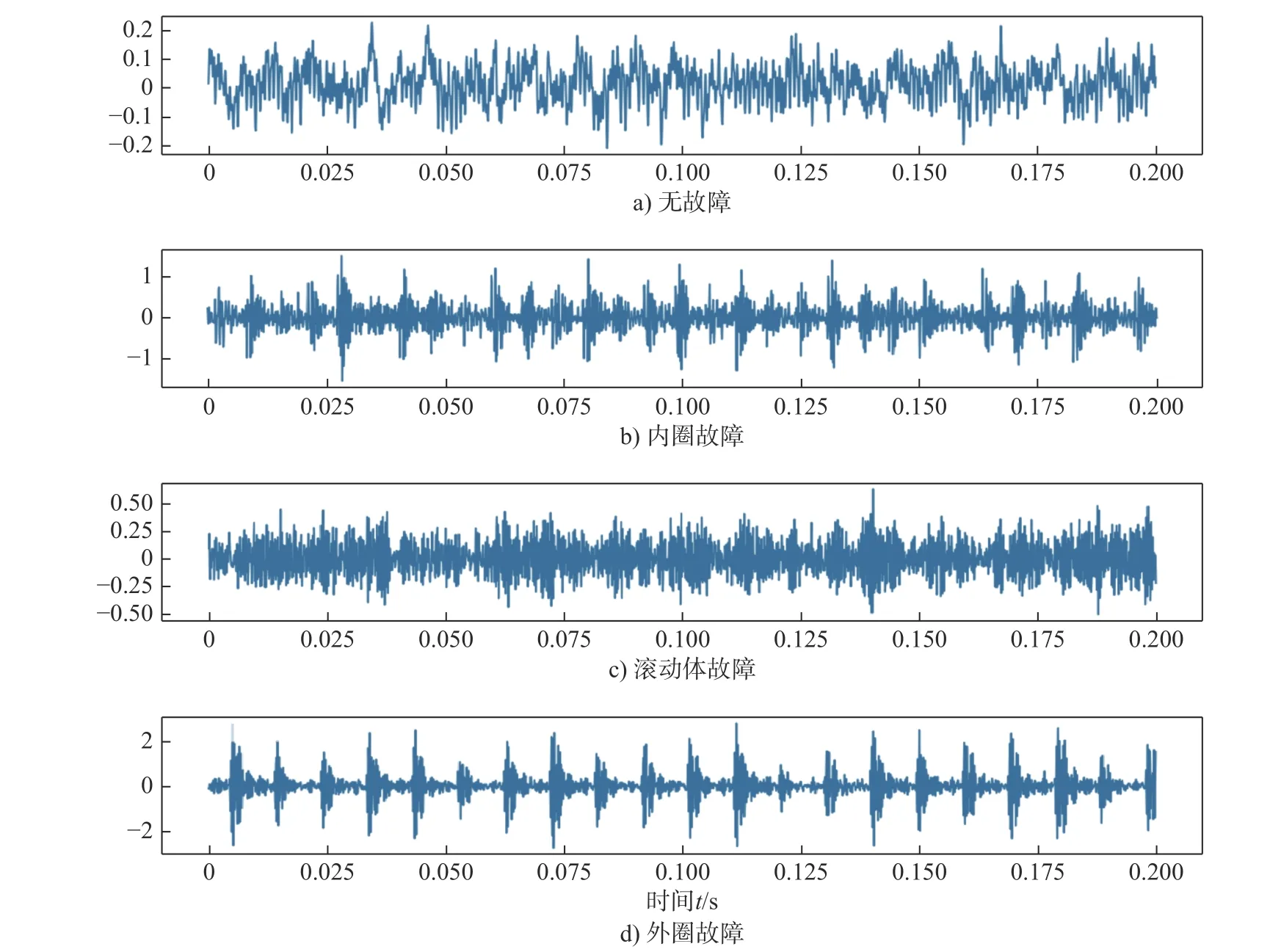
图2 轴承振动信号数据Fig.2 Bearing vibration signal data

对原始振动信号进行小波包最优基分解树的降噪滤波（详见文献[14]）。振动信号的特征通常包含时域、频域以及时频域混合特征，其内部共有18 个特征指标，是能够表征滚动轴承设备运行状态的主要特征指标。对上述实验室内圈、外圈故障以及无故障轴承振动信号进行EMD4 尺度分解，获取时频域中的熵值特征。特征指标计算如表2 ～ 表4所示。

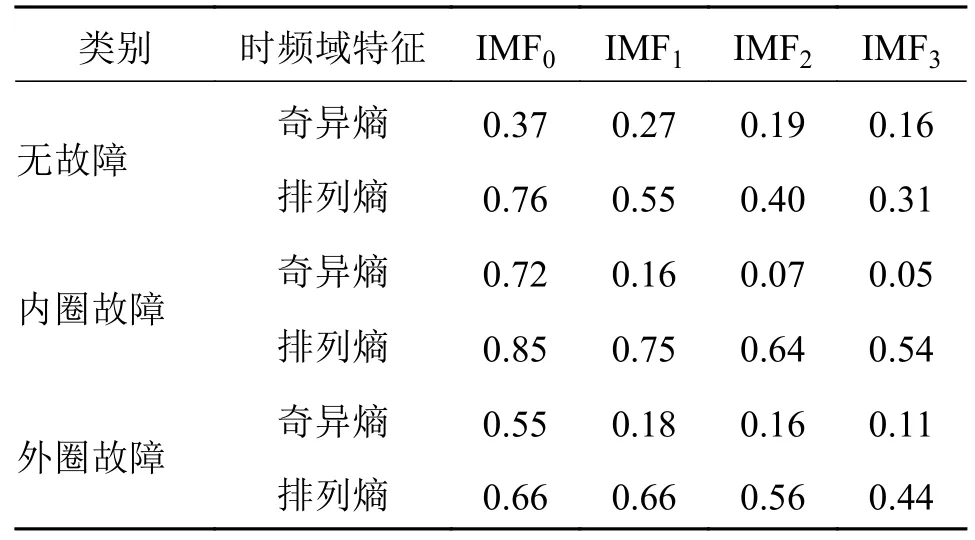
表2 滚动轴承重构信号时域计算结果Tab.2 Rolling bearing reconstruction signals' time domain calculation results

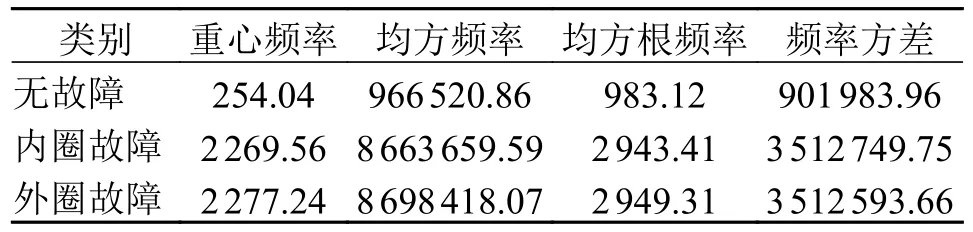
表3 滚动轴承重构信号频域计算结果Tab.3 Rolling bearing reconstruction signal frequency domain calculation results

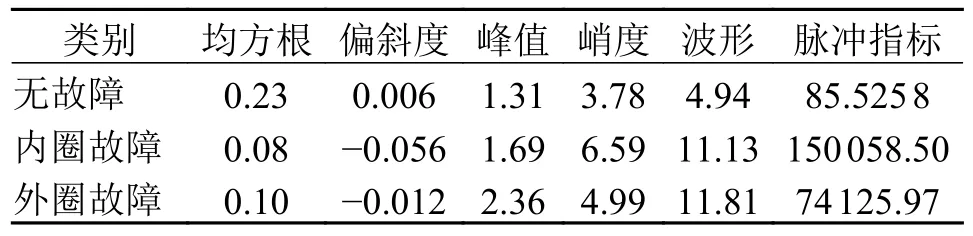
表4 滚动轴承重构信号时频域计算结果Tab.4 Rolling bearing reconstruction signal time-frequency domain calculation results

由表2 ～ 表4 可知：1）峭度、波形指标与脉冲指标能反映信号中的异常冲击成分。因此无故障轴承相较于内外圈故障轴承的计算数据偏低，这些指标可以有效促进判断工程轴承有无故障。而在时频域特征中，根据各IMF 分量计算得到的奇异熵与排列熵值则在一定程度上有助于区分具体故障类别。2）根据表中计算得到的18 个特征，可以形容原始信号所反映出的轴承工作状态。但信号特征的计算具有单一确定性，当负载、环境发生变化时，可能会使原有特征在同一类型状态工作时发生偏移，尤其针对工程装备轴承所处的工作环境。因此，当在不同负载下的数据信号混合应用于状态分析时，需要考虑进行适当的特征变换以减小不同数据分布之间的差异。

3 不同负载下滚动轴承数据特征迁移

对实验数据信号进行模拟混合工程机械的作业，通过特征变换减小不同数据分布之间的差异。

3.1 不同负载下滚动轴承的故障数据集构造

在原有实验室轴承数据的基础上，构造不同负载工况下各个工况的数据组，如表5 所示。

表5 不同负载工况滚动轴承振动信号数据集构造Tab.5 Construction of rolling bearing vibration signal dataset for different loading conditions

表5 中数据组包含A、B、C、D 这4 类，分别对应滚动轴承在0 W、735.49 W、1470.98 W、2 206.47 W功率下的振动信号信息，每组数据包含无故障与不同故障程度下的内圈、滚动体、外圈故障数据。其中样本数量“10”表示从重构信号数据中提取10 组信号片段。每个片段包含2 400 个采样点。

将以上数据信号片段经过小波包降噪滤波及特征[14]提取后，每个数据组最终得到90（或100）*18维的滚动轴承特征数据库，每一个信号片段提取得到的特征形式（如表2～表4 所示）形成各个数据组的特征数据库。由于各个数据组之间存在数据分布差异，通过PSO-SSTCA 的算法来缩短各个特征之间的距离，实现不同负载数据之间的类比分类。

3.2 滚动轴承特征迁移学习结果分析

为体现迁移学习算法对特征的映射能力，本节以线性特征降维方法中常用的主成分分析法（Principle component analysis, PCA）作为对比。以4种不同负载的数据集A、B、C、D 两两进行迁移诊断，共12 种单-单负载判断任务。以特征数据集D 与C 为例，将原始特征数据分别经过主成分分析与迁移学习变换后进行对比。为方便计算特征的可视化，设置映射后的低维空间维度为四维，各个特征表征如图3 和图4 所示。

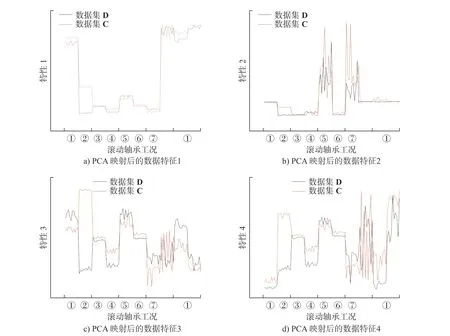
图3 D、C 数据集PCA 映射后的四维特征Fig.3 Four-dimensional features after PCA mapping for D and C datasets

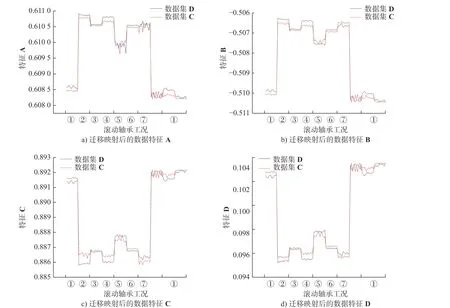
图4 D、C 数据集迁移变换后的四维特征Fig.4 Four-dimensional features of D and C datasets after migration transformation

图3 和图4 中：①～⑦分别为正常工况，0.177 8 mm下的内圈、滚动体、外圈故障，0.533 4 mm 的内圈、滚动体、外圈故障工况。观察以上特征关系图可以发现，高维特征经主成分分析变换后，仅在贡献率最大的特征1 处实现了各个工况的明显区分以及不同数据集D、C（不同负载）的分布对齐。而其余特征则出现明显的特征错位，难以有效区分轴承不同工况。究其原因是不同负载下轴承振动信号的多源数据特征之间往往存在非线性联系，而PCA 属线性降维，因此导致在其他维度呈现出与原始工况不相关的特征映射。而经过迁移映射变换后，两个不同数据集则存在近似相同的特征变化趋势。上述结果表明PSO-SSTCA 方法能够有效降低因负载不同而产生的特征分布差异，提高复杂负载工况下轴承的分类诊断效率。

获取相近的两组数据集后，根据已有数据集及其标签信息对其它数据集使用K-近邻进行分类[15]。通过对比单-单和多-单负载情况下未经处理的原始数据、重构信号、重构后TCA 以及迁移学习算法（PSO-SSTCA）对特征数据的处理能力，并以K-近邻算法（K-Nearest neighbor，KNN）算法对处理数据进行分类，故障准确率如表6 所示。

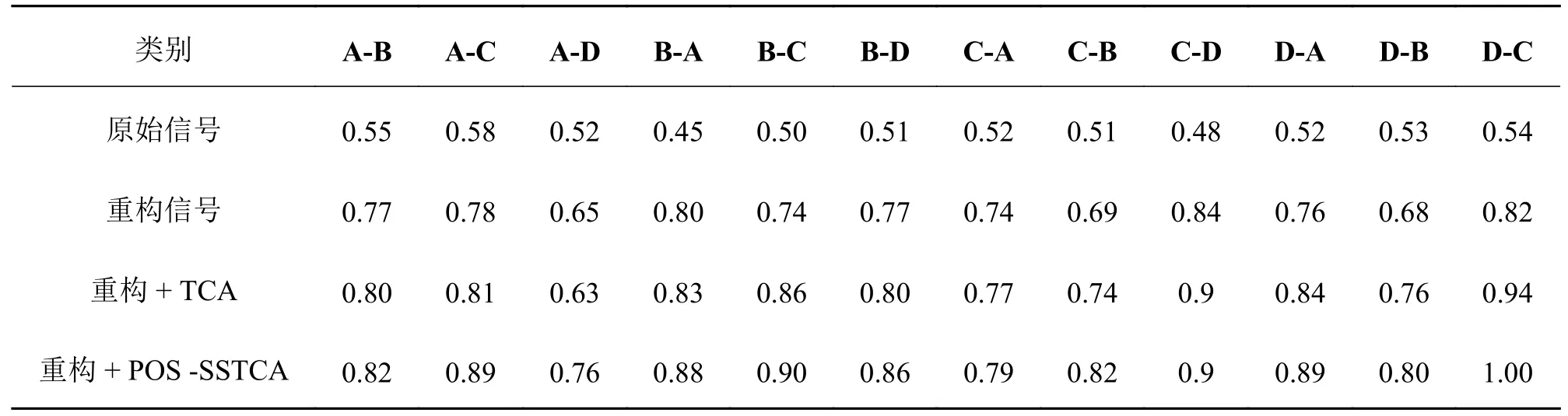
表6 单-单负载情况下各算法诊断准确率Tab.6 Diagnostic accuracy of each algorithm in single - single load case

实际工程中，单-单负载之间的诊断较为理想化，没有考虑不同负载之间的变换趋势，而多数情况下采集得来的数据为包含多种负载工况下的数据集。若将多个数据特征联合起来，可以在一定程度上提高模型迁移适用度。因此添加多-单负载数据集进行对比计算，如表7 所示。

表7 多-单负载情况下各算法诊断准确率Tab.7 Diagnostic accuracy of each algorithm in the case of multiple-single load

由表7 可知：1）未经处理的原始数据在进行变负载故障诊断时，准确率普遍较低，究其原因是背景噪声干扰以及不同负载下的数据存在一定的分布差异；2）在信号经过小波包降噪滤波重构后，传统TCA 方法能在一定程度上解决了数据间因环境因素产生的差距，但由于没有充分利用原始数据故障标签，进行特征映射存在一定的随机性，且最终精度也受初始核函数选择的影响；3）POS-SSTCA 滚动轴承故障诊断算法解决了上述问题。最终通过计算得出各方法的平均准确率：在单-单不同负载环境工况下，原始数据、重构信号、重构后TCA 和PSOSSTCA 的平均准确率分别为51.75%，75.17%，81.25%和85.92%，而多-单负载环境工况下，原始数据、重构信号、重构后TCA 和PSO -SSTCA 的平均准确率分别为61.67%，68.58%，81.25%和88%，准确率相较于前几者均有所提升。

4 结论

1）本文在TCA 迁移学习算法的基础上，引入了HSIC 与多核函数组合的方式，利用原始数据标签信息、多核函数、伪标签学习和粒子群优化算法，进而构造了PSO -SSTCA 迁移算法。

2）通过对滚动轴承的振动信号小波包降噪滤波后，进行故障特征提取，进而对滚动轴承重构信号的时域、频域和时频域进行计算，构造了各个数据组的滚动轴承特征指标数据库。

3）通过PSO -SSTCA 算法实现不同负载数据的特征迁移，构造了单-单和多-单负载情况下滚动轴承的数据集，并使用K-近邻算法对数据集诊断。在两种负载情况下，经PSO -SSTCA 算法的平均准确率相较于原始重构信号分别提升了10.75%和19.42%。

4）本文提出的PSO -SSTCA 算法可以有效地提高滚动轴承在不同负载下的特征迁移准确率及解决样本稀缺问题。