聚焦结构化教学，培养结构化思维

夏建华

（山东省威海市实验小学，山东 威海 264200）

数学是一门抽象的学科，包含的概念、公式繁多。当前在小学数学课堂中，存在知识零散、学习浅层、思维离散，缺乏学科融通等问题。《义务教育数学课程标准（2022 年版）》指出：“在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质，对未来学习有支撑意义的结构化的数学知识体系。”由此看出，新课标强调从整体的视角进行结构化教学，让零散的、孤立的知识通过关联建立起联系，形成有意义的知识结构。单元教学结构化，则是抓住学科特质展开深入研究的好视角，它以教材为基础，用系统的观点对具有内在关联性的教学内容进行分析、整合、重构等，从而优化单元教学结构。因此，教学中教师要以单元整体为视角，聚焦结构化教学，以结构化思想为统领，以结构化任务为驱动，引领学生对学习任务和内容展开结构化理解，培养结构化思维，发展核心素养。

一、单元内迁移，关联思维结构

单元结构化学习，是对单元碎片化知识的系统性建构。基于知识原点的结构化学习，是在知识产生的本源处，从知识和思维两个生长点上下功夫，实现学习的结构化。在单元整体教学中，教师在通读、深研教材的基础上，要精准找到发力点。一是找准知识原生点，知识结构溯本求源；二是抓住知识连接点，知识经验自然迁移；三是把握知识和思维生长点，生长过程浑然天成。

例如，教学青岛版二上《解决问题》这一单元。本单元的重点是理解两步计算问题的数量关系，难点是分步解决两步计算问题的一般思路和解题策略。教学内容包含窗1《乘加乘减问题》和窗2《除加除减问题》，二者内容虽不同，但学习结构相同。其中《乘加乘减问题》既是本单元的起始课，也是本单元的种子课，它的结构化学习将直接迁移到《除加除减问题》的学习中。

课前，通过玩“小猫钓鱼”的游戏，初步感知解决问题的策略，找到两种不同的思考方法：既可以从小猫找到鱼，也可以从鱼找到小猫。

接着，通过设计“到威海华夏城进行解决问题的线上研学”等一系列活动探索解决问题的策略。

活动一：进入海洋馆之前，要买票，一人一张。学生6 人一组，有5 个组，还有老师4 人，一共有多少人？

活动二：“水母表演展厅”里红色的水母和蓝色的水母正在跳舞。

信息1：红色水母有35 只；信息2：红色水母有7 组；信息3：红色水母有7 组，每组5 只；信息4：蓝色水母有4 只；信息5：紫色水母有6 只。

从上述信息中，选择合适的信息，解决红色水母比蓝色水母多多少只？

活动三：回头看，刚才我们解决的这两个问题的思考过程，它们有什么相同点？对比之前学过的解决问题，又有什么不同点？

在活动一中，教师引导学生分别从“问题”和“条件”两个不同的思考角度入手进行梳理，学生逐步清晰地认识到解决问题的关键点有两个：一是可以从条件想起，也可以从问题想起；二是要弄清“先求什么，再求什么”，初步形成解决问题的基本思路。

在活动二中，有了“乘加”的学习基础，教师大胆放手把学习的主动权交给学生，自主解决“乘减”问题。接着，再次引导学生利用结构图这一直观手段，分别从“条件”“问题”两方面入手进行回顾分析，再次梳理了题中的数量关系，从而帮助学生进一步形成解决问题的思路。

在活动三中，通过对比，学生自主发现无论是从条件想起，还是从问题想起，解决此类问题的关键是要确定“先求什么（不知道）”。同时，还会发现今天学习的解决问题其实就是在之前学过的乘法问题的基础上增加了一步。最后回顾本节课的学习历程：首先借助“数学画”来理解题意，接着从条件或问题入手来分析数量关系，最后借助数量关系列式计算成功解决了生活中的问题，这也是解决问题中常用的基本思路。

这种结构化教学中，教师联系学生已有经验，让学习自然发生；关联学生结构经验，让学习深度发生；循环学生再生经验，让学习不断延续。学生在结构化学习的数学体验中，积累数学活动经验，为结构相似的《除加除减问题》做好扎实的铺垫，进一步巩固提升分步解决两步计算问题的一般思路和解题策略。

二、单元内整合，提升思维高度

小学阶段的教材，多以单元的形式，将具有内在联系的知识点编排在一起。在教学前，教师要先读透教材，弄清单元知识的编排逻辑和意图，聚集单元主题及单元教学任务；再基于单元视角确定课时教学任务，并在课时教学中以问题引领学生进行探究，找到与其关联内容、结构相近的“点”，同步进行沟通联系、对比辨析，以获得深度的整体认知，从而实现结构化的建构学习。

例如，教学青岛版五上《方向与位置》这一单元。本单元安排了两个信息窗，窗1《用数对确定位置》和窗2《根据方向和距离确定位置》，教学共同点都是确定物体的位置，发展空间观念。为了让本单元的知识脉络更加清晰，在学生学习了本单元的两个信息窗之后，教师随即设计如下问题串，引领学生深度思考：

问题一：回想一下，这一单元我们都研究过哪些确定位置的方法？

问题二：比较一下，这两种确定位置的方法，你觉得它们有什么不同，又有什么相同的地方？

通过组内交流和研讨，学生很快发现二者的不同点：前者，是用列数和行数来确定位置；后者，却是用方向和距离来确定位置的。而对于二者的共同点，因比较抽象，学生不易发现。为此，搭建问题脚手架。

辅助问题1：数对，如果只给你一个列数或行数，能确定位置吗？为什么？如果同时都给呢？

辅助问题2：方向和距离，如果只给方向和角度，能确定位置吗？如果只给距离，能确定位置吗？为什么？如果同时都给呢？

学生自主勾画、假设、讨论后发现：用数对确定位置时，如果只给列数，只能说明它在一条竖线上；如果只给行数，只能说明它在一条横线上。如果同时都给，则两条线相交在一个点上，就是我们要确定的位置；而用方向和距离确定位置时，如果只给方向和角度，只能确定它在一条线上；如果只给距离，只能确定它在一个圆上。如果同时都给，则线与圆相交在一个点上，就是我们要确定的位置。

通过对比，学生顿悟：这两种方法，看似不同，但回到根本上，其实都是在用两个量确定平面上某个点的位置。（图示1）

问题三：以前我们学过在一条线上用一个量来确定位置；现在我们学习，在一个平面内用两个量来确定位置；以后我们还可能遇到什么情况？可能会怎么解决？

瞬间，学生的思维被点燃，展开想象：在立体空间中，可能要用到三个量来确定位置。

这种单元内基于核心问题的整合教学，打破了原来的散点教学，更加注重知识的生长点和延伸点，把每节课知识置于整体知识的体系中，对单元内的知识结构组成进行分析，寻找单元整体与部分之间的内在联系。通过单元整合、前后勾连，疏通脉络，感受数学知识的整体性、逻辑性、迁移性、关联性，直击核心，有效提高了学生的思维高度，最终实现1+1>2。

三、单元内重组，拓展思维深度

有学者认为，数学基础知识的教学，不应求全，而应求联。在单元整体教学中，教师有时需要基于某一改革理念或学生立场去审视教材原来的编排，在吃透教材原来编写意图的基础上发现它的局限性，根据学生的认知经验及学情分析提出新的设想，对单元教材内容进行整合重组，按照新的结构体系开展教学实践。

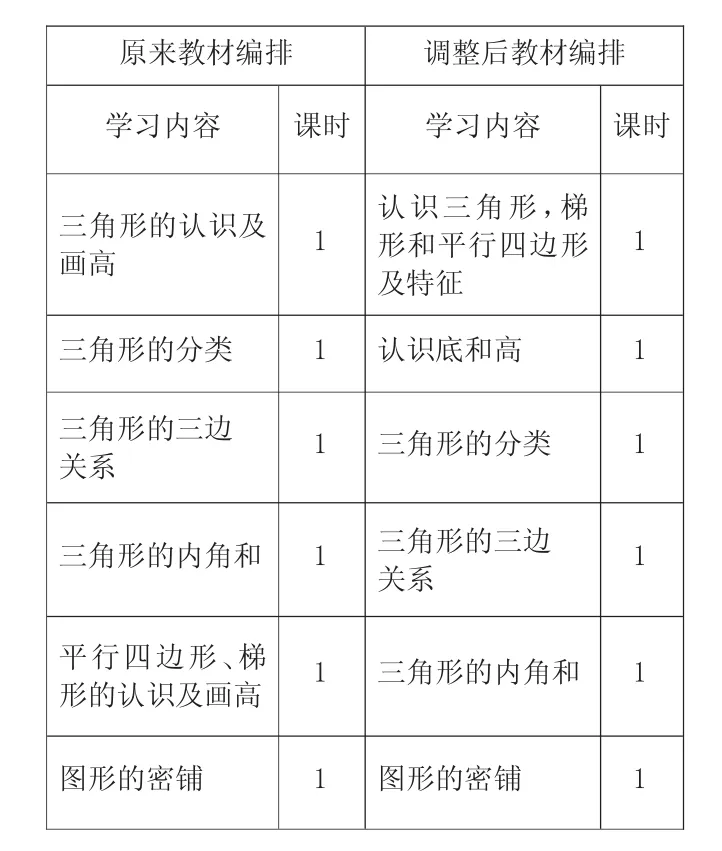
例如，青岛版四上《认识多边形》这一单元。这一单元安排了三个信息窗，分别是窗1《认识三角形》，窗2《三角形三边关系与内角和》，窗3《认识平行四边形和梯形》。其中，关于“高”的教学，一直都是这一单元的难点。教材原来的编排是分散在不同课时进行学习：窗1 中先认识三角形的底和高；窗3 中再认识平行四边形和梯形的底和高。这三种平面图形的高，彼此之间过于零散，缺乏沟通，很明显这样的结构编排不利于学生对高的本质把握。依据单元整体教学理念，可以创造性地将这三种平面图形的高融合在一课时进行探究，并设计如下递进性问题学习任务链，让探究逐渐走向深入，接近核心概念的本质。

教材原来编排及调整后的编排：

原来教材编排调整后教材编排学习内容课时学习内容课时三角形的认识及画高1认识三角形，梯形和平行四边形及特征1三角形的分类1认识底和高1三角形的三边关系1三角形的分类1三角形的内角和1三角形的三边关系1平行四边形、梯形的认识及画高1三角形的内角和1图形的密铺1图形的密铺1

《认识底和高》课时教学任务链：

第一链，由“树高”引入到“三角形的高”

①这里有一棵小树，你认为从哪里到哪里才算是树的高？

②现在刮台风，小树歪了，小树的高在哪里呢？

③小树有高度，那三角形有高吗？请你在图中画出来。

④你觉得给三角形画高，让你联想到以前学过的什么类似的知识？

第二链，由“桥高”引入到“梯形、平行四边形的高”

①一座桥，限高4.5 米。这里的高4.5米指的是从哪里到哪里？

②桥有高度，那梯形有高吗？请你在图中画出来。会有多少条这样的高？

③平行四边形有高吗？尝试在图中画出来。你能画出不同的高吗？

④你觉得给梯形和平行四边形画高，让你联想到以前学过的什么类似知识？

第三链，整合关联，凸显异同——寻找高的本质

①对比这3 种平面图形的高，你有什么发现？它们的相同点是什么？不同点是什么？

②我们今天学习的底和高，对今后的学习有什么用呢？

在上述探究活动中，教师首先利用学生已有的生活经验和知识基础建立起三角形、平行四边形、梯形的高的具象；接着，通过对比学生发现“高”的本质就是“点到直线之间的垂直线段”，这是这三种高的相同点。不同点是三角形的高是指点到直线的垂直线段，而梯形和平行四边形的高则是指平行线之间的垂直线段。这样一节课中同时呈现三种平面图形的高，有利于学生经历完整的问题探究过程，凸显异同，归纳本质。

这种基于单元整体调序后的结构化学习，巧妙地将学生的认知发展规律与知识发生规律相结合，以现有教材为依据，又超越现有的教材。在对“单元目标、教材价值、学生实际”的研究与把握的基础上，对知识进行重构编排，注重加强知识点之间的关联性，建构科学的知识体系，拓展思维深度。

四、打破单元界限，凸现思维本质

为符合学生的数学认知规律，数学教材通常将一些整体性、系统性的知识拆散，安排、穿插在不同年级教材中。同一个知识体系，可能会编排在不同的年级，也可能编排在同一年级的不同单元。教学时，我们可以将教材对课时教学内容相关知识体系的编排看作一个整体，借助这个整体审视课时教学内容的地位和作用以及与前后知识的联系，以它们的共同本质为纽带进行沟通，在共同本质的统摄下规划每个课时的结构化任务，引领学生展开基于结构化理解的迁移性学习，从而更好地将知识融会贯通，促进思维可持续发展。

例如，青岛版五上《分数除法》这一单元。这一单元安排了四个信息窗，其中前2 个窗是关于分数除法的计算，即《分数除以整数》和《一个数除以分数》，是在学生掌握了整数、小数除法计算和分数加、减、乘法计算的基础上进行学习的。《义务教育数学课程标准（2022 年版）》指出：数的运算教学，应注重对整数、小数和分数四则运算的统筹，进一步感悟运算的一致性，从整体上理解和掌握运算的算理和算法，认识计算方法的共性和差异。因此，教学中教师要深入理解数的运算本质，打破零散的、点状的知识碎片，帮助学生建立数的运算知识体系，沟通整数、小数、分数在加、减、乘、除运算中的内部联系，构建系统的认知结构，感悟运算一致性。

在学习《一个数除以分数》这节课中，可以将其置于“运算一致性”这个结构模块中去审视，就会发现该结构系统的共同本质是：先统一计数单位，再用计数单位的个数相除。因此，本节课的教学以“本质沟通”为纽带展开，给学生提供结构化的学习材料。

第一次沟通：将分数除法与分数加减法进行勾连。

第二次沟通：将分数除法与整数除法和小数除法进行勾连。

先复习整数除法，如80÷20 可以看作80 个1 除以20 个1；再复习小数除法，如1.4÷0.2 可以看作14 个0.1 除以2 个0.1；再出示分数除法，如可以看作10 个除以1 个。最后，对比发现分数除法与整数除法和小数除法的运算是一脉相承的，都可以先统一计数单位，再将计数单位个数相除，可以用等分计数单位，也可以用几个计数单位包含几个计数单位。它们的不同是有的是整数，有的是小数，有的是分数。

在上述教学中，教师紧紧抓住“计数单位”这个核心概念，构建以计数单位为抓手的加、减、乘、除运算的整体结构，引导学生在学习活动中不断感悟数的运算的一致性，打通分数除法与整数、小数除法的隔断，加深对数的运算本质的理解。这种共同本质统摄下的迁移性学习，立足“大概念”，能有效地促进学生的结构化学习，凸显思维本质，进而达到“学一点通一类，通一类会一片”的学习效果。

五、结语

总之，数学是一门有结构的学科。结构化的数学学习是一种“大数学”的学习，能有效地培养学生的结构化数学素养。教师在教学中要以整体的视角聚焦结构化教学，把握教学核心，理清知识结构，运用结构化思想展开创造性的研究，引领学生经历结构化的数学学习活动，进而通过教师结构化的教让学生实现结构化的学。学生在合理建构知识的基础上，逐渐形成完整的认知结构、能力结构和思维结构。驻足现在，放眼未来，基于单元整体的小学数学结构化教学，仍需要我们共同努力探索、研究。