考虑频率稳定约束的电网新能源承载能力评估方法及其应用

罗澍忻，朱廷猛，余浩，陈鸿琳，孙海顺，刘瑞宽，彭虹桥，左郑敏，李秋彤

（1.广东电网有限责任公司电网规划研究中心，广州 510080；2.华中科技大学电气与电子工程学院，武汉 430074）

0 引言

由于目前新能源机组无法提供有效转动惯量与调频能力，以新能源为主体的新型电力系统的频率稳定问题开始备受关注。频率作为电力系统安全稳定运行的重要因素，反映了电源侧与负荷侧之间的有功功率平衡情况。相较于常规同步电源，新能源机组对于频率的较弱适应性致使其在极端情况极易脱网，引发功率缺额。同时，非同步电源发电的增加挤占了常规电源的发电空间，电力系统的等效惯量以及一次调频能力遭到弱化，频率稳定问题凸显［1-3］。在英国“8·9”大停电事故中，雷击引起的单相短路接地故障导致电网出现由于机组跳闸，风电振荡降出力等引起的大功率缺额，又因频率变化率（rate of change of frequency，RoCoF）过大而使英国电网分布式电源脱网，进一步引起火电机组跳闸，最终导致系统频率大幅跌落，低频减载动作［4-5］。在澳大利亚南部电网“9·28”大停电事故中，新能源在台风极端天气下大规模脱网后由于低惯量导致频率跌落过快，火电缺乏足够时间响应频率变化，进而引起联络线过载切除，导致电网变为孤岛状态，进一步加大有功缺额，诱发大面积停电［6-7］。2015年9月19日，华东电网在锦苏特高压直流闭锁故障下发生频率跌落事件［8］。经事后分析，系统的低惯量水平与弱调频能力是三起事故的重要诱因。

对于受到功率缺额扰动后的电力系统，RoCoF和频率跌落最低值作为重要的频率稳定指标，电网新能源承载能力可通过考虑功率不平衡扰动下RoCoF 及频率跌落最低值两个方面约束进行评估［9］。其中，频率最低点的主要影响因素是系统等效惯量、电源的一次调频以及负荷的频率调节效应，频率变化率的主要影响因素是系统等效惯量以及不平衡扰动功率大小。大量新能源发电接入后系统的低惯量水平以及弱调频能力的问题将导致指标的恶化。因此，考虑频率稳定约束的电网新能源承载能力的研究应该对系统惯量、不同特性的调频电源以及负荷的功率频率调节效给予重点考虑与关注。

构建考虑不同类型频率调节电源的频率响应模型可以用于对电网新能源承载能力进行有效评估。传统频率稳定分析方法包括基于详细模型的时域仿真法以及对电网采取简化处理的数学解析法［10］。为了对扰动下电力系统的频率响应特性进行准确分析，常采用时域仿真法，但该方法存在模型复杂且对复杂系统的计算量大、运算耗时长的问题。数学解析法主要包括基于平均系统频率（average system frequency，ASF）模型和系统频率响应（system frequency response，SFR）模型的两种频率特性分析方法，其有效提升了频率响应分析的效率。其中，文献［11］提出的SFR 模型将系统等值为单机带负荷的低阶频率响应模型，只是考虑了火电机组原动机与调速器的频率特性，需要结合多种不同特性的频率调节电源的应用，以满足新型电力系统的频率特性分析需求。文献［12］提出的ASF模型保留了对所有参与调频机组的频率响应特性，为涵盖不同特性的频率调节电源提供了模型基础。在其基础上进行拓展，能够建立含多类型调频资源的以新能源为主体的新型电力系统的频率响应模型。

随着新能源发电不断增加以及火力发电阶段性退网，电源侧不确定性增加，高比例新能源并网的电力系统需要适应更大的有功功率缺额事件，仅靠常规电源的传统调频策略已经难以满足频率稳定的需求。因此，需要对“源、网、荷、储”多环节中潜在的快速频率响应资源进行充分挖掘。对于电源侧调频能力的挖掘，提出对传统同步机组调频能力的优化改造，使其在高新能源渗透率电力系统下达到最佳的调频效果［13］。利用直流输电的快速控制特性与过载能力响应大扰动下系统的频率变化也是一种技术途径，文献［14］提出了对直流FLC 参数的优化策略。对于负荷侧的调频能力，不少学者提出通过可中断负荷的主动退出或者柔性负荷的主动调节来快速响应扰动初期的频率变化［15］。对于储能技术的调频能力，储能装置的快速调节能力可在几秒内响应目标出力，可作为应对系统惯量支撑与调频不足问题的有效手段［16］。

目前，新能源具备一次调频能力已经成为欧美国家的普遍要求。为了满足我国以新能源为主体的新型电力系统安全稳定运行需要，许多技术标准均已提出。GB 38755—2019《电力系统安全稳定导则》［17］已经对新能源场站的惯量响应和一次调频能力提出了明确要求，NB/T 10315—2019《风电机组一次调频技术要求与测试规程》［18］与GB/T 40595—2021《并网电源一次调频技术规定及试验导则》［19］则是对各类调频电源尤其是新能源场站的一次调频技术设定了具体的技术规范。关于新能源的调频控制技术的研究，已经取得了一定的研究成果。文献［20］通过降功率运行方式为风电场预留调频备用功率，使其在电网出现功率缺额时参与系统频率调节。文献［21］介绍了西北电网风电场参与电网快速频率响应典型方案，完成了国内首次风电场快速频率响应能力的实测分析，指出风电场的调频特性与常规电源相当。文献［22］对东北电网风电惯量与一次调频进行了现场实测与分析，突破了理论与样机层面的研究，完成了实际风电场试验与应用，对大规模风电参与系统频率支撑的工程应用具备指导价值。综上所述，虽然新能源参与系统调频的研究已较多，但仍主要集中于对传统跟网型新能源发电调频技术的研究。

综上所述，针对高比例新能源导致的低惯量电力系统频率稳定问题，国内外已开展许多相关研究。但是大量工作集中在针对新能源等调频能力的研究，在系统层面如何评估考虑频率稳定约束的电网新能源承载能力以及新型频率控制技术对于电力系统频率稳定性的提升作用等方面则是电网规划与运行控制关注的重要问题，有待进行深入的研究。

本文针对考虑频率稳定约束的电网新能源承载能力及其应用开展研究。首先，建立了考虑不同特性的频率调节电源的系统频率响应模型，并通过时域仿真对模型的有效性进行验证；然后，基于频率响应模型研究了以频率最低值和频率变化率为频率稳定约束的电网新能源承载能力评估方法；最后，对电网新能源承载能力评估以及新能源发电技术对系统频率稳定性的提升作用的研究验证了方法的有效性。

1 系统频率响应模型

1.1 频率响应模型

基于平均系统频率ASF建模方法，可以考虑不同特性的频率调节电源，构建针对高比例新能源接入电网的系统频率响应模型。忽略系统电压动态变化、网架拓扑、同步机功角稳定性以及频率的空间分布性，将所有同步机组的转子运动方程等值聚合，整个系统等值得到频率响应模型，如图1所示。

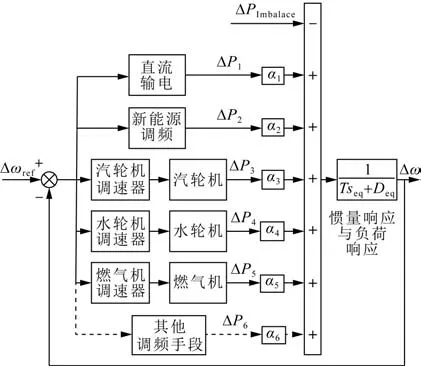
图1 电力系统的频率响应模型Fig.1 Frequency response model of power system

其中，Δω与Δωref分别为系统频率及其参考值；ΔPImbalance为不平衡功率；ΔPi为各类调频资源的输出调频功率。

该模型以ASF模型为基础，建模过程中根据系统调频资源按常规同步电源和参与频率控制的非同步电源两大类考虑，分别建立各类调频资源的频率响应模型。同步电源包括系统内常规火电机组、水电机组、燃气发电等，这类电源的频率响应模型按照原动机分类分别对调速控制及原动机动态建立。非同步电源包括直流输电、新能源发电甚至灵活调控负荷等多种具备不同频率响应特性的调频资源，其频率响应模型与控制有关。

系统的频率响应模型通过对调频资源参与容量比例、负荷频率特性以及等效惯量3 种特征参数的模拟，可以根据待评估系统的不同运行场景，设置对应的特征参数，可以适应含多种调频资源的新型电力系统的频率特性分析，主要包括以下三点。

1）系数αi为各类调频资源参与容量比例，即各类调频资源的可调频容量与容量基值的比值；

2）系数Deq为负荷频率调节效应系数，即系统频率下降（上升）1%，系统有功负荷减少（上升）的百分数，典型值在1～2之间取值；

3）系数Teq为系统的等效惯性时间常数，代表系统所有运行同步机组的等效惯量的聚合，其表达式如式（1）所示。

式中：Tji、STin分别为系统内第i台传统同步发电机的等效惯性时间常数以及额定容量；Sb为系统容量基值；G为同步发电机的集合。

1.2 模型有效性验证

为了验证所建立的频率响应模型的有效性，以PSCAD/EMTDC 仿真软件上搭建的含新能源机组的3机9节点系统作为时域仿真对象，如图2所示。

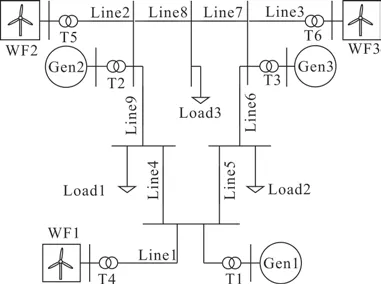
图2 含新能源机组的3机9节点系统Fig.2 Nine-bus system with three machines and renewable energy generation

通过新能源风电机组替代同步机组部分容量，模拟电力系统内新能源渗透率不断提高的过程。系统额定频率为50 Hz，Gen1为水电同步机组，Gen2与Gen3 为火电同步机组，WF1、WF2、WF3 分别为3 个新能源风电场，Load1、Load2、Load3 分别为3个负荷。

算例系统总有功负荷为900 MW，当新能源发电功率占负荷的30%时，剩余的负荷由同步电源出力承担。其中，风电机组运行在最大风功率跟踪模式下，不提供频率支撑，同步机组出力为额定有功功率的90%，预留10% 调频备用容量。Gen1、Gen2 与Gen3 的额定容量分别为305 MW、237 MW与158 MW，额定惯性时间常数TjGeni为16 s、12 s与8.1 s，此时，系统的等效惯性时间常数Teq（2Heq）为10 s。当系统稳定运行时，在t=20 s 时刻系统突增7%的负荷，观察系统频率动态响应的过程。

图3 给出了基于频率响应模型和电磁暂态仿真的算例系统的暂态频率响应曲线。结果显示，电磁暂态仿真与频率响应模型的频率响应波形相近，频率变化率（RoCoF）和频率跌落最低值（fNadir）一致，说明频率响应模型能较好反映系统的频率响应特性，采用频率响应模型能够对电网新能源承载能力进行有效评估。

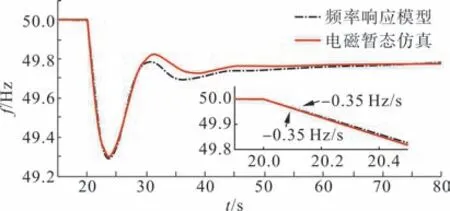
图3 电磁暂态仿真与频率响应模型的系统频率波形对比Fig.3 Comparison of system frequency waveforms of electromagnetic transient simulation and frequency response model

2 电网新能源承载能力评估方法

2.1 频率稳定指标约束

衡量扰动下电力系统频率稳定的关键指标包括最大频率变化率Rmax与频率跌落最低值fNadir。为了评估电网的新能源承载能力，对频率稳定指标考虑如下约束。

1）频率跌落最低值fNadir，是指发生有功功率缺额后频率跌落过程中系统频率所达到的最小值。高比例新能源电力系统的低惯量特性将导致较大的频率跌落幅度，一旦频率触及低频减载保护动作整定值，将引发系统大面积停电。因此，考虑将频率跌落最低值fNadir的约束定义为：

式中按照避免触发低频减载保护动作来考虑，取低频减载动作起动值fUFLS作为fNadir的约束值。

2）频率变化率ΔfRoCoF，是指系统频率变化的速率，决定于不平衡功率和系统惯量大小，其值通常在扰动开始时刻最大。目前电网运行对频率变化率没有统一的约束标准。扰动引发较大的ΔfRoCoF可能引发同步机组的滑极现象，造成结构损坏，燃气机组的运行受频率变化率影响较大，分布式发电以频率变化率为孤岛检测依据，现有风电光伏变流器控制对频率变化率也有相应的约束设置。从电网运行角度，高比例新能源接入系统势必引起电网运行出现较大的频率变化率的场景，如欧洲电网要求在大扰动下系统能够承受1 Hz/s 的频率变化率，而随着新能源渗透率提高，该耐受值未来甚至要提高到2 Hz/s［23］。因此，频率变化率ΔfRoCoF将成为高比例新能源电力系统的重要约束指标，其约束可表示为：

式中：Rmax为扰动瞬间最大频率变化率；Rlimit为频率变化率限制值。

2.2 基于频率约束的电网新能源承载能力评估方法

在给定电网新能源占比和扰动不平衡功率的条件下，可以采用系统频率响应模型计算频率跌落最低值和频率变化率，因此本文提出基于系统频率响应模型的电网新能源承载能力评估方法，其思路是：基于待评估系统的频率响应模型，考虑频率稳定指标fNadir与Rmax的约束，根据新能源占比构建系统的频率稳定域对系统的新能源承载能力进行评估，步骤如下。步骤1：构建频率响应模型。针对待评估电网确定其发电资源与用电负荷的关键参数，其中包括各类调频电源以及负荷的容量、负荷频率调节效应系数以及各同步机组的惯性时间常数与额定容量，计算αi、Deq、Teq三个特征参数，构建反映系统频率特性的频率响应模型。步骤2：明确频率稳定约束。基于待评估电网确定低频减载起动值fUFLS以及频率变化率限制值Rlimit，以fNadir＞fUFLS与Rmax＜Rlimit作为电网新能源承载能力评估的频率约束条件。步骤3：估算频率稳定指标。在不同扰动不平衡功率和新能源占比的场景下，通过频率响应模型对待评估系统的频率跌落最低值fNadir与最大频率变化率Rmax进行估算，得到如图4 所示频率跌落最低值以及频率变化率与新能源占比以及不平衡功率扰动之间的关系。步骤4：构建系统频率稳定域。根据图4 所示fNadir与Rmax的计算结果，在给定fNadir与Rmax两个指标约束条件下，分别确定以新能源占比和不平衡功率扰动为参数的频率稳定约束域，如图5 所示。进一步取两个指标约束域的交集作为待评估系统的频率稳定区域，即该区域内同时满足频率约束（fNadir＞fUFLS与Rmax＜Rlimit），如图6所示。这里频率稳定域的边界代表在给定不平衡功率扰动条件下系统满足频率约束时所能承载的最大新能源占比。图6 中，假定以电网遭受10%不平衡功率扰动为频率稳定考核条件，频率稳定约束值fUFLS与Rlimit分别取值为49 Hz 和-1 Hz/s。指标fNadir与Rmax的约束域显示，系统在32%新能源占比下遭受10%功率缺额后频率将跌落至49 Hz，系统在63%新能源占比下遭受10%功率缺额扰动的初始时刻最大频率变化率将达-1 Hz/s，说明此时电网新能源承载能力受频率跌落最低值约束，不能超过32%。

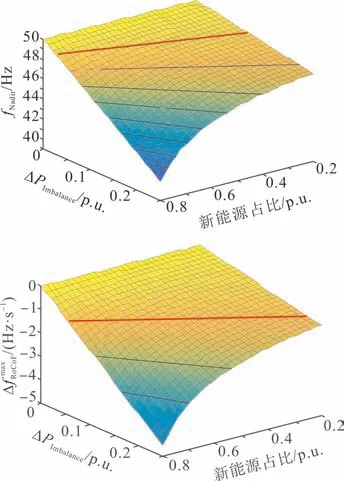
图4 fNadir、Rmax与新能源占比关系Fig.4 The relationship among fNadir,Rmax and the proportion of renewable energy power generation

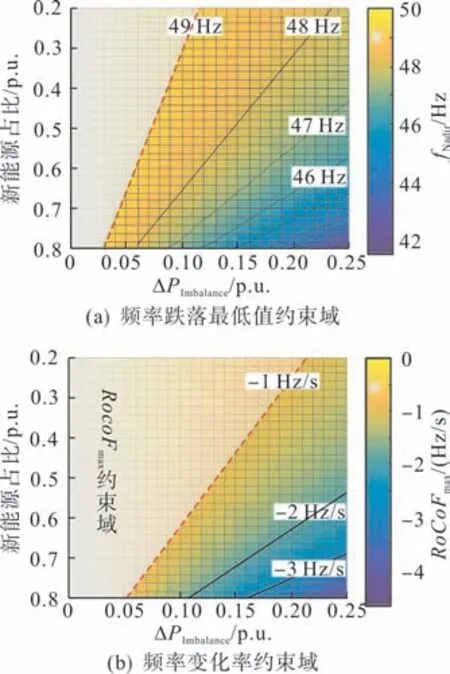
图5 fNadir与Rmax约束域Fig.5 Constraint domain of fNadir and Rmax

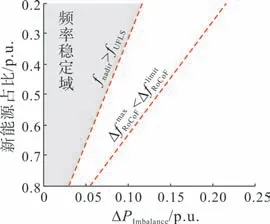
图6 系统的频率稳定域Fig.6 Stability domain of the frequency of the power system

3 评估方法的应用

3.1 基于频率响应模型的电网新能源承载能力评估

3.1.1 算例介绍目前，在国内实际工程应用中投入运行的新能源机组普遍不具备辅助调频的能力，电力系统的惯量仍主要由常规电源提供。因此，为了简化分析，针对算例系统作如下假设。1）负荷仅由新能源发电与常规电源供电，且新能源发电不提供参与调频。当新能源出力占比为负荷的n%时，剩余的负荷由常规电源出力承担。其中，水力发电与火力发电分别占常规电源发电的44%与56%。2）系统常规电源的等效惯性时间常数按两种情况考虑，即Teq0分别为10 s 和15 s。随着新能源出力占比增加，按照等容量替代同步机组的方式考虑，系统等效惯量Teq与新能源出力占比的关系为Teq=Teq0×(1-n%)(s)。

3）对于频率跌落最低值fNadir的约束，为了避免频率变化过程触及低频减载动作门槛值，系统的fNadir不得低于低频减载动作起动整定值fUFLS的典型值，即49 Hz。对于频率变化率ΔfRoCoF的约束，为了避免同步机产生滑极现象而损毁内部结构，考虑常规机组对ΔfRoCoF的耐受能力后，文献［24-25］建议系统的ΔfRoCoF不得超过2 Hz/s。为了对比频率约束对新能源承载能力的影响，算例同时考虑了频率稳定约束取fNadir＞49.1 Hz 与Rmax＜0.4 Hz/s 的情况。

3.1.2 评估结果

采用上述基于频率响应模型的电网新能源承载能力评估方法，计算算例系统的频率稳定域如图7所示。

图7 算例系统的频率稳定区域Fig.7 Stability domain of the frequency of the example system

结合图7 所示结果，表1 给出了不同系统惯性时间常数、不平衡功率扰动以及频率约束条件下电网新能源承载能力评估结果。

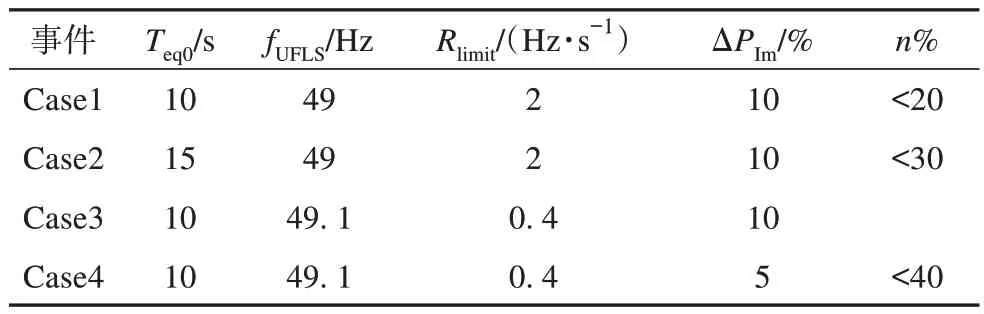
表1 电网新能源承载能力算例评估结果Tab.1 Assessment results of renewable energy power generation maximum penetration of power grid

当系统惯性时间常数Teq0为10 s，频率约束fNadir＞49 Hz，Rmax＜2 Hz/s 时，仅靠常规电源的调频能力则新能源发电比例承载占比不能超过20%。若系统等效惯性时间常数Teq0由10 s 提升至15 s，同样的频率约束条件下，在10%功率缺额情况下的最大新能源发电承载比例提升至30%。

另一方面，当采用更严苛的频率稳定约束时（fNadir＞49.1 Hz，Rmax＜0.4Hz/s），频率稳定区域缩小，在10%不平衡功率扰动下系统的新能源承载能力严重受限。如果降低对电网承受扰动的要求，比如按照5%不平衡功率扰动考核，同样的约束条件下电网新能源承载能力可以达到40%。

3.1.3 时域仿真验证

基于图2 所示3 机9 节点系统，建立含风电和同步机组的全系统详细电磁暂态仿真模型，通过对不平衡功率扰动下系统频率变化的过程进行仿真验证。其中，系统总有功负荷设定为900 MW，并根据表1 的Case1、Case2 与Case4 设置3 种场景，新能源发电占比按最大承载占比给定。在t=20 s 时，使稳定运行的系统突增有功负荷，遭受不平衡有功扰动，分别观察Case1、Case2 与Case4 三种场景下系统的频率变化曲线以及常规电源与新能源发电的调频出力，如图8—9所示。

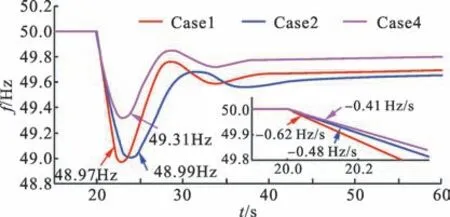
图8 算例系统的频率变化曲线Fig.8 Frequency waveforms of the example system

图9 常规电源与新能源的调频出力Fig.9 Regulation power from conventional power generation and renewable energy power generation

由仿真结果可知，在10%不平衡功率扰动下，Teq0=10 s 且新能源占比为20%的算例系统与Teq0=15 s 且新能源占比为30%的算例系统的最大频率变化率均小于2 Hz/s，而其系统频率分别跌落至48.97 Hz 与48.99 Hz，均处于频率稳定约束（fNadir＞49 Hz，Rmax＜2 Hz/s）内fNadir指标约束的临界点，说明在相同的频率稳定约束下，Teq0=15 s 时算例系统的新能源承载能力更高。但是Teq0=10 s 时算例系统在20%新能源占比下遭受10%功率缺额后，系统的频率指标均无法满足fNadir＞49.1 Hz 与Rmax＜0.4 Hz/s 的稳定约束，说明该约束下按10%不平衡功率扰动考虑的系统最大新能源承载占比低于20%，严苛的频率稳定约束将制约电网的新能源承载能力。而降低不平衡扰动功率至5%后，Teq0=10 s 且新能源占比为40%的算例系统的fNadir与Rmax分别为49.31 Hz 与0.41 Hz/s，处于频率稳定约束（fNadir＞49.1 Hz，Rmax＜0.4 Hz/s）内Rmax指标约束的临界值附近，说明系统的新能源承载能力可以达到40%。仿真结果与理论分析相对应。

3.2 新型新能源发电技术提升系统频率稳定性研究

新能源发电单元辅助调频有两种方式，一种是基于现有的电流矢量控制方式，即跟网型控制方式，其在外环附加频率及其变化率反馈控制，实现一次调频和虚拟惯量控制；另一种是电压源型控制方式，即构网型控制方式，其控制方式自身具有自动响应电网频率变化的特点，因而可以实现主动等效惯性支撑，另一方面通过设置频率调差控制实现一次调频。本节应用所提电网新能源承载能力评估方法，对新能源辅助调频对电力系统新能源承载能力的提升作用开展研究。

3.2.1 跟网型/构网型机组辅助调频控制的作用

在3.1 节算例系统中，同步电源惯性时间常数为10 s，分别按照跟网型和构网型新能源机组频率控制等效模型，基于系统频率响应模型计算两种控制方式下的频率稳定域，如图10—11所示。

图10 新能源采用跟网型调频前后系统的频率稳定域Fig.10 Frequency stability domains before and after renewable energy generator adopts grid-following frequency regulation control

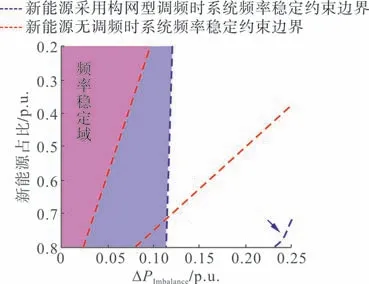
图11 新能源采用构网型调频前后系统的频率稳定域Fig.11 Frequency stability domains before and after renewable energy generator adopts grid-forming frequency regulation control

评估结果表明，相比于新能源无调频能力的场景，新能源机组采用跟网型调频控制可以使频率跌落最低值（fNadir）得到有效改善，但是对频率变化率（Rmax）几乎没有影响，这主要是跟网型机组的附加调频功率指令值依赖对电网频率的测量生成，对频率的测量将存在一定延时，限制了跟网型机组的惯量响应能力。给定10%不平衡功率扰动，全部新能源参与调频的情况下，考虑频率约束的电网新能源承载能力可达75%，主要受Rmax指标约束。

构网型调频控制能够同时抑制频率跌落最低值（fNadir），同时降低频率变化率（Rmax），算例结果表明新能源全部采用构网型控制，按照fNadir为49 Hz，Rmax小于-2 Hz/s考虑频率约束时，电网在80%新能源占比时，能够承受的最大不平衡功率扰动大小处于10%～15%系统负荷功率之间。

3.2.2 时域仿真验证

为了验证新型新能源发电技术对系统频率稳定性提升作用研究的有效性，在相同的算例条件下，构建新能源机组不参与调频以及进行过跟网型与构网型调频控制改造后的3 机9 节点系统（图2 所示），其中，新能源出力占比设为75%。在t=20 s 时，使稳定运行的系统突然出现10%有功功率缺额，对比新能源采取两种调频控制下与新能源无调频能力时的系统的频率变化曲线，如图12 所示。图13 给出了在两种调频控制下系统常规电源与新能源发电的调频出力的对比。

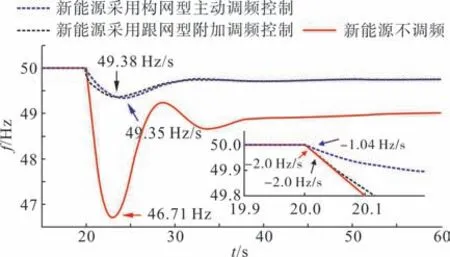
图12 新能源发电频率控制对系统频率稳定性的作用Fig.12 Effects of renewable energy power generation frequency control on system frequency stability

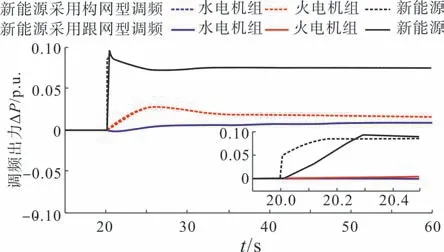
图13 常规电源与新能源的调频出力Fig.13 FM power from conventional power generation and renewable energy power generation

由仿真结果可知，新能源机组具备较常规机组更快的调频能力，与新能源机组无调频能力时相比，新能源调频有效抑制了系统的频率跌落深度，提升了系统的频率稳定性。对于最大频率变化率，跟网型调频控制下新能源基于频率测量响应系统频率变化，由于频率变化量测延时较大（0.2～0.5 s），在扰动瞬间无法为抑制频率变化提供支撑，因此，Rmax无明显改善。而构网型机组控制本身具备响应电网频率变化的能力，不存在频率检测延时，在有功功率缺额发生后能够提供等效惯量支撑，从而显著降低电网频率变化率。

需要说明的是，实现构网型控制有不同的方法，定量评估其对系统惯量的贡献是需要进一步研究的问题。本文所提供的构网型控制机组调频模型对应基于虚拟同步控制的方法，理论上其所提供惯量即为虚拟同步控制中的惯量参数Tj。计及构网型新能源机组提供的虚拟惯量后系统的等效惯量T'eq可以从式（1）推导得到：

式中：Tj、Sjn分别为系统内第j台构网型新能源机组的虚拟惯性时间常数以及额定容量；Sb为系统容量基值；GRES为构网型新能源机组的集合。

利用式（4）和频率响应模型对算例系统等效惯量及ΔfRoCoF进行估算，考虑构网型新能源机组提供的虚拟惯量后与新能源无调频能力时的系统的等效惯量分别为4.75 s与2.5 s，对应最大频率变化率分别为1.05 Hz/s 与2 Hz/s，与图12 所示详细电磁暂态仿真结果一致。必须指出，虚拟同步控制参数Tj的取值受到机组变流器直流电压变化允许范围和控制稳定性的约束，如何合理设计该参数也是需要进一步研究的问题。

3.3 基于10机39节点算例系统的应用验证

为了验证所提新能源承载能力评估方法对复杂多机电力系统的适用性，检验新能源辅助调频控制是否有效，选取IEEE 10机39节点标准算例，10台机组均为火电机组。

3.3.1 频率稳定域评估

算例系统无新能源时同步电源装机容量7 563 MVA，惯性时间常数为10 s，总有功负荷为4 002 MW。以负荷容量为容量基准，折算得到的系统惯性时间常数Teq为18.90 s。同步机出力水平按照0.52 p.u.设置，通过将部分同步电源替换为等容量、等出力水平的新能源机组来模拟新能源渗透率逐渐增高的场景。频率稳定约束条件为fNadir＞49 Hz，Rmax＜2 Hz/s。按照所提承载能力评估步骤，得到系统频率稳定域如图14所示。

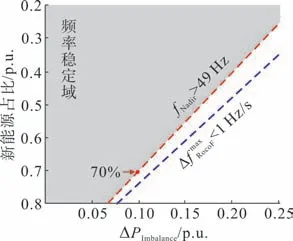
图14 系统的频率稳定域Fig.14 Frequency stability domain of the system

在fNadir＞49 Hz 与Rmax＜1 Hz/s 的频率稳定约束指标下，频率稳定域主要受到频率跌落最低值的限制。以不平衡功率10%为例，系统能够承载的最大新能源占比为70%，当新能源占比低于70%时，系统最大频率变化率和频率跌落最低值满足频率稳定指标约束条件。相比3 机9 节点算例各种新能源占比工况，10 机39 节点算例系统对应等效惯量高出近一倍，因此承载能力也相应较强。

3.3.2 时域仿真验证

在PSCAD/EMTDC 中建立算例系统电磁暂态仿真模型，验证上述评估结果的准确性。设置新能源出力占比70%，在仿真的第20 s于节点16突增有功负荷400.2 MW，即系统出现10%不平衡功率，分别记录算例系统在频率响应模型下与电磁暂态仿真中的暂态频率响应曲线，如图15（b）所示。

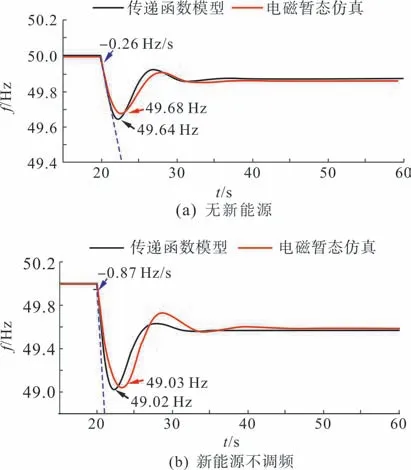
图15 仿真模型与传递函数模型的系统频率响应波形Fig.15 System frequency response of simulation model and transfer function model

仿真结果表明，有功功率发生突变后，频率响应波形最大频率变化率（0.87 Hz/s）满足频率稳定约束条件（＜1 Hz/s），但是频率跌落最低值（49.03 Hz）近似达到约束指标阈值（49 Hz），可见在10%的不平衡功率条件下，系统恰好能够承载70%的新能源，与承载能力模型评估结果相符。时域仿真频率跌落最低值（49.03 Hz）和最大频率变化率（0.87 Hz/s）与理论计算结果（49.02 Hz、0.87 Hz/s）基本相等，表明所提承载能力评估模型的准确性能够在10机39节点的系统上得到验证。

与图15（a）无新能源场景对比，新能源取代部分同步机使得系统频率响应指标明显恶化，初始频率变化率增加，频率跌落深度增加。

3.3.3 稳定性提升技术评估

新能源替代同步机可能对系统频率稳定性造成不利影响。为了缓解频率稳定性降低的问题，采用上文提出的新能源发电单元辅助调频技术，通过跟网型或构网型主动调频控制改善频率响应特性。

图16 给出的是新能源采用跟网型调频控制和构网型调频控制的系统频率稳定域。其中跟网型与构网型新能源的虚拟惯量系数相等，一次调频系数相等。

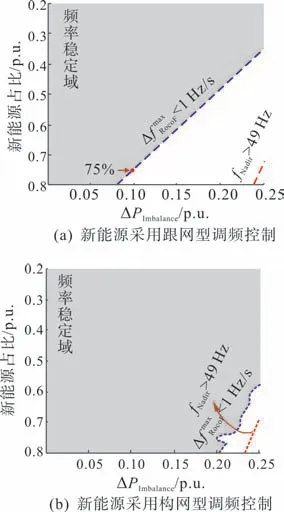
图16 系统的频率稳定域Fig.16 Frequency stability domain of the system

结果显示，新能源机组采用跟网型调频控制或构网型调频控制均能有效扩大频率稳定域范围。采用跟网型调频控制使得频率跌落最低值得到改善，最大频率变化率边界几乎保持不变，稳定边界由原先拓展至最大频率变化率指标曲线处，10%不平衡功率下系统允许最大新能源占比增加至75%。采用构网型调频控制技术则能够同时改善频率变化率和频率跌落最低情况，10%不平衡功率下系统允许最大新能源占比增加至80%以上。

图17 对比了10%的不平衡功率、70%的新能源出力占比下，新能源采用两种主动调频控制，基于传递函数模型和电磁暂态仿真的频率响应波形。可以看到，两者频率暂态跌落和恢复过程是吻合的，表明了本文所提模型方法的有效性。

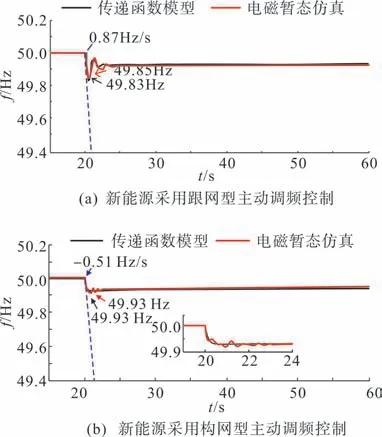
图17 仿真模型与传递函数模型的系统频率响应波形Fig.17 System frequency response waveforms of simulation model and transfer function model

跟网型对频率响应的改善作用局限于频率跌落最低值的改善，不能提升系统惯量，频率跌落速率基本与无调频控制时相等。图17（a）所示频率恢复过程中存在较为明显的振荡，这是由于系统低惯性所导致。

与之相比，构网型调频能够提高系统等效惯量，改善初始频率变化率，图17（b）响应波形甚至呈现过阻尼特征，图18 中同步机功角摇摆幅度也小于跟网型场景，相较于跟网型调频控制具有更为理想的频率响应特性。

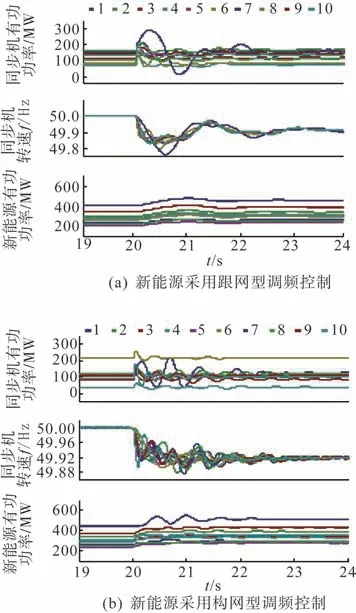
图18 各台机组的时域仿真波形Fig 18 Time domain simulation waveforms of each unit

图18 给出了采用跟网型和构网型调频控制的系统在10%不平衡功率的冲击下，同步机有功功率、频率以及新能源有功功率响应波形，也可以看出构网型风电控制辅助调频时，同步电机功率转速摇摆幅度明显小于跟网型风电控制参与调频的情况。

需要说明的是，图17（b）中电磁暂态仿真在频率跌落过程中出现的振荡，是构网型控制的固有低频控制模式，与频率动态无关。

可见，新能源主动频率支撑技术提升较大规模电力系统的频率稳定性具有积极意义，采用构网型调频技术相较于跟网型调频具有一定优越性。

针对以上10 机39 节点系统的上述算例结果证明了本文提出的新能源承载能力评估方法的有效性。

4 结论

以新能源为主体的新型电力系统中，电网新能源承载能力是必须研究的课题。本文从频率稳定的角度研究了基于系统频率响应特性模型的电网新能源承载能力评估方法，并结合算例开展应用研究，主要结论如下。

1）基于调频资源频率控制响应特性构建系统的频率响应模型可以方便地接入电网不同类型调频资源，用于评估电网频率动态特性，建模简便有效。

2）考虑频率跌落最低值和频率变化率约束基于系统频率响应模型构建的频率稳定域可以对电网新能源承载能力进行有效评估，详细时域仿真验证了其有效性。

3）新能源发电单元频率控制能够显著提升电网新能源承载能力。现有跟网型控制附加频率控制存在电网频率检测延时，提供的惯量有限，而构网型控制自身能够响应电网频率变化，起到降低频率变化率的作用。仿真表明两种控制方式在抑制频率跌落最低值方面的作用基本相同。

本文提出的基于系统频率响应模型评估电网新能源承载能力的方法，将全系统按照等值单母线系统来考虑，可以适应不同负荷水平的电网规划分析阶段的新能源承载能力评估应用，还可以进一步用于电网不同响应特性调频资源容量需求评估，比如适应新型电力系统频率控制的快速频率响应资源需求等。但是，对于大容量互联同步电网具有网内输电通道约束的情况，需要结合电网结构建立分区域互联的系统频率响应模型，这方面的工作有待进一步开展研究。