基于融合嵌入向量的多目标优化社区发现

韩存鸽, 陈展鸿, 郭 昆*

(1.武夷学院 数学与计算机学院 福建省茶产业大数据应用与智能化重点实验室, 福建 武夷山 354300; 2.福州大学 计算机与大数据学院, 福建 福州 350108)

0 引言

现实世界中的许多复杂系统都可以建模为网络,如生物网络、社交网络、科学合作网络等.在这些网络中,节点之间的连接关系非常复杂,节点的度、聚集系数、连通性等属性也各不相同.社区发现[1]是复杂网络研究中的一个重要领域,其主要目的是发现网络中的社区结构.社区发现可以从节点属性角度进行分类,分为无属性网络和属性网络的社区发现.在过去,许多社区发现算法仅考虑网络结构,忽略了节点间的属性信息.然而,现实世界中许多网络都具有属性,如社交网络中的个人资料信息、科学合作网络中的学科领域等.

基于进化计算的社区发现早期应用于无属性网络.2008年,Pizzuti[2]首次提出了GA-Net,该算法采用邻位编码的遗传算法搜索社区,是最早的基于进化的社区发现方法.随后,一些基于多目标优化的进化算法被应用于社区发现.2009年,Pizzuti[3]提出了基于多目标优化的进化计算社区发现算法MOGA-Net,算法通过优化社区得分和社区适应度来完成无属性网络上的社区发现.2013年,Gong等[4]提出的MODPSO结合粒子群算法,对核k均值(KKM)和比率割(RC)这两个目标进行优化,提高了社区发现的精度.2018年,Zhang等[5]提出了一种在大规模图上进化计算进行社区发现的算法RMOEA,采用了一种节点规约策略来将同社区的节点合并成一个超级节点进行迭代,提高了算法的收敛速度与精度.此后,一些基于属性网络的社区发现算法被相继提出.2017年,Li等[6]提出了MOEA-SA的多目标优化社区检测算法,通过优化模块度和属性相似性来进行社区发现,使得社区内的节点间的边密集并且属性相似,提高了社区划分的正确性.2019年,Pizzuti等[7]提出了MOGA-@Net算法,它尝试对多种目标函数进行优化,并通过合并社区的方式来提高社区发现的精度.2021年,Sun等[8]提出了CE-MOEA,其利用图神经网络对网络的边进行编码,每条边都对应着一个连续变量,最后通过边的非线性变换来生成社区划分.

目前,基于属性网络多目标优化进化社区发现算法(MOEAs)主要面临两个挑战:(1)编码方式都直接或间接使用邻接编码策略,使得算法的搜索能力易受网络结构限制,社区划分的质量不高;(2)进化算法容易陷入局部最优,导致社区发现的精度不高.

针对以上问题,本文提出一种基于融合嵌入向量的多目标优化社区发现算法FEV-MOEA(Fusion Embedding Vector MOEA),首先,设计一种基于融合系数的编解码方案,通过利用每个节点的属性与结构嵌入向量,以克服算法对网络结构的限制,提高社区划分质量.其次,提出一种后处理节点修正策略,通过该策略对社区划分结果进行修正,提高社区划分的精度.主要创新点如下:

(1)通过设计融合系数编解码方案,充分利用节点属性、结构嵌入向量.编码时,采用连续值编码方式,将每个节点编码成一个基因位,每个基因值表示该节点结构、属性嵌入向量的融合程度,避免了传统编码方案中丢失节点间连续信息的问题.解码时,根据融合嵌入向量结合聚类算法,使得解码方式不受网络结构的限制,以提升社区发现的质量.

(2)通过设计后处理节点修正策略,不断优化新社区的模块度与社区内属性相似度,使得算法的解能够克服陷入局部最优的问题,提高社区发现的精度.

(3)通过在真实和人工数据集上实验,验证了FEV-MOEA算法能够有效提高社区发现的精度.

1 FEV-MOEA算法

1.1 基本概念

定义1复杂网络:复杂网络可以被建模三元组G=(V,E,A),其中V={v1,v2,…,vn}表示节点集合,n代表网络节点数.E={(vi,vj)|vi,vj∈V,i≠j},表示网络边的集合,A=[a1,a2,…,an]T∈R|v|×m表示节点的属性矩阵.

定义2节点嵌入向量:节点嵌入向量是指将网络中的每个节点表示为一个低维的实数向量,它们可以将节点间的拓扑与属性结构信息转换为低维向量空间中的向量,从而可以在向量空间中进行节点的聚类操作.

定义3模块度Q:模块度Q是复杂网络中用于衡量社区结构的一种指标,通常用符号Q表示.它衡量了某种分割方式下,网络中的节点分配到社区的紧密程度与该分割方式随机下产生的网络中的节点分配到社区的紧密程度之差.

(1)

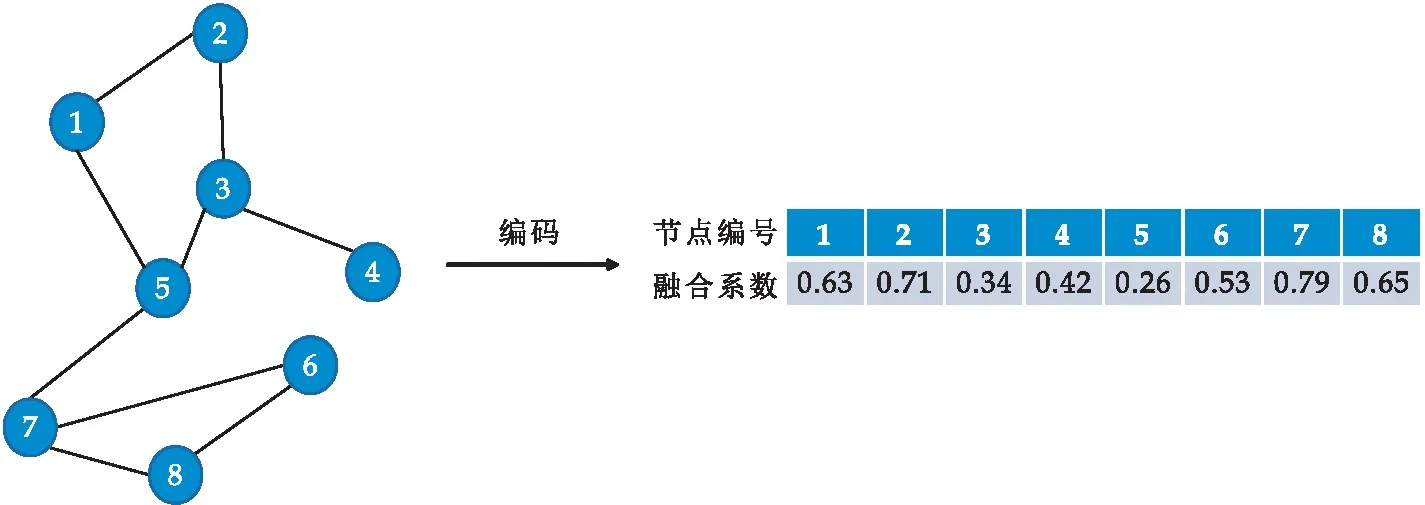
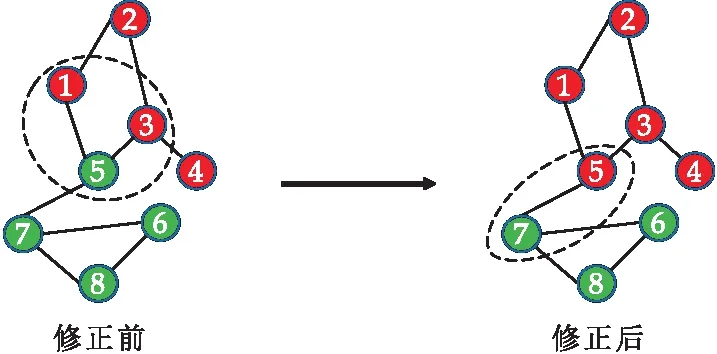
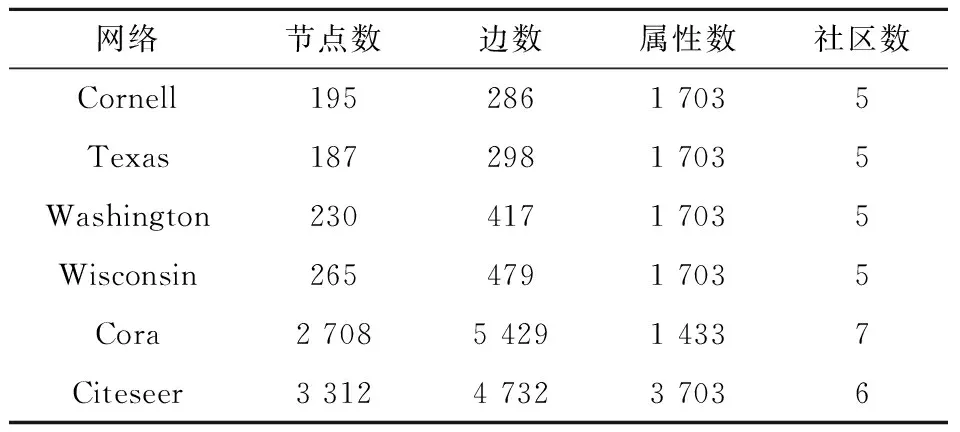
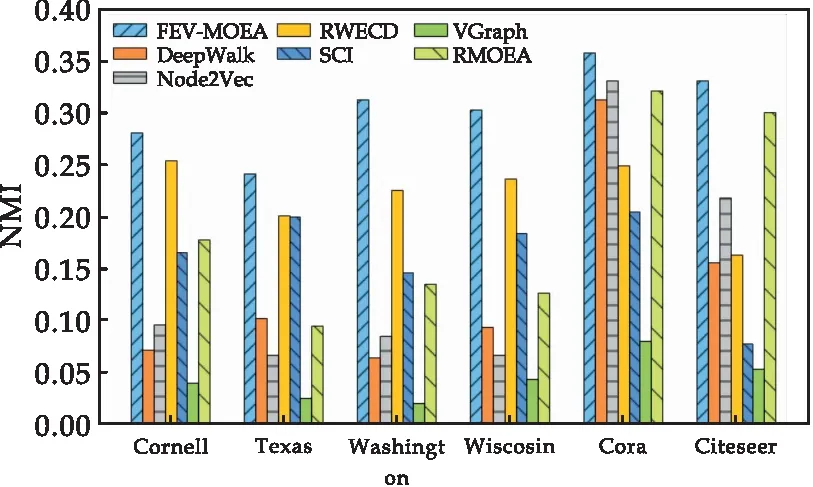
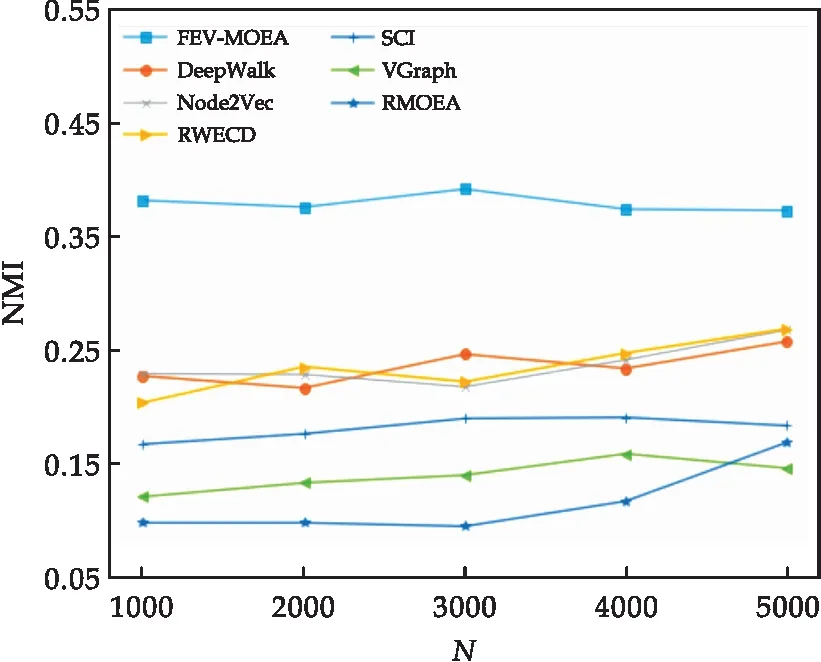
式(1)中:1=

定义4节点属性相似度s(i,j):节点属性相似度用来刻画两个节点关于属性上的相似情况,两个节点越相似,则两节点的属性相似度越高.

s(i,j)定义为:

(2)

定义5社区内属性相似度SA.社区内属性相似度SA是社区发现中用于衡量在属性上划分社区的质量.当同一个社区内的节点属性越相似,则社区内属性相似度SA越高.

(3)

式(3)中:c是划分社区的总数,ck表示第k个社区的节点集合,s(i,j)定义节点间的属性相似度,rk为第k个社区的节点个数.

多目标优化:多目标优化研究如何在具有多个目标的优化问题中找到一组最优解.在传统的单目标优化问题中,目标函数单一,优化目标是最小化或最大化一个特定的目标.而在多目标优化问题中,存在多个目标函数,无法简单地将它们归纳为单一目标函数.在多目标优化理论中,存在解支配关系.在两解x,y中,如果x在所有目标上优于y,则称解x支配解y,x为非支配解.支配关系表示解之间的优劣关系.而帕累托解集是一组非支配解的集合,表示了多目标优化问题的最优解的信息,多目标优化算法旨在搜索并逼近帕累托解集.在基于多目标的属性网络社区发现中,研究重点在于如何利用蕴含在节点中的属性信息以及节点间的结构关系,去检测潜在的社区:(1)在结构上,检测出的社区内部节点的边较为密集,而社区间节点的边较为稀疏;(2)在属性上,同一个社区内部的节点属性相似度较高.因此基于多目标优化的属性网络社区发现问题可以建模为:min{Q,SA}.

1.2 FEV-MOEA算法框架

FEV-MOEA 的算法框架如图1所示,由三个阶段构成,分别为图增强、嵌入向量生成以及个体初始化阶段、种群与帕累托前沿的更新阶段、以及后处理修正阶段.在阶段一中,首先,将原始图根据属性信息构造增强图,使得图上的属性信息更加丰富.接着,利用DeepWalk分别获得结构、属性上的嵌入向量.最后,根据嵌入向量初始化个体.阶段二将个体进行交叉、变异与选择操作来更新种群在解空间搜寻优秀个体.阶段三将帕累托解集进行后处理修正,使得可行解能够避免陷入局部最优的问题.

图1 FEV-MOEA算法框架

1.3 图增强、嵌入向量生成及种群初始化

1.3.1 图增强

图2表示k=2时,节点5的图增强示意图.

图2 图增强示意图

在属性网络中,存在着一类结构与属性信息不一致的社区,即在社区内的节点在结构上并没有明显的社区边界,甚至出现隶属于同一个社区的节点在不同的连通分支,但它们的属性相类似.这种结构与属性信息不一致的网络会导致算法精度降低,为了更好地识别节点之间的潜在关系,需要根据节点间的属性对原始图结构进行增强,通过增强的图结构,可以更准确地识别节点之间的社区,从而更好地理解复杂系统中节点之间的相互作用.具体图增强策略如下:对于每个节点V,计算出前k个与其节点属性相似度最大的节点集合,将V与节点集合里的每个节点新增一条边完成图增强.

1.3.2 嵌入向量生成

FEV-MOEA解码时需要结合结构、属性嵌入向量得到最终的社区划分,因此需要生成对应的结构、属性嵌入向量用于后续个体的解码.FEV-MOEA采用DeepWalk[9]算法分别生成结构、属性嵌入向量.DeepWalk是一种基于随机游走的网络嵌入方法,用于将节点映射到低维向量空间中,它通过捕捉节点在网络中的局部邻域来捕捉节点的相似性,并将其表示为低维向量,DeepWalk由随机游走与Skip-gram模型两个关键步骤组成,随机游走生成了大量的遍历序列,而Skip-gram模型将这些序列看作自然语言中的句子,并通过最大化预测周围节点出现概率的目标函数来学习节点向量表示.图3展示了结构嵌入向量与属性嵌入向量的生成例子.针对结构嵌入向量初始化,游走序列采取原始图上的随机游走,而针对属性嵌入向量初始化,游走序列采取增强图上的随机游走.

图3 结合DeepWalk生成嵌入向量

1.3.3 种群初始化

在进化计算的社区发现算法中,传统的编码方案分基于节点标签的编码方案(Label-based)与基于邻居节点的编码方案(Locus-based)两种.Label-based编码将每个节点编码成一个基因位,每个基因位的值表示节点所属的社区,解码时每个基因的值就代表着该节点隶属的社区.该编码方案需要将编码进行离散化编码,会丢失节点之间的连续性信息,可能会导致进化失去部分信息.

而Locus-based是将每个节点编码成一个基因位,每个基因位的值标识该节点的某个邻居节点的编号,解码时将该节点与其基因值对应的邻居节点划分为同一个社区.现有编码方案难以克服局部最优,比如,若一个节点在进化过程中被分配到一个错误的标签时,其周围的节点也可能被分配到相同的错误标签,可能会导致算法陷入局部最优,同时因受到网络结构的影响,划分社区的节点必须在同一个连通分支.

在FEV-MOEA中,设计一个基于融合系数的编码及解码方案,图4为基于融合系数的编码示意图.如图4所示,增强图共有8个节点,编码时将每个节点编码成一个基因位,每个基因值代表着该节点关于结构、属性嵌入向量的融合程度,具体基因值的初始化详见InitialPopu伪代码.图5为基于融合系数的解码示意图,其中,gen(i)表示i节点对应的融合系数,Si表示i节点的结构嵌入向量,Ai表示i节点的属性嵌入向量.结合Si与Ai,可以通过公式gen(i)*Si+(1-gen(i))*Ai计算加权后节点i的融合嵌入向量Fi.当节点1的结构嵌入向量S1为[40,50],属性嵌入向量A1为[80,60]时,则融合嵌入向量F1=0.63*[40,50]+0.37*[80,60]=[55,54].计算所有节点的融合嵌入向量F后,结合Kmeans[10]聚类算法得到最终的社区划分.

图4 基于融合系数的编码方案

图5 基于融合系数的解码示例

1.4 种群更新

种群初始化后需要经过多次选择、交叉与变异算子使得种群逼近全局最优解.为了适配提出的基于融合系数的编码方案,本文的选择算子为锦标赛选择算子,锦标赛选择算子是一种常用的选择算子,其思想是随机选择一定数量的个体作为竞争者,从中随机选择若干个非支配解,作为下一代的子种群的父代.而交叉算子采取模拟二进制交叉,模拟二进制交叉是一种常用的交叉算子,其主要过程是先选择俩个父代个体,再对于每对等位基因确定其交叉概率和分布指数,计算最终交叉的中间变量得到子代交叉后的基因值.而变异算子采用多项式变异,多项式变异可以用于连续值编码的变异操作,增加搜索空间的探索能力,其主要思想是对于每一个基因,计算其变异区间,再根据变异区间的范围对基因值进行变异操作,变异区间的大小会受到变异概率的影响.父种群经过多次的选择、交叉与变异操作后得到子种群,接着通过父、子种群的目标函数值选出帕累托解集,从帕累托解集中选择若干个个体参与下轮种群的更新迭代,直至迭代次数达到最大次数.

1.5 后处理节点修正

复杂网络结构与属性的复杂性和规模会影响算法的效果,当社交网络结构较为复杂时,算法容易出现局部最优解.为避免算法陷入局部最优,提出一种基于目标函数最优的节点修正策略,策略将帕累托解集中的边缘节点所属社区进行修正,使得修正后的社区划分结果具有更高的模块度Q与社区内属性相似度SA,以克服局部最优的问题,提高社区划分的精度.

在后处理节点修正方案中,首先,计算出社区划分的目标函数模块度Q1与社区内属性相似度SA1.其次,找到与其他社区有连接边的节点, 称之为边缘节点.接着,将这些边缘节点尝试加入到相邻社区,重新计算目标函数模块度Q2与社区内属性相似度SA2.最后,当Q2>Q1且SA2>SA1时,则将这些边缘节点加入到相邻社区,否则不加入.图6为后处理修正的例子,其中修正前节点1、3、5为边缘节点,当边缘节点1和3尝试加入到相邻社区时,模块度Q与社区内属性相似度SA并不会提高,因此边缘节点1和3的社区标签并不进行修正,而边缘节点5尝试加入到相邻社区时,模块度Q与社区内属性相似度SA都会提高,因此将边缘节点5加入到邻近社区,社区标签进行修正.修正后,边缘节点为5、7,而节点5、7尝试加入到邻近社区都不会使模块度Q与社区内属性相似度SA提高,后处理修正结束.

图6 后处理修正

1.6 算法伪代码

FEV-MOEA算法基于NSGA-II进化框架进行实现.(Non-dominated Sorting Genetic Algorithm II,NSGA-II):NSGA-II是一种常用的多目标进化计算方法,它是基于遗传算法的一种扩展,能够同时优化多个目标函数.以下是FEV-MOEA的算法伪代码:

FEV-MOEA算法伪代码输入:G=(V,E,A); // 属性网络图增强条数k;种群规模n;最大迭代次数T;交叉概率pc;变异概率pm;输出:社区划分集合 C// 阶段一 图增强、嵌入向量生成以及种群初始化1.t=1;2.G'←enhance(G,k) //根据1.3节对原始图G进行增强,生成增强图G'3.SV←DeepWalk(G) //根据原始图G利用DeepWalk算法生成结构嵌入向量SV4.AV←DeepWalk(G') //根据增强图G'利用DeepWalk算法生成属性嵌入向量AV5.Pt←InitialPopu() //进行种群的初始化// 阶段二 种群更新6.While t < T do7.Set Qt={}//子种群Qt8.While |Qt| < n do9.X1,X2←TournamentSelection(Pt); //竞标赛选择10.X1,X2←SBX(X1,X2,pc); //模拟二进制交叉11.X1,X2←PolynomialMutate(X1,X2,pm); //多项式变异12.Qt=Qt∪{X1,X2};13.End 14.Pt+1=Pt∪Qt //将子种群和父种群融合15.F=(Q(Pt+1),SA(Pt+1)) //Fc 计算子代的目标函数值16.PS←ParetoSet(Pt+1,F) // 根据目标函数值F获得帕累托解集17.Pt+1←SelectN(PS,n); // 选择前n个非支配解集进行下一代种群的更新18.t=t+119.End // 阶段三 帕累托解集的后处理得到社区划分集合C20.Set C={}//社区划分结果 21.For ind in PS:22.com=decode(ind,SV,AV); //根据1.5节对个体进行解码获得社区划分com23.com=PostProcess(com); // 根据1.6节对个体进行后处理修正24.C=C ∪ com25.Return C

enhance( )函数对原始图进行增强,伪代码如下:

enhance()函数伪代码输入:G=(V,E,A); // 属性网络原始图,图增强条数 k;输出:增强图G' 1. G'=G 2. For i=1 to |N| do:3. sim=[] //节点i的属性相似度列表4. For j=1 to |N| do:5. sim .add(s(i,j) ) // 节点属性相似度s(i,j)6. similar_nodes=sort(sim) //根据属性相似度降序排序,得到对应的节点列表7. For n in similar_nodes:8. G'.addEdge(i,n) //添加一条从节点i到相似节点n的边 Return G'

InitialPopu( )函数用于种群初始化,其伪代码为:

InitialPopu算法伪代码输入:G=(V,E,A); // 属性网络,种群规模 n;输出:P //初始种群1.P={}2.For k=1 to n do:3. For i=1 to |N| do:4. Xk(gen(i))=1-s(i,j) //第k个个体节点i的融合系数 5. P←Xk6.Return P

2 实验结果与分析

为了验证FEV-MOEA算法的性能,本文选择6个对比算法在真实数据集与人工数据集进行实验.其中,DeepWalk与Node2Vec[11]是基于随机游走的算法, SCI[12]与VGraph[13]是基于模型的算法,而RMOEA[5]与RWECD[14]是基于进化计算的算法.所有对比算法的参数都与原论文保持一致.

2.1 实验数据集

2.1.1 真实网络数据集

表1给出了以上6个真实网络的具体参数信息.

表1 真实网络参数

在真实网络数据集实验上,本文选择了6个数据集进行实验以验证FEV-MOEA算法的有效性,分别包含:WebKB[15]中四个美国大学的计算机交流网络Cornell、Texas、Washington、Wisconsin与两个科学引用网络Cora[16]、Citeseer[16].

2.1.2 人工网络数据集

实验采用LFR[17]网络生成工具生成只包含结构信息的人工网络,利用文献[18]的方案为每个节点生成对应的属性信息.两组具有不同参数设置的人工网络D1、D2用于验证算法的有效性,具体参数及设置如表2所示,其余未说明的参数设置为LFR工具的默认值.D1网络侧重于实验不同的μ值对算法精度的影响,μ值代表社区的混合程度,μ值越大,则社区结构越模糊,算法越难划分出正确的社区.而D2网络侧重于实验不同网络规模变化对算法精度的影响,N值越大,则网络规模越大.

表2 人工网络D1、D2的参数设置

2.2 评价指标

采用标准互信息NMI[19]与平衡分数F1[20]

对算法的结果进行评价.NMI定义如下:

(4)

NMI度量两个聚类结果相似程度的指标,其值在 [0,1] 之间,数值越大表示聚类结果越相似.其中,CA、CB分别表示真实社区划分与预测的社区划分结果;Nij表示同时被分配到CA中第i个社区与CB中第j个社区的节点数量,Ni表示CA中第i个社区的节点数量,Nj表示CB中第j个社区的节点数量.

F1 用于衡量算法精确性和召回率的指标,F1定义如下:

(5)

(6)

(7)

式(7)中:F1值在 [0,1]之间,数值越大表示算法性能越好.TP表示在同一真实社区的节点被划分到相同社区的节点对个数,TN表示在不同真实社区的节点被划分到不同社区的节点对个数,FP表示在不同真实社区的节点被划分到相同社区的节点对个数,FN表示在相同真实社区的节点被划分到不同社区的节点对个数.

2.3 真实网络数据集实验结果

图7、图8分别为FEV-MOEA与其它6种对比算法在不同真实网络数据集下的精度实验,其中图7为NMI精度实验,图8为F1精度实验.实验结果表明,FEV-MOEA在各个真实网络数据集上的精度效果最佳,说明FEV-MOEA算法相较于传统的社区发现算法在属性网络社区发现上具有更好的精度,这是因为FEV-MOEA算法的编码方案能够有效提取每个节点的属性与结构信息,并通过后处理修正的策略,提高社区发现的精度.其中,DeepWalk、Node2Vec、RMOEA与VGraph算法只考虑了结构信息,因此在各个数据集上的效果不佳.而SCI与RWECD算法虽然考虑了属性信息,但是没有考虑到网络中可能存在着属性信息与结构信息不匹配的问题,因此虽然精度有所提升,但是也没有达到较高的精度.

图7 真实网络数据集NMI实验

图8 真实网络数据集F1实验

2.4 人工网络数据集实验结果

图9显示了FEV-MOEA算法与其它6种对比算法在D1网络组上关于社区混合参数μ的精度实验.从图9可以看出,所有算法的NMI值都随着社区混合参数μ的增加而减少,这是因为社区混合参数μ值越大,说明社区结构越模糊,算法越难检测到正确的社区划分.FEV-MOEA算法的精度虽然随着μ值的增加而降低,但是相较于其它比较算法,其精度下降的较为平缓,这是因为即使在面对社区结构模糊的网络时,FEV-MOEA算法通过综合考虑网络中的属性信息来弥补结构信息的不足,进而提高社区划分的精度.

图9 不同混合参数μ的实验结果

图10、图11显示了FEV-MOEA算法与其它6种对比算法在D2网络组上的精度实验,其中图10为NMI精度实验,图11为F1精度实验.实验结果表明,在各个规模的数据集下,FEV-MOEA算法都保持着最高的精度.网络规模越大意味着网络的结构会更加复杂,而FEV-MOEA算法通过融合节点的属性信息与后处理修正策略,能够在不同规模的网络下保持良好的鲁棒性与准确性.

图10 人工网络数据集NMI实验

因此,FEV-MOEA算法随着网络规模的增加,其精度一直保持在较高的水平并且没有较大的波动.而其余6种对比算法随着网络规模的增加,精度波动的幅度较大,说明其鲁棒性较差,无法在不同规模网络下进行有效的社区发现.

3 结论

本文提出了一种基于融合嵌入向量的多目标优化社区发现算法FEV-MOEA.与传统编解码方案不同,该算法的编解码方案能够利用到每个节点的属性与结构嵌入向量,使得算法能够不受到网络结构的限制继而发现高质量的社区.同时,设计一个后处理社区修正的策略,使得算法的解能够克服陷入局部最优的问题,提高社区发现的精度.通过在真实网络和人工网络数据集上实验,验证了FEV-MOEA算法能够在复杂属性网络上进行高精度的社区发现.未来,在现有工作基础上,针对异构网络社区发现展开探索,将异构网络中不同类型的信息与进化计算相结合以检测高质量的社区.