沟槽结构对水润滑轴承润滑特性影响机制∗

汪 骥 于鹏法 李 瑞 刘玉君 刘 晓 高 立 李晨龙

（大连理工大学船舶工程学院 辽宁大连 116024）

船舶水润滑轴承是一种节能环保的滑动轴承，水泵、船尾管和水轮发动机主轴等。与传统滑动轴承不同的是，为了使进入开式水润滑轴承的泥沙颗粒快速排出，减少泥沙对于摩擦副间的磨损，同时为了更快地排出轴承在工作过程中产生的热量，需要在轴承内衬材料上开出沟槽结构。因此，沟槽结构对于水润滑轴承尤其是大型水润滑轴承来说不可或缺。

水润滑轴承发展至今，已开发了许多结构的沟槽类型。按照沟槽结构相对于轴承的大小可分为深沟槽结构和微沟槽结构。研究表明，形成流体动压润滑后，深沟槽结构的水润滑轴承其水膜压力在沟槽处不连续，使得压力在沟槽处降为表压为0。微沟槽是指沟槽结构参数远远小于深沟槽的沟槽，对于微沟槽来说，其在微沟槽内部会形成流体动压效应。

在微沟槽结构对水润滑轴承润滑性能影响的研究方面，学者们已经展开了大量的研究。SHINKARENKO等［1］研究了物体表面纹理对软弹流润滑性能的影响，指出微体之间的润滑剂会产生额外的挤压效应。GONG 等［2］建立了水润滑微槽轴承的弹性流体动力润滑（EHL）模型，并对模型进行了实验验证，研究了偏心率和轴承材料对微槽轴承润滑性能的影响。XIE等［3］通过建立二维模型，详细探讨了操作条件和结构参数对流体特征的影响，研究了矩形微腔体内的润滑机制及润滑性能随腔体结构的变化规律。SHI 等［4］建立了轴承弹流润滑的数学模型，并根据载荷增量法和有限差分法分析了水润滑橡胶轴承在小扰动条件下的动态特性。王家序等［5］对微沟槽形貌对水润滑轴承混合润滑特性的影响进行了研究，指出由于不同沟槽内水膜增压能力以及抽吸作用的不同引起了水润滑轴承混合润滑性能的差异。GAO 等［6］利用计算流体动力学分析了不同轴承尺寸下、不同转速下偏心率对水膜压力分布的影响，为设计高效水润滑滑动轴承的初始直径尺寸的选择提供了参考。TALA－ IGHIL 和FILLON［7］通过适当的表面纹理几何形状和轴承表面上正确的纹理分布，发现轴承性能的提高主要通过最小的膜厚度来实现，在一定程度上也是通过增加微观特征来实现提高润滑性能。解忠良、焦春晓等［8－9］从微观层面探究粗糙峰与轴承润滑状态转变之间的关系，进而提出判断润滑状态转变的微观尺度标准。

对于深沟槽轴承，多位学者也深入探讨了沟槽结构对轴承润滑性能的影响［10－15］。杨利涛［16］通过建立圆弧型沟槽模型，分析了不同工况及轴承结构下的轴承润滑性能，发现沟槽处水压会出现降低的情况。王楠等人［17］利用有限元软件，研究了考虑轴瓦变形后的八沟槽水润滑橡胶轴承在不同偏心率和转速下的水膜压力分布，发现沟槽对水膜压力影响较大。刘宇等人［18］对轴向开槽水润滑径向轴承的润滑性能进行数值计算与分析，结果表明：轴向开槽轴承压力分布不连续，水槽处压力降低为0；轴承开槽后承载能力降低，槽的宽度越大，个数越多，轴承的承载能力越小。WANG 等［19］以实验的方式揭示了全尺寸WSB 的压力偏差和双向轴倾斜现象，系统地研究了偏心率、轴倾角和轴承结构参数对润滑和动态特性的影响，证实了沟槽结构对船用水润滑艉轴承的运行性能有很大的影响。

基于以上研究内容可以发现，相比于深沟槽结构，水润滑轴承的微沟槽结构可以提高轴承的承载能力和局部水压，改善轴承的润滑性能。然而，不同沟槽尺寸对水润滑轴承润滑特性的差异性影响，目前的研究还难以从原理上去解释。因此，本文作者以简化后的椭圆形沟槽为研究对象，提出了采用深深比（轴承间隙与沟槽深度的比值）、宽深比（沟槽宽度与沟槽深度的比值）等参数来表征水润滑轴承的沟槽结构，通过数值仿真得到沟槽内部的压力轮廓，研究了结构参数对水润滑轴承沟槽内部流体流动特征的影响，分析了沟槽结构参数对水润滑轴承摩擦因数的影响和轴承的润滑机制。文中通过CFD 方法从微观和宏观层面揭示沟槽结构对船用水润滑轴承润滑特性影响机制，为水润滑轴承优化设计提供了参考。

1 分析模型

1.1 流体动力学的控制方程

1.1.1 连续性方程

在水润滑轴承中，轴承内液体的流动遵循质量守恒定律，即在单位时间里流入微元的净质量，等于微元体内质量的增加率。对其内部的流体作连续性假设，假定微沟槽内的流体是不可压缩的、等热和等黏流体，满足Navier－Stokes（N－S）方程的要求。由此可推导出连续性方程（即质量守恒方程）的微分表达式为

式中：ρ是密度；t是时间；ux、uy、uz是速度矢量u的x、y、z分量。

式（3）即为水润滑轴承适用的连续性方程。

1.1.2 动量守恒方程

动量守恒定律表现为在单位时间里，作用于微元体上的各外力之和，等于流体动量的变化率。由此可导出动量守恒方程，即运动方程，又称作N－S 方程，完整形式如下所示：

式中：Fi是微元体上的重力等体力；p是流体微元体上的压力；τii、τij（i，j＝x、y、z）是微元体表面上黏性应力的分量。

对牛顿流体，有如下关系式：

式中：λ为第二黏度，取λ＝－2／3；μ为动力黏度。

将式（5）代入式（4），得到动量守恒方程：

式中：Si（i＝x、y、z）为方程的广义源项；grad（ui）＝∂ui／∂x＋∂ui／∂y＋∂ui／∂z（i＝1、2、3）。

1.2 流动状态

轴承在运转过程中尤其是在高速旋转过程中，其内部液体很容易进入湍流状态。对于水润滑轴承，由于水的黏度较低，很容易使流体的流动状态由层流变为湍流。判断流体流动状态通常用特征量雷诺数Re表征。对于水润滑轴承，雷诺数定义为以下公式：

式中：ρ是流体密度；v是表面线速度；A是过流断面截面积；η是流体的动力黏度；x是固体与流体在过流断面上接触的湿周长。

通常认为当雷诺数超过临界雷诺数时，流体流动状态便由层流状态变为湍流状态。对于水润滑轴承，出现湍流的临界雷诺数Rec为

式中：R为轴颈半径；c为轴承间隙。

1.3 空化模型

由于水的汽化压力很低，恒定温度下，液体压力降至低于饱和蒸汽压时，液体破裂，或溶有的微小空气泡、气核，在降压下长大且形成气穴，产生空化现象，其实质是气液两相之间的传质相变。在水润滑系统中很容易产生空化现象。空化过程中液相与气相的质量传递由以下方程控制：

式中：αv为气相体积分数；ρv为气体密度；Rg和Rc表示空化过程中液相和气相之间的质量传递。

1.4 轴承摩擦因数

依据以上方程可以求得轴承内水膜的压力分布，对压力进行积分可以得到轴承在x和y方向上的承载力Fe和Fθ为

水润滑轴承总的承载力为

假设橡胶轴瓦内表面的摩擦力全部由流体内部的黏性剪切流引起，对水润滑轴承进行数值模拟。沿轴颈圆周方向，对流体的黏性剪切力求积分，得到摩擦力，其计算式如下：

摩擦因数计算式为

2 模型和边界条件

2.1 模型简化

图1 显示了文中计算的模型简化过程。在最终构建完成的简化模型中，压力进出口模拟轴承在沟槽部位的入水和出水，静止壁面模拟轴承内衬部分，采用滑移壁面来模拟轴的转动。构建局部沟槽有限元分析模型的目的是能更好地显示沟槽内部流体的流动状态，分析其内部流动和润滑演变过程。

椭圆形沟槽是船舶水润滑轴承结构中最为常见的类型，其结构简单易加工成型，且过渡均匀，可以改善沟槽的结构应力，因此文中选择椭圆形沟槽作为研究对象。简化后的分析模型结构参数如图2 所示，其中l为所取模型的长度，c为轴承间隙，它是轴承表面与轴颈表面之间的距离；a、d分别为沟槽的宽度和深度。基于上述的模型简化假设，为探讨椭圆形沟槽的几何参数对沟槽内部流动特征的影响，文中提出了采用如下参数来表征水润滑轴承的沟槽结构：

式中：h1为深深比，指轴承间隙与沟槽的深度的比值；h2为宽深比，指沟槽宽度与沟槽深度的比值。

2.2 网格划分及尺寸无关性验证

采用有限元法进行分析计算时，网格单元质量和数量越高，其求解计算的精度也越高，但却增加了求解计算的时间。为了减小网格数量和提高求解精度，文中分析计算的网格采用了高阶单元和双精度仿真。

图1 展示了简化后模型的部分网格局部放大图。其中所有单元均为结构化网格，网格单元中无T 形边和自由边，在影响网格质量的因素中主要为单元质量和纵横比，所对应的最优网格质量数值均为1。在文中对应的数值分别为0.964、1.09，说明该网格为高质量的网格，这对计算结果的精度是有益的。

如图3 所示，经对不同数量及不同尺寸的网格进行分析，当流体域网格数量达到39 360，网格尺寸为0.005 mm 时沟槽内部最大压力保持稳定，满足计算要求。

图3 网格尺寸无关性验证Fig.3 Mesh－independent size verification

2.3 CFD 前处理

求解过程中假设流体是理想流体，并考虑了液体空化问题；求解使用简化的多相流模型，即Mixture模型，第一相是水相，第二相是水蒸汽相；空化模型为Zwart－Gerber－Belamri 模型，气相与液相间无相对滑移速度，忽略黏度与表面张力，空化压力为2 340 Pa（绝对压力），蒸发系数50，冷凝系数0.01，气泡直径0.001 mm，成核部位体积分数0.000 5。文中数值求解基于压力求解器，假定润滑状态为水浴润滑状态。

求解方法选用了基于压力－速度耦合的SIMPLEC算法，动量方程采用二阶迎风离散格式进行离散，体积分数方程采用QUICK 离散格式。添加y方向上的力监测，当残差达到所允许的残差或y方向上的升力达到稳定状态时，可认为计算达到收敛状态。

船舶艉轴表面的线速度主要为0～12.56 m／s，所以在进行分析时将滑移壁面线速度数值确定在该范围内。

2.4 湍流模型的选择

通过计算得到轴承的雷诺数与临界雷诺数，得出轴承在运转过程中流体的流动状态为湍流旋流状态。为了更加精确地求解微沟槽内部的流体运动情况，往往需要考虑涡旋黏度的各向异性［20］。Reynolds Stress Model（RSM）算法可以综合考虑强迫涡和自由涡所形成的组合涡态，更能模拟出真实的涡旋及流场，因此选用雷诺应力湍流计算模型。

2.5 模型尺寸无关性验证

为了验证模型尺寸的改变对分析结果趋势的影响，例如流体迹线和压力分布等，是否具有相似性，文中采用相同的边界条件，通过改变整体模型的大小，对宽深比为3，深深比为0.03，深度分别为0.5、1、2、4 和8 mm 的沟槽模型进行分析。图4 选取了深度为4 和8 mm 的结果进行展示，对于其他深度的沟槽结构具有相似的压力和迹线分布。因此，在考虑实际的沟槽尺寸范围内，改变模型的大小，其结果具有相似性。

3 结果与讨论

3.1 速度的影响

图5 分别显示了在不同的滑移速度（轴表面线速度）下沟槽内部的流体流动状态，此时轴承的深深比h1为0.03，宽深比h2为3。依据水流迹线可以得知沟槽内部润滑介质的流动特征。轴的旋转带动轴承间隙内的流体向前流动，当流体到达沟槽部分时，高速入流近似为射流状态。水流速度在近轴面为轴速，高速前进的水流在沟槽内部由于无壁面约束，会通过其边界上活跃的湍流混合将沟槽内的流体卷吸进来而不断扩大，并流向沟槽右端，此为进入沟槽内部水流的自由湍流作用。

图5 不同速度下沟槽内部水流迹线Fig.5 Flow traces inside the trench at different velocities：（a）1 m／s；（b）1.5 m／s；（c）2 m／s；（d）3 m／s；（e）4 m／s

由于入流的自由湍流作用和平行剪切流间的不稳定性，水流截面积不断增大，使得水流在沟槽内部冲击沟槽内壁而折返，受到冲击的沟槽内壁面形成高压区。水流在沟槽底部沿着与转速相反的方向流动，形成低速回流，并出现了第一个强迫涡旋1。在该涡内，涡核部分水流流速最低，沿涡核向外直到沟槽内壁水流速度逐渐增加。流体流动的曲率半径小于沟槽内壁面的曲率半径，小弯的存在使沟槽底部的水流不参与低速回流中，而是受低速回流的影响形成了漩涡3。

水流反向流动的过程中，依据伯努利定律，沟槽中的水流不断汇入轴表面的高速水流中，形成循环，在此期间沟槽内部形成了多个涡旋且会促进沟槽上部的射流。涡旋2 和涡旋3 随着速度的升高而不断加强，涡旋2 最终稳定在沟槽中上位置，涡3 在生长的过程中不断挤压涡1 和涡2 使得涡1 逐渐减小，在此期间在涡2 附近形成了流体动压效应，产生了承载力。

依据上述的沟槽内部流体流动变化过程，整理得到水润滑轴承深沟槽润滑机制示意图如图6 所示，其中靠近出口的沟槽内壁面高压区是由于自由湍流的冲击作用形成的，而非流体动压效应。

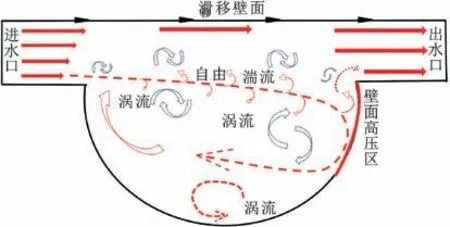
图6 水润滑轴承深沟槽润滑机制Fig.6 Water－lubricated bearing groove lubrication mechanism

低转速下，沟槽内部的介质水流动所形成的涡流较少，水流迹线没有太大的弯曲。涡1 的回流使得在沟槽底部和靠近轴的地方再次生长出小的涡旋。流体速度越大，沟槽底部的涡旋3 的挤压作用越强。不同宽深比下摩擦因数随转速的变化如图7 所示，可以得出不同宽深比下摩擦因数均与转速呈正相关。

图7 不同宽深比下摩擦因数随转速的变化Fig.7 Variation of friction coefficient with rotational speed at different width－to－depth ratio

3.2 深深比的影响

图8 显示了在相对滑移速度为2 m／s，沟槽的宽深比为2 时，随着沟槽深深比的改变，沟槽内部的水流迹线。当深深比很小时，强迫涡旋1 的低速回流很容易汇入从轴承间隙出现的射流中。涡旋2 近似为点涡，是一种理想的自由涡。

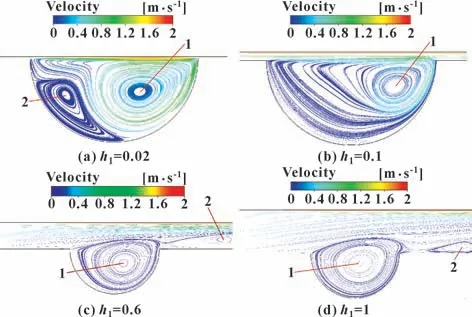
图8 不同沟槽深深比下沟槽内部水流迹线Fig.8 Flow traces inside the trench for different trench depth ratios：（a） h1＝0.02；（b） h1＝0.1；（c） h1＝0.6；（d） h1＝1

随着沟槽深深比的增大，轴的旋转对轴承间隙内水流的文氏效应减弱，更少的水流碰撞到沟槽出口端的内壁上。在沟槽底部水流反向流动的过程中，不会生长出额外的涡旋，此时涡旋1 变为自由涡旋。沟槽深深比越大，来自轴承间隙的水流冲击沟槽内壁越少，直至深深比超过某一数值（见图8（c））；沟槽内水流受间隙内水流的影响，涡旋2 脱落，涡旋1 逐渐生长和扩大，直至该涡旋的尺寸大于沟槽的尺寸。自由涡旋1 会随着深深比的增大而不断生长（见图8（c）（d）），且其循环区域的中心会先向沟槽出水口再向中心移动。

由图8 所示的水流迹线图可知，随着沟槽深深比的增大，即沟槽结构的减小，涡旋1 会逐渐生长，直至漩涡尺寸大于沟槽的尺寸，进而使得轴承间隙内的流体在流经沟槽区域时由较大的流通面积变为较小的流通面积，在名义上形成了一个小的楔形区域，进而满足了流体动压润滑的条件，在沟槽上部形成了局部的高压区，提高了轴承的润滑性能。其润滑机制如图9 所示。

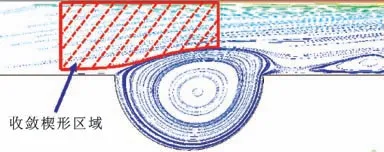
图9 微沟槽提高水润滑轴承润滑性能机制Fig.9 Mechanism of micro－grooves improving the lubrication performance of water－lubricated bearing

图10 显示了沟槽深深比对沟槽内部水流压力的影响，图中压力均为表压。可知：深深比较小时，高压区域出现在沟槽出水端边缘位置（见图10（a）（b）），在涡流的中心区域为低压区域；随着沟槽深深比的增大，沟槽内部流体压力逐渐升高，直至形成流体动压润滑，整个沟槽内部压差变小且均为正压（见图10（c）（d））。

图10 不同沟槽深深比下沟槽内部压力分布Fig.10 Pressure distribution inside the trench for different trench depth ratios：（a） h1＝0.02；（b） h1＝0.1；（c） h1＝0.6；（d） h1＝1

由图10 可得，当沟槽深深比为0.6 时，沟槽内的水压达到最大值；随着深深比再度增大，沟槽内水压反而会减小。因为涡旋1 的生长速度会变得越来越慢，故而在该部分所形成的流体动压作用会先增大后减小。因此，沟槽深度与轴承间隙之间存在一个最佳的深深比。

图11 显示了不同沟槽深深比下沟槽内部的涡流黏度。可知随着深深比的增加，涡流黏度减小，即沟槽内部湍流强度逐渐减弱。图12 显示了不同转速下摩擦因数随深深比变化的曲线。可见，随着深深比的增加，即沟槽结构的减小，摩擦因数先减小而后增大；深深比为20～50 时摩擦因数增加较缓慢，深深比超过50 后摩擦因数增加变快；在深深比为2～5 时摩擦因数具有最小值。

3.3 宽深比的影响

图13 显示的为滑移壁面相对滑移速度2 m／s 时，随着沟槽宽深比的改变沟槽内部的水流迹线。当宽深比很小时，只存在一个准强迫涡旋1（见图13（a））；由于文氏效应的存在，涡旋1 的回流不断汇入高速水流中（见图13（b）—（d））。当沟槽深度增大时（即宽深比减小），轴表面高速水流对沟槽内流体的文氏效应减弱的同时，流体流动的曲率半径小于沟槽内壁面的曲率半径，形成小弯，使位于槽底的自由涡旋2 和沟槽回流区域负压区的增大（见图13（b）—（d））。

图14 显示了宽深比对沟槽内部水流压力的影响，图中压力均为表压。由于文中分析时所采用的深深比较小，所以高压区域出现在沟槽右上位置，漩涡的中心区域为低压区域。随着宽深比的减小，沟槽内部最低水压数值变化不大，低压区所占的比例范围会扩大。因此，沟槽深度越大，沟槽内部水压越小，轴承的润滑性能越差。

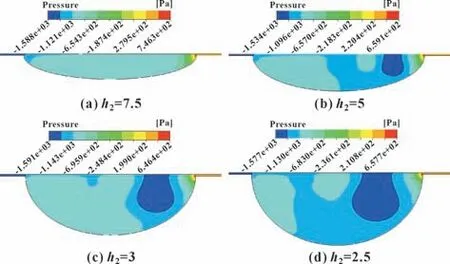
图14 不同宽深比下沟槽内部压力分布Fig.14 Pressure distribution inside the trench for different widthto－depth ratios：（a） h2＝7.5；（b） h2＝5；（c） h2＝3；（d） h2＝2.5

图15 显示了不同沟槽宽深比下沟槽内部的涡流黏度。沟槽内流体黏度随沟槽宽深比的减小而减小，表征了湍流效应的减弱，即流体对流动所表现的阻力越来越小。

图15 不同宽深比下沟槽内部涡流黏度Fig.15 Vortex viscosity inside the trench with different width－todepth ratios：（a） h2＝7.5；（b） h2＝5；（c） h2＝3；（d） h2＝2.5

3.4 水润滑轴承沟槽内部压力分布

通过创建具有沟槽结构的水润滑轴承分析模型，探究沟槽内部的压力分布。所采用的沟槽结构为椭圆形沟槽，轴承和沟槽的具体参数如表1 所示，设定轴承的偏心率为0.5。图16 展示了当转速250 r／min时，水润滑轴承内部水域压力分布云图。

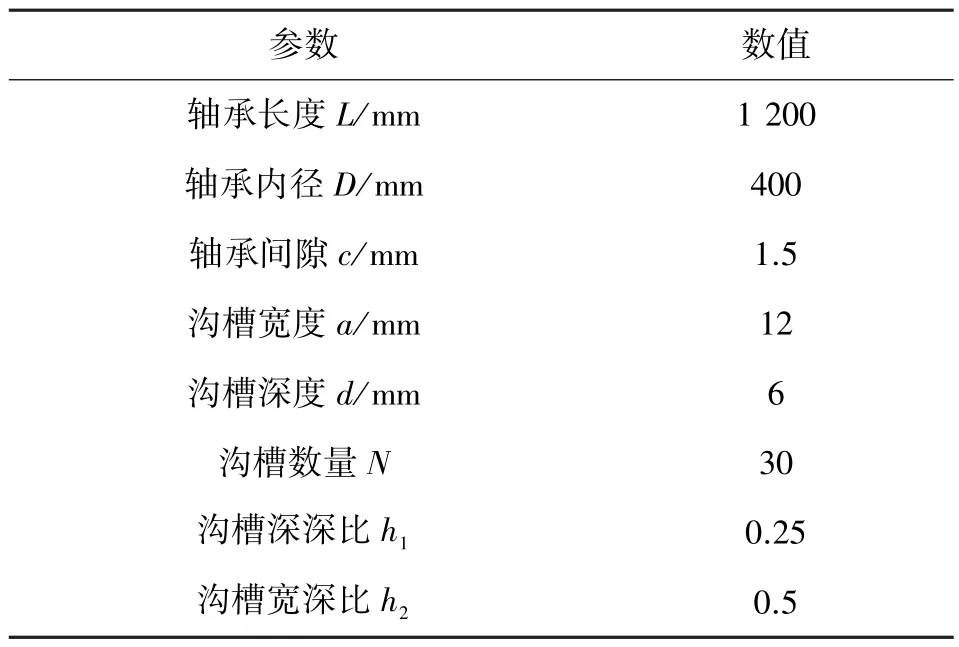
表1 轴承和沟槽结构参数Table 1 Structural parameters of bearings and grooves

图16 轴承内部水域水膜压力分布Fig.16 Water film pressure distribution in the internal waters of the bearing

通过对沟槽内流体流动得出的结论，如图6 所示，沟槽内部高压区会出现在靠近沟槽出口的位置。图17 展示的分别为某高压和某低压区沟槽内壁面的水压分布情况，颜色所代表的压力范围与图17 相同。图17 中轴的转速方向为径向方向向下。经验证沟槽内壁高压区域出现在沟槽出口端，沟槽底部大部分为低压区域，与文中润滑理论相吻合，从而验证了文中润滑理论的准确性。

图17 某高压区沟槽（a）和某低压区沟槽（b）内壁面压力分布Fig.17 Pressure distribution on the inner wall surface of a trench in the high－pressure area（a）and a trench in the low－pressure area（b）

4 结论

建立简化后的船舶水润滑轴承沟槽模型，研究结构参数对水润滑轴承沟槽内部流动特征的影响，揭示沟槽结构对船用水润滑轴承润滑特性的影响机制。主要结论如下：

（1）轴转速越高，沟槽内位于沟槽底部的涡旋会逐渐生长，其挤压沟槽内部其余涡旋和水域的能力越强。

（2）当沟槽结构很小时，沟槽内部的水流形成一个单独的大涡旋，该涡旋的尺寸大于沟槽尺寸。来自轴承间隙的水流在流经沟槽结构时会形成楔形收敛区，形成微动效应，提高了该部分的水膜压力和轴承承载能力。

（3）沟槽宽深比越小，即沟槽深度越大，沟槽内部水流更容易形成多个涡旋，在降低流体黏度的同时也会进一步增加沟槽内的负压区范围，使轴承水膜的压力不连续。