地铁深基坑支护结构参数优化设计研究

杨宗一

（中铁第六勘察设计院集团有限公司，天津 300308）

1 引言

随着城市的发展， 城市中基坑工程的施工技术水平不断提高， 其施工方式也从传统的人工开挖逐步转向机械开挖，基坑的支护结构形式从传统的木桩或桩式支护发展到现在的整体支护结构[1]。根据设计规范要求，在深基坑工程中采用支护方式施工时需对各结构尺寸及受力特点进行合理选择， 以满足工程设计要求。 而在实际施工中，由于不同基坑地质条件差别很大， 因此， 在施工前需要明确各个支护结构参数的最优取值。 基于此，本文对地铁深基坑支护结构参数优化设计研究。

2 构建地铁深基坑支护结构模型

针对整个地铁深基坑施工过程， 按照开挖、 架设支撑结构、施加预加轴力的顺序，循序渐进。 为方便对支护结构参数的优化，采用建模方法对全过程进行仿真，并根据施工阶段的不同情况，分别进行模型参数的求解。 将弹性基础梁按照一定的长度进行节点划分，当出现分界线时，如土层变化面、地下水位面、支撑面、基坑开挖面等，并在土压出现超过0 的位置处增设一个节点[2]。 在支护结构方面，土体的真实应力分布采用均匀荷载，由于采用了节点的受力计算，因此，必须将均匀荷载转化为各节点的集中力和弯矩。 针对模型上每一个节点产生的等效弯矩和预期的变形量进行一对一配列， 并从1~n设置编号。 在未进行开挖时， 对各个节点的静力平衡进行分析，明确模型中各个节点内力与变形协调之间的关系，图1 为节点1 上的内力和节点变形协调关系图。 根据图1 推断出如式（1）所示的平衡关系[3]：

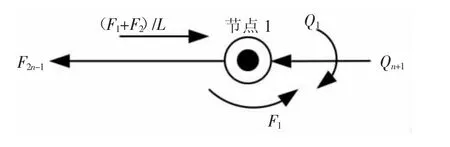
图1 节点1 上的内力和节点变形协调关系图

式中，Q1为节点1 的荷载；Qn+1为节点n+1 的荷载；F1、F2和F2n-1分别为节点1、节点2 和节点2n-1 的变形受力；L 为相邻节点之间的距离。

利用Hooke 定律， 计算深基坑中的支座弹簧和地基上的弹性模量，并将其与支座的弹性模量相结合，得到了相应的弹性系数。

3 不同工况下结构内力与变形求解

在完成对地铁深基坑支护结构模型的构建后， 对不同工况条件下结构的内力与变形进行求解。 将需要求解的参数代入模型当中，由求解问题转化为在各种工作条件下的荷载、结构体系的确定[4]。 根据以上所述的深基坑施工工序，以施工前工作状态下的各因子为基坑的初始状态， 并根据不同工作条件、不同的工作状态，对基坑的初始状态进行了相应的调整。在第一次开挖阶段，荷载体系的变化可为：

式中，{ΔQ}1为第一次开挖工况条件下的节点荷载；ΔQ1、ΔQ2、ΔQ3为各个节点的荷载变化量。 再对结构体系的变化进行分析，将开挖过程中，把土的弹性消解看作是在系数矩阵中相应的元素变成0，表示为：

式中，A 为系数矩阵；j 为常数；n 为开挖面上节点编号。 同样，把基坑开挖时局部土体的弹性消失视为参数矩阵中的对应元素的改变，其表达式为：

式中，S 为局部土体的系数矩阵。 在这一过程中， 若深基坑底部土的弹簧刚度系数发生改变， 则相应的参数矩阵中对应的刚度系数也随之发生变化。 根据上述论述，得到全新的两个系数矩阵。 针对整个施工过程的各个工序，按照上述逻辑，完成对每一工序的数值模拟并得到相应的函数表达结果， 为后续支护结构优化参数的选择提供依据。

4 支护结构优化参数选取

进行优化设计时， 要选取对目标函数的数值有很大的影响，并且在设计中不能很好地掌握的参数，并将其他的参数作为最优参数，通过经验和相关规范的规定来确定，从而使优化过程变得简单[5]。 在地铁深基坑施工中，常见的施工方式包括SMW 工法桩施工、钻孔灌注桩施工等，进一步确定支护结构的优化参数为：锚固深度、支撑支点位置、桩径以及桩间距。 在深基坑工程中，通常采取基桩支护的形式，以满足基坑的安全需要。 当基桩支撑间距扩大时，共同搭建的支护体系的最大弯矩、桩顶间距也会增加，支座所承受的轴向载荷也随之增加，支座的嵌入深度和最大弯矩也逐渐增大。 在工程造价方面，支承的轴力越大，成本也就越高。 所以，在最优设计中，既要考虑最大的弯矩， 又要考虑支撑的轴向（与支护桩长度一致的方向）偏离。

对桩自身而言，桩径对桩身的影响更为显著，随着桩径的增大，混凝土的掺入量也随之增大，而钢筋的配筋率则有所下降；随着桩径的减小，混凝土的用量逐渐减少，而钢筋的比例也相应增加，所以，在设计中选择适当的桩径，既可以满足结构的强度和刚性要求，又可以减少不必要的经济损失。 根据实际情况，桩距的差异主要体现在桩间土拱效应，如果桩间距太小，则无法产生土拱效应，使土体的自稳性无法得到充分的发挥，从而导致桩的数量增多以及经济费用的提高；如果桩间距太大，土压力会使土体拱效应发生破坏，引起桩间土不稳定，严重影响基坑的安全。 因此，正确地选择桩距是非常有必要的。

5 支护结构优化约束条件处理与优化适应度确定

在完成对支护结构优化参数的选取后， 确定支护结构的优化目标函数，在实际工程中，设计人员常常要同时考虑多个期望，如成本低、工期短、对环境影响较小等。 因此，将支护结构优化目标设计为式（5）所示：

式中，y 为支护结构优化目标函数；minf（X）为最低成本、最短工期和对环境的最小影响。 在深基坑支护结构参数优化设计中，由于目标函数的极限值存在一定的局限性，因此，可以将其划分为：设计变量自身的约束；设计变数间的连贯性限制；需要符合相关的设计规范， 包括多支点支护结构的嵌固深度检验、基坑整体稳定性检验、抗隆起稳定性检验、管涌稳定性校核及抗倾覆校核。

将式（1）~ 式（4）的约束条件定义为gi（x），表达式为：

采用构造惩罚函数的方法来处理此约束， 惩罚函数表达式为：

式中，F（x，σ）为惩罚函数；σ 为惩罚因子。

当gi（x）的取值＞0 时，把以上的限制问题转化成一个没有限制的问题。 选取单位宽度的桩材造价作为目标函数，确定支护结构参数优化后的适应度。 适应度又称适应值，指某已知承载力的支护结构在不同工况条件（地质、结构内力和变形情况）下保持安全度的相对能力，优化后的支护结构适应度值越大，则其承受能力越大，安全系数越高，其公式为：

式中，F（X）为适应度；h 为深基坑的开挖深度；H 为桩长；d 为桩的嵌固深度；D 为桩径；s 为桩间距。 根据本文上述优化思路，对深基坑支护结构参数进行优化，并根据公式（8）计算结果中选择适应度最高数值进行参数优化。

6 实例应用分析

以某地铁1 号线某车站为例， 该车站为地下2 层岛式站台车站，基坑开挖深度为18.5 m，通过钻探勘察揭示基坑土层地质情况，如表1 所示。

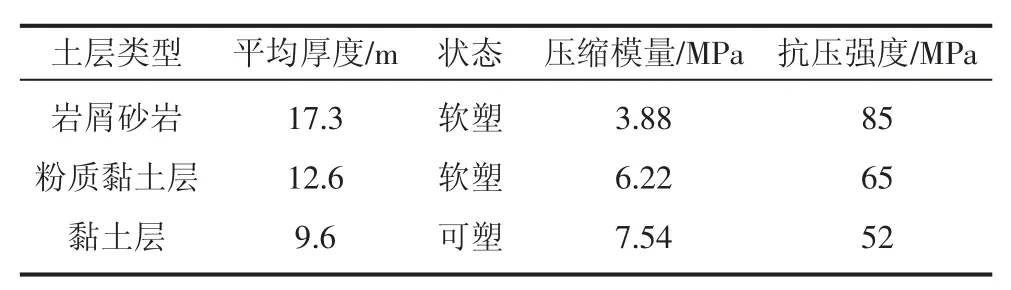
表1 基坑土层地质情况

如表1 所示，基坑土体存在质地比较坚硬的岩屑砂岩。 黏土层土体含水量较大， 达到20%。 经对该项目水文资料的调研， 得出了该项目地下水位于基坑底部， 主要来源为天然降水，地下水沿南北方向移动，其下游水位在41.6~41.8 m 较为平稳。 该工程项目基坑开挖支护结构采用灌注桩支撑体系。 优化前灌注桩的长度为31.6 m，桩径为1 m，桩间距为1.8 m。 该工程支护结构图如图2 所示。

图2 支护结构图

支护结构优化后的参数为：灌注桩的长度约28.5 m，桩径为0.9 m，桩间距为1.5 m。

利用公式（8）计算得出，应用本文上述优化设计思路前的结构参数适应度和应用后的结构参数适应度， 针对每个施工工序分别记录，得到如表2 所示结果。

表2 优化前后支护结构参数适应度及成本记录表

从表2 中的结果可以看出， 优化前支护结构的适应度仅在1.2~1.3 范围内波动，而优化后支护结构的适应度均超过2，优化后的支护结构参数的适应度F（X）值更高，支护结构的承受能力得到了提高，进而表明其安全系数也得到了提高。 从成本数据可知，本文方法对经济性也进行了有效优化，成本明显降低，因此，说明上述设计思路可实现对结构参数的优化，具有极高的可行性。

7 结语

通过本文对地铁深基坑支护结构的参数进行优化， 采取理论分析与实例应用验证相结合的方法，取得了良好的效果。方案优化后， 支护结构能够充分满足地铁深基坑设计规范要求。 同时优化后支护结构具有良好的适应度，提高了支护结构的安全性，减少了施工成本。