侧压型竹层板用竹条分级研究

谢力生,陶钧,廖彬彬,刘嘉诚,朱芳钰

(中南林业科技大学材料科学与工程学院,长沙 410004)

竹子生长速度快、强度高、资源丰富,以竹代木生产需求日益增长的结构用集成材具有重要意义。从竹筒加工获得的竹条具有各向异性、带竹节、径向材质差异大等特点[1-3],直接用竹条组坯制造集成材,产品难以达到结构用材要求,竹条需要进行分级使用[4-5]。研究表明,竹条的密度与其径向弹性模量和抗弯强度均呈现出较好的线性关系[6],但密度分级只能在一定程度上优化竹条的力学性能[7];而竹条的径向弹性模量与其抗弯静曲强度呈显著的线性关系[8-10]。竹条弦向和径向(含青面朝上和朝下)任意2个弹性模量之间都存在较强的线性相关性[11],由一个方向的弹性模量可以推测出另外2个方向上的弹性模量。由此可知,采用弹性模量对竹条分级具有科学合理性。但前述竹条分级研究成果均是依据测试竹条某一节间的抗弯静曲强度和弹性模量而获得的,没有考虑竹节和测试部位的影响。

用竹条制造竹集成材,其层板有平压型(竹条平置窄面胶合)和侧压型(竹条侧立宽面胶合)2种;侧压型竹层板的抗弯力学性能优于平压型,结构用竹集成材一般采用侧压型竹层板[12-13]。组成侧压型竹层板的竹条在层板受弯时承受弦向荷载,故最好依据其弦向抗弯静曲强度来进行分级。对于侧立的竹条,其宽度(约为5.5 mm)只有其高度的1/4左右,且多有侧向弯曲或扭曲,很容易倾倒,不易测试其抗弯弹性模量和静曲强度。若能找出竹条径向抗弯弹性模量与其弦向抗弯弹性模量和静曲强度之间的关系,并建立其数学模型,则理论上可以通过测试竹条的径向抗弯弹性模量来预测其弦向静曲强度,实现其分级,从而解决测试难的问题。经过精刨而成的规格竹条,人眼或机器不容易准确地判别其近青面和近黄面,而竹条径向两面的抗弯弹性模量是不同的。若将径向两面的抗弯弹性模量平均值作为竹条径向抗弯弹性模量值,则不必判别近青面或近黄面,为竹条径向抗弯弹性模量的测试提供了方便。整根竹条的不同部位其径向抗弯弹性模量一般都是不同的,如何快速获得代表整根竹条的径向抗弯弹性模量一直困扰着相关研究者。若竹节的影响可忽略不计,竹条长度方向中心位置的径向抗弯弹性模量可以作为整根竹条的代表值,则竹条可以实现在线快速测试、分级。为此,笔者就相关内容开展了研究,期望能为侧压型竹层板用竹条实现可靠、实用的在线快速分级提供理论依据。

1 材料与方法

1.1 试验材料

精刨碳化竹条,由湖南省益阳市某竹材公司提供,由4～6年生毛竹为原材料制作而成,含水率约为10%,尺寸为21.5 mm(宽)×5.6 mm(厚)×1 200 mm(长)。

单组分聚氨酯胶黏剂,由广东清远容能化工有限公司生产,型号为ZA-302,固含量≥60%,黏度500～1 500 mPa·s。

1.2 仪器设备

木工精密圆锯机、木工小型带锯机、数显游标卡尺、G字形木工夹等。万能力学试验机,由济南试金试验设备有限公司生产,型号为MWD-50。木工平刨床,由佛山亿迈通设备有限公司生产,型号为MB504。

1.3 试验方法

任取竹条15根,按照GB/T 17657—2022《人造板及饰面人造板理化性能试验方法》中的三点弯曲法测试竹条中部节间中点位置的径向抗弯性能,观察荷载-位移曲线,发现荷载小于250 N时,竹条均处于弹性变形阶段。由此确定,测定竹条径向弹性模量时,加载荷载至250 N,取下限荷载140 N和上限荷载240 N时的位移值计算抗弯弹性模量。再任取竹条15根,将竹条从宽度方向一分为二(便于竹条侧立),按前述方法测试竹条中部节间中点位置的弦向抗弯性能,观察载荷-位移曲线,发现荷载小于100 N时,竹条均处于弹性变形阶段。由此确定,测定竹条弦向弹性模量时,加载荷载至100 N,取下限荷载30 N和上限荷载80 N时的位移值,计算抗弯弹性模量。

任取竹条30根,先按前述方法测试各竹条距端部大于220 mm(为了满足试件的跨度要求)的各节间中点位置(共计102个)的径向两面(近竹青面和近竹黄面分别在拉伸侧)抗弯弹性模量;然后将各竹条从宽度方向一分为二,分别取其中一根按相同方法测试竹条各对应节间中点位置(102个)的弦向抗弯弹性模量;再分别取其中另一根按照GB/T 17657—2022中的方法测试竹条中部1个节间中点位置(共计30个)的弦向静曲强度。测试所得各抗弯弹性模量和弦向静曲强度分别记入相应的数据表中,处理、分析测试数据,探讨竹条节间中点位置径向两面抗弯弹性模量之间、径向两面抗弯弹性模量平均值与弦向抗弯弹性模量之间、弦向静曲强度与弦向抗弯弹性模量之间,以及弦向静曲强度与径向两面抗弯弹性模量平均值之间的关系,分别建立回归模型。

任取竹条90根,先按前述方法测试各竹条距端部大于220 mm的各节部中点位置(共计245个)和节间中点位置(共计248个)的径向(近竹青面在拉伸侧)抗弯弹性模量;然后将各竹条从宽度方向一分为二,分别取其中一根先按前述方法测试竹条各对应节部中点位置(245个)和节间中点位置(248个)的弦向抗弯弹性模量,接着按前述方法测试竹条中部节间中点位置(共计90个)的弦向静曲强度;取其中另一根按相同方法测试竹条中部节部中点位置(共计90个)的弦向静曲强度;测试所得各抗弯弹性模量和弦向静曲强度分别记入相应的数据表中;处理、分析测试数据,探讨竹条中部节间(或节部)中间点弦向抗弯弹性模量与竹条多点(整根竹条上的所有节间和节部位置测试点)弦向抗弯弹性模量平均值、竹条中间点径向抗弯弹性模量与竹条多点径向抗弯弹性模量平均值和多点弦向抗弯弹性模量平均值之间的关系,分别建立其数学模型。

根据前述90根竹条所测得的竹条中间点的径向抗弯弹性模量和弦向静曲强度,以0.5 GPa为间距对弹性模量在8.0～11.0 GPa范围的竹条进行分级,可分为E80、E85、E90、E95、E100、E105和E110 7个等级;根据各等级竹条所对应的弦向静曲强度,绘制不同等级竹条的弦向静曲强度箱形图;探讨通过测试竹条径向中间点抗弯弹性模量对竹条分级的有效性。

任取竹条128根,按照前述方法对竹条中部位置进行径向两面抗弯弹性模量测试,记录试验数据并计算两面抗弯弹性模量的平均值;参照前述竹条分级方法,依据两面抗弯弹性模量的平均值对竹条进行分级;从分级竹条中挑选出E85至E110共6个等级竹条各10根(共60根),另外随机抽取20根不分级的竹条;在竹条的近青面手工涂刷单组分聚氨酯胶黏剂(施胶量为180 g/m2),相邻竹条均以近青面与近黄面贴合层叠组坯,用G字形木工夹侧向夹紧,24 h后缷下夹具,最终制得6块不同等级的侧压型竹层板和2块对照组竹层板(宽56 mm、厚21.5 mm、长1 200 mm);放置48 h后,按照GB/T 17657—2022中的方法测试各竹层板的抗弯弹性模量和静曲强度;分析竹层板的抗弯弹性模量和静曲强度与竹条等级之间的内在联系,验证采用竹条中间部位的径向抗弯弹性模量对侧压型竹层板竹条进行分级的有效性和可靠性。

2 结果与分析

2.1 竹条节间中心各方向弹性模量之间的关系

根据30根竹条102个节间中心位置各向抗弯弹性模量的测试数据,可以得到径向两面(近青面和近黄面)抗弯弹性模量之间的数据散点图(图1),以及径向两面抗弯弹性模量平均值与弦向抗弯弹性模量之间的数据散点图(图2)。

图1 径向近黄面与近青面抗弯弹性模量的关系Fig. 1 The relationship between radial MOE near the bamboo yellow and radial MOE near the bamboo green

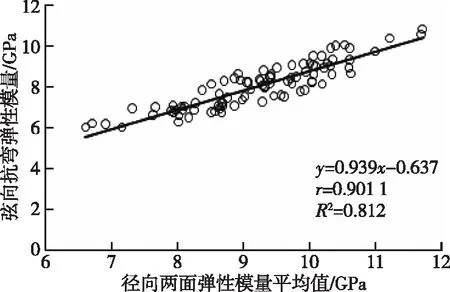
图2 弦向MOE与径向两面MOE平均值的关系 Fig. 2 The relationship between tangential MOE and the average about both side of radial MOE

从图1可以看出,竹条节间中心径向两面的抗弯弹性模量之间存在极显著的线性关系(r=0.951 8),径向近青面抗弯弹性模量随着近黄面抗弯弹性模量的增加而增大。近黄面抗弯弹性模量Eh与近青面抗弯弹性模量Eq的数学关系模型为Eh=1.049Eq-0.759(R2=0.906)。从图2可以看出,径向节间中心两面抗弯弹性模量的平均值与弦向抗弯弹性模量之间存在较显著的线性关系(r=0.901 1),竹条弦向抗弯弹性模量随径向两面抗弯弹性模量平均值的增加而增大。弦向抗弯弹性模量Ex与径向两面抗弯弹性模量平均值Ep的数学关系模型为Ex=0.939Ep-0.637(R2=0.812)。可见,竹条同一节间中心位置各方向的抗弯弹性模量之间均存在显著的线性关系,测试其中一个方向的抗弯弹性模量即可推测出其他方向的抗弯弹性模量;通过测试竹条节间中心径向两面的抗弯弹性模量并计算其平均值,可以很好地预测出对应节间中心的弦向抗弯弹性模量。宋光喃[11]研究发现,竹条任意2个弹性模量之间都存在较强的线性相关性,与本研究的结论一致。

2.2 竹条节间中心位置不同方向的弹性模量与弦向静曲强度之间的关系

根据30根竹条的中部节间中心位置的弦向抗弯弹性模量、静曲强度和径向两面抗弯弹性模量平均值,可以得到弦向抗弯弹性模量与其静曲强度的关系数据散点图(图3)和径向两面抗弯弹性模量平均值与弦向静曲强度关系的数据散点图(图4)。

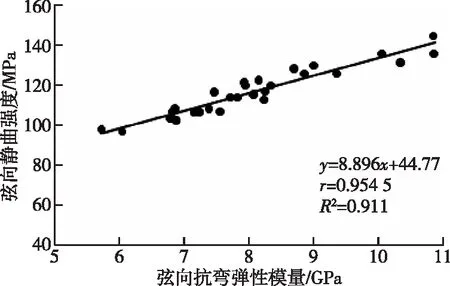
图3 弦向静曲强度与弦向抗弯弹性模量的关系Fig. 3 The relationship between tangential MOR and tangential MOE

图4 弦向静曲强度与径向两面抗弯弹性模量的关系Fig. 4 The relationship between tangential MOR and radial bending MOE on both sides

30根竹条中部节间中心位置的弦向静曲强度为97～145 MPa,弦向抗弯弹性模量为5.72～10.87 GPa,径向两面抗弯弹性模量的平均值为7.15～11.73 GPa,均相差很大,这充分说明竹条分级使用的必要性。只有分级使用,才能做到有效使用和安全使用。

由图3可以看出,竹条中部节间中心位置的弦向静曲强度与其抗弯弹性模量之间存在极显著的线性关系(r=0.954 5),竹条弦向静曲强度随着其抗弯弹性模量的增大而增大,这也与宋光喃[11]的研究结论一致。弦向静曲强度Rx与其抗弯弹性模量Ex之间的数学关系模型为Rx=8.896Ex+44.77(R2=0.911)。可见,通过测量竹条弦向抗弯弹性模量可以很准确地推测其静曲强度。由图4可以看出,竹条中部节间中心位置的弦向静曲强度与其径向两面抗弯弹性模量平均值之间存在较显著的线性关系(r=0.908 3),竹条弦向静曲强度随着径向两面抗弯弹性模量平均值的增大而增大。弦向静曲强度Rx与径向两面抗弯弹性模量平均值Ep之间的数学关系为Rx=10.61Ep+18.26(R2=0.825)。可见,通过测量竹条径向两面抗弯弹性模量并计算其平均值,可以很好地推测其弦向静曲强度;或者说明通过对竹条径向两面抗弯弹性模量平均值进行分等,可以很好地实现对竹条弦向静曲强度的分级。

2.3 竹节对竹条弹性模量的影响

对90根竹条的248和245个节部测试位置所测得的弦向抗弯弹性模量和径向(近青面受拉)抗弯弹性模量数据进行统计(表1)和分析,可以得到多点弦向抗弯弹性模量平均值(整根竹条上所有测试位置的抗弯弹性模量平均值)与中间点抗弯弹性模量关系(图5)、多点径向抗弯弹性模量平均值与中间点抗弯弹性模量关系(图6),以及多点弦向抗弯弹性模量平均值与中间点径向抗弯弹性模量关系(图7)的数据散点图。

表1 竹条各点抗弯弹性模量Table 1 MOE of bamboo strips at each point

图5 多点弦向MOE平均值与中间点弦向MOE的关系Fig. 5 The relationship of all test points tangential MOE and the middle test point tangential MOE

图6 多点径向MOE平均值与中间点径向MOE的关系Fig. 6 The relationship of all test points radial MOE and the middle test point radial MOE

图7 多点弦向MOE平均值与中间点径向MOE的关系Fig. 7 The relationship of all test points tangential MOE and the middle test point radial MOE

从表1可以看出,对于全体试件,竹条中部的抗弯弹性模量(无论是节间还是节部或是节部和节间中点的平均值,也不论是弦向还是径向)与多点抗弯弹性模量的平均值,其大小范围、平均值、标准差和变异系数都相差甚微。这说明总体而言,竹节对竹条抗弯弹性模量的影响很小,竹条中部的抗弯弹性模量可以代表整根竹条的抗弯弹性模量。有研究表明,带节竹材的抗弯强度与节间相比有一定程度降低的趋向,但差异不显著[14];竹条节部的弯曲强度较节间大约3.14%[15]。总之,节部与节间的弯曲强度差异很小,与本研究的结果具有一致性。

从图5可以看出,竹条多点弦向抗弯弹性模量平均值与竹条节间或节部中间点弦向抗弯弹性模量之间存在较显著的线性关系(r=0.917 1)。竹条多点弦向抗弯弹性模量平均值Exd随着竹条节间或节部中间点弦向抗弯弹性模量Exz的增大而增大,一元线性经验回归方程为Exd=0.816Exz+1.771(R2=0.841)。这说明仅测量竹条中间点(无论是节间还是节部)的弦向抗弯弹性模量就能较好地推测出整根竹条的弦向抗弯弹性模量(多点的平均值)。

从图6可以看出,竹条多点径向(近青面受拉)抗弯弹性模量平均值与竹条节间或节部中间点径向抗弯弹性模量之间存在显著的线性关系(r=0.934 3)。竹条多点径向抗弯弹性模量平均值Ejd随着竹条节间或节部中间点径向抗弯弹性模量Ejz的增大而增大,一元线性经验回归方程为Ejd=0.867Ejz+1.267(R2=0.873)。这说明仅测量竹条中间点(无论是节间还是节部)的径向抗弯弹性模量就能较好地推测出整根竹条的径向抗弯弹性模量(多点的平均值)。

从图7可以看出,竹条多点弦向抗弯弹性模量平均值与竹条节间或节部中间点径向(近青面受拉)抗弯弹性模量之间存在较好的线性关系(r=0.822 8)。竹条多点弦向抗弯弹性模量平均值随着竹条节间或节部中间点径向抗弯弹性模量增大而增大,一元线性经验回归方程为Exd=0.659Ejz+ 3.419(R2=0.677)。这说明仅测量竹条中间点(无论是节间还是节部)的径向抗弯弹性模量就能较好地推测出整根竹条的弦向抗弯弹性模量(多点的平均值)。

2.4 中间点径向抗弯弹性模量对竹条分级的有效性

90根竹条所测得的竹条中间点径向抗弯弹性模量为6.1～12.1 GPa,以0.5 GPa为间距对弹性模量在8.0～11.0 GPa范围的竹条进行分级,各等级(E80～E110)竹条所对应的试件量和弦向静曲强度统计如表2所示,不同等级竹条的弦向静曲强度箱形图如图8所示。

表2 不同等级竹条的弦向静曲强度Table 2 Tangential MOR of bamboo strips of different grades

图8 不同等级竹条的弦向静曲强度Fig. 8 Tangential MOR of bamboo strips of different grades

由表2可知,E80～E110七等级竹条共计80根,占总数的88.89%。其中,E90～E105 4个等级的竹条共计61根,占总数的67.78%。

由表2和图8可知,随着竹条径向抗弯弹性模量等级的增大,各等级竹条弦向静曲强度的平均值呈近似直线增大。从E80到E110,竹条的弦向静曲强度平均值从124.76 MPa增大到156.00 MPa,增长了25.04%;竹条每提高一个等级,其弦向静曲强度平均增加4.17%。这说明具有很好的分级效果,即通过竹条中间点径向抗弯弹性模量分等可以对竹条的弦向静曲强度进行有效分级。

2.5 侧压型竹层板用竹条分级效果验证

制造不同等级侧压型竹层板的竹条,其径向抗弯弹性模量统计如表3所示。由表3可知,未经分级的竹条变异系数达11.29%,而经过分级之后,不同等级的竹条变异系数均稳定在2%以内,降低了82%以上。由此可知,通过分级可以显著降低竹层板组成单元——竹条之间径向抗弯弹性模量的差异。

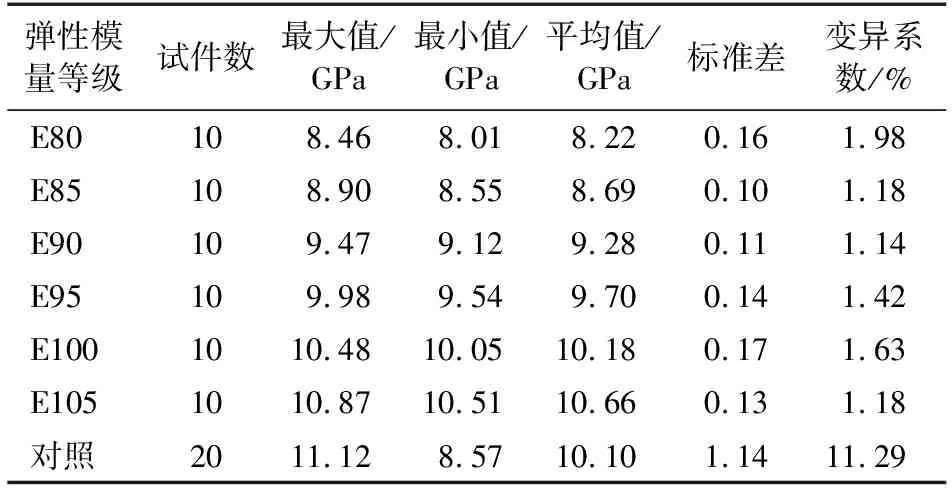
表3 不同等级竹条的径向抗弯弹性模量Table 3 Radial MOE of bamboo strips of different grades

由各等级竹条制备的竹层板抗弯弹性模量和静曲强度如图9所示。由图9可知:竹层板的抗弯弹性模量和静曲强度与竹条等级均呈现正相关性;随着竹条等级的提高,竹层板的抗弯弹性模量和静曲强度成比例地增大。由此可知,对于侧压型竹层板用竹条,采用中间点径向抗弯弹性模量进行分级效果显著。

图9 不同等级竹层板的抗弯弹性模量和静曲强度Fig. 9 MOE and MOR of different bamboo laminates grade

3 结 论

通过研究竹条节间中心各方向弹性模量之间及其与弦向静曲强度之间的关系,以及竹节对竹条弹性模量的影响,并对竹条采用中间点径向抗弯弹性模量分级的有效性和对侧压型竹层板的抗弯性能进行验证,得到以下结论:

1)通过测量竹条节间径向两面抗弯弹性模量,可以较准确地推测其弦向抗弯弹性模量;

2)通过测试竹条某节间径向两面抗弯弹性模量,可以很好地预测该位置的弦向静曲强度;

3)仅测量竹条中间点(无论是节间还是节部)的径向抗弯弹性模量,就能较好地推测出代表整根竹条的弦向抗弯弹性模量;

4)采用竹条中间点径向抗弯弹性模量分等,可以实现对竹条(弦向静曲强度)的有效分级;

5)按竹条中间部位的径向抗弯弹性模量对竹条进行分级,其侧压型竹层板的分级效果显著。