求椭圆离心率常用的三种方法
王建辉

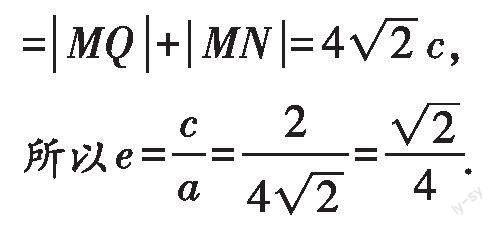

椭圆的离心率是椭圆的一个重要性质,它是反映椭圆的扁平程度的量.求椭圆的离心率问题比较常见.这类问题常与平面几何、三角函数、平面向量等知识相结合,侧重于考查同学们的逻辑推理和数学运算能力.那么,求椭圆的离心率有哪些方法呢?下面结合实例进行探讨.
一、公式法
解:因为椭圆的长轴长是短轴长的2倍,
本题较为简单,由题意可以很容易确定椭圆中参数a、b之间的关系,直接根据椭圆方程中参数a、b、c之间的关系[a2=b2+c2],即可求得[c]与[a]的比值,从而求得椭圆的离心率.
解:因为椭圆的右焦点为[F2,0],所以c=2,
因为P为椭圆的左顶点,
所以[PF=a+c=a+2=5],解得[a=3],
我们首先根据题意可以确定c的值;然后根据P点的位置,确定a的值,即可根據椭圆离心率的公式求得问题的答案.
二、几何性质法
几何性质法是指利用平面几何图形的性质解题.在求椭圆的离心率时,我们可以根据题意画出几何图形,将椭圆参数方程中的a视为长半轴长、b视为短半轴长、c视为焦半径,根据椭圆、三角形、平行四边形、梯形的性质来求得椭圆的长半轴长、短半轴长、焦半径,或建立三者之间的关系式.
解:由题意得[MF1=F1F2=2c],
由椭圆的定义得[MF2=2a-2c],
记[∠MF1F2=θ],则[∠AF2F1=∠MF2A=θ],[∠F1F2M=∠F1MF2=∠MAF2=2θ],
则[AF2=AF1=2a-2c],所以[AM=4c-2a],
解答本题,需运用相似三角形的性质建立关于[MF1、F1F2][AM、MF2]的关系式,并根据椭圆的定义,即在平面内到两个定点的距离之和为定值的点的轨迹,确定[MF1、F1F2][AM、MF2]与a、c之间的关系,从而使问题获解.
离心率[e=]______.
解:设内切圆与AM切于Q,与[AF1]切于P,
由圆的对称性知[AF1=AF2],
所以[PF1=QF2],即[NF1=QF2],
所以[2a=MF2+MF1=MQ-QF2+MN+NF1]
我们先结合图形明确点、圆、椭圆之间的位置关系;然后根据椭圆的定义将问题转化为线段问题,即可根据圆的对称性、圆与切线的位置关系建立线段[MF2、MF1]、
[MQ、QF2、MN、NF1]之间的关系,得到关于[a、c]的关系式,进而求出椭圆的离心率.用几何性质法解题的计算量较小,有利于提升解题的效率.
三、构造齐次式
解:设[Mx1,y1],[Qx2,y2],则[N-x1,-y1],[P3x1,0],
设直线[MN]、[QM]、[NP]的斜率分别为[k1]、[k2]、[k3],
解:因为点C、F是线段AB的三等分点,
由图3可知C为[AF]的中点,右焦点为[F2],
所以[AF2//OC],所以[AF2⊥x]轴,
先由点C、F是线段[AB]的三等分点可得[AF2//OC];再根据线段的对称性可求得B点的坐标;最后将其代入椭圆中,即可建立关于a、b、c的二次齐次式,进而得到关于椭圆离心率e的方程.

