如何解答不等式问题
史淑敏

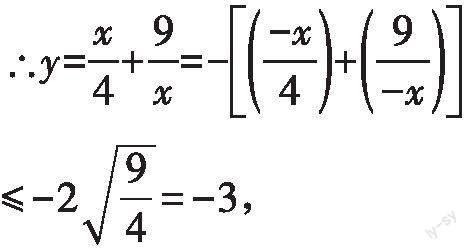
不等式问题有很多种,常见的有线性规划问题、一元二次不等式问题、抽象函数不等式问题、证明不等式问题等.每种不等式问题的特点、命题形式、解法均有所不同.下面结合实例进行探讨.
一、线性规划问题
线性规划问题往往会给出一组二元一次不等式,要求在线性约束条件下求目标函数的最大值或最小值.解答这类问题,要先将不等式所对应的二元一次方程看作一条直线,根据二元一次不等式组画出可行域;然后挖掘目标函数的几何意义,将其看作直线的斜率、截距、距离等;再在可行域内寻找目标函数取得最值时的点、线段,从而求得最值.
解:不等式组表示的可行域如图1中阴影部分所示.
解答线性规划问题,需在平面直角坐标系中,画出不等式所对应的方程所表示的直线;然后确定不等式所表示的平面区域在直线的哪一侧,画出可行域.值得注意的是,若不等式中无等号,则直线应画成虚线;有等号,则直线应画成实线.
将三个方程[x-y+1=0],[x-2y=0],[x+2y-2=0],两
二、一元二次不等式问题
一元二次不等式问题常以选择题、填空题的形式出现.此类问题侧重于考查函数、集合、不等式的性质.解答一元二次不等式问题,需首先根据一元二次不等式ax2+bx+c>(<)0,建立方程ax2+bx+c=0;然后利用求根公式,或通过因式分解求得方程ax2+bx+c=0的根;再画出一元二次函数y=ax2+bx+c的图象,根据△与0的关系,图象上的点与x轴的位置关系,确定不等式的解集.
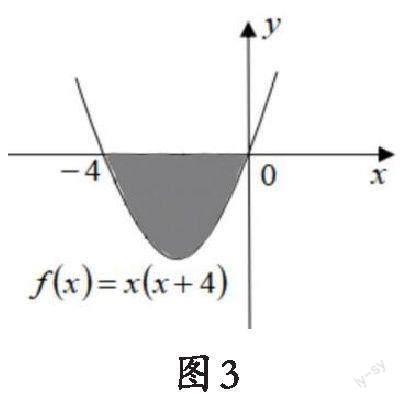
解:画出[y=xx+4]的图象,如图3所示,可知[A=x-4 ∵[x<0], ∴[A?B=-4,-3],∴正确答案为[B]项. 先画出[y=xx+4]的图象,即可确定[x]轴下方的图象上的点的集合,即为A的解集;然后根据基本不等式,求得y的取值范围,即可求得集合B. 例4.若不等式[x2-5x+6<0]的解集满足关于[x]的不等式[2x2-9x+a<0],则[a]的取值范围为_____. 解:解一元二次不等式[x2-5x+6<0]得[2 即不等式的解集为[2,3], 令[fx=2x2-9x+a], ∵不等式[2x2-9x+a<0]的解集滿足[2 解不等式组可得[a≤9],即[a]的取值范围为[-∞,9]. 首先求得一元二次不等式[x2-5x+6<0]的解集;然后根据“不等式[2x2-9x+a<0]的解集满足[2 三、抽象函数不等式问题 抽象函数不等式问题的难度一般较大,由于问题中没有给出具体的解析式,所以往往需重点研究函数的性质,利用函数的对称性、周期性、奇偶性将不等式两侧式子的自变量转化到同一个单调区间内,根据区间上函数的单调性来解不等式. [A.-2,0?2,+∞] [B.-3,-1?0,1] [C.-2,0?2,+∞] [D.-2,0?0,2] 解:∵定义在[R]上的奇函数[fx]在[-∞,0]上单调递减, ∴函数[fx]在[0,+∞]上单调递减, ∵[f2=0],∴[f-2=0], [f0=0], 当[x∈-∞,-2?0,2]时, [fx>0], 当[x∈-2,0?2,+∞]时, [fx<0], ∴正确答案为[D]项. 解答本题,要先根据函数的奇偶性,判断出当[-∞,0]和[0,+∞]时函数的单调性,以及在各个区间上函数值的符号;然后根据函数的单调性,去掉函数在x>0、x<0时的符号“f ”,得到关于[x]的不等式,从而求得不等式的解集. 可见,解答不等式问题需注意:(1)将问题与函数、方程关联起来,将问题进行合理的转化;(2)灵活运用数形结合思想、转化思想来辅助解题;(3)熟练运用解一元一次不等式、一元二次不等式的技巧.

