灵活运用数学思想,提升解答立体几何问题的效率
吴飞鹏

立体几何问题对同学们的抽象思维和空间想象能力有较高的要求.在解答立体几何问题时,灵活运用数学思想,如转化思想、数形结合思想、分类讨论思想等能有效地提升解题的效率.下面结合实例进行探讨.
一、转化思想
转化思想是指采用某些手段,如换元、构造函数、添加辅助线等手段,使问题转化,以从另一个角度寻找到解题的思路.在解答立体几何问题受阻时,可运用转化思想,将问题与向量的运算法则、函数的单调性、方程的根等关联起来,通过添加辅助线,把问题转化为函数、向量、方程等问题来求解.这样就能另辟蹊径,快速获得问题的答案.
例1.如图1所示,四棱锥[A-BCDE]满足棱长[AB=CD=2BE=22],[AC=BC=2],[BE]∥[CD],侧棱[DA]的中点是[F],且[CD⊥]平面[ABC].
(Ⅰ)证明:[EF]∥平面[ABC];
(Ⅱ)证明:平面[ACD⊥]平面[BCDE].
(Ⅲ)求直线[BD]与平面[AED]的夹角[θ]的正弦值.
解:(Ⅰ)设[M]是侧棱[AC]的中点,连接[FM,BM],
因为侧棱[DA]的中点是[F],侧棱[AC]的中点是[M],
所以△[ACD]的中位线是[MF],
从而可知四边形[EFMB]是平行四边形,因此[EF]∥[BM].
所以[AC2+BC2=AB2],因此[AC⊥BC].
而[CD⊥]平面[ABC],[AC?]平面[ABC],则[CD⊥AC].
而[BC?CD=C],则[AC⊥]平面[BCDE].
又[AC?]平面[ACD],故平面[ACD⊥]平面[BCDE].
(Ⅲ)因为[CD⊥]平面[ABC],所以[CD⊥CA],[CD⊥CB].
所以[AC2+BC2=AB2],所以[AC⊥BC].
因此三条直线[CA,CB,CD]两两互相垂直,分别以[CB,CA,CD]为[x,y,z]轴,建立空间直角坐标系[C-xyz],如图2.
我们先根据线面平行的判定定理证明[EF]∥平面[ABC],并根据面面垂直的判定定理证明平面[ACD⊥]平面[BCDE],即可得到三条互相垂直的直线[CA,CB,CD],据此建立空间直角坐标系,求得各个点的坐标,进而运用转化思想,将问题转化为空间向量的坐标运算问题;然后通过空间坐标运算,求得[BD]的方向向量以及平面[AED]的法向量,即可根据向量的数量积公式求得夹角.运用转化思想解答立体几何问题,需寻求问题与其他知识之间的联系,从而将问题转化.
二、分类讨论思想
有些立体几何问题比较复杂,需要分多种情况进行讨论,此时可灵活运用分类讨论思想,将问题中点的位置、直线与平面所成的夹角、图形的形状等视为讨论对象,按照一个统一的标准对其进行分类讨论.在运用分类讨论思想解题时,要细致地划分并讨论每一个类别,不重复、不遗漏任何情况,最后还需注意对各种讨论结果进行汇总.
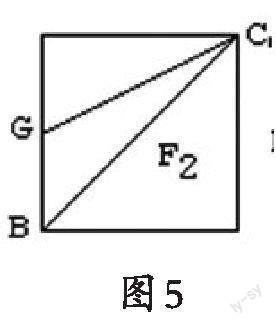
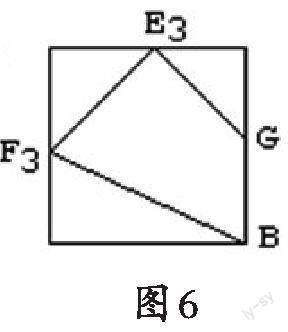
例2.如图3所示,已知正方体[ABCD-A1B1C1D1]的棱长为[1],侧面[AA1D1D]的中心是点[F],棱[C1D1,BB1]的中点分别为[E,G],求空间四边形[BGEF]在该正方体各面上的最大射影面积.
解:分下列三種情况进行讨论、分析.
由于正方体具有对称性,所以只需考虑空间四边形[BGEF]在正方体的三个相邻面上的投影面积,运用分类讨论思想,分别讨论下底面、右侧面、前面上的射影面积,即可获解.
三、数形结合思想
解答立体几何问题通常需用到数形结合思想.在解答立体几何问题时,可先画出相应的几何图形;然后把数和形结合起来分析,根据图形的性质建立数量关系,或者把数量关系以图形之间的位置关系呈现出来,这样可使抽象问题具体化,能快速找到解题的思路.
例3.如图7,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,求点P到直线CC1的距离的最小值.
解:如图8,建立空间直角坐标系[D-xyz],
则[D1(0,0,2),E(1,2,0)],[C(0,2,0),C1(0,2,2)],
从正方体的结构特征出发,很容易建立空间直角坐标系,求得各个点的坐标,即可将立体几何问题转化为空间向量运算问题,从而通过数形之间的转化,快速求得最小值.
总之,在解答立体几何问题时,灵活运用数学思想,能有效地提升解题的效率.但是同学们需熟练掌握这些数学思想的特点、适用情形、用法以及注意事项,这样才能在解题时信手拈来.

