Fully asynchronous distributed optimization with linear convergence over directed networks*

,,

1. Department of Automation, Beijing National Research Center for Information Science and Technology, Tsinghua University, Beijing 100084, China

2. Beijing Sankuai Online Technology Co., Ltd., Beijing 100102, China

Abstract: We study distributed optimization problems over a directed network, where nodes aim to minimize the sum of local objective functions via directed communications with neighbors.Many algorithms are designed to solve it for synchronized or randomly activated implementation, which may create deadlocks in practice.In sharp contrast, we propose a fully asynchronous push-pull gradient(APPG) algorithm, where each node updates without waiting for any other node by using possibly delayed information from neighbors.Then, we construct two novel augmented networks to analyze asynchrony and delays, and quantify its convergence rate from the worst-case point of view.Particularly, all nodes of APPG converge to the same optimal solution at a linear rate of O(λk) if local functions have Lipschitz-continuous gradients and their sum satisfies the Polyak-Łojasiewicz condition (convexity is not required), where λ ∈(0,1) is explicitly given and the virtual counter k increases by one when any node updates.Finally, the advantage of APPG over the synchronous counterpart and its linear speedup efficiency are numerically validated via a logistic regression problem.

Key words: fully asynchronous; distributed optimization; linear convergence; Polyak-Łojasiewicz condition

1 Introduction

As data get larger and more spatially distributed, distributed optimization over a network of computing nodes (aka.agents or workers) has found numerous applications in multi-agent problems (Chang et al., 2015),machine learning (Assran et al., 2019), and resources allocation (Zhang et al., 2020b).It aims to minimize the sum of local objective functions, i.e.,

wherenis the number of nodes and the local objective functionfiis only known by nodei.Nodes are expected to solve (1) by only communicating with neighbors that are defined by the network.For example,fioften takes the formfi(x) ≔in empirical risk minimization problems(Assran et al., 2019), where Diis a local dataset of nodei,xis the model parameter to be optimized, andFi(x;ξ) is the loss of a single sampleξ.See Fig.1 for an illustration.

Fig.1 Undirected and directed peer-to-peer networks

For large-scale optimization problems, it is crucial to design an easily implementable algorithm that is robust to heterogeneous nodes and communication delays.Many existing works focus on synchronous algorithms where all nodes essentially start to compute each iteration simultaneously (c.f.Fig.2(a)) by using a global synchronization scheme that is often not amenable to the distributed setting.

Fig.2 （a） A synchronous algorithm over directed network；（b）A gossip-based algorithm； （c） A fully asynchronous algorithm

Asynchronous updates are demonstrated to perform better than the synchronous counterparts (Nedić, 2010;Lian et al., 2018; Wu et al., 2018; Xu et al., 2018; Assran et al., 2020; Zhang et al., 2020a).A popular one is gossip-based (Nedić, 2010; Lian et al., 2018; Xu et al., 2018) where a pair of neighbors is randomly selected to concurrently update via information exchange, see Fig.2(b).However, this may create deadlocks in practice(Lian et al., 2018), especially for networks with many cycles.It is also sensitive to communication delays and cannot work on directed networks.

To simultaneously address these issues, this work considers thefully asynchronoussetting (c.f.Fig.2(c)(Tian et al., 2020; Zhang et al., 2020a; Assran et al., 2021)) overdirectednetworks and proposes an asynchronous push-pull gradient (APPG) algorithm to distributedly solve (1).In APPG, a node starts to update without waiting for others with locally accessed (possibly stale) information.It does not need any network synchronization, and can tolerate uneven update frequencies and communication delays among nodes.

To theoretically evaluate its performance, we develop an augmented network approach and use the machinery of linear matrix inequalities (LMIs) to capture some key quantities via a novelλ-sequence.If all local functionsfihave Lipschitz continuous gradients and the global objective functionfsatisfies the Polyak-Łojasiewicz(PL) condition (no convexity requirement), we prove from the worst-case point of view that APPG converges linearly to an optimal solution at a rate O(λk), whereλ∈(0,1) is explicitly provided in terms of the asynchrony level and delay bounds, and the virtual counterkincreases by one no matter which node updates.Note that the convergence guarantee for gossip-based algorithms is generally given in the stochastic sense.

Then, we implement APPG on a multi-core server with the Message Passing Interface (MPI) to solve a multiclass logistic regression problem over theCovertypedataset.The result confirms that its empirical convergence rate in running time is faster than its synchronous counterpart, and achieves linear speedup efficiency with respect to the node number.Its robustness to slow computing nodes is also validated, which is essential in heterogeneous large-scale networks.

The rest of the paper is organized as follows.Section 2 briefly reviews related works.Section 3 formulates the problem and proposes APPG.We provide the theoretical guarantees for APPG in Section 4.To prove them,we first develop a time-varying augmented network approach in Section 5, and then establish the LMIs in Section 6.In Section 7, we conduct numerical experiments on APPG.Some concluding remarks are drawn in Section 8.

2 Related work

The past decade has witnessed an increasing attention on distributed optimization, especially for the design of synchronous algorithms over undirected networks, e.g., DGD (Nedić et al., 2009), DIGing (Nedić et al.,2017), NIDS (Jakovetić, 2019;Li et al., 2019; Sun et al., 2019; Yuan et al.,2019; Li et al.,2020; Xin et al.,2020; Yi et al., 2020; Xu et al., 2021).Extensions to directed networks while maintaining linear convergence are challenging due to the network unbalancedness.To resolve it, epigraph reformulation (Xie et al., 2018) and the push-sum-based method (Nedić et al., 2015; Assran et al., 2019; Scutari et al., 2019) have been proposed.For example, Push-DIGing (Nedić et al., 2017) combines the push-sum method and gradient tracking (Nedić et al., 2017; Xu et al., 2018) to achieve linear convergence for strongly convex and Lipschitz smooth functions over directed networks.However, it involves nonlinear operators per update and may cause numerical issues in implementation, which is resolved in the push-pull/AB algorithm (Xin et al., 2018; Saadatniaki et al., 2020; Pu et al., 2021) by simultaneously adopting a row-stochastic matrix and a column-stochastic matrix for information mixing.

In the meanwhile, asynchronous algorithms are proposed to alleviate the synchronization overhead.The gossip-based AsynDGM (Xu et al., 2018) assumes that each pair of neighbors is activated to update with a fixed probability, and has been extended in Lian et al.(2018) where the activated nodes admit a doubly-stochastic mixing matrix.Nedić (2010) considers that each node is activated by a Poisson process.More general models are studied in Zhao et al.(2015); Wu et al.(2018) by assuming nodes or edges are independently randomly activated with fixed probabilities.It is unclear whether these methods can be applied to directed networks especially when there exist communication delays.Moreover, the coordination between neighbors is indispensable.

Inspired by the seminal works (Tsitsiklis et al., 1986; Li et al., 1987), the fully asynchronous setting has emerged as a more scalable and easier implementable alternative.An ADMM-based asynchronous algorithm is studied in Chang et al.(2016) for the master-slave networks.For peer-to-peer networks, an initial attempt is made in Assran et al.(2021) to extend the synchronous gradient-push algorithm (Nedić et al., 2015) to the fully asynchronous setting.However, they cannot achieve exact convergence to an optimal solution if nodes have different update frequencies.To address it, Zhang et al.(2020a) proposes a novel adaptive mechanism to dynamically adjust stepsize, which is also adopted in Spiridonoff et al.(2020) to analyze stochastic algorithms.Nonetheless, the algorithms in Zhang et al.(2020a); Spiridonoff et al.(2020) only have sublinear convergence rates even if the objective function is strongly convex and Lipschitz smooth.Asy-SONATA (Tian et al., 2020) exploits the perturbed push-sum method with gradient tracking (Nedić et al., 2017; Xu et al., 2018) in the fully asynchronous setting, which converges linearly for strongly convex problems and sublinearly for non-convex problems.The differences between Tian et al.(2020) and our work include: (i) APPG further converges linearly even under the PL condition, which holds for some important non-convex problems, e.g., the policy optimization for LQR(Fazel et al., 2018).(ii) APPG uses uncoordinated constant stepsizes while Asy-SONATA can only use uncoordinated diminishing stepsizes, which however leads to a sublinear convergence rate.(iii) We provide explicit convergence rate for APPG in terms of key parameters of the problem, while an explicit rate seems unclear for Asy-SONATA.

Notation: We use the following notations:

(i) [A]ijdenotes the element in rowiand columnjofA.|A| denotes the cardinality of set A.denotes the largest integer less than or equal tox.Rnand N denote the set ofn-dimensional real numbers and natural numbers, respectively.

(ii) ‖ · ‖2denotes thel2-norm of a vector or matrix.‖ · ‖Fdenotes the matrix Frobenius norm.O(·) denotes the big-O notation.

(iii) 1nand 0ndenote respectively then-dimensional vector with all ones and all zeros.The subscript may be omitted if the dimension is clear from the context.

(iv) ∇f(x) denotes the gradient of a functionfatx.

(v)ais called a stochastic vector if it is nonnegative andaT1 = 1.Ais called a row-stochastic matrix ifAis nonnegative andA1 = 1.Ais column-stochastic ifATis row-stochastic.

(vi) [a1,a2,…,an] and [a1;a2; …;an] denote the horizontal stack and vertical stack ofa1,a2,…,an, respectively.

(vii) ΠX(x) denotes the projection ofxonto the setX.

3 Problem formulation and the APPG

3.1 Problem formulation

We aim to solve (1) over a directed network (digraph), which is denoted by G =(V,E), where V ={1,2,…,n}is the set of nodes and E ⊆V × V is the set of edges.The directed edge (i,j) ∈E if nodeican directly send information to nodej.Let={j|(j,i) ∈E }∪{i} denote the set of in-neighbors of nodeiand={j|(i,j) ∈E }∪{i} denote the set of out-neighbors ofi.A path from nodeito nodejis a sequence of consecutively directed edges from nodeito nodej.Then, G isstrongly connectedif there exists a directed path between any pair of nodes.

For a distributed algorithm over G, each nodeihas a local state vectorxiand iteratively update it via directed communications with neighbors, the objective of which is to ensure that all local statesxi,i∈V converge to an optimal solution of (1).In this work, we make the following assumptions.

Assumption 1

(a) The digraph G is strongly connected.

(b) All local functionsfiareβ-Lipschitz smooth, i.e., there exists aβ＞0 such that

(c) The global objective functionfhas at least one minimizer and satisfies the Polyak-Łojasiewicz condition(Karimi et al., 2016) with parameterα＞0, i.e.,

wheref⋆=

Assumptions 1(a)-(b) are standard in the distributed smooth optimization over directed networks (Nedić et al., 2017; Pu et al., 2021).The PL condition in Assumption 1(c) is satisfied in some importantnon-convexproblems such as the policy optimization for LQR (Fazel et al., 2018).It is strictly weaker than the strongly convex condition that is commonly used to derive the linear convergence of gradient-based methods (Nedić et al.2017;Tian et al., 2020).Particularly, the strong convexity implies the uniqueness of the minimizer, which is clearly not the case for the PL condition.

3.2 The APPG

We propose APPG to solve (1), which is given in Algorithm 1 from the view of a single node.Note that we do not introduce any iteration index to emphasize the fact of fully asynchronous implementation.

① In-neighbors include i itself，i.e.， x͂i and y͂i are copied to Xi and Yi ；② The average can be weighted，e.g.， one may assign higher weights to more recent messages to potentially improve the convergence rate in practice.

Our novel idea lies in the use of local buffers to achieve asynchronous updates.Particularly, a node just keeps receiving messages from its in-neighbors and storing them to its local buffers until it is activated to compute a new update via (2), which involves only summation and (weighted) average of data in the buffers, and a local gradient computation.Clearly, each buffer may contain zero, one or multiple receptions from the same inneighbor, which is unavoidable in the fully asynchronous setting.Another feature of APPG is that the node computes a new update by using all messages in the buffers instead of only using the latest reception (Tian et al.,2020).This enables APPG to be robust to bounded communication delays, out of sequence issues and there is no need to use time-stamps (Tian et al., 2020).Note that APPG can also use only the latest information by carefully assigning weights to receptions.In addition, the local buffers are only conceptually needed and can be waived in implementation since the average and summation operators in (2) can be recursively computed.After (2), the node broadcasts the updated vectors to its out-neighbors and discards all the used messages.Such a process is repeated until a local stopping criterion is satisfied.

Different from synchronous or gossip-based algorithms, APPG does not require any global clock or coordination among neighbors, and each node does not wait for others for new updates.For example, a node can simply start to compute a new update once it completes the current one or receives a message.Thus, there is no deadlock problem.Moreover, nodes do not need to use the same stepsize.

3.3 The idea of APPG

This subsection aims to intuitively explain the linear convergence of the APPG.To this end, we first show how APPG works if nodes are forced to update synchronously.In this case, we can use a global iteration indexkto record the update progress.

LetX(k),Y(k) and ∇f(X(k)) be the stacked local states and gradients at thek-th iteration, i.e.,

andΓ= diag(γ1,…,γn).Then, we obtain that

where the row-stochastic matrixAand column-stochastic matrixBresult from avg(·) and sum(·) in (2), respectively.Clearly, (3)-(4) reduces to the algorithm(Xin et al., 2018; Saadatniaki et al.,2020;Pu et al.,2021), which has been proved to converge linearly for strongly convex and Lipschitz smooth functions.

The key to the linear convergence of (3)-(4) is the introduction ofyito distributedly track the gradient off.To see it, we left multiply (4) with 1T, use the column-stochasticity ofBand noticeY(0) = ∇f(X(0)).This implies that

Now suppose thatX(k) andY(k) have already converged toX∞andY∞, respectively.It follows from (4) thatY∞=BY∞.Jointly with (5), we obtain that

where πBis the Perron vector ofB, i.e.,BπB= πB.Moreover, the row-stochasticity ofAimplies thatX∞=1(x∞)Tand

Let πAbe Perron vector ofAT.We left multiply (6) with (πA)Tand notice thatX∞= 1(x∞)T.Then,

whereρ=(πA)TΓπBand=(πA)TX(k+ 1).Clearly, (7) is a gradient descent update, which converges linearly under Assumption 1.It also shows that the limiting pointx∞must be an optimal pointx⋆andyiconvergesMoreover, the smaller theyi, the closerxito an optimal solution.Therefore,yican serve as a stopping criterion in Algorithm 1.

In the fully asynchronous setting,yiplays a similar role.However, a theoretical understanding of APPG is much more complicated.The information delays make the key relation (5) invalid and the uncoordinated updates degrade the tracking performance ofyi.In essence, APPG is a multi-timescale decision-making problem.To resolve it, we develop an augmented network approach to prove its linear convergence by associating each node with some virtual nodes, under which the asynchronous updates and communications of nodes are transformed into synchronous operations over the augmented network.Moreover, the key technique(Xin et al., 2018; Saadatniaki et al., 2020;Pu et al., 2021) cannot be applied since the transformed system is time-varying and lacks important properties(e.g.the irreducibility of the weighting matrix).To this end, we further introduce an absolute probability sequence and aλ-sequence for the proof.

4 Linear convergence of APPG

Two assumptions on the asynchrony and communication delays are needed for the convergence of APPG.

Assumption 2(Bounded activation time interval) Lettiandbe any two consecutive activation time of nodei.There exist two positive constantsandsuch that

Assumption 2 is easily satisfied and desirable in practice.In fact, both the lower and upper bounds exist naturally since computing update consumes time and can be finished in finite time.If violated, e.g., some node is broken, then the information from this node can no longer be accessed, and hence it is impossible to find an optimal solution of (1).

Assumption 3(Bounded transmission delays) For any (i,j) ∈E, the transmission delay from nodeito nodejis bounded by a constantτ＞0.

Note that transmission delays can be time-varying, and the parametersandτare not needed for implementing APPG.

Let T ={t(k)}k≥1be an increasing sequence of updating time of all nodes, i.e.,t∈T if some node starts to update at timet.Denote the state of nodeijust before timet(k) byxi(k) andyi(k).Then, the following lemma introduces an important quantitybto characterize the information delay in terms of T.

Lemma 1The following statements hold.

(i) Under Assumption 2, letb1=(n- 1)+ 1.Each node is activated at least once within the time interval (t(k),t(k+b1)].

(ii) Under Assumptions 2-3, letb2=andb=b1+b2.The information sent from nodeiat timet(k)can be received by nodejbefore timet(k+b2) and used to compute an update before timet(k+b) for anykand(i,j) ∈E.

Proof(i) Suppose that nodeiis not activated during the time interval (t(p),t(q) ],p,q∈N but is activated att(q+ 1).It follows from Assumption 2 thatt(q) -t(p) ≤Moreover, any other node can be activated attimes during the time interval (t(p),t(q) ], which impliesq-p≤(n- 1)Hence, the first part of the result follows.

(ii) Suppose that nodeisends information at timet(p),p∈N and nodejreceives it in the time interval(t(q),t(q+ 1) ],q∈N.It follows from Assumption 3 thatt(q) -t(p) ≤τ.Moreover, Assumption 2 implies that any node can be activated at mosttimes during the time interval [t(p),t(q)], i.e.,q-p+ 1 ≤and henceq+ 1 ≤p+The result follows by lettingp=k.Jointly with Lemma 1(i), the rest of proof follows immediately.

The quantitybmeasures the largest possible information staleness caused by asynchrony and delays.For synchronous algorithms without communication delays, we haveb= 1.For cyclic updating modes where nodeiupdates att(nl+i),∀l∈N, we can setb=n.Note that a largerbdoes not imply that the algorithm updates slower in wall-clock time.For example,bis small in synchronous algorithms butt(k+ 1) -t(k) may be large due to idle time, while in fully asynchronous algorithmsbis often large butt(k+b) -t(k) can be small.Our main theoretical result is given below.

where

α,βare given in Assumption 1,bis defined in Lemma 1, andθ=(nb)-nb.

Theorem 1 shows that the local decision vector of each node in APPG converges to the same optimal solution at a linear rate, which is characterized in terms of key parametersn,b,α,βandγi.The quantityθin Theorem 1 reflects the speed of achieving consensus and depends on the network topology and asynchrony.Letbe the maximum difference among nodes at timet(k), then we can show thatv(k+nb) ≤(1 -θ)v(k) when applying APPG on the consensus problem withfi= 0, ∀i.Clearly, the convergence rate of APPG cannot exceed the consensus speed, which is reflected in the first term of the left-hand-side of (9).

To obtain a deterministic convergence rate, Theorem 1 adopts theworst-casepoint of view under the setting that: (a) The underlying network is heavily unbalanced, i.e., the differences between the numbers of inneighbors and out-neighbors of a node is large.(b) Some nodes compute much faster than the others (match the lower and upper bounds of Assumption 2, respectively).(c) Communication delays are based on the upper bound in Assumption 3.The values ofbandθin Lemma 1 and Theorem 1 are given in this case.Thus, the theoretical rate is expected to be very conservative, but the practical performance is empirically much better.For the synchronous delay-free case, we haveb= 1 andθ=n-n, and the convergence rate in Theorem 1 reduces towhere the first term in max( · ) matches the consensus result in Olshevsky et al.(2011, Theorem 8.1), and the second term is close to the push-pull method (Pu et al., 2021, Remark 6).

Note that the virtual counterkin (8) increases by one no matter which node updates, and hence more nodes generally lead to faster increase ofk.To some extent, this suggests a linear speedup efficiency of APPG, which is confirmed via experiments in Section 7.

5 The time-varying augmented system

This section develops our time-varying augmented network approach for the convergence analysis.

5.1 Construction of the augmented digraph

Let Ti⊆T be the sequence of activation time of nodei, i.e.,t∈Tiif nodeicomputes an update at timet.Then, it is clear that

To handle bounded time-varying transmission delays and asynchrony, we associate each nodeiwith two types of virtual nodes, and each type hasbvirtual nodes, wherebis given in Lemma 1(ii).We denote the above two types of virtual nodes byandrespectively.We call the first type virtual nodesxtype nodes, which is to deal with the staleness of the state,i∈V.The second type with subscriptyis calledytype nodes, which is to handle the staleness of,i∈V.Then, we construct an augmented time-varying digraphto represent the communication topology of all these nodes at timet(k), where V͂ containsn(2b+ 1) nodes, includingnnodes of G and 2nbvirtual nodes.

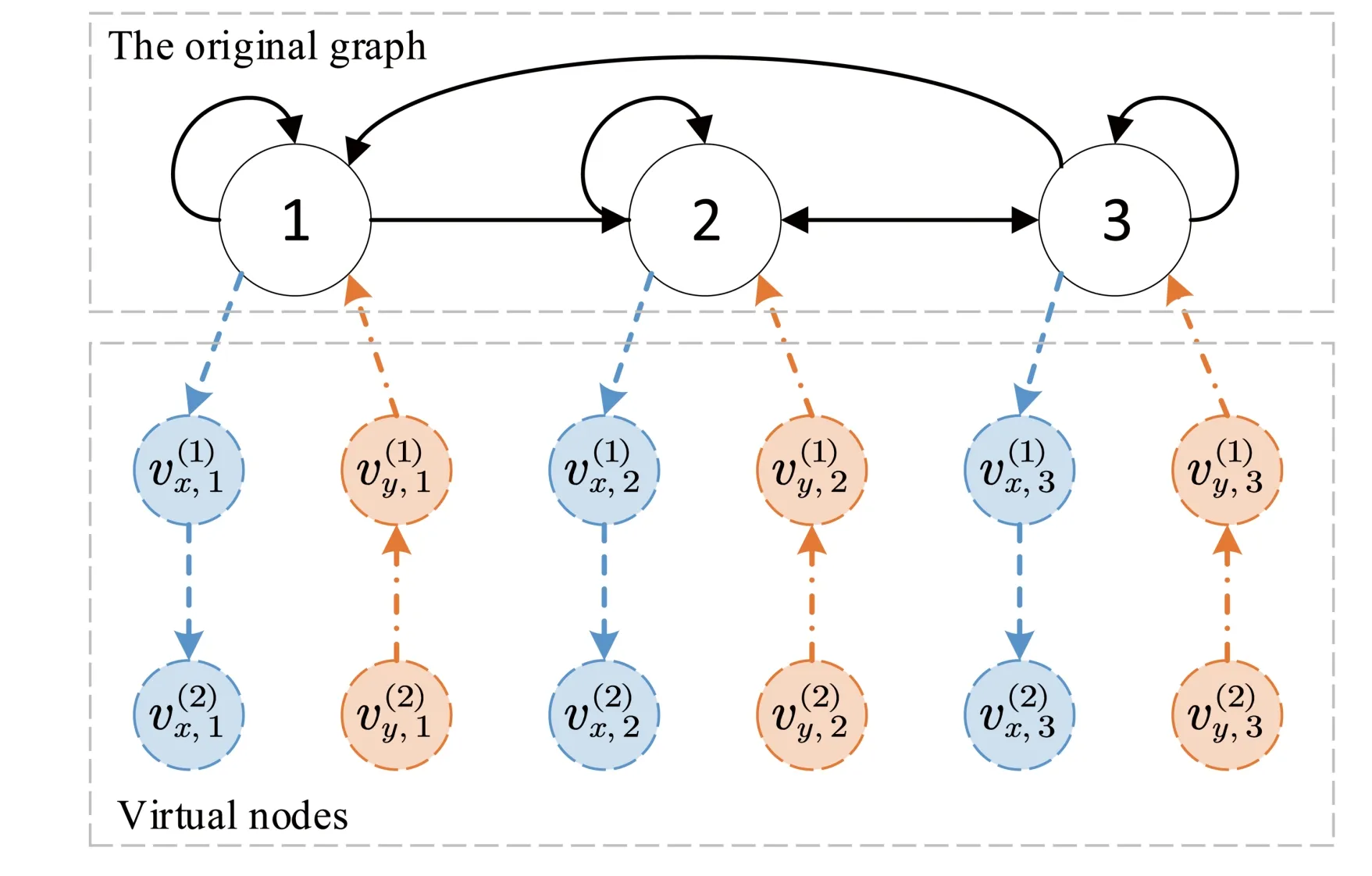
Fig.3 An augmented graph with virtual nodes to address delays of the original graph

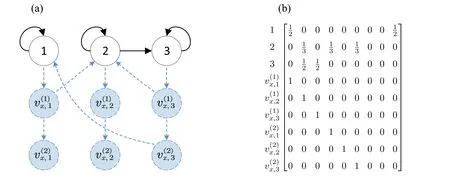
Fig.4 (a) The topology of the x-type virtual nodes in the augmented graph at some time t(k);(b) The corresponding row-stochastic matrix

Fig.4(a) illustrates such an augmented graph①The idea of adding virtual nodes to address asynchrony or delays was firstly adopted in Nedić et al.(2010) to study consensus problems and in Zhang et al.(2020a); Tian et al.(2020); Assran et al.(2021) for distributed optimization.Nevertheless, Nedić et al.(2010);Zhang et al.(2020a); Assran et al.(2021) use only x-type virtual nodes and involve division operators.We further introduce y-type nodes to accommodate linear update rules.Tian et al.(2020) associates virtual nodes to original edges rather than original nodes.Since there are generally more edges than nodes in a strongly connected graph and the theoretical convergence rate becomes slower as the number of virtual nodes increases, our analysis may potentially be sharper than Tian et al.(2020).at some timet(k), where node 1 uses the 2-steps delayed informationand the latest informationto computex1(k), and henceNode 2 usesand the 1-step delayed informationandto computex2(k).Node 3 use the latest informationandto computex3(k).The corresponding row-stochastic matrixis as demonstrated in Fig.4(b).

The topology of they-type virtual nodes is similarly developed with reversed edge directions (c.f.Fig.5(a)),which is the main motivation of using two types of virtual nodes.Firstly, edges,…, andare always included inwith the reversed directions ofx-type nodes, see Fig.3.Secondly, if(i,j) ∈E in G andk∈Ti, then only one edge in edgesand (i,j) is included in E(k),which also depends on the transmission delay ofsent from nodeito nodej.At timet(k), suppose that nodeisendsyi(k) to nodej, which is received att(k+u) foru＞1, thenand the delay isu- 1.Similarly, if there is no communication delay, i.e.,u= 1, then (i,j) ∈Fig.5(a) illustrates such an augmented graph at some timet(k), which represents that node 1 sendsto node 2 and node 2 use it att(k+ 3) to computey2(k+ 3).Other edges can be interpreted similarly.The corresponding column-stochastic matrixis as depicted in Fig.5(b).

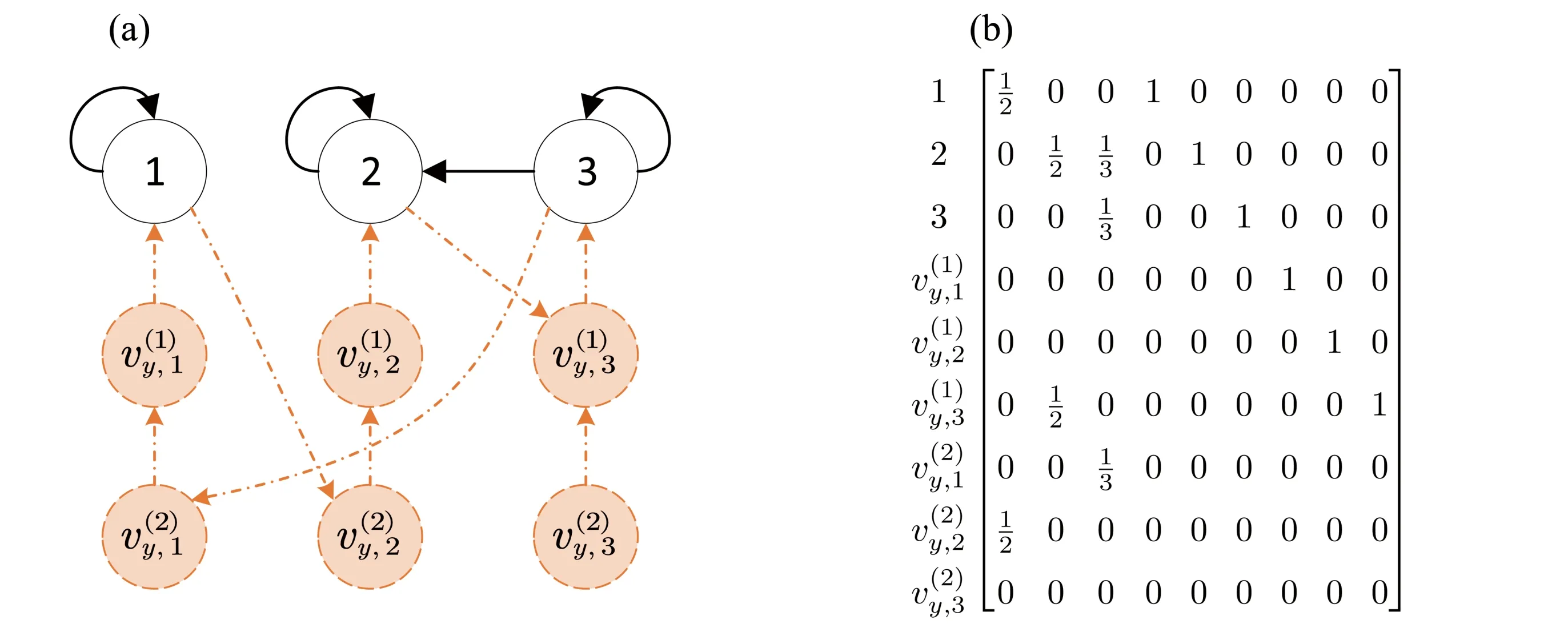
Fig.5 (a) The topology of the y-type virtual nodes in theaugmented graph at some time t(k) ;(b) The corresponding column-stochastic matrix

We provide a simple example to visualize the augmented graph approach.Consider that nodeisendsandto nodejat timet(k), and nodejreceives it at timet(k+ 2), i.e., the delay is 1.In the augmented graph, this can be viewed as nodeidirectly sendsto the virtual nodeand sendsto the virtual nodeat timet(k).Nodesandrespectively receiveandat timet(k+ 1), and immediately send them to nodejat timet(k+1).Finally, nodejreceivesandat timet(k+2).Clearly, all non-virtual nodes in͂receive the same information as that in G and hence their updates appear to be synchronous and delay-free.

Under the time-varying augmented digraph, we are able to rewrite the APPG in a compact form.

5.2 A compact form of the APPG over the augmented digraph

where |Xi(k)| is the number of elements in the buffer Xiat timet(k+ 1).

which is obtained by left multiplying the second equality of (10) with.

Note that (10) generates the same sequence of the statesxiandyias that of APPG.Hence, it is sufficient to study the convergence ofandin (10).To this end, we define

wherek,t∈N, and we adopt the convention that=Iand= 0 for anyk∈N andt＜0.

The following lemma states thatandlinearly converge to rank-one matrices.

Lemma 2Under Assumptions 1-3, the following statements are in force.

(i) Letθbe the minimum nonzero element ofandIt holds that≤θ＜1, wherebis defined in Lemma 1(ii).

(ii) There exist stochastic vectorsandsuch that

for allk,t∈N, whereρ=(1 -θ)1/n͂＜1.

ProofPart (i): In view of (12) and (13), the minimum nonzero element ofandis greater than 1/n͂ for allk.Thus, the minimum nonzero element ofandis greater thann͂-tfor anyt＞0.

Part (ii): In view of Lemma 1, bothandare indecomposable for allk, and thus ΦAnb(k) andhave positive columns.Then, the proof is similar with that Lemma 5 (Nedić et al., 2010) or Lemma 3(Nedić et al.,2015), and we omit it for saving space.

Part (iii): We study two cases separately.Ift＜b, then

Ift≥b, it follows from a similar argument with the Lemma 2(ii) in Nedić et al.(2010) that [Φb(k)]ij≥n-bfor alli∈V andj∈V͂.Then,

where the last inequality follows from the column-stochasticity ofThe desired result is obtained by induction.

The following lemma is a direct result of Lemma 2, which specifiesμandt͂ used later.

ProofIn view of Lemma 2(ii), it can be readily checked that (16) satisfies.We have

Finally, we introduce theabsolute probability sequence(Touri, 2012).

Lemma 4(Theorem 4.2 in Touri (2012)) For a sequence of row-stochastic matrices {A(k)}, there exists a sequence of stochastic vectors {π(k)} satisfying

{π(k)} is called an absolute probability sequence of {A(k)}.

In the sequel, we useπ(k) ∈Rn͂to denote an absolute probability sequence ofwhich implies that

6 Proof of Theorem 1 via LMIs

Under the augmented time-varying digraph, we are ready to prove Theorem 1.

6.1 Outline of the proof

As Nedić et al.(2017), for a nonnegative sequence {p(k)}, we define that

forλ∈(0,1).We call {pλ,k} theλ-sequence ofp(k).Clearly, ifpλ,kis uniformly bounded by some constantc,thenp(k) ≤cλkfor allk.Our method to prove Theorem 1 is to show the boundedness ofpλ,k,k∈N in (18) for some nonnegative sequencesp(k).Under Assumptions 1-3 and (10), the proof of Theorem 1 relies on the following four lemmas, whose proofs are given in next subsections.

Lemma 5Let

Proof of Theorem 1

Note thatλandγi,i∈V defined in Theorem 1 satisfy all the conditions onλin the above four lemmas and the condition onγiin Lemma 7.Thus, (19), (21), (23) and (24) hold.Let

Combining (19), (21), (23), and (24), we obtain that for allk∈N,

where ≼ is the element-wise inequality andMis a nonnegative matrix

6.2 Two useful propositions

We establish two important results in this subsection.The first one shows a property ofλ-sequence and the second one recalls the contraction relation of gradient methods.

Proposition 1Let {p(k)},{q(k)} be nonnegative sequences satisfying

wherer∈[0,1).If we chooseλsuch thatλj∈(r,1), then theλ-sequencespλ,kandqλ,kin (18) satisfy

It follows from (26) that

This giveskinequalities by selectingt= 1,…,k.On the other hand, we haveλ-t p(t) ≤λ-t p(t), which gives anotherjinequalities by selectingt= 1,…,j.Take the maximum on both sides of thesek+jinequalities and use the definition ofλ-sequence, we obtain

Ifλj∈(r,1), then (27) implies

for allk+j∈N, where we have used that 1 -λj≤j(1 -λ).The result is obtained immediately.

For any nonnegative sequences {p(k)}, {q(k)}, lettingr(k) =p(k) +q(k), it holds thatrλ,k≤pλ,k+qλ,k,which can be easily checked by definition.

The following proposition shows the convergence rate of a perturbed gradient descent method for minimizing functions satisfying the PL condition.As a special case, it recovers the linear convergence rate of the standard gradient descent method.

6.3 Proof of Lemma 5

6.4 Proof of Lemma 6

6.5 Proof of Lemma 7

6.6 Proof of Lemma 8

7 Numerical examples

We use APPG to train a multi-class logistic regression classifier in a distributed manner on theCovertypedataset (Dheeru et al., 2017), where the objective function takes the following form

Herens= 581 012 is the number of training instances,nc= 7 is the number of classes,nf= 55 is the number of features,si∈R55is the feature vector of thei-th instance,is the label vector of thei-th instance using the one-hot encoding,X=[x1,…,x7]∈Rnf×ncis the parameters to be optimized,ρ= 20 is a regularization factor.

Environment:APPG is implemented in Python with OpenMPI 1.10 on Ubuntu 14.04.The hardware is a server with 28 Xeon E5-2660 cores.Each core serves as a computing node.

Distributed Data:We first normalize non-categorical features by subtracting the mean and dividing by the standard deviation in the whole dataset.Then, wesortthe data by digit label, and sequentially partition it intonparts (with different sizes), where each node (core) only hasexclusiveaccess to one part.Thus, we are dealing with distributed datasets.

Topology:The directed network among nodes is as follows: Each nodeisends messages to node mod(2j+i,n), wherej∈N ∩[0,log2(n)) and mod(a,b) returns the remainder after division ofabyb.Thus, each node has O(log(n)) out-neighbors, which results in a relatively sparse directed networks.Note that gossip-based asynchronous algorithms are generally not applicable over this directed network.

Stepsize:The stepsize of each algorithm is tuned via a grid search around 0.5/ns.

Local Termination Criteria:Nodeistops locally if the values ofyiin lastnconsecutive iterations are less than 300/ns.

7.1 Convergence performance and linear speedup

We implement APPG overn= 1, 6, 12, 18, 24 nodes (n= 1 is used as a baseline since APPG reduces to standard centralized gradient descent method).The training loss w.r.t.running time is plotted in Fig.6(a), which validates the linear convergence of APPG, and shows that the training time is significantly reduced with the increase of number of nodes.

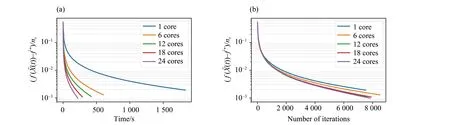
Fig.6 Convergence performance with different number of nodes.(a) Training loss w.r.t.running time of APPG;(b) Training loss w.r.t.number of iterations of APPG

Fig.6(b) depicts the training loss w.r.t.the number of iterations.We find that the number of iterations required to achieve the same accuracy is close to each other for different number of nodes.The time for a node to finish an iteration is proportional to the size of its local dataset, and hence is roughly inversely proportional to the number of nodes, which suggests that usingnnodes may reduce O(n) times of training time than that of one node.

To further illustrate this property, we study the speedup of APPG defined asSn≔Tn/T1, whereTnis the running time of the APPG withnnode (s) when the training loss decays to 0.005.Fig.7(a) shows that the APPG achieves a roughly linear speedup in convergence rate w.r.t.the number of nodes.Then, we test a synchronized version of APPG, which is done by adding a barrier after each update and is mathematically equivalent to the push-pull method in Pu et al.(2021).One can find that the synchronous version has an approximately linear speedup when the number of cores is small, but it decreases fast when the number of cores is relatively large.

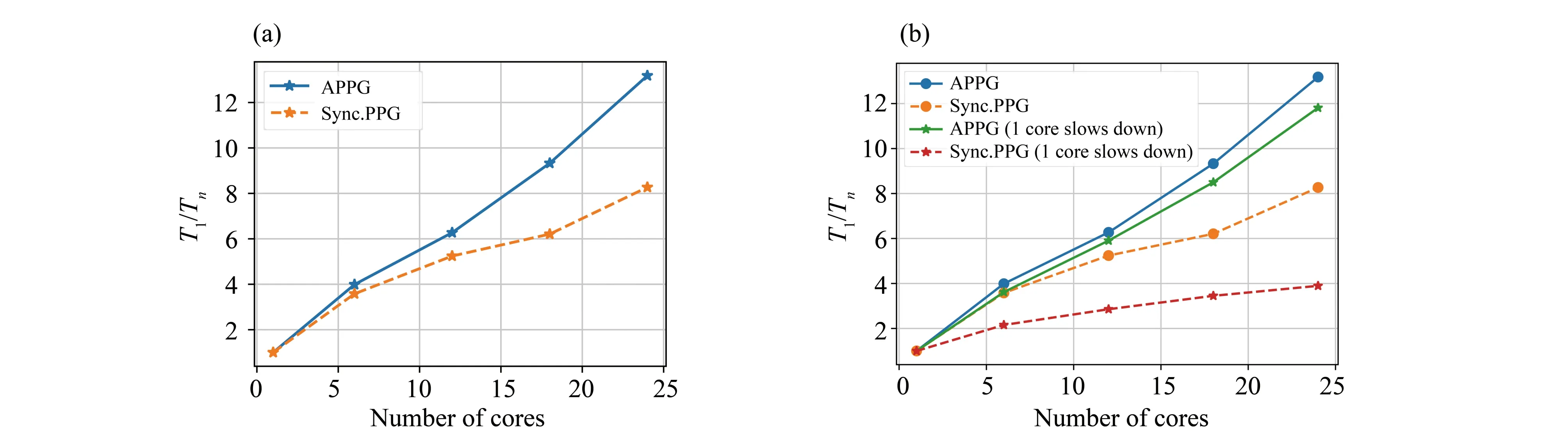
Fig.7 (a) Speedup of APPG and the synchronous implementation of APPG;(b) Speedup of APPG and the ‘synchronized’ APPG with one slow core

Ideally, the speedup would benwhen usingnnodes.However, the communication among nodes introduces delays and staleness to the algorithm, which degrades the convergence rate.In practice, a higher speedup can be achieved by using a lower latency network with larger bandwidth.

7.2 Robustness of APPG to slow cores

We evaluate the robustness of APPG by forcing one core in the network to slow down.This is achieved by adding an artificial waiting time (20 ms, a normal iteration takes about 15 ms with 24 cores) after each local iteration of a node, which simulates either the slow computation or slow communication.

Fig.7(b) shows the speedup of APPG and the synchronous implementation of APPG in this scenario.It indicates that the synchronous counterpart of APPG has a sharp reduction in convergence rate even when only 1 core slows down.In contrast, APPG still keeps an almost linear speedup.This result is also consistent with that in Lian et al.(2018); Zhang et al.(2020a).

Introducing the slowing core also brings an essential problem of asynchronous algorithms, that is, the cores haveunevenupdate rates.To show its effect to the performance, we compare APPG to a gossip-based asynchronous algorithm AD-PSGD (Lian et al., 2018) with full local gradients.Note that APPG can only work overundi‐rectednetworks, and hence we modify the network by adding a reversed edge to each edge in the directed network, while APPG is still implemented over the directed network.Fig.8 shows the result over 12 nodes and 24 nodes, where AD-PSGD fails to converge to the exact optimum.In contrast, APPG converges exactly despite a bit slower convergence rate.

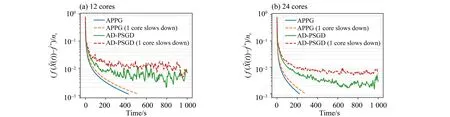
Fig.8 Convergence of APPG and AD-PSGD with full local gradient when one node is artificially slowed down.

8 Conclusion

This paper has proposed APPG for distributed optimization which allows nodes to connect via a directed communication network and update with uncoordinated computation and stale information from neighbors.Future works may focus on accelerating APPG and extending it to stochastic optimization.