充填节理特性对岩石静态压缩力学行为影响的颗粒流模拟*

宋浪， 柴少波，， 宋博阳， 柴连增， 杜宇翔

1.长安大学建筑工程学院，陕西 西安 710064

2.江汉大学爆破工程湖北省重点实验室，湖北 武汉 430056

实际工程岩体中随机分布着大量的节理，而节理往往含有一定的充填物。相比于非充填节理，充填节理由于裂隙贯通性好、充填材料强度低等特点，其力学强度和变形特性更差。在外荷载作用下充填节理层容易产生法向及切向变形，进而易引起节理岩质边坡或地下洞室工程失稳破坏。因此，研究荷载作用下充填节理岩石的力学及变形特性可为节理岩体工程稳定性分析和安全性评价提供指导。

近年来对充填节理岩石力学及变形特性的相关研究持续升温（Li et al.，2014；史玲等，2012；Liu et al.，2017）。Li et al.（2009）利用改进的SHPB装置研究发现充填节理的含水量和厚度对充填节理岩石动态应力-应变曲线有明显的影响。刘婷婷等（2017）采用RMT-150C试验机进行充填节理的直接剪切试验，研究了法向压力、剪切速率和充填厚度对其剪切力学特性的影响。许江等（2021）研究了循环荷载作用下充填厚度对结构面剪切力学特性和破坏模式的影响。肖维民等（2019，2020）研究了节理粗糙度和充填度对薄层充填岩石节理抗剪强度、剪胀特性和破坏特征的影响。Chai et al.（2020）研究了不同充填厚度及不同充填材料对节理岩石试样静态和动态力学特性的影响，研究发现充填节理的静态和动态抗压强度，随节理充填物强度的增大而增大，随节理厚度的增大而减小；静态和动态压缩下充填节理的变形特性与充填物材料性质相关。此外柴少波等（2020，2022）还进一步研究了累积冲击和干湿循环作用对充填节理岩石力学特性的影响规律，一定程度上揭示了劣化作用下充填节理岩石力学特性的损伤规律。

以上研究均采用室内物理试验的方法，但由于室内试验中人工制备充填节理岩石试样成本高、养护周期长且试样制作精度存在差异，故室内物理试验存在一定的难度。此外，近年来随着计算机技术的迅速发展，基于离散元法的数值计算软件PFC 从散体介质的微观力学特征出发，构建的数值模型可以真实逼近岩石材料的力学特性，反映节理岩体的非线性大变形特征，在模拟节理岩体此类非均质、非连续材料方面具有很大的优势（王卫华等，2005），受到了许多研究人员的青睐。例如，Zhang et al.（2012；2013）利用PFC2D程序研究了单轴压缩过程中裂隙倾角对单裂隙和双裂隙岩石裂纹扩展情况的影响。金爱兵等（2012）进行了岩石的双轴试验模拟，从岩桥长度、节理长度和节理倾角三方面对岩石的破裂模式和力学特性进行了分析。黄彦华等（2014，2015）采用PFC2D研究了不同围压作用下含共面双裂隙脆性砂岩的强度变化情况和裂纹演化规律，此外还研究了节理数量、节理倾角和围压对含两组交叉节理岩体强度及破坏特征的影响。周喻等（2012）从宏观和细观角度深入探讨了节理在直剪试验过程中的力学演化规律和破坏机制。张国凯等（2016）进行了单轴压缩下节理厚度和刚度比对试件宏观力学参数、能量及波传播规律影响的数值模拟，但缺乏与室内物理试验结果的对比验证。许万忠等（2018）进行了直剪试验数值模拟，研究JRC 系数、充填强度、接触面黏结强度等参数对充填节理剪切强度的影响。连莲等（2019）研究了不同充填厚度下充填节理的剪切破坏行为和强度特性。综上所述，现有文献关于节理岩石的颗粒流数值模拟中研究对象多为非充填节理，针对充填节理岩石的数值模拟研究较少，且其中剪切力学特性的研究居多，而压缩力学特性的研究较为匮乏。

鉴于此，本文开展充填节理特性对岩石静态压缩力学行为影响的颗粒流模拟。首先在PFC2D程序中构建充填节理岩石数值模型，根据充填节理岩石的室内物理静态单轴压缩试验结果进行细观参数标定及合理性验证，其次进一步研究不同节理倾角、多条节理数以及不同节理厚度情况下充填节理岩石的力学参数变化规律、微裂纹扩展和破坏形态情况。研究成果可丰富充填节理力学特性研究，并为复杂分布充填节理岩体工程稳定性分析提供参考。

1 数值模型建立及验证

本文前期研究（柴少波等，2022）的室内静态单轴压缩试验，所用充填节理岩石试样直径为50 mm、高为35 mm（图1）。为对比需要，本文在PFC中建立相同尺寸的数值模型（图2）。

图1 充填节理岩石实物图Fig.1 Photos of filled jointed rock samples

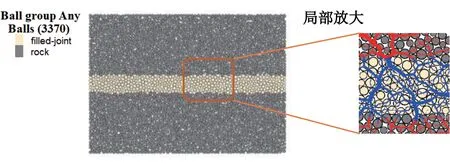
图2 充填节理岩石颗粒流数值模型Fig.2 Particle flow numerical model of filled jointed rock

PFC 程序中内置接触模型有多种：线性模型、接触黏结模型、平行黏结模型、平直节理模型和光滑节理模型等，其中平行黏结模型可以很好地模拟岩石材料的力学行为（黄彦华等，2014；LEE et al.，2011），本数值模型采用平行黏结模型。平行黏结模型包括两种接触界面：其一是无限小的线弹性界面，该界面可以承受摩擦力，但无法承受张力和传递力矩，该界面模型等效于线性模型；其二是有具体尺寸的线弹性黏结界面，可以传递力和力矩，称之为平行黏结。当第二种界面黏结时，能抵抗扭矩且表现为线弹性，当所受的作用力大于强度极限时，黏结模型失效，从而无法传递荷载，退化为线性模型。此外，由于数值模型中颗粒粒径大小和数量会对宏观力学参数产生一定影响（周喻等，2011），所以需要考虑模型最小尺度上颗粒数RES（resolution）对宏观参数的影响，官方Itasca建议RES＞20，并定义

式中L为数值模型的最小尺度，Rmax为颗粒最大粒径，Rmin为颗粒最小粒径。

考虑计算效率和文献中颗粒粒径的选取（阿比尔的等，2018；田文岭等，2017；黄达等，2013），本文设置中Rmin=0.3 mm，Rmax=0.5 mm，根据式（1）计算得到本数值模型RES=43.9，满足RES＞20的要求。数值模型共生成了颗粒3 370个，接触7 675个，孔隙率为1.2%，颗粒密度为2 700 kg/m³。为了准确模拟室内静态单轴试验的加载过程，上下墙的速度设定为0.05 m/s（田文岭等，2017；杨圣奇等，2022），当应力跌至峰值应力的70%时停止加载。

细观参数标定是建立准确的颗粒流数值模型的关键，微观参数标定是一个非常繁杂的过程，PFC 软件推荐使用“试错法”进行细观参数标定，“试错法”本质上就是通过不断调试细观参数，使得数值模拟结果和实际物理试验结果接近，从而达到逼近宏观试验的目的。在细观参数标定过程中需综合考虑充填节理岩石试样以及各自分层的力学参数，岩石层和充填节理层细观参数的比例关系参考实际物理实验两者力学参数的比例关系。此外由于实际工程岩体中的节理充填层是由岩石碎屑分化形成的颗粒与具有一定黏性的矿物胶结形成的混合物，在沉积作用过程中节理充填层与岩石会存在一定的黏结力，且黏结力的大小与节理充填层内部的黏结力基本相同。故本数值模型中岩石层和充填节理层之间的接触也采用平行黏结模型，其细观参数与充填节理层组内颗粒间接触的细观参数保持一致。本研究中充填节理岩石数值模拟与室内物理试验的应力-应变曲线对比结果如图3（a）所示。可以看出，数值模拟与室内试验的单轴压缩应力-应变曲线除了前期不同，后期相似度很高，这是由于PFC2D程序中数值模型在初始状态时通过伺服机制使得模型已经达到了密实状态，故无法模拟压缩过程中岩样的初始压密阶段（黄彦华等，2015；张宝玉等，2021；于利强等，2021）.所以在进行数值模拟结果和室内试验结果比较分析时，忽略室内试验压密阶段充填节理层产生的压密变形量，主要对比峰值应力和弹性阶段时弹性模量的差异以及最终破坏形态。数值模拟与室内物理试验压缩破坏形态结果对比如图3（b）所示，可发现数值模型的最终破坏形态与实际物理试验充填节理岩石的破坏形态较为吻合。

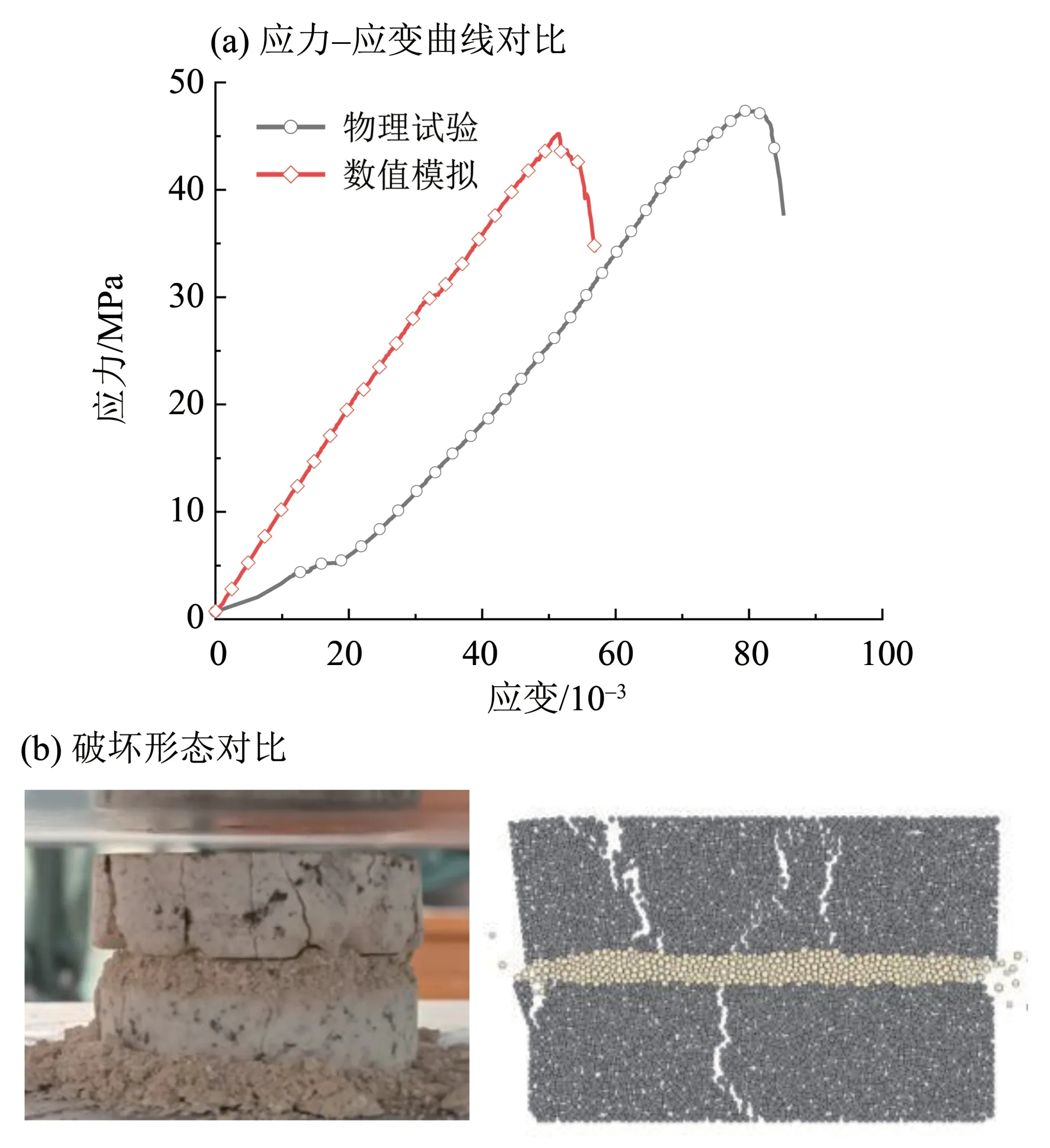
图3 数值模拟与室内试验结果对比图Fig.3 Comparison of numerical simulation and laboratory test results

通过“试错法”标定后的数值模型细观参数见表1。进一步对比数值模拟与室内物理试验结果的峰值应力和弹性模量数值，物理试验结果中峰值应力和弹性模量分别为47.35和0.845 GPa；数值模拟结果中峰值应力和弹性模量分别为45.26 和0.851 GPa。可以发现峰值应力的相对误差＜ 4.5%，弹性模量的相对误差＜ 1%，数值结果吻合度良好，表示该数值模型能够较为真实模拟实际中的充填节理岩石，同时也验证了本文数值模型和细观参数选取的正确性和可靠性。

表1 充填节理岩石数值模型的细观参数表Table 1 Mesoscopic parameter table of numerical model of filled jointed rock

为更好展示单轴压缩过程中微裂纹的发育情况，每间隔10 000 时步（step）记录数值模型在单轴压缩过程中的微裂纹扩展情况（图4）。由图4 可以看出，在时步为20 000 时充填节理层出现首个微裂纹；之后微裂纹不断产生并且多出现于充填节理层的外侧区域；随着时步的增加，充填节理层的微裂纹不断向中部区域扩展，同时还可以看出充填节理层外侧颗粒被挤压移位并发生“逃逸”现象。随着压缩过程的持续进行，充填节理层遍布微裂纹且两侧岩石开始出现微裂纹，两侧岩石的微裂纹不断扩展和汇聚形成肉眼可见的裂缝，继而裂缝不断沿径向发展，最终形成贯通裂缝导致充填节理岩石发生破坏。这与室内试验观察结果一致（图5）。由图5 可以看出，首先是充填节理层被压缩，充填节理层出现一些细小裂纹并且充填节理边缘部位向外隆起并伴有碎屑脱落。随着荷载的施加，充填节理层裂纹不断发展并且充填节理层达到压密状态，两侧岩石开始被压缩并出现微小裂纹。持续加载后两侧岩石裂纹将继续扩展、贯通，最终导致充填节理岩石失稳破坏。通过比对单轴压缩过程中数值模型和室内物理试样的破坏全过程可以看出PFC2D程序可以准确地模拟充填节理岩石的破坏过程，进一步验证了颗粒流数值模拟的可行性。

图4 单轴压缩全过程数值模型的裂纹发育情况Fig.4 Crack development in numerical model of uniaxial compression process

图5 单轴压缩全过程充填节理岩石试样破坏情况Fig.5 Failure of filled jointed rock in the whole process of uniaxial compression

2 结果分析

2.1 不同节理倾角

对不同充填节理倾角（0°、15°、30°、45°、60°、75°和90°）下数值模型进行单轴压缩数值模拟，如图6 为单轴压缩过程的应力-应变曲线。从图6中可以看出，不同节理倾角的充填节理岩石对应的应力-应变曲线差异很大，随着节理倾角的增大，应力-应变曲线先出现下移的趋势，其中节理倾角为30°时应力-应变曲线处于最下方，随着节理倾角的持续增大，应力-应变曲线又逐渐向上方移动，节理倾角为90°时应力-应变曲线处于最上方。进一步分析峰值应力、弹性模量与节理倾角的关系，如图7为不同节理倾角下峰值应力和弹性模量变化曲线。可以发现峰值应力的变化规律呈现出明显的U 型分布，弹性模量的变化规律呈现出近似的U型分布，以往文献研究（陈新等，2011；邓华锋等，2019）中在不同节理倾角下非充填的单节理或多节理岩石峰值应力和弹性模同样也呈现出U 型分布特征，表明充填节理的研究结果与非充填节理岩石较为一致。

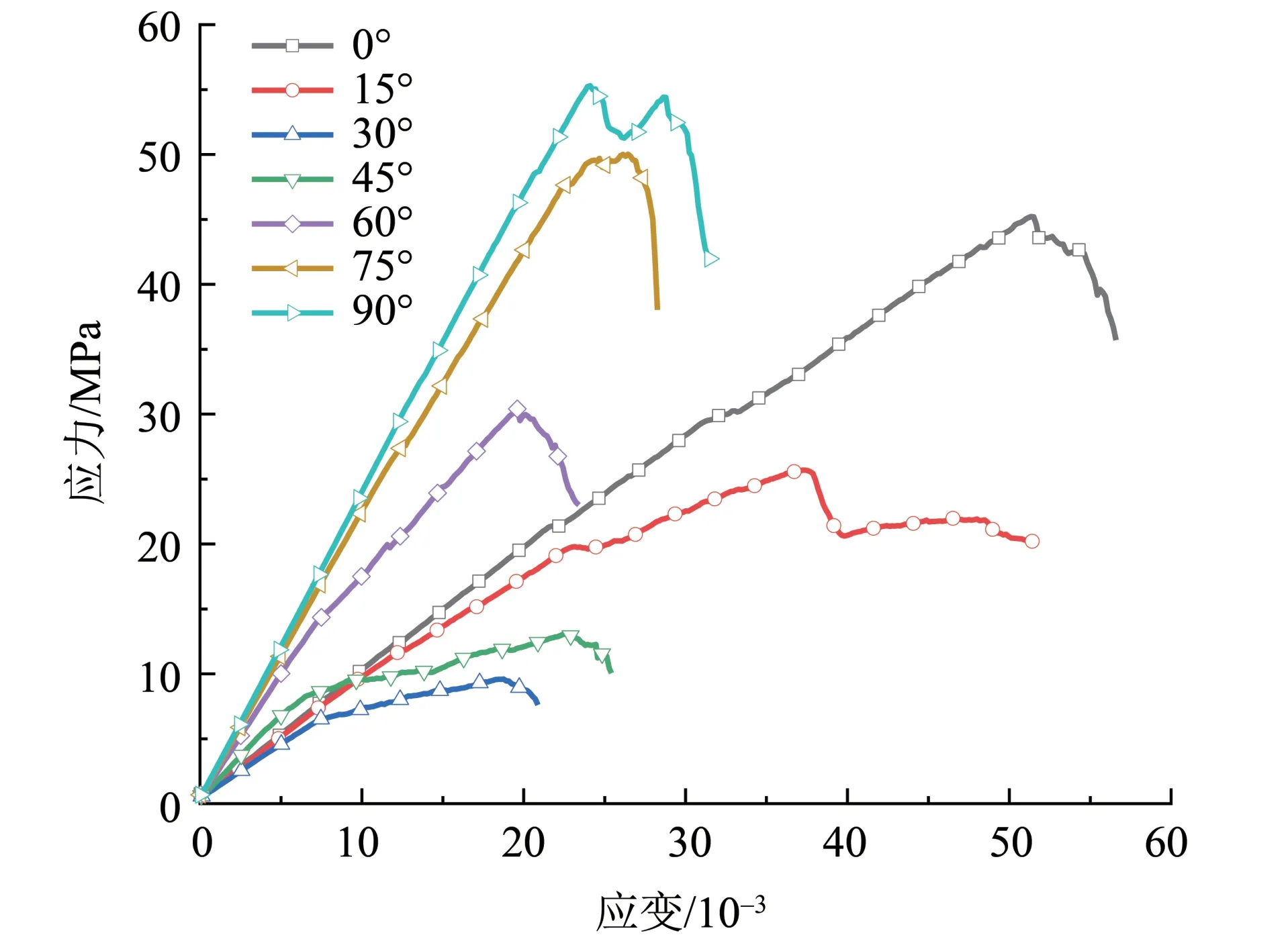
图6 不同节理倾角下数值模型的应力-应变曲线Fig.6 Stress-strain curves of numerical models under different joint angles

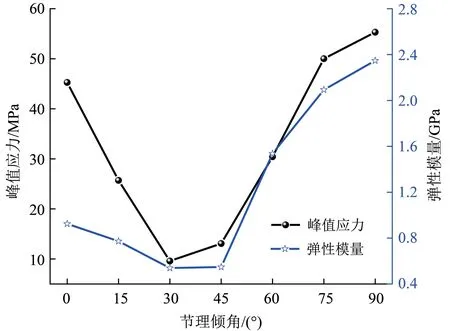
图7 不同节理倾角下峰值应力和弹性模量变化曲线Fig.7 Curve of peak stress and elastic modulus under different joint angles

此外，从图7 中还可以看出，节理倾角为90°时，峰值应力和弹性模量最高；节理倾角为30°时，峰值应力和弹性模量最低。节理倾角90°时峰值应力和弹性模量分别为55.3 和2.348 GPa，较0°倾角时分别提高了22.18%和153.84%。节理倾角为30°时峰值应力和弹性模量分别为9.59 和0.539 GPa，较0°倾角时分别下降了78.81%和41.73%。

为研究压缩过程中不同节理倾角下微裂纹的发育情况，提取不同节理倾角下微裂纹数量随应变的变化曲线，如图8所示。结果发现不同节理倾角下微裂纹的变化曲线差异较大。当充填节理处于水平位置时数值模型的微裂纹发育主要呈现出前期增长较快、中期增长缓慢、后期迅速增长的3阶段特点。对照图4 对所呈现的微裂纹3 阶段发育特点的分析如下：前期裂纹增长较快的主要原因是充填节理层强度及模量较低，在压力作用下更易产生裂纹且低强度材料中裂纹扩展较快；中期裂纹增长缓慢的主要原因是充填节理层裂纹不再增加，裂纹产生位置逐步转移至两侧岩石层；后期迅速增长的主要原因是两侧岩石层裂纹在压力作用下不断汇聚和扩展，充填节理试样趋于失稳破坏。

从图8中还可以发现当节理倾角改变时微裂纹发育情况也发生改变，当节理倾角为15°时数值模型的微裂纹发育还近似呈现为3阶段特点，但可以看出微裂纹变化曲线出现明显向左偏移现象，表明同一应变下节理倾角为15°数值模型的微裂纹数量更多；当节理倾角增加至30°时数值模型的微裂纹发育不再呈现典型的3阶段特点，而是呈现出前期增长缓慢、后期增长迅速的2阶段特点，随着节理倾角的持续增加，节理倾角为45°、60°和75°时数值模型的微裂纹发育又近似呈现出3 个阶段特点，但微裂纹发育曲线历程明显缩短，而当节理倾角为90°时，微裂纹发育情况与节理倾角为30°时类似，上述现象说明节理倾角改变会严重影响充填节理岩石裂纹的发育。进一步提取最终破坏时不同节理倾角下微裂纹总数量，如图9所示。从图9中可知充填节理岩石在不同节理倾角下最终破坏时的总裂纹数分别为1 030、990、839、774、585、865和901，可知随着节理倾角的变化，最终破坏时总裂纹数呈现出先减小后增大的变化趋势。

图9 不同节理倾角下最终破坏时微裂纹总数量Fig.9 Total number of microcracks at final failure under different joint angles

引入起裂应力进行深入分析，将单轴压缩过程中微裂纹数为峰值应力时微裂纹数的1%对应的轴向应力定义为起裂应力（Potyondy et al.，2004），如图10 所示。进一步可以得到不同节理倾角下起裂应力的变化情况，如图11 所示。从图11 中可以看出，当节理倾角不同时，充填节理岩石数值模型的起裂应力分别为8.33、7.52、4.06、5.46、10.65、17.24 和30.61 MPa。充填节理岩石数值模型的起裂应力随节理倾角的增大出现先减小后增大的趋势，也呈现出近似U 型分布的特点，其中起裂应力最小时对应的节理倾角为30°，起裂应力最大时对应的节理倾角为90°，也就表明当节理倾角为30°时充填节理岩石最容易率先产生裂纹，而节理倾角为90°时充填节理岩石最不易产生裂纹。

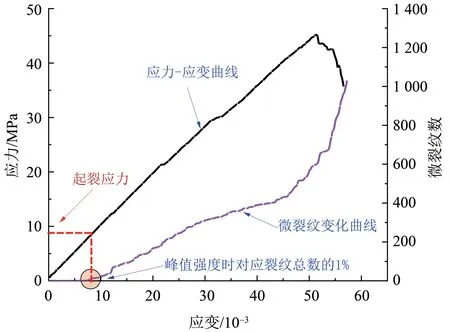
图10 起裂应力示意图Fig.10 Diagram of initiation stress

图11 不同节理倾角下起裂应力变化曲线Fig.11 Fracture initiation stress curve under different joint angles

进一步通过图12 观察不同节理倾角下充填节理岩石最终破坏形态可以看出，节理倾角会显著影响充填节理岩石的破坏形态。当充填节理处于水平位置时，数值模型最终破坏形态表现为充填节理层发生很大的竖向压缩并且两侧岩石出现贯通裂缝；当节理倾角为15°时，充填节理层产生了较大的竖向压缩且数值模型的上侧岩石出现滑移现象，岩石层微裂纹很少，微裂纹基本集中在充填节理层；随着节理倾角的增大，充填节理层压缩量减小，当节理倾角为60°时，充填节理岩石总裂纹数明显减小，充填节理层与岩石层出现一定程度的脱离，岩石层出现一条贯通大裂缝最终导致试样破坏；随着节理倾角的继续增大，岩石层的微裂纹数量持续增多，当节理倾角为90°时，可以看出岩石层的破坏最为严重，由上文所述可知节理倾角为90°时数值模型的峰值应力和起裂应力最大，由此可以推断出当节理倾角较小时，竖向压力作用主要由充填节理层和两侧岩石层共同承担，而当节理倾角较大时，竖向压力作用主要由两侧岩石层承担。

图12 不同节理倾角下充填节理岩石最终破坏形态Fig.12 Final failure pattern of filled jointed rock under different joint angles

2.2 不同充填节理厚度

图13 为5 种不同充填厚度（2.0、3.5、5.0、6.5和8.0 mm）的充填节理岩石单轴压缩的应力-应变曲线。可以看出，应力-应变曲线变化趋势较有规律，随着充填节理厚度的增加，充填节理岩石的应力-应变曲线逐渐向下方移动，其变化趋势与试验结果一致（Chai et al.，2020）。充填节理厚度分别为6.5 和8.0 mm 时应力-应变曲线峰前出现波动现象，这是由于充填节理厚度较大时在压缩过程中充填层颗粒会发生错动和向外挤压情况。充填厚度改变时充填节理岩石的峰值应力和弹性模量的变化规律如图14所示。

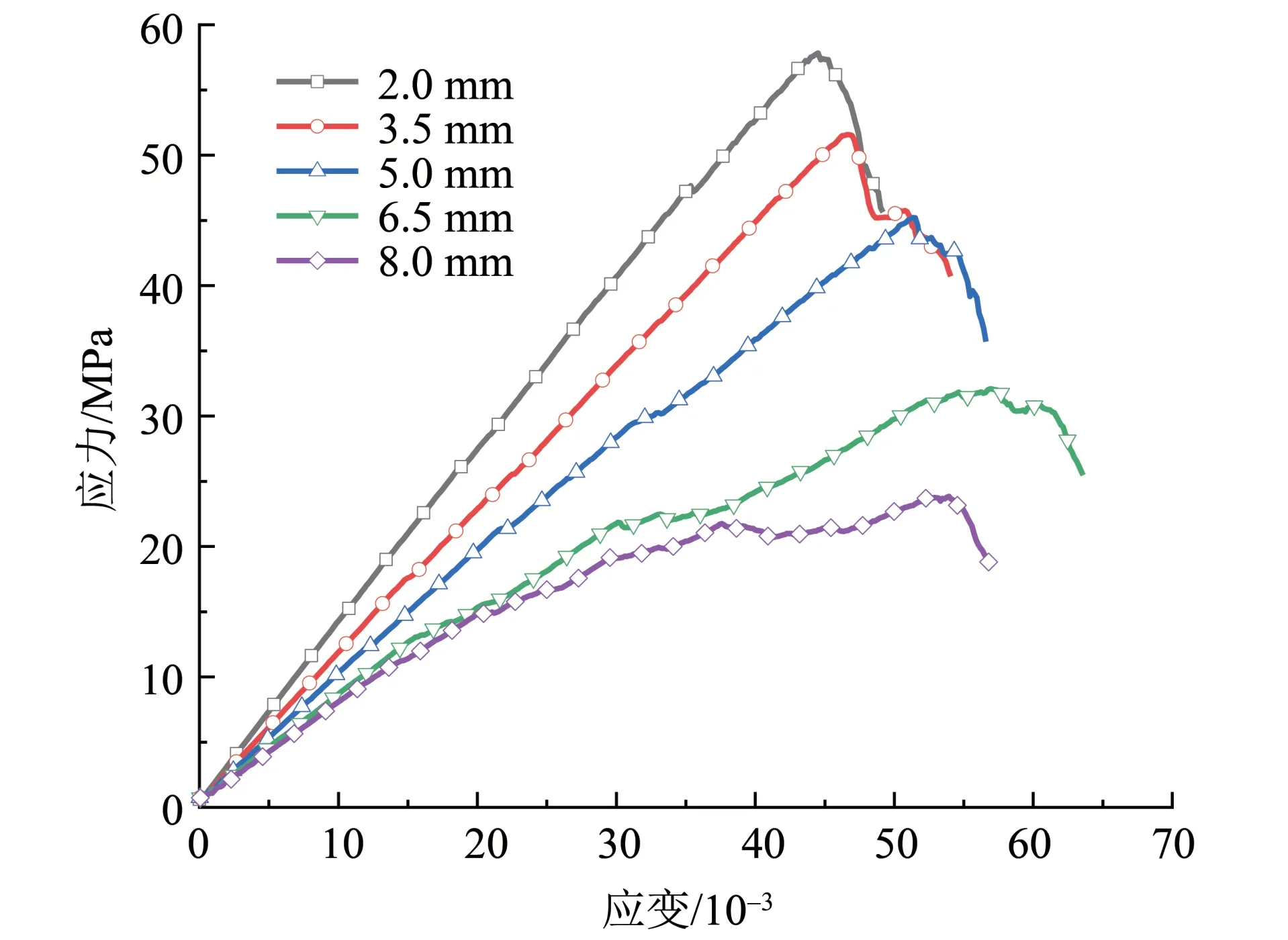
图13 不同充填厚度下数值模型的应力-应变曲线Fig.13 Stress-strain curves of numerical models under different filling thicknesses

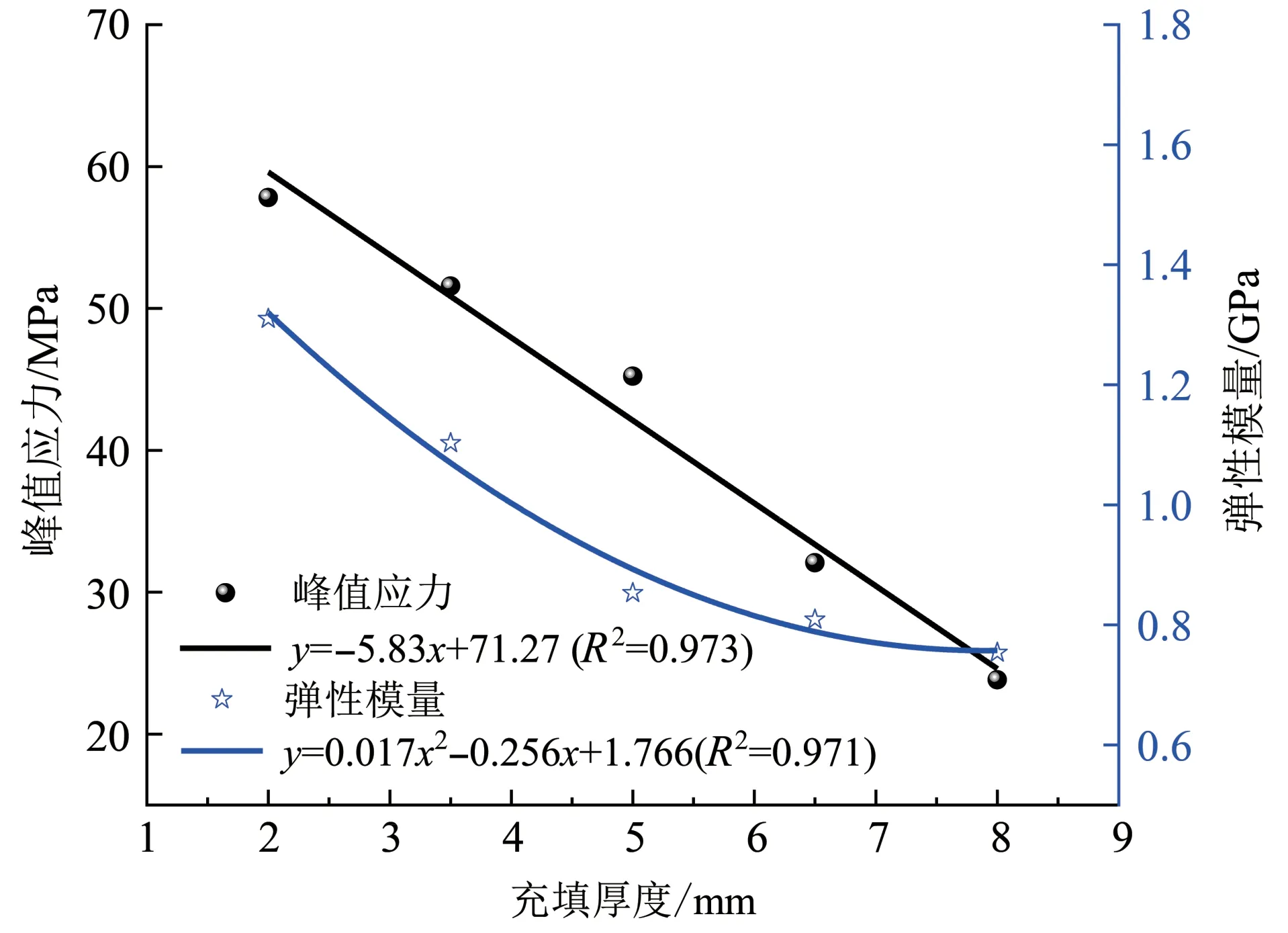
图14 不同充填厚度下峰值应力和弹性模量变化曲线Fig.14 Curve of peak stress and elastic modulus under different filling thickness

从图14 可知当充填节理厚度不断增加时，数值模型的峰值应力分别为57.82、 51.58、45.26、32.08 和23.83 MPa，弹性模量分别为1.31、1.103、0.851、0.809和0.754 GPa。充填厚度增加至3.5mm时峰值应力和弹性模量分别降低了10.79% 和15.8%；充填厚度增加至5.0 mm时峰值应力和弹性模量分别降低了21.72%和35.04%；充填厚度增加至6.5 mm 时峰值应力和弹性模量分别降低了44.52%和38.24%；充填厚度增加至8.0 mm 时峰值应力和弹性模量分别降低了58.79%和42.44%。可以发现峰值应力和弹性模量随充填厚度的增加而逐渐降低，并且弹性模量降低速度逐渐变缓，进一步通过拟合发现峰值应力的降低趋势符合线性函数分布，而弹性模量的降低趋势符合多项式函数分布，相关系数均大于0.97，说明一致性良好。

深入分析不同充填厚度情况下微裂纹的发育情况，如图15 所示。从图15 中可以看出不同厚度充填节理岩石数值模型微裂纹的发育过程也呈现典型的3 阶段特点，但随着充填节理厚度的增加，微裂纹数随应变的变化曲线逐渐向上侧移动，从微裂纹发育的第2阶段可以明显看出微裂纹数量从高到低依次为8.0、6.5、5.0、3.5、2.0 mm，且充填节理厚度较大时第2 阶段的微裂纹数量明显增多。从图16 可知当充填节理厚度不断增加时，最终破坏时数值模型的总裂纹数分别为744、903、1 030、1 251 和1 399，最终破坏时数值模型的总裂纹数随着充填节理厚度的增加而不断增加，通过拟合发现总裂纹数的增长趋势符合线性函数分布，且一致性良好。进一步计算不同充填厚度下充填节理岩石的起裂应力数值，结果发现随着充填节理厚度的增加时起裂应力分别为10.12、7.52、8.19、6.02 和6.32 MPa，可以看出不同厚度充填节理岩石的起裂应力基本处于6～10 MPa 范围之内，说明充填节理厚度改变对起裂应力影响不大。

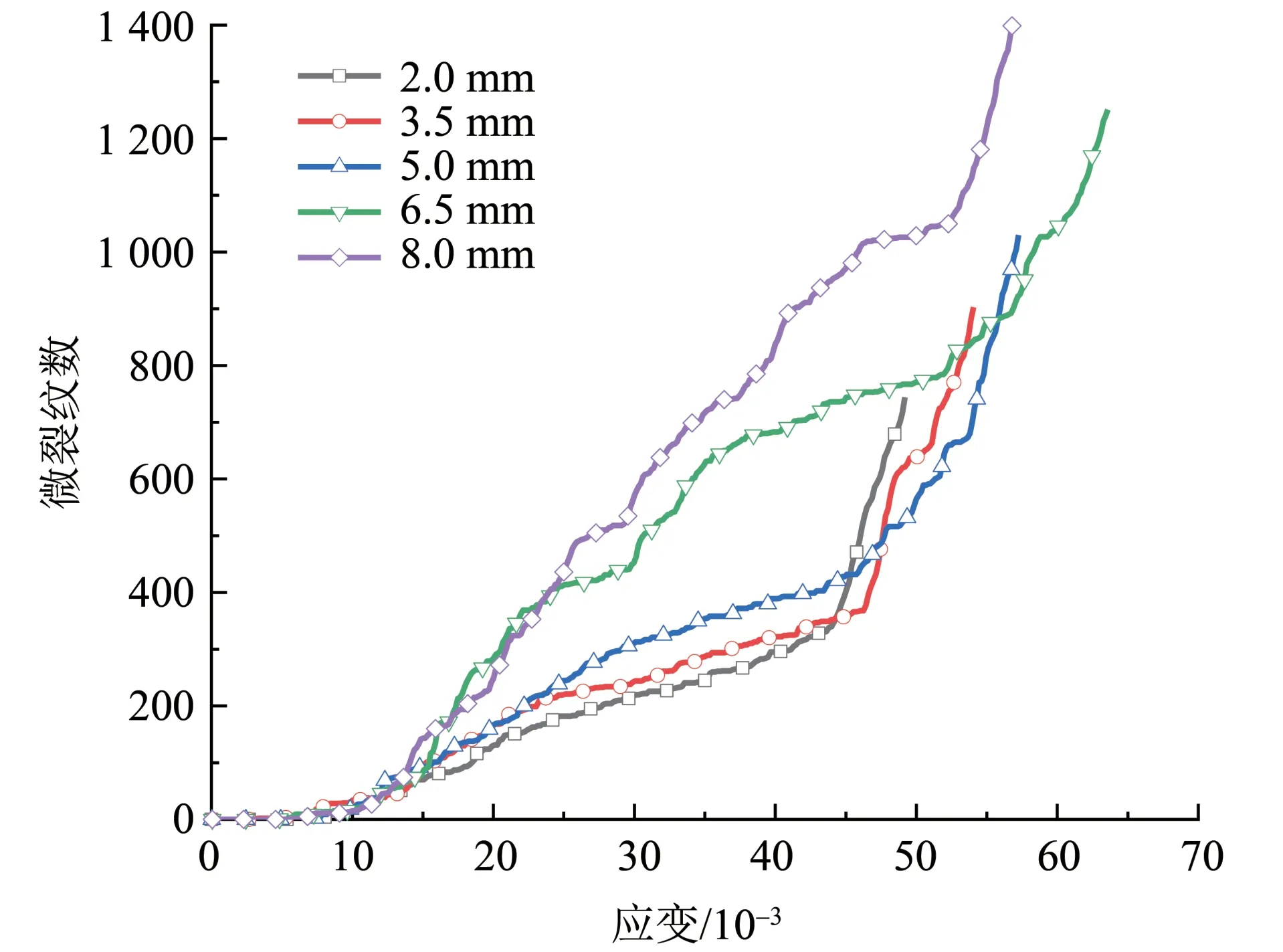
图15 不同充填厚度下微裂纹数量变化曲线Fig.15 Variation curve of the number of microcracks under different filling thicknesses

图16 不同充填厚度下最终破坏时微裂纹总数量Fig.16 Total number of microcracks at final failure under different filling thicknesses

如图17 为不同厚度充填节理岩石数值模型的最终破坏形态。可以发现随着充填节理厚度的增加，最终破坏时充填节理层颗粒受挤压向两侧外溢、脱落情况严重，同时还发现两侧岩石层的微裂纹较少，微裂纹多集中于充填节理层，说明压缩过程中充填节理层受损程度更严重，此外还可以看出不同厚度充填节理岩石数值模型最终破坏模式为张拉破坏，可以表明改变充填节理厚度对充填节理岩石压缩破坏模式并无影响。

图17 不同充填厚度下充填节理岩石最终破坏形态Fig.17 Final failure pattern of filled jointed rock under different filling thickness

2.3 一组平行分布充填节理

实际自然界岩体内部中节理是成组出现的，为进一步对比1组节理与单个节理情况下力学及变形特性的差异性，在数值模型建立过程中设置1组平行分布的充填节理（3 条节理），并且控制充填节理的总厚度5 mm 不变，其中充填节理层和岩石层的细观参数与上文一致。以此来研究含1组平行充填节理情况下节理岩石的力学及变形特性，如图18为不同节理倾角下含1组平行充填节理数值模型的应力-应变曲线。进一步可以得到含1 组平行充填节理的岩石试样在不同节理倾角下的峰值应力和弹性模量，如图19所示。

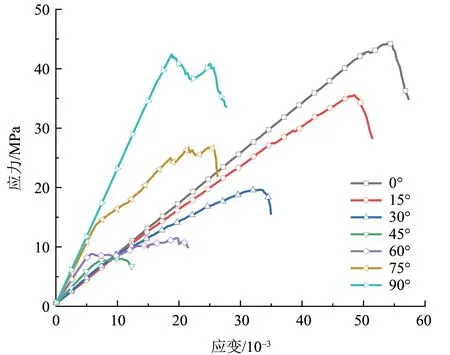
图18 不同节理倾角下含1组平行充填节理的应力-应变曲线Fig.18 Stress-strain curves of a group of parallel filled joint under different joint angles

图19 不同节理倾角下含1组平行充填节理峰值应力和弹性模量变化曲线Fig.19 Curves of peak stress and elastic modulus of a group of parallel filled joint under different joint angles

由图18 中可以看出，含1 组平行充填节理的岩石试样的应力-应变曲线随着节理倾角的增大出现先向左下方移动后向左上方移动的现象，与含单个充填节理的岩石应力-应变曲线随节理倾角的变化趋势相同。不同的是，含1组平行充填节理的岩石试样在节理倾角为45°时的应力-应变曲线处于最下方。由图19 可以发现，随着节理倾角的增加，峰值应力和弹性模量均出现先减小后增大的趋势。相比于含单个充填节理的岩石，含1组平行充填节理的岩石在节理倾角为0°时峰值应力差异较小；节理倾角为15°和30°时峰值应力分别提高了38.3%和104.9%；节理倾角为45°、60°、75°和90°时峰值应力分别降低了38.4%、62.3%、46.5%和23.3%；可以发现当节理倾角小于45°时含1 组平行充填节理的岩石峰值应力较高，而节理倾角大于45°时含单个充填节理的岩石峰值应力较高，其主要原因是当节理倾角较小时，如图20 所示可以看出含单个充填节理的岩石数值模型颗粒间接触力分布不均匀，充填节理层两侧位置处的接触力较大，而含1组平行充填节理的岩石数值模型颗粒间接触力分布较为均匀。所以相比于充填节理集中布设在岩石中部，充填节理分散分布于岩石试样内部可以使得压力作用下充填节理岩石整体受力更为均匀，可以减小颗粒间接触断裂的可能性。而当节理倾角较大时，由于多条充填节理的存在，在压缩过程中充填层与岩石层易发生分离脱落现象，从而降低了充填节理岩石整体的强度及稳定性。

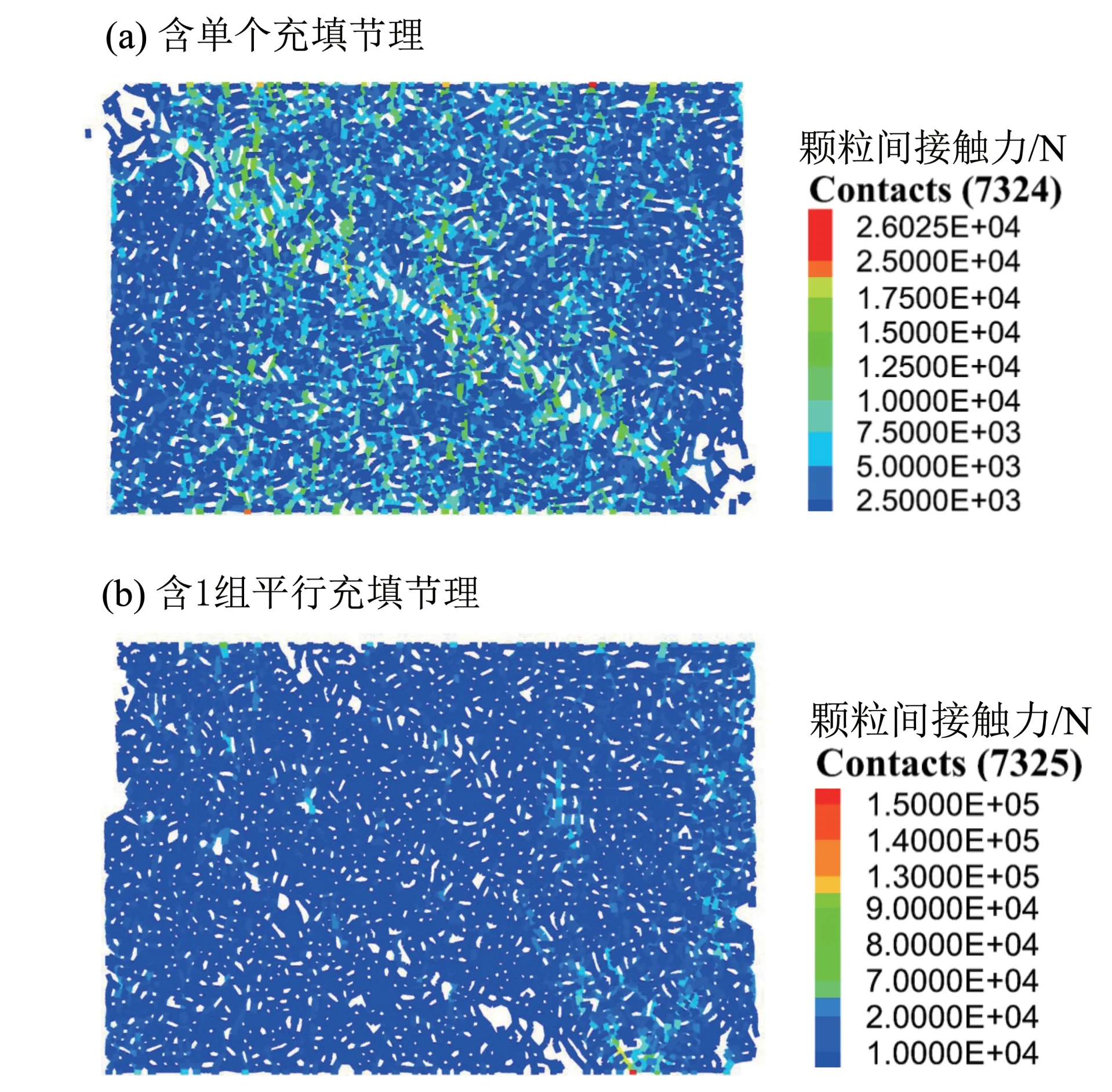
图20 充填节理岩石数值模型颗粒间接触力分布图Fig.20 Distribution of contact forces between particles in numerical model of filled jointed rock

进一步分析不同节理倾角下含1组平行充填节理的微裂纹变化曲线，如图21 所示。可以看出节理倾角为0°时微裂纹变化曲线同样呈现出典型的3阶段特点。随着节理倾角的增加，微裂纹发育的变化情况与含单个充填节理的岩石变化情况类似。图22 为不同节理倾角下含1 组平行充填节理最终破坏时微裂纹总数量，可以看出随着节理倾角的增加，最终破坏时总裂纹数也呈现出先减小后增大的趋势，通过对比含单个节理的岩石数值模型的总裂纹数发现两者相差较小，说明充填节理数对单轴压缩过程中微裂纹情况影响较小。

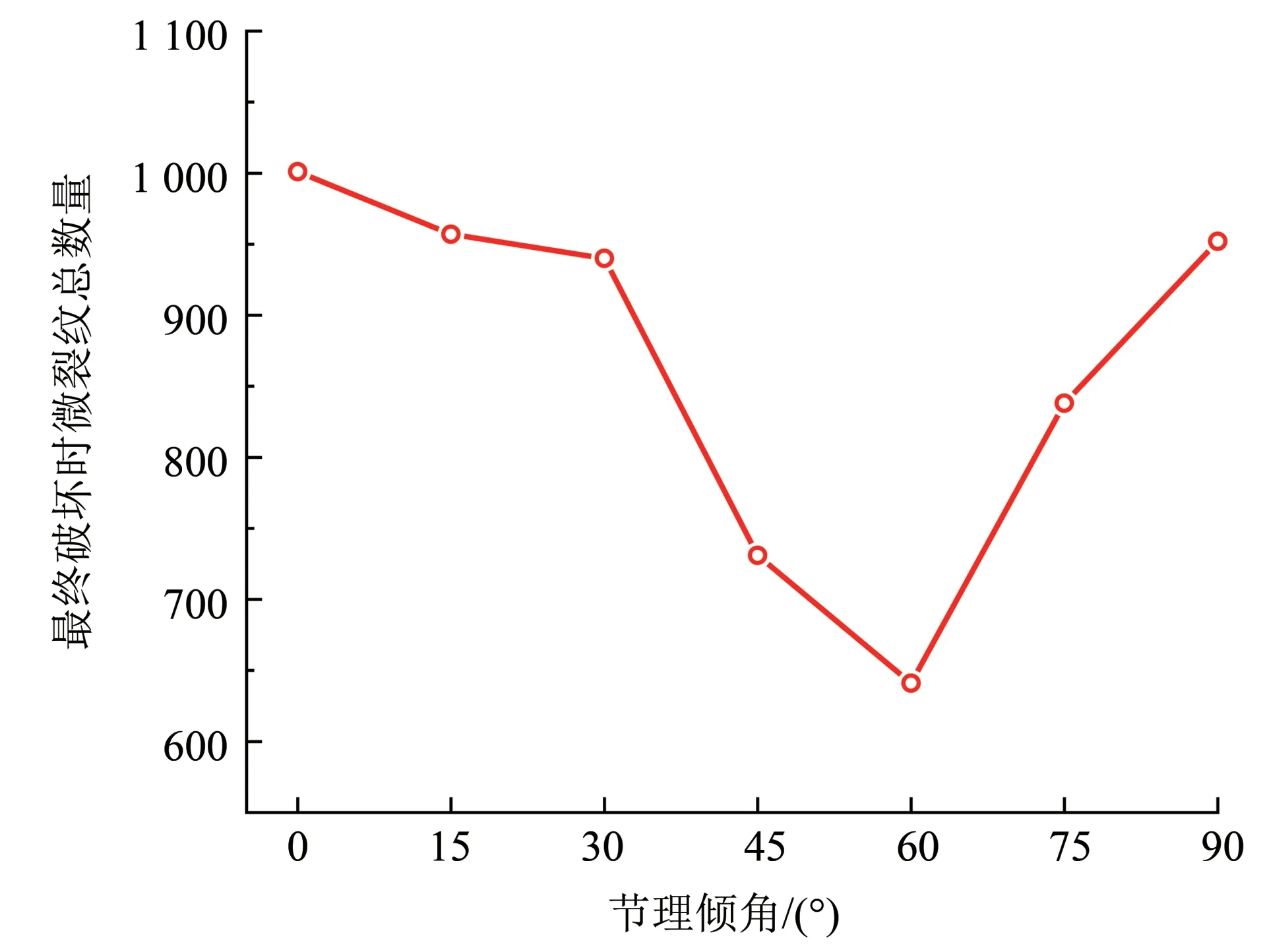
图22 不同节理倾角下含1组平行充填节理最终破坏时微裂纹总数量Fig.22 The total number of microcracks in a group of parallel filling joints under different joint angles

图23 为不同节理倾角下含1 组平行充填节理的岩石最终破坏形态。由图23 可以看出，不同节理倾角下数值模型最终破坏形态差异较大，节理倾角为0°和15°时，充填节理层之间的岩石层均出现了贯通裂缝，节理倾角为30°时最终破坏形态完整性较好，当节理倾角大于45°后充填节理层出现分离剥落现象，尤其当节理倾角为75°时分离剥落现象最为严重，充填节理层均发生了明显的滑移破坏，可知当节理倾角较大且岩石内部含有多条充填节理时整体稳定性较差、破坏程度严重。

图23 不同节理倾角下含1组平行充填节理最终破坏形态Fig.23 Final failure form of a group of parallel filling joints under different joint angles

3 结 论

本文利用PFC2D程序构建了充填节理岩石数值模型，结合室内静态单轴压缩试验结果验证了细观参数选取的可靠性以及颗粒流模拟的可行性，分析了不同节理倾角、多条节理数以及不同节理厚度情况下充填节理岩石的力学参数变化规律、微裂纹扩展和破坏形态情况，主要结论如下：

1）随着充填节理倾角的改变，峰值应力和弹性模量呈现出U 型分布，最终破坏时的总裂纹数和起裂应力呈现出先减小后增大的变化趋势，此外改变充填节理倾角会严重影响充填节理岩石裂纹的发育状况和最终破坏形态。

2）充填节理岩石的峰值应力和弹性模量随充填厚度的增加而逐渐降低，且弹性模量降低速度逐渐变缓，而最终破坏时的总裂纹数随着充填厚度的增加而不断增加，进一步拟合发现峰值应力和总裂纹数的变化规律符合线性函数分布，弹性模量的变化规律符合多项式函数分布。

3）不同充填厚度的节理岩石微裂纹的发育过程均呈现典型的3阶段特点，即微裂纹前期增长较快、中期增长缓慢、后期迅速增长；但充填节理厚度改变对起裂应力和破坏模式影响不大。

4）岩石内部存在1组平行充填节理时，随着节理倾角的增加，峰值应力和弹性模量均出现先减小后增大的趋势，最终破坏时总裂纹数也呈现出先减小后增大的趋势。但当节理倾角较大会发生明显的滑移破坏，充填节理岩石整体稳定性较差、破坏程度严重。

本文进行的数值模拟研究是基于二维颗粒流程序，二维颗粒流数值模拟未能反映节理面的空间形态特性和三维应力状态等真实情况，存在一定的不足和缺陷，但基于二维颗粒流程序的数值模拟一定程度上可以反映实际规律。此外，实际工程中充填节理分布复杂且充填节理材料差异明显，本文研究中暂未考虑相关因素，仅是对节理倾角、充填厚度等因素展开分析，研究结果在一定程度上可为后续分析复杂分布节理岩体稳定性提供参考。