基于加速度信号分解和正则化的宽频位移重构方法*

陈信君， 吕中荣， 汪利

中山大学航空航天学院，广东 深圳 518107

结构系统的动力响应测量在地震分析（Boore et al.，2005；Hsieh et al.，2011；Tomita et al.，2015）、结构振动试验与控制（Ma et al.，2011）、动力系统识别与结构健康监测（Park et al.，2013；Park et al.，2015； Ma et al.，2023）、结构损伤评估（杨达豪等，2021；谭颖轩等，2022）等工程领域有着广泛的需求。而在动力响应中，动力位移时程可以反映结构的刚度和内部受力特征，是描述结构动态特性最重要的测量指标之一。

虽然位移信息非常有用，但其在实践中的测量往往较为困难（Xu et al.，2017）。一般而言，结构的位移响应可以通过以下两种方式获得：① 接触式传感器；② 非接触式传感器。线性可变差动变压器（LVDT）是最常用的接触式设备之一，需要在结构和固定参考点之间建立连接。对于大型结构，比如大跨度桥梁、高层建筑等，参考点几乎无法布置，导致常规LVDT无法直接测量位移信息。非接触式方法包括激光多普勒振动计、全站仪、GPS定位仪等，虽然位移测量方便，但可能存在精度较低问题（Nassif et al.，2005），且成本较高。

与位移测量不同，加速度的测量无需参考点，常见的加速度计精度高、成本低，已被广泛应用于大型结构振动测量。基于高精度的加速度测量，目前已有研究和工程应用考虑从加速度信息中重构位移响应（Sohn et al.，2011）。

理论上，可以通过对加速度信号进行二重积分得到位移响应。但是，直接积分对低频噪声十分敏感，导致出现低频漂移现象（Bardella et al.，2003）。低频漂移会引起严重的信息失真，大大降低位移重构的精度。因此，如何解决加速度积分中的低频漂移受到了研究人员的广泛关注。到目前为止，已经根据加速度信息，发展出了时域积分（Park et al.，2008；陈培永等，2011），数字滤波（李智勇，2009）和频率领域集成（郝春冬等，2021）等位移重构方法。

本文主要提出一种基于有限带宽信号分解和正则化的宽频位移重构新方法。首先，在已有加速度积分中引入Tikhonov正则化（Lee et al.，2010），克服低频漂移问题。正则化方法适合于单一主频（或窄频）的位移重构，难以处理实际工程测试中的宽频加速度信号。为此，进一步提出有限带宽信号分解方法，将宽频加速度信号分解为若干窄频信号，然后，利用正则化方法对每个窄频信号进行高精度的位移重构。最后，还将通过数值和实验算例验证方法的有效性。

1 基于加速度积分与正则化的位移重构

根据加速度a(t)重构位移响应u(t)涉及如下微分边值问题

假设测量得到时间间隔为Δt的离散加速度信号，记ai，ui分别为ti=iΔt时刻的加速度和位移，其中i表示第i个时间步，对式（1）进行二阶差分，忽略高阶误差，可得

或者矩阵向量方程

其中

B表示N×(N+ 2)阶线性代数矩阵。

由于B矩阵是非列满秩的，通过式（3）从加速度得到位移是一个不适定的反问题。

给定初始位移和速度条件，直接求解式（3）可得，位移是加速度的二重积分。但由于存在噪声，即使初始条件是准确的，直接积分所得结果仍然会发生“低频漂移”，即随着时间推移，位移误差越来越大。记测量的加速度为aˉ(t)，真实加速度为a（t），可建立目标函数使以下误差平方函数ΠE取最小值

将其写成离散形式，并考虑式（3），可得

其中

是N阶权量矩阵，||·||2表示向量的2范数。

为了克服不适定性，避免出现低频漂移，采用Tikhonov 正则化方法，为上述最小化问题增加一个罚函数项，可得

其中λ正则化因子，式（5）中的系数1/（2(Δt)3）因不影响结果而被省略。求解式（6）可得

其中I表示单位矩阵。以上求解中，正则化因子λ的取值对位移重构的精度起着关键性的作用。如果λ趋近于0，正则化无法带来稳定效益；反之，如果λ的值很大，方程的解将趋近于0.

通常可以使用L曲线法和交叉验证法确定上述反问题的最佳正则化因子，但它们的计算成本是十分巨大的。基于单自由度自由振动，Lee et al.（2010）提供了一个经验选取法则，将正则化因子作为时间窗口[t1，tN]内点数量的函数来确认最优正则化因子，即

此外，为了进一步降低噪声的影响，所取时间窗长度tN-t1一般取主频周期的3 倍（Lee et al.，2010）。为了减少边界附近位移估计不准确性的影响，使用重叠时间窗技术。重叠时间窗口以时间增量而非时间窗口大小为单位向前移动，位移重构在每个时间窗口中依次进行，但每次只取该时间窗中心的重构位移作为时间窗中点的解。重叠窗的计算示例见图1，它针对每个点的位移重构引入不同的时间窗。比如，假设时间窗长度为N=2k+1，为了重构tl时刻的位移，需要在时间窗[tl-k，tl+k]内求解式（7），并取ul作为tl点的重构位移解，而舍弃其他点的结果。

重叠时间窗和正则化方法确实能准确重构低频主导的位移响应。但实际工程中，结构可能出现宽频响应，即其包含多阶频率信息，且多个频率分布十分广泛。此时，该方法难以得到满意的位移恢复结果。接下来，将在已有方法的基础上，进一步提出宽频加速度信号的有限带宽分解方法，解决宽频位移重构问题。

2 面向宽频位移重构的有限带宽信号分解

基于加速度积分与正则化的位移重构方法克服了低频漂移现象，但其时间窗长度的选取与结构的主频周期有关，理论上适用于处理低频主导或窄频加速度信号。对于宽频加速度信号，这里拟引入有限带宽信号分解，将宽频加速度信号分解为若干窄频信号，进而使用已有方法对每个窄频信号进行高精度位移重构，最终实现宽频位移的准确重构。

宽频信号加速度a(t)包含多个主频峰值段，可按照频率分布特征，分解为若干窄频（或有限带宽）的信号

其中a1(t)，a2(t)，…，am(t)为有限带宽信号，它们的频率被限制在不同的频域范围内。具体而言，引入m- 1 个频率分割点0 ＜σ1＜… ＜σm-1＜∞，将原始信号分解成m个有限带宽信号，第一个信号a1(t) 为限定在频域|ω| ≤σ1上的信号，第k个信号ak(t)限制在频域σk-1＜|ω|≤σk，k=2，…，m- 1 上，第m个信号am(t)限制在频域|ω|＞σm上。a1(t)，a2(t)，…，am(t)在频域上的表现形式如图2所示。

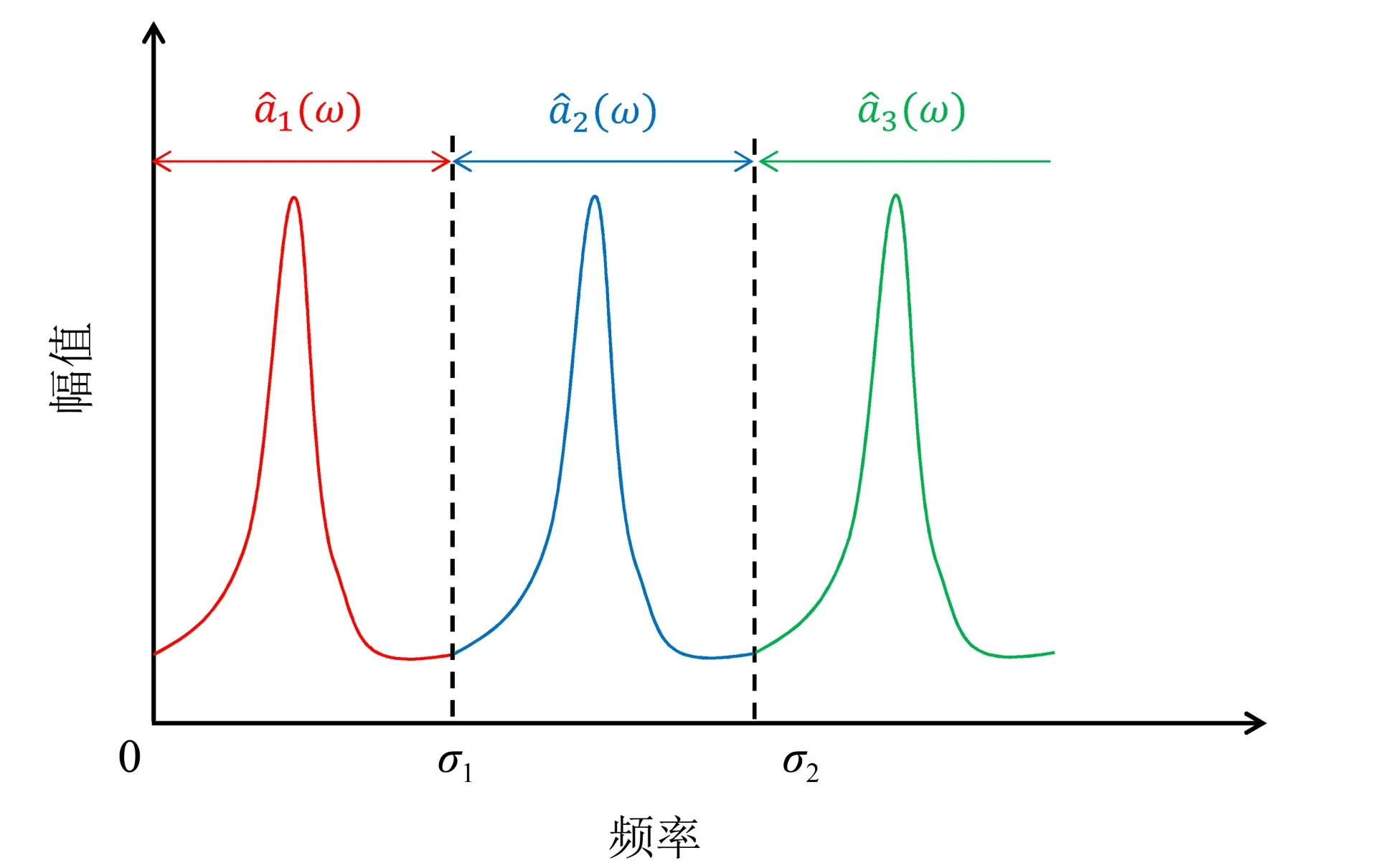
图2 频域上的有限带宽信号分解示意图Fig.2 Schematic diagram of finite bandwidth signal decomposition in frequency domain

如何快速实现有限带宽信号分解是一个关键问题。记â(ω)表示任意时域信号a(t)的频域上的Fourier变换。此时，理论上有

其中T表示整个时间信号的长度。式（10）的关键在于计算卷积

其离散表达为

式（11）为循环卷积式，直接根据该式进行计算效率不高。这里使用一种快速的循环卷积算法，能极大地提高计算效率。

循环卷积算法（Brandt，2019）基于Fourier 变换和卷积原理，通过对每个序列进行快速Fourier变换、逐点相乘，然后执行逆Fourier 变换，从而得到两个有限长度序列的循环卷积。该方法能将计算时间复杂度从O()降低到O(NTlogNT)，具体计算公式如下

其中

均为长度为2NT的向量，FFT和IFFT分别表示快速Fourier变换和逆变换算法，x的前NT项表示为

结合循环卷积算法和有限带宽信号分解式（10），可快速得到分解后的有限带宽信号ak(t)，k= 1，2，…，m.由于每个信号ak(t)为窄频或只有单个主频率，可应用第1节的正则化方法准确重构得到相应位移响应uk(t)，最后，根据信号叠加原则，可得重构的宽频位移响应为

综上所述，本文所提宽频位移重构的具体流程如图3所示。

图3 宽频位移重构方法分析流程Fig.3 Analysis flow of broadband displacement reconstruction method

3 数值算例

3.1 加速度信号验证

为了验证所提出方法的可行性，构造一个具有两个频率分量的位移信号，两个频率成分分别为和，即

对上述信号进行二次微分，即得到加速度信号。对加速度信号按200 Hz 频率采样，可得到加速度数据。为了尽可能真实地模拟实测的加速度信号，对模拟信号施加高斯白噪声

其中a͂(t)，a(t)分别表示施加噪声和未施加噪声的加速度信号，nr表示噪声水平，ϵ为满足标准高斯分布的随机数，σa为原始信号的标准差。

将执行两种不同的位移重构方案并将位移重构结果进行对比：方案一使用基于加速度积分与正则化的位移重构方法（见第1节），方案二则使用本文提出的基于有限带宽信号分解的位移重构新方法（见第2节）。

首先，分别考虑无噪声和nr=10%高斯噪声的情形，位移重构结果如图4 和图5 所示。可以看出，方案一给出的位移重构结果在一定程度上也能接近真实位移，但方案二的位移重构误差明显更小。尤其在信号两端，方案一存在较大的扰动，而方案二仍能给出准确的位移重构结果。其次，为了量化两种方法的精度，引入重构位移与准确位移的相对误差RE和互相关系数COR分别为

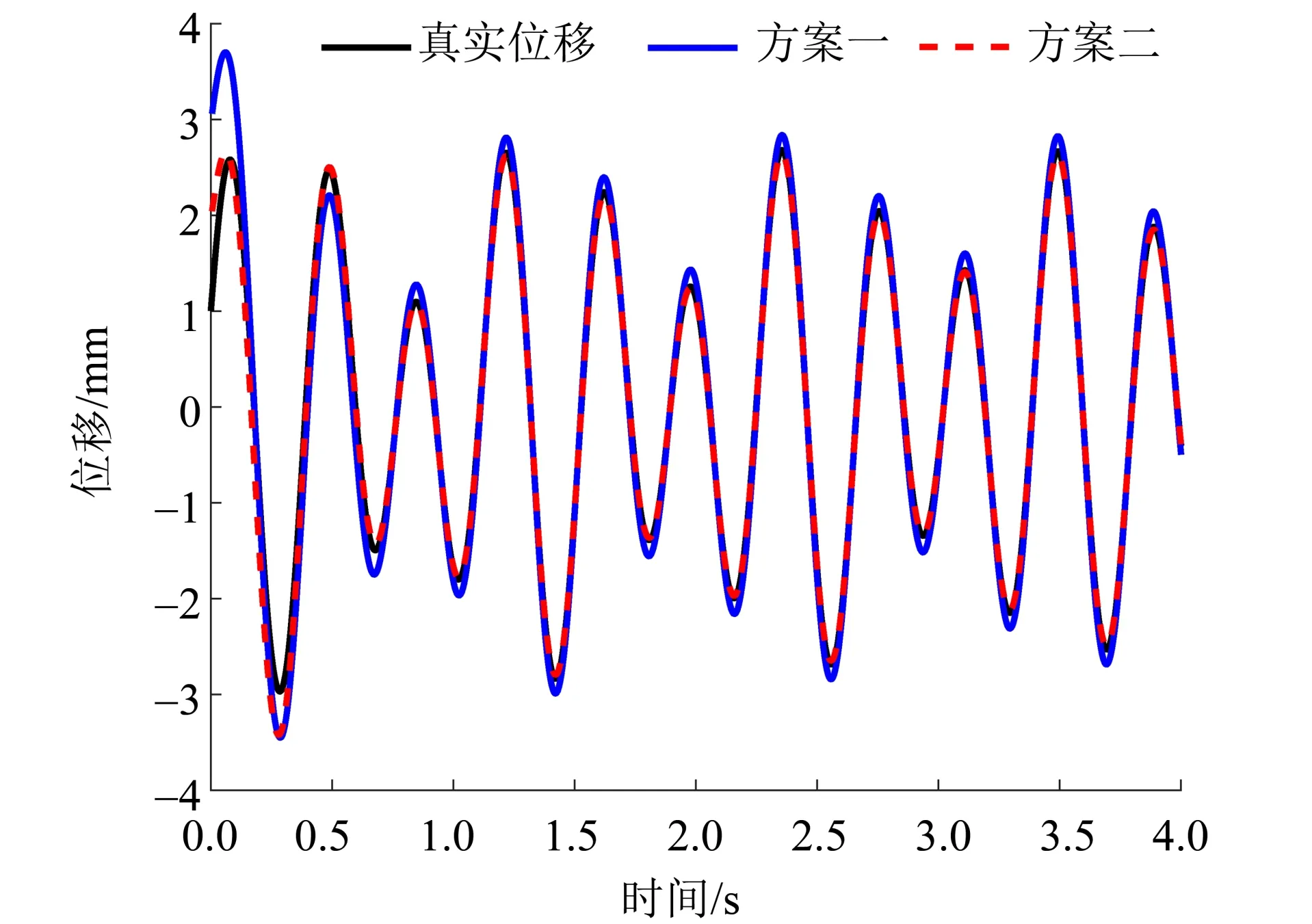
图4 无噪声时两种位移重构方案的结果图Fig.4 Estimated displacement by scheme I and scheme Ⅱ for acceleration signal without noise

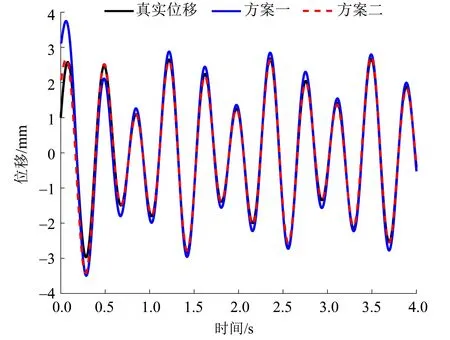
图5 nr = 10%的噪声下两种位移重构方案的结果图Fig.5 Estimated displacement by scheme I and scheme Ⅱfor acceleration signal with nr = 10% noise

其中uE表示离散时间点上的重构位移，uR为真实位移。显然，RE 越小，COR 越接近1，位移重构精度越高。根据式（15），可以定量计算方案一和方案二的相对误差和互相关系数，结果见表1。结果指出，方案二的相对误差小于方案一相对误差的一半，且互相关系数也越接近1。显然，有限带宽信号分解确实能够显著提高宽频位移重构的精度。

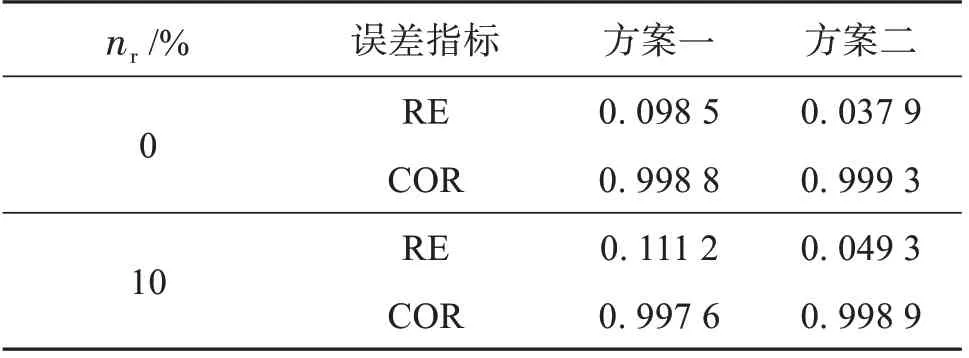
表1 不同噪声下两种位移重构方案的误差Table 1 Errors of scheme I and scheme Ⅱunder different noises

上述结果验证了基于有限带宽信号分解的位移重构方法能准确重构宽频位移，但该结构频率分布较为稀疏。为了进一步讨论中高阻尼、近频下该方法的有效性，考虑重构如下位移信号

其阻尼比接近10%，加速度数据通过位移微分和施加5%噪声得到。位移重构过程中，该信号的近频成分0.98 rad/s 和1 rad/s 限制在一个频域范围，频率成分rad/s 限制在另一个频域范围，通过分割频率σ1= 1.8 rad/s将信号分解成两个有限带宽信号。基于有限带宽信号分解的位移重构效果如图6所示，可以看到，得到的位移与真实位移十分吻合，且识别误差RE = 0.143 4，COR =0.989 8.显然，本文方法也适用于中高阻尼和近频信号。

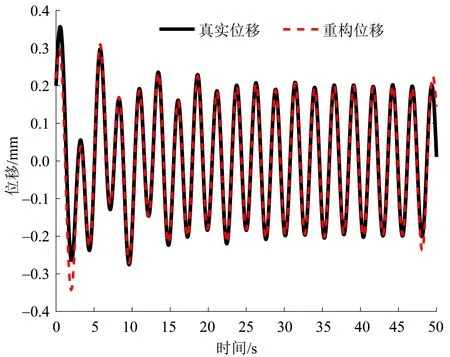
图6 中高阻尼和近频下的位移重构结果图Fig.6 Estimated displacement at medium and high damping and near frequency

3.2 剪切层模型验证

考虑一个10 层剪切层模型（Wang et al.，2020），所有楼层具有相同的质量和刚度参数

阻尼假设为瑞利阻尼

其中α= 0.046 3 s-1，β= 1.625 × 10-3s，M，K分别为质量和刚度矩阵。在第一层施加随机荷载p(t)，其功率谱Sff(ω)为

并按照如下形式生成

其中ϵj表示［0，2π］均匀分布的随机数。结构初始处于静止状态，根据Newmark 法，可以计算其位移和加速度响应，其中，第1层的加速度频谱见图7。将第1 层的加速度仿真数据（采样频率为200 Hz，采样时长为50 s）用作位移重构，而第1 层的位移仿真数据作为真实位移，用于验证位移重构精度。同样，也考虑3.1 节中的两种位移重构方案，其结果见图8。

图7 剪切模型第1层加速度信号频谱图Fig.7 Spectrum diagram of the acceleration for the first layer of shear model

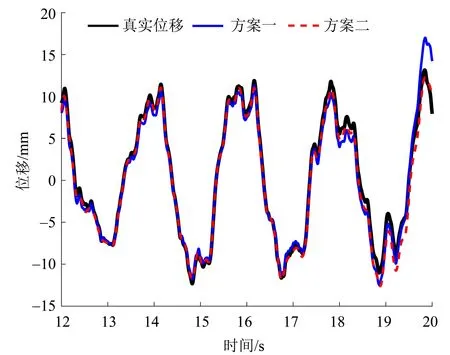
图8 不同方案的第1层位移重构结果Fig.8 Estimated displacement by scheme I and scheme Ⅱ for the first layer of shear model

可以看出，方案二比方案一的重构位移更接近真实位移。此外，还计算了两种方案的位移重构的RE 和COR，结果见表2。尽管两种方案的位移重构精度均较高，方案二的相对误差不到方案一的1/10。因此，有限带宽信号分解确实能提高如图5 具有多个主频峰值（或宽频）信号的位移重构精度。

表2 剪切层模型两种位移重构方案的误差Table 2 Errors of scheme I and scheme Ⅱ for shear model

4 实验测试

为了进一步验证所提方法的实用性，设计了一个4 层框架实验。该4 层框架由钢制成，柱与楼板之间通过焊接连接。4 个加速度传感器分别装在4 层框架的每1 层以测量加速度数据，一个位移传感器用以获得第4层框架的位移数据。实验布置如图9所示。

图9 4层框架实验装置图Fig.9 Diagram of experimental setup of four-layer frame

实验过程中采用晶明动态信号测试系统对4 层框架结构的振动信息进行采集，通过使用橡胶锤锤击第4 层框架来产生一次性的冲击激励，采集系统自动记录过程中的加速度与位移信息，采样频率为200 Hz，采样时长约为127 s.

考虑使用第4层的加速度数据重构位移，并与位移计的测量数据对比。第4层的加速度频域特征如图10所示，具有多个主频峰值，属于宽频信号。采用本文提出的有限带宽位移重构方法（即3.1节的方案二），可得到如图11 的位移重构结果。显然，重构位移与位移计的测量结果十分吻合，表明本文所提方法确实能用于实际结构的宽频位移重构。

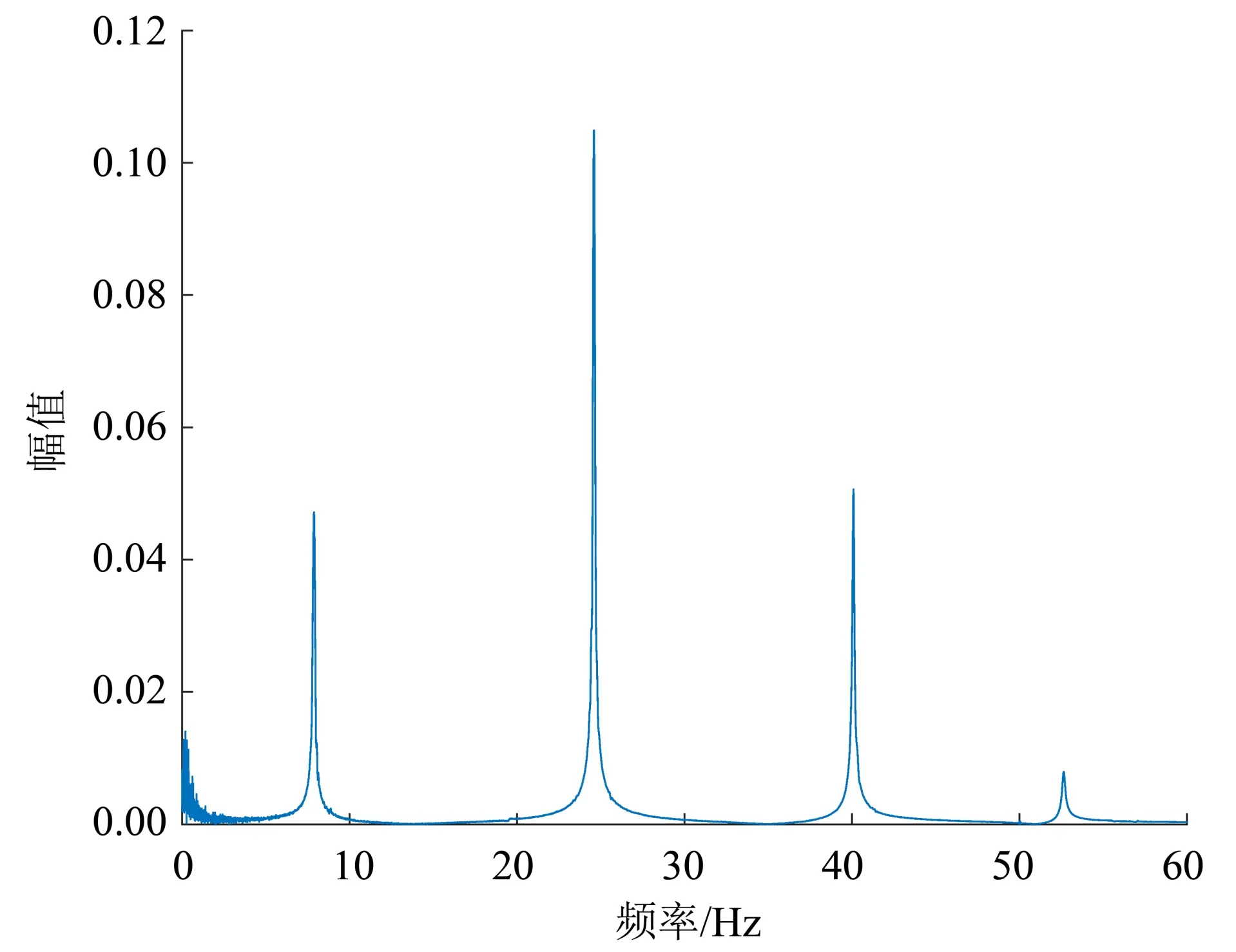
图10 框架结构第4层加速度信号频谱图Fig.10 Spectrum diagram of the acceleration signal in the fourth layer of the frame

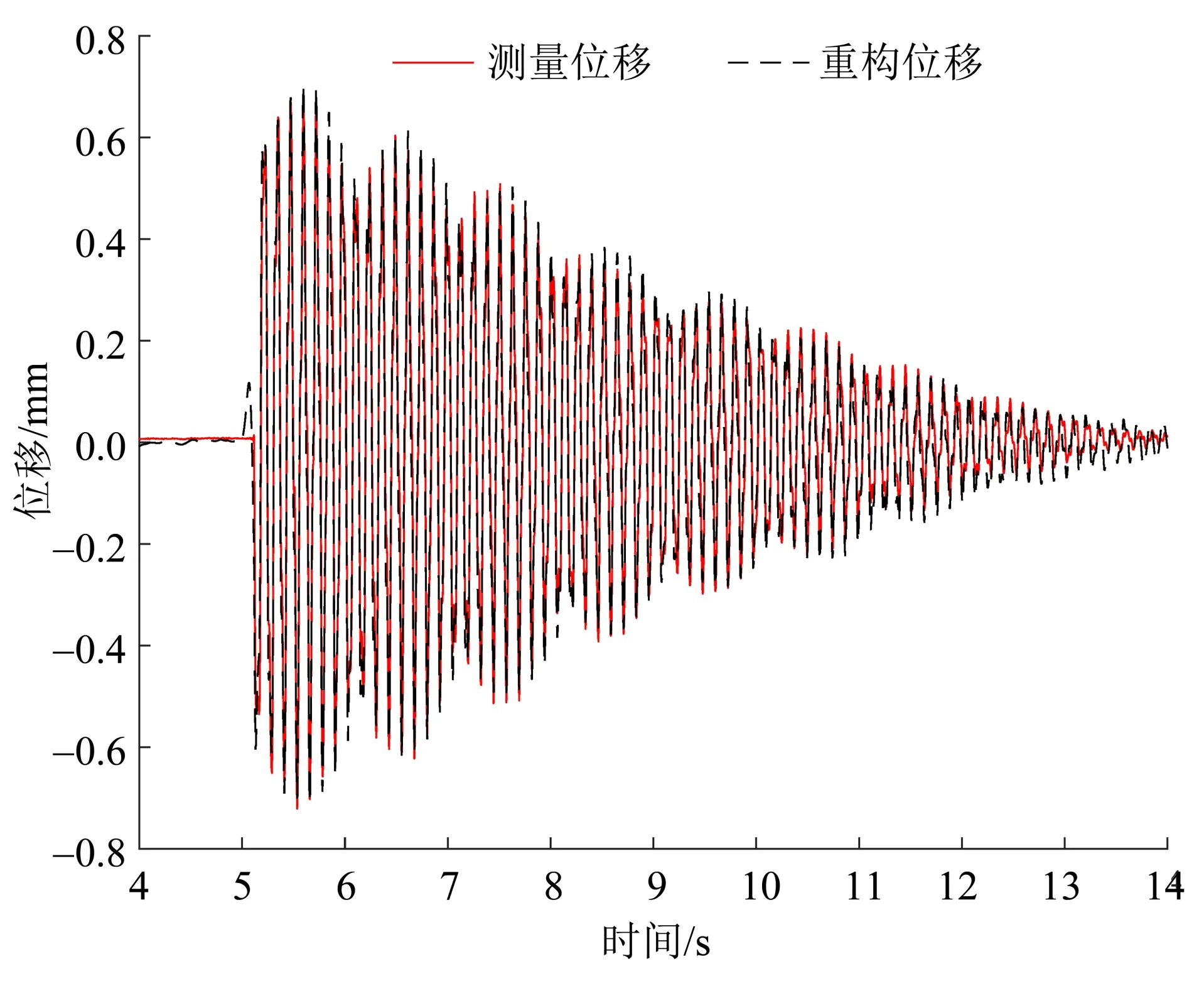
图11 框架结构第4层位移重构结果Fig.11 Displacement reconstruction results of the fourth layer of the frame

5 结 论

基于加速度积分和正则化的位移重构方法很好地克服“低频漂移”现象，但难以处理宽频信号。本文通过进一步引入有限带宽信号分解，提出了一种新的时域宽频位移重构方法。数值和实验算例研究表明，该方法确实能够从宽频加速度信号中准确重构结构的位移信息。