基于NFM-BOK波形的低检测概率通信技术
孙志国, 沙钰彭, 宁晓燕
(哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001)
0 引 言
低检测概率(low probability of detection, LPD)通信技术是认知电子战的核心关键技术,同时也是提升通信隐蔽性能的重要手段之一[1]。与低截获概率(low probability of interception, LPI)相比,LPD通信对信息传输过程中的安全性要求更高,本质上是选择适当波形基和配置合适参数,实现降低LPD波形与背景信号(高斯白噪声)在变换域上的差异特征,使差异特征达到最小的目的[2],根本目的是提升系统的隐蔽性能。
当前,就波形层面而言,频谱扩展技术可以分为以下4类,即直接序列扩频(direct sequence spread spectrum, DSSS)技术、跳频扩频(frequency hopping, FH)技术、切普扩频(chirp spread spectrum, CSS)技术、正弦扩频(sinusoidal frequency spread spectrum, SFSS)技术[3]。随着检测技术的日臻成熟与完善,传统隐蔽信号在变换域中携带的信息易暴露的缺点也日益明显[4]。例如,直接序列——二进制相移键控(direct sequence-binary phase shift keying, DS-BPSK)信号在大信噪比(signal to noise ratio, SNR)时循环相关特征十分明显。在满足波形的距离、SNR、误码率(bit error rate, BER)等基本通信指标的情况下,给定适当能量,可以得到该侦收机的SNR,进而得到在该SNR下的信号特征。LPD通信波形的选取,既要兼顾通信的性能,也要考量波形的特征[5]。
针对上述问题,对于噪声调频干扰做出改进,采用噪声调频(noise frequency modulation, NFM)信号作为波形基,采用二进制正交键控(binary orthogonal keying, BOK)实现NFM-BOK通信[6]。首先在时域上截取一段高斯白噪声,然后使其通过带通滤波器,得到时频限高斯噪声,通过将其与DS-BPSK信号做对比,分别得到在二者Pe=10-4下的SNR1和SNR2,接着对比噪声调频二进制正交键控(noise frequency modulation-binary orthogonal keying, NFM-BOK)信号和DS-BPSK信号分别在SNR1和SNR2下的功率谱域和循环相关域内的聚敛性,从而对二者的通信性能和LPD性能进行综合分析和对比评判[7]。
本文第1节介绍已调信号的数学模型和通信系统模型;第2节介绍已调信号的波形似然函数和通信性能分析;第3节给出已调信号的变换域分析和聚敛性分析;第4节介绍已调信号的数值仿真与性能分析。
1 NFM信号及NFM-BOK通信系统
NFM-BOK通信系统是以NFM信号为波形基,采用BOK作为载荷方式,以相干解调作为解调方式的通信技术。
1.1 已调信号数学模型
如前所述,时频限高斯噪声调频信号波形s(t)如下所示:
(1)
式中:A为信号幅度;f0为载波频率;0≤t≤T;b为双极性载荷信息;KFM为时频限高斯噪声的调频斜率;n(τ)是均值为μ、方差为σ2的高斯噪声。
高斯噪声的波形基本不规律,其幅值、频率和相位难以确定。本文所使用的高斯噪声服从正态分布,对于任意高斯噪声,其概率密度函数[8]为
(2)
高斯噪声在环境中处处存在,往往会被非合作方所忽略,因此选择高斯噪声作为基带波形样本进行传输,非合作方难以对其进行侦测[9]。
当发送信息b取1时,发送NFM-BOK波形为
(3)
当发送信息b取0时,发送NFM-BOK波形为
(4)
在这种情形下,分别用调频指数的正负代表传递数据是1或0。
对比在雷达干扰中常用的噪声调频干扰信号,可以得到mfe=KFMσ/Bn=B/Bn为有效调频指数,B为信号带宽,Bn为调频噪声带宽。当B≫1时,可以认为是宽带调频,即NFM-BOK信号是宽带信号,当取到较大的带宽时,可以认为是一种扩频信号,因而具有隐蔽通信能力,从而得到NFM-BOK的系统增益[10]为
D=B·T
(5)
1.2 通信系统数学模型
基带时频限高斯噪声调频信号的发送,考虑到调频噪声的不稳定性,以及正弦函数取值范围要对应解调相关为线性关系,调频高斯白噪声的均值和方差取值不宜任意选取,否则会造成系统解调误码严重恶化。时频限高斯噪声调频信号的调制模块如图1所示。
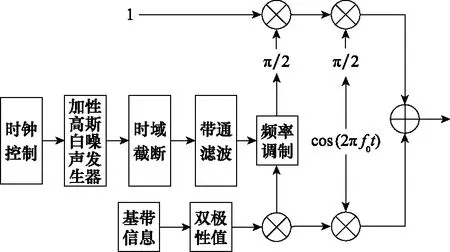
图1 NFM-BOK通信系统调制模块Fig.1 Modulation module of NFM-BOK communication system
时钟控制产生的高斯白噪声在时域上被均匀截取一段,随后经过式(1)所示中心频率为f0、带宽为B的带通滤波器,经过频率调制的信号表达式为
同相支路信号为
正交支路信号为
经过信道后收端为
式中:n1(t)是本文所用的载荷信息的调频高斯噪声,其区别于信道噪声n2(t)。
时频限高斯噪声调频信号的解调模块如图2所示。

图2 NFM-BOK通信系统解调模块Fig.2 Demodulation module of NFM-BOK communication system
当传输信息为1时,同相支路为

(6)
经过低通滤波器,同相支路输出为
本地基带调频噪声样本为
同相支路输出与本地基带调频噪声样本做相关后判决为正。
正交支路为

(7)
经过低通滤波器正交支路输出为
本地基带调频噪声样本反相后可以得到:
正交支路输出与本地基带调频噪声样本做相关后判决为正。
当传输信息为1时,同相支路与正交支路两路均判决为正,因此可以判定传输信息为1。
当传输信息为0时,同相支路为
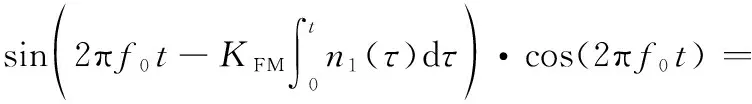
(8)
经过低通滤波器,同相支路输出为
本地基带调频噪声样本为
同相支路输出与本地基带调频噪声样本做相关后判决为负。
正交支路为
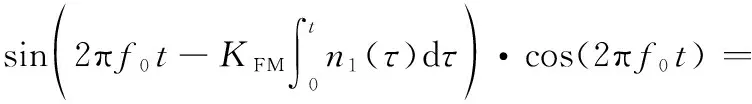
(9)
经过低通滤波器,正交支路输出为
正交支路输出与本地基带调频噪声样本做相关后判决为正。
当传输信息为0时,同相支路判决为负,正交支路判决为正,因此可以判定传输信息为0。
2 通信性能分析
2.1 波形似然函数

(10)
式中:有限长NFM-BOK波形样本的比特能量[12]可表示为
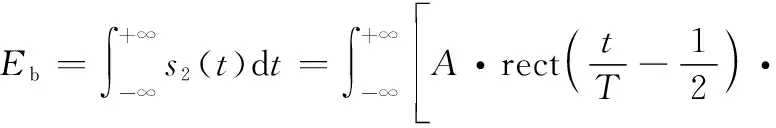
(11)
f(t)的表达式为
(12)
根据上述公式的推导,可进一步得出:
(13)
最终可以得到:
(14)
如图3所示,随着KFM的增大,NFM-BOK带通波形的内正交性ρ+,-趋于0。

图3 NFM-BOK波形样本相关值和调频指数关系曲线Fig.3 Relationship curve between sample’s correlation value and frequency modulation index of NFM-BOK waveform
2.2 高斯白噪声信道下的BER性能
在一般的二元信号波形检测[13]中,假设H0下和假设H1下的接收信号分别为
(15)
式中:噪声n2(t)是均值为0、功率谱密度为Pn(ω)=n0/2的高斯白噪声[14]。信号s0(t)和s1(t)分别为降频信号和升频信号,能量分别为
(16)
(17)
信号s0(t)和s1(t)的能量相等,均记为Eb。假定两个假设是等先验概率,在最小平均概率准则下,似然比检测门限信号η=P(H0)/P(H1)=1。
利用高斯白噪声中一般二元信号波形的判决表达式,可得该二元通信系统表达式[15]为

(18)
在假设H0和H1下,检验统计量l[x(t)]都是高斯分布的,所以各判决概率P(Hi|Hj)决定于偏移系数
(19)
式中:Eb1=Eb0=Eb。
判决概率P(H1|H0)和P(H0|H1)分别为
(20)
(21)
因此,平均错误概率[16]为
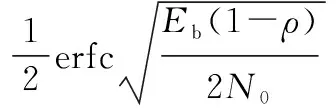
(22)

(23)
当信息载荷b=±1等概率出现时,BER为
(24)
2.3 多径信道下的BER性能
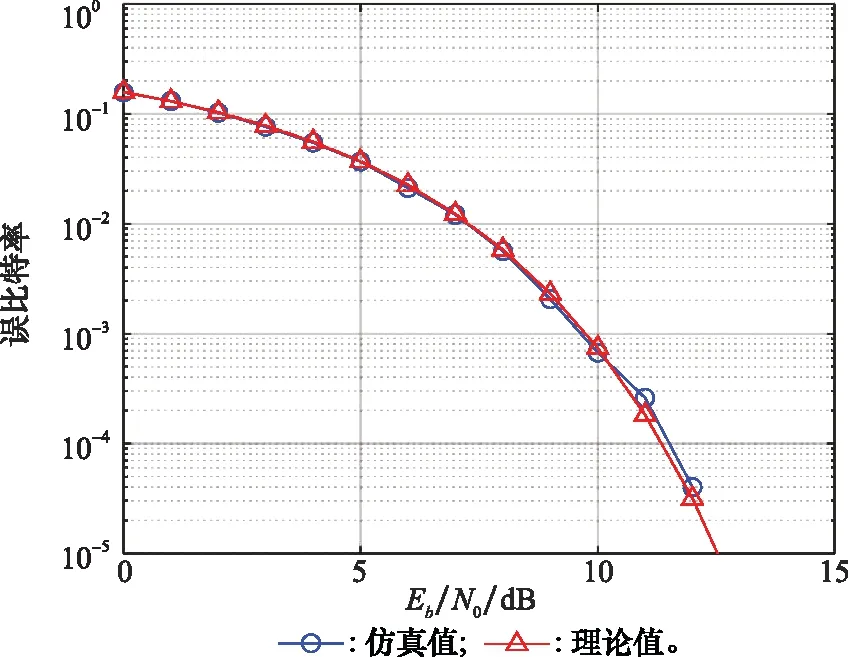
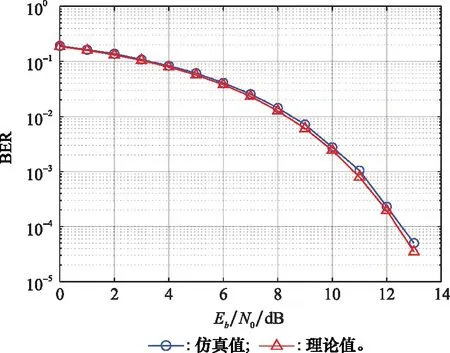
传输信号经过反射和折射后,单向信号成为一组信号。这样的一簇延时|τ| (25) 其均值和方差分别为 (26) (27) 假设m(t)为系数为σ的瑞利随机过程,则接收信号可以表示为 ri(t)=si(t)m(t) (28) 式中:i=1,2。 假设发送的信号为s1(t),那么接收信号r1(t)=s1(t)m(t)与本地信号s1(t)的相关系数ρs1r1为 (29) 接收信号r1(t)与本地信号s2(t)的相关系数ρs2r1为 (30) (31) 代入能量Eb,可以得到多径信道下的BER为 (32) 信号在变换域的聚敛性可以反映信号的LPD性能,定义聚敛性m为 (33) 式中:Y是信号在变换域中的谱函数,Y的峰值与平均值的比值即为聚敛性m,Y值越小,代表信号在该域的LPD性能越好,反之则越差。 通过推导信号功率密度谱,可以确定信号载频和信号带宽范围。信号功率谱可以通过推导信号的傅里叶变换,然后取模求平方来获得。 从信号的功率密度谱中可以得到信号载频值和带宽取值范围,对NFM-BOK进行傅里叶变换,再取模求平方,可得到功率谱[19]。 NFM-BOK的时域表达式为 (34) 其相关函数 (35) 式中:σ2(τ)为函数2πKFM[e(t+τ)-e(t)]的方差,为 σ2(τ)=2[Re(0)-Re(τ)] (36) 假设调频噪声具有带限均匀谱,如下所示: (37) 式中:Bn为调频噪声带宽,则e(t)的功率谱Ge(f)为 (38) (39) 式中:ΔΩ=2πBn为时频限高斯噪声的谱宽。 NFM-BOK功率密度谱的表达式为 (40) 当B≫1时,由NFM-BOK功率密度谱表达式可得 (41) 当B≪1时,由NFM-BOK功率密度谱表达式可得 (42) 循环谱的傅里叶级数[20]可以表示为 (43) 将NFM-BOK代入式(43),可得 (44) (45) 将NFM-BOK的循环自相关函数代入: (46) 可得 (47) 式中:P(f)为NFM-BOK功率谱。 (1) 高斯白噪声条件下的BER 结合第2.2节推导出来的NFM-BOK在高斯白噪声信道下的BER,得到了Pe-SNR的关系。当BERPe=10-4时,推导此时的SNR。 当Pe=10-4时,通过查找Q函数表,可以得到Q函数值的取值范围为3.70≤Q≤3.75,平方后得到13.69≤Eb/N0≤14.062 5。设定调频指数KFM=3×108,载波频率f0=1 000 Hz,调频噪声均值与方差分别为μ=10-4,σ2=10-14,信号码元速率Rb=1 bps,通过上述内容对NFM-BOK和DS-BPSK在相同扩频倍数下(additive white Gaussian noise, AWGN)的BER进行建模分析,在Matlab上对其进行验证。 如图4所示为加性高斯白噪声AWGN下NFM-BOK的BER曲线,仿真结果显示NFM-BOK理论和仿真曲线基本重合,可以认为仿真无误,验证了所提理论的正确性。 图4 AWGN下NFM-BOK的BER曲线Fig.4 BER curve of NFM-BOK under AWGN 如图5所示,当BER为10-4时,由第1.1节推导可知,在相同增益D=30条件下,NFM-BOK的SNR大约为2.6 dB,DS-BPSK信号的SNR大约为-0.3 dB,可知NFM-BOK和DS-BPSK在相同条件下,通信性能相差3 dB左右。 图5 AWGN下的BER对比Fig.5 BER comparison under AWGN 如图6所示,当调频指数KFM分别取3×108、6.2×108、12.6×108、2.54×109时,对应增益D分别为30、62、126、254。可以观察到,当取到合适的增益时,随增益逐渐增大,BER性能越好。 图6 AWGN下不同增益NFM-BOK的BER性能Fig.6 BER performance of NFM-BOK of different gain under AWGN 表1是NFM-BOK和DS-BPSK在Pe=10-4时,不同系统增益所对应的SNR。 表1 SNR对比 由表1可知,随着系统增益增大,DS-BPSK和NFM-BOK 在高斯白噪声信道下通信性能逐渐变好,并且NFM-BOK的抗噪性能劣于DS-BPSK。 (2) 多径条件下的BER 如图7所示,当τ=1 ms时,NFM-BOK在多径信道下的理论和仿真曲线基本重合,可以认为仿真无误,验证了所提理论的正确性。 图7 多径信道下NFM-BOK的BER曲线Fig.7 BER curve of NFM-BOK under multipath channel 如图8所示,当BER为10-4时,τ=1 ms,调频指数KFM取3×108时,NFM-BOK的SNR大约为3.9 dB,DS-BPSK大约为0.2 dB,可知NFM-BOK在对抗多径效应方面弱于DS-BPSK。 图8 多径信道下的BER对比Fig.8 BER comparison under multipath channel 如图9所示,当τ=1 ms,调频指数KFM分别取3×108、6.2×108、1.26×109、2.54×109时,对应的增益D分别为30、62、126、254。可知,随着增益的逐渐增大,BER性能逐渐变好。 图9 多径信道下不同增益NFM-BOK的BER性能Fig.9 BER performance of NFM-BOK of different gain under multipath channel 时频限高斯噪声调频通信技术摒弃了DS-BPSK的隐蔽通信方式,实现了真正意义上的随机性,可以有效提升通信系统的隐蔽性能。 为了提升通信系统的隐蔽性能,防止非合作方对通信信号进行检测,由于NFM-BOK采用时频限高斯噪声作为信息载体,在时域和频域上,其与背景噪声没有区别,即使被检测到,也会增加非合作伙伴的检测难度。 (1) 已调信号功率谱特征分析 下面在相同的带宽、增益、BER所对应SNR的条件下对NFM-BOK的功率谱密度和DS-BPSK的功率谱密度分别做出对比。 如图10所示,通过对NFM-BOK和DS-BPSK的功率谱的仿真对比,在增益D=30下的高斯白噪声信道,当SNR为2.6 dB时,NFM-BOK在载波频率附近有诸多峰值;当SNR等于-0.3 dB时,DS-BPSK没有明显峰值。为了方便对比分析,将DS-BPSK下移20 dB。经对比分析可知,NFM-BOK相较于DS-BPSK在功率谱域隐蔽性能更好。 图10 已调信号功率谱密度Fig.10 Power spectrum density curves of modulated signal 由式(44)可以推导出信号的聚敛系数,如表2所示,随着系统增益增大,DS-BPSK聚敛系数逐渐减小,说明LPD性能也逐渐提高;而NFM-BOK聚敛系数也逐渐减小,说明LPD性能也逐渐改善,且比DS-BPSK数值更小。综合对比NFM-BOK和DS-BPSK的定量定性分析,NFM-BOK相比DS-BPSK在对抗功率谱域检测方面LPD性能更好。 表2 功率谱聚敛性能对比 (2) 信号循环相关域特征分析 确定在信道中是否检测未知信号并识别信号中所承载的信息是主要任务。对于DS-BPSK,在识别到信号存在后,就需要对截获到的信号进行解扩解调处理。在这个过程中,信号载频、初始相位、伪随机码元速率等信息在合作通信中均为已知信息。但是在非合作通信场景下,应该设法使非合作方侦测不到上述信息,以达到隐蔽通信的目的。 结合第3.2节对NFM-BOK循环谱的推导,从信号循环谱中,可以推导出信号统计量随时间变化的规律。在循环相关域中,噪声和干扰对信号的影响减弱,可以从循环谱中识别LPD信号。 如图11所示,图11(a)是NFM-BOK的循环谱f=0的截面。由图11(a)可知,当载频fc=400 Hz时,SNR为2.6 dB,在±800 Hz附近无明显峰值谱线,呈现杂乱无章的状态,这就导致了NFM-BOK的载频估计不准确;图11(b)是DS-BPSK的循环谱,当SNR为-0.3 dB时,DS-BPSK在二倍频处有尖锐峰值。对比图11(a)和图11(b)可知,NFM-BOK相比DS-BPSK在对抗循环相关域方面LPD性能更好。 图11 已调信号循环谱截面Fig.11 Cycle spectrum cross-section of modulated signal 由表3可知,随着系统增益增大,DS-BPSK聚敛特征逐渐减小,说明LPD性能也逐渐提高;而NFM-BOK聚敛特征也呈现减小趋势,说明LPD性能也逐渐改善,且聚敛性比DS-BPSK更小,在小增益处差距更加明显。综合对比NFM-BOK和DS-BPSK的定量定性分析,NFM-BOK比DS-BPSK在对抗循环相关域检测方面LPD性能更好。 表3 循环谱聚敛性能对比 本文结合噪声调频干扰技术、CSS技术、DSSS技术,提出一种新型的隐蔽通信波形设计方案。该方案对噪声调频干扰信号做出了修改,提出了NFM-BOK。由于高斯噪声本身的随机性,与现有隐蔽通信波形相比,NFM-BOK的通信体制呈现非周期性,在各种变换域上,该信号表现出噪声特性。因此,该波形具有良好的LPD性能和LPI性能。仿真结果表明,相比传统DS-BPSK,本文所提NFM-BOK具有以下特征:相比DS-BPSK,NFM-BOK功率谱载频处无明显峰值谱线;相比DS-BPSK,NFM-BOK循环谱在二倍频处无明显峰值谱线;DS-BPSK和NFM-BOK在高斯白噪声信道下的通信性能相差不大;在多径信道下,DS-BPSK通信性能要好于NFM-BOK。3 已调信号变换域聚敛性分析
3.1 功率密度域聚敛特征

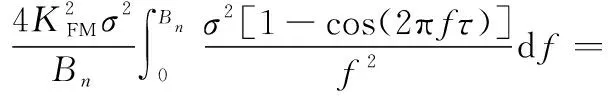
3.2 循环相关域聚敛特征
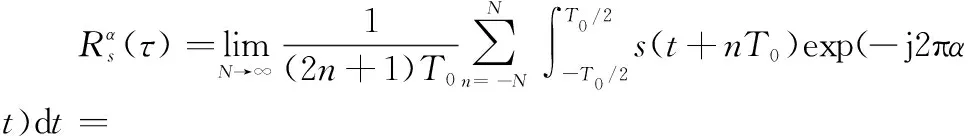
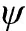
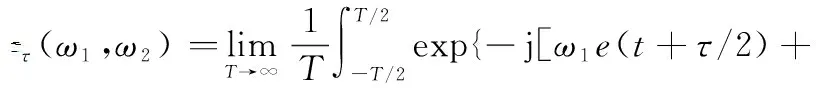
4 数值仿真与性能分析
4.1 通信性能



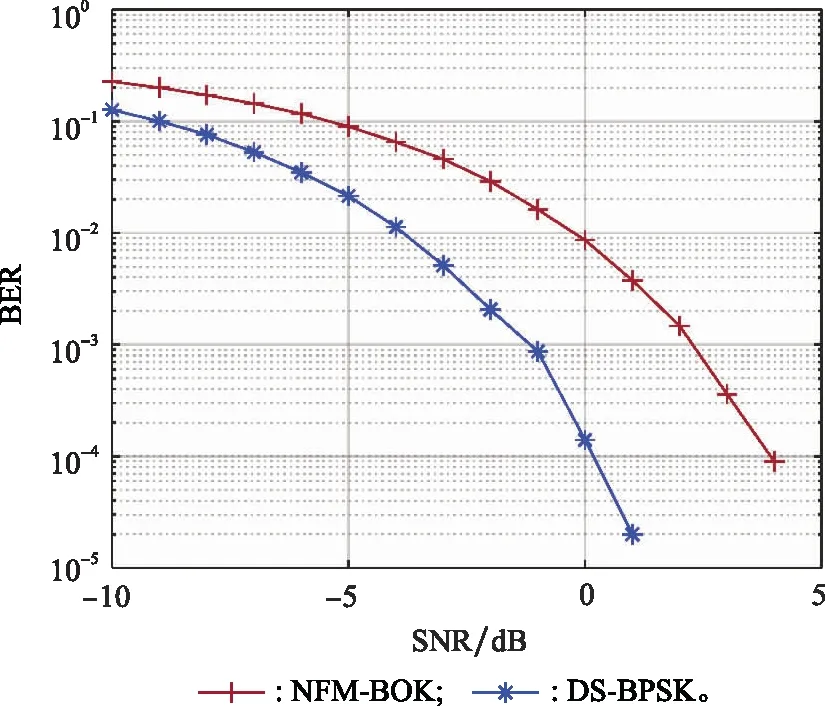
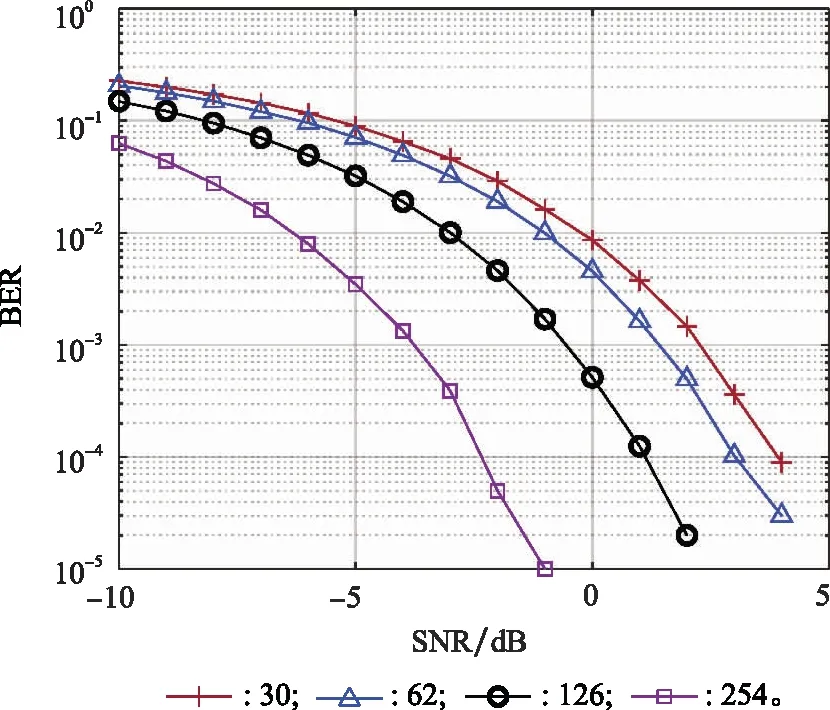
4.2 已调信号各域聚敛特征
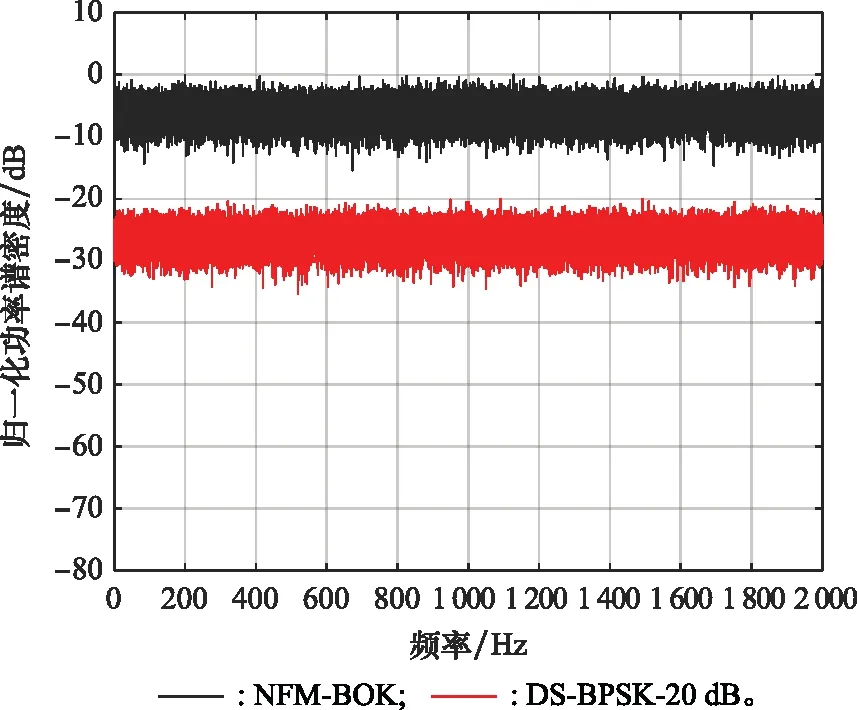



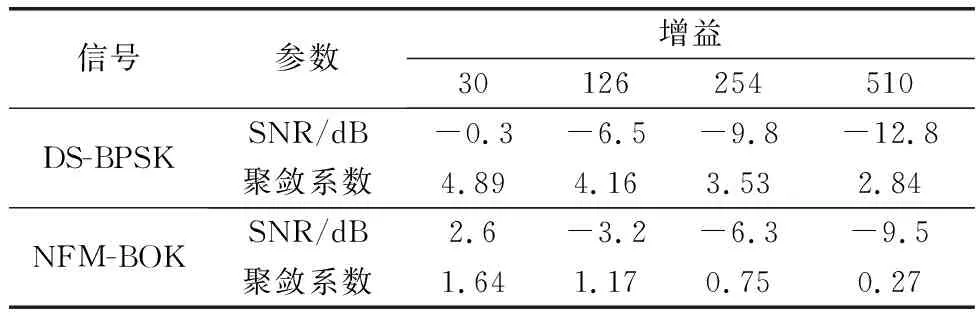
5 结 论

