未知城市环境下的多机协同目标搜索方法研究

刘大千, 包卫东, 费博雯, 朱晓敏

(国防科技大学系统工程学院, 湖南 长沙 410073)

0 引 言

随着智能无人技术的快速发展,具有便携、成本低、机动性强等特点的无人机备受关注,其已被成功应用于智能交通、农业灌溉和战场侦察等应用领域[1-3]。特别是在智能交通领域,以城市环境为背景的多无人机协同组织与优化成为学者研究的热点问题之一,在行人监控、车辆跟踪和道路管理中起着关键作用[4]。因此,本文从城市建模角度出发,主要研究多无人机协同目标搜索问题。

目前,多无人机协同目标搜索主要集中于静态路径规划和动态路径规划两个方面,其中动态路径规划又可分为分布概率预测和群智能决策两类方法,并在近些年涌现出了许多优秀的研究成果。在静态路径规划方面,Nielsen等[5]针对搜索区域边界复杂且区域包含多个障碍物的问题,提出一种凸分解方法,该方法可以有效提高区域覆盖搜索的效率。谢朋志等[6]将搜索区域进行等面积划分,并利用人工势场法计算各无人机的飞行路径。戴健等[7]将多机协同搜索问题转化为子区域上的单机搜索问题,实现了对指定区域的快速搜索。Wu等[8]设计了一种基于连续检测策略的无人机紧急路径规划算法,使无人机能够飞到指定区域并完成对该区域的完全覆盖。在此基础上,他们还将无人机协同路径规划问题转化为大规模的0-1优化问题[9],并利用混合智能算法求解该问题,从而提高了搜索任务的执行效率。然而,实际城市环境存在动态变化,上述方法虽然能够有效解决静态环境中无人机编队协同搜索效率低的问题,但难以应对动态环境所带来的突发情况,具有一定的应用局限性。

在分布概率预测方面,Yu等[10]提出基于概率分布的目标搜索方法。刘重等[11]在此基础上建立了包含建筑信息的数字信息素地图(digital pheromone map, DPM),用于对搜索区域环境的感知。肖东等[12]在DPM的基础上设计了调度信息素,提高了多无人机的协同搜索能力。Tang等[13]提出一种基于矢量信息素的目标搜索方法,通过信息共享对当前时刻的DPM进行实时更新,从而实现了更加高效、准确的目标搜索。黄杰等[14]在目标分布概率图的基础上引入标志位,并利用遗传算法进行优化求解,实验结果表明该方法在保证多无人机飞行路径可行的前提下可提升目标搜索的效率。Liu等[15]提出一种基于回访机制的协同搜索覆盖算法,通过限定信息素传播与挥发系数达到较高的搜索效率,然而建立全局概率图的时效性依赖于城市区域的大小,难以满足实际应用需求,易造成目标逃离和搜索周期较长等问题。

在群智能决策方面,Yao等[16]针对城市环境下的目标搜索与跟踪问题进行建模,并利用改进的灰狼算法(improved grey wolf algorithm, IGWA)进行优化求解,从而为无人机编队规划出更加准确的飞行路径。Carabaza等[17]提出一种基于蚁群优化(ant colony optimization, ACO)的无人机编队搜索方法。与此同时,作者团队还设计了一个基于最短时间搜索的优化机制,使得ACO能够快速获得高质量的水平直线分段无人机飞行轨迹。为了解决未知目标搜索问题,Purbolingga等[18]利用信息素修正ACO算法搜索方式,提高了算法的搜索效率。Zhen等[19]利用人工势场和ACO相结合的方法,提出一种基于人工势场和ACO相结合的无人机群协同任务规划方案,建立了包含4种动目标运动模型的环境概率地图,并通过改进ACO算法实现了多无人机的实时动态决策,在不确定动态环境中得到了较好的搜索结果。在粒子群优化(particle swarm optimization, PSO)方面,Yang等[20]提出一种扩展PSO方法,利用非完整模型更新机器人群的前进速度和旋转速度,以实现运动控制。Saadaoui等[21]提出一种基于局部PSO的多无人机协同搜索(multi-unmanned aerial vehicle cooperative search, MUCS)优化方法,并利用贝叶斯理论进行更新,从而提高了MUCS的效率。然而,这些优化方法受搜索环境影响较大,易陷入局部最优解,导致无人机编队聚集在某一区域搜索,降低多机协同的目标搜索准确率。

综上所述,现有的研究方法在静态路径规划和动态路径规划方面均取得了较好的搜索结果。然而,在实际城市环境中,仍然存在以下问题亟待解决:① 由于无人机视野范围的限制,易因城市区域过大而导致目标难以发现,致使编队搜索执行周期较长;② 面对目标运动状态多样的问题,特别是在未知城市环境中,现有的协同编队策略无法满足搜索区域的均匀覆盖,易造成目标遗漏问题。针对上述问题,本文提出了面向未知城市环境的MUCS方法。具体而言,面对未知城市环境,无法提前获知建筑物、障碍物以及地形地貌信息,充分考虑无人机编队间的信息共享和区域覆盖能力,建立基于共享代价和覆盖收益双重指标的协同搜索模型。在此基础上,引入编队安全距离和移动位移约束条件,确保协同模型的实用性和稳定性。为了得到协同模型的优化解,充分发挥群智能算法在优化求解上的收敛速度优势,改进原有麻雀搜索算法(sparrow search algorithm,SSA)的计算模式。同时,为了发挥无人机的灵活性,本文设定无人机进行变速飞行,以满足目标的动态变化,从而提高多机协同搜索能力。

本文的创新之处如下:

(1) 提出面向未知城市环境的MUCS,旨在解决目标遗漏和搜索周期较长的问题;

(2) 在模型的构建中,设计基于共享代价和覆盖收益的双重指标,确保无人机编队的协同搜索能力和区域覆盖能力;

(3) 在模型求解过程中提出改进的SSA,从而提升协同搜索模型的时效性。

1 基本问题描述

1.1 环境模型

本文以城市环境为背景,利用N架无人机组成编队对未知城市区域Ω进行目标搜索,设定该区域中包含M个运动目标。为了增加目标搜索任务的挑战性,设置多个建筑物、障碍物等不可达区域,并参照文献[22]设置3类不同运动状态的目标供无人机编队搜索,随机初始化各个目标的运动类型。

为了便于描述目标搜索过程,本文对搜索区域Ω进行栅格化等分处理,区域Ω的栅格化地图如图1所示。

图1 区域Ω的栅格化地图Fig.1 Rasterized map of region Ω

该区域的长和宽分别为L和W,单位为m,每个栅格的大小为Δl×Δw。设定每架无人机均等高飞行,且搭载的目标检测摄像头均垂直向下。与此同时,为了保证无人机能够准确识别目标,本文设定各架无人机的飞行高度为Δl,其对应的检测范围为“九宫格”,即以无人机在地面的投影为中心,以一个栅格长度为半径画圆,与之有交集的栅格即为当前时刻该架无人机的检测范围,认定在此范围内目标能够被精准发现。

1.2 无人机模型

假设每一时刻同一栅格最多只存在1个目标,每架无人机利用机载摄像头对区域中的各栅格进行飞行搜索,其行进轨迹由转弯半径和速度所共同决定[23],即

UAVi(t)=[xi(t),yi(t),hi(t)]

(1)

式中:xi(t),yi(t)表示第t时刻第i架无人机在区域Ω中的位置坐标;hi(t)表示航行方向。在基于栅格化的路径规划过程中,本文将无人机在相邻时刻的航行方向设置为八链码方向,其表示如图2所示。具体为:(0) 向前;(1) 向右45°;(2) 向右90°;(3) 向右135°;(4) 向后;(5) 向左135°;(6) 向左90°;(7) 向左45°。无人机模型的具体表达式为

(2)

式中:v为无人机飞行速度;θ为航行角,θ∈[-180°,-135°,-90°,45°,0°,45°,90°,135°]。

图2 目标与无人机的运动方向标识Fig.2 Moving direction identification of target and unmanned aerial vehicle

需要指出的是,在基于栅格化的路径规划过程中,目标仅能在道路上运动,不能穿过建筑物和不可达区域,将目标在相邻时刻的行进方向表示为如图2所示。 具体标号为:(0) 向前;(1) 向右90°;(2) 向后;(3) 向左90°。

2 多机协同目标搜索建模

协同搜索目标要求无人机编队在尽可能少的时间内找出区域Ω中的所有目标,本文假设当目标处于无人机视觉的观察范围内时,即认定无人机已经能够捕获目标[24]。针对单无人机搜索性能差、执行周期较长的问题,提出一种多无人机协同优化模型,以提高多无人机的协同搜索能力,MUCS的整体架构如图3所示。图3中,蓝色长方体为建筑物,白色矩形框为不可达区域。

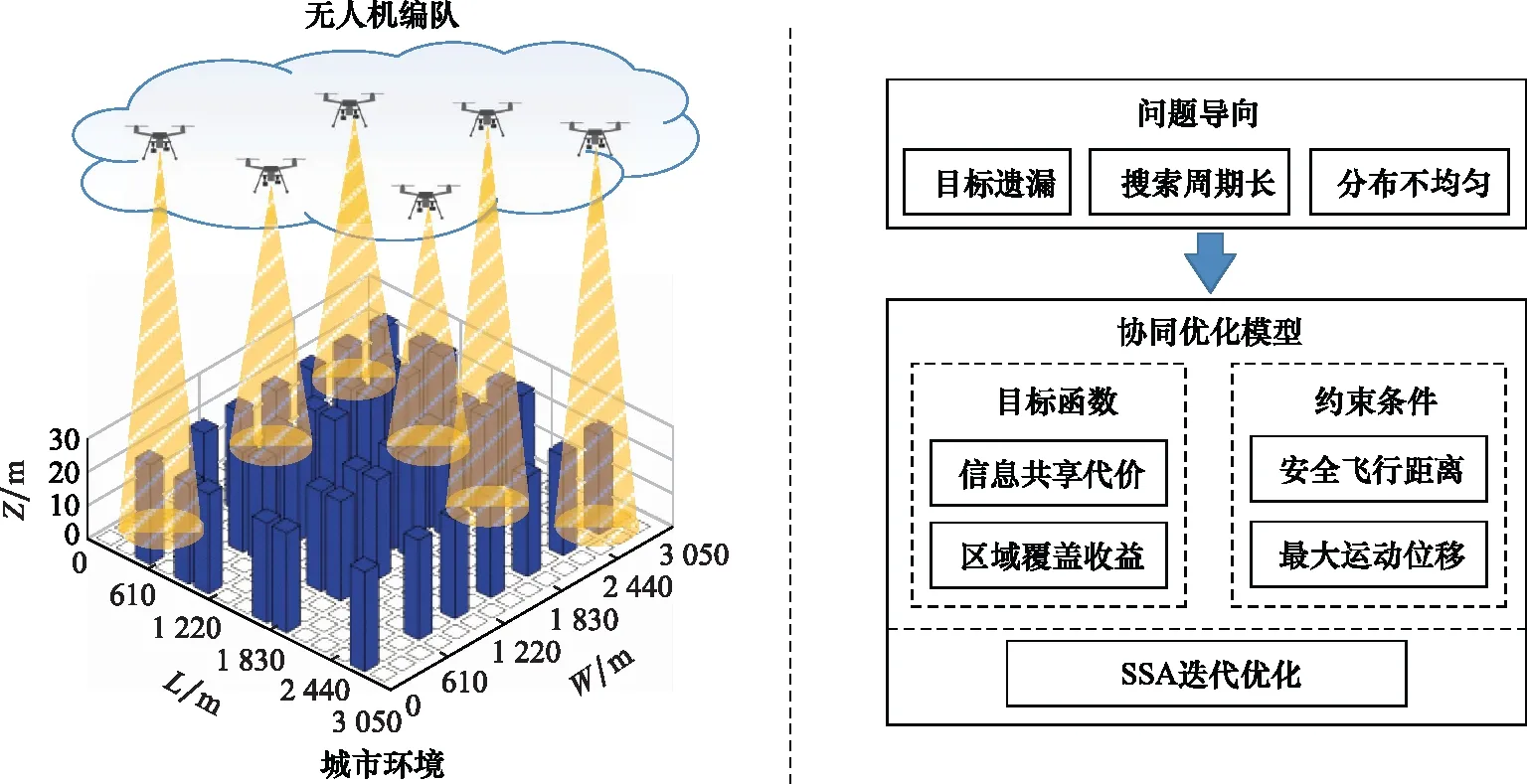
图3 MUCS的整体架构Fig.3 Overall architecture of the MUCS

具体协同搜索过程如下:① 设计目标函数。本文旨在解决目标遗漏和搜索周期较长问题,因此将编队信息共享代价和区域覆盖收益定义为目标函数,以提高无人机编队搜索能力;② 编队约束。在编队飞行过程中,安全飞行距离和最大运动位移是两个最重要的约束条件,决定着协同模型的实用性和稳定性;③ 优化模型求解。基于上述目标函数和约束条件,建立协同编队优化模型,并在求解过程中,设计改进的SSA进行优化解算,提高模型的时效性。

2.1 目标函数

综合考虑无人机信息共享能力和编队区域覆盖能力,本文将信息共享代价和区域覆盖收益作为目标函数,将代价和收益定义为两个双曲正切函数,计算无人机编队的最优搜索解,这两种函数的具体描述如下。

(1) 信息共享代价

为了保证实时共享搜索信息,无人机编队应尽可能地向区域中央进行收缩,以满足信息传输距离的要求。设单无人机的信息共享代价函数为

(3)

式中:f1为双曲正切函数,用于将无人机与区域中心的距离进行归一化操作(距离范围为[0,1]的值),其函数的图像如图4(a)所示;d表示无人机与指定区域中心的距离;dmax表示最大通信距离;Δd表示缓冲距离,其取值范围为[0,1]。因此,无人机编队的信息共享代价函数为

(4)

式中:di表示第i架无人机与区域中心的距离。

(2) 区域覆盖收益

为了确保发现城市区域中的所有目标,无人机应尽可能地向区域边缘进行扩张,以使多无人机能够均匀分布在城市区域的各个角落,从而提高编队搜索的成功率。设单无人机的区域覆盖收益函数为

(5)

式中:f2同样为双曲正切函数,其函数的图像如图4(b)所示;d′表示无人机与指定区域边缘的距离,dmin表示最小安全距离。因此,无人机编队的区域覆盖收益函数为

(6)

从图4可以看出,信息共享代价与区域覆盖收益之间的取值恰好相反。信息共享是将编队之间的距离最小化,而区域覆盖是将编队之间的距离最大化。本文设计的目标函数旨在保证收益与代价之间达到平衡,既能够保证编队的通信能力,同时还能够保证无人机均匀分布在城市区域中,因此多无人机协同优化模型的目标函数为

F=4F1+F2

(7)

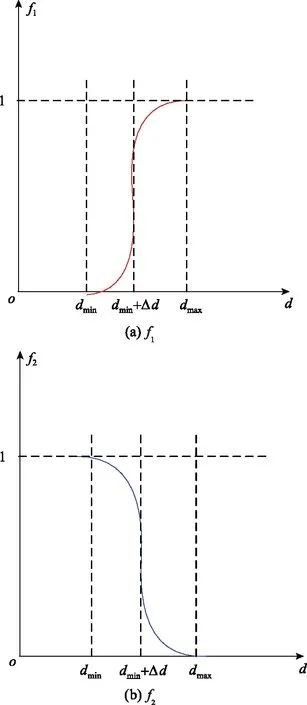
图4 双曲正切函数的示例Fig.4 Examples of hyperbolic tangent functions

图5 无人机编队的收益与代价示例Fig.5 Example of revenue and cost of unmanned aerial vehicle formation

为了进一步说明信息共享代价与区域覆盖收益之间的关系,图5展示了多无人机编队协同搜索的收益与代价。图5中,绿色框表示覆盖收益区域,分布在城市区域的四周;紫色框表示信息共享代价区域,分布在城市区域中心;蓝色框便是城市建筑物。在式(7)中,由于在区域覆盖收益函数F2中已经计算了4个边界点区域的区域覆盖收益,为了保证通信良好条件下,无人机搜索路径在城市区域中均匀分布并达到良好的搜索效率,将目标函数中F1的权重设置为4,平衡信息共享代价和区域覆盖收益。无人机根据自身位移向收益或代价区域移动,达到向中心收缩或向边界点扩张的平衡,从而完成目标搜索任务。

2.2 约束条件

(1) 安全距离约束

在无人机编队搜索过程中,为了避免发生碰撞,对无人机之间的距离进行要求是十分必要的[25-26]。为了简化对无人机编队的安全距离统计的描述,将编队中的无人机进行数字标号,并按升序依次计算两架无人机之间的距离,具体计算公式如下:

(8)

式中:dmin为常数,表示最小安全距离。

(2) 最大运动位移约束

在实际的搜索应用中,无人机的速度应受到限制,以避免在遇到突发情况时发生无人机因惯性导致无法及时避障的情况,进而造成机身受损。由于在实验中设定的目标运动轨迹未知,无人机需要进行变速运动,因此本文对最大运动位移进行限制,具体表达式为

(9)

式中:smax为最大运动位移。

2.3 模型求解

在多机协同搜索过程中,本文建立基于共享代价和覆盖收益双重指标的优化模型,具体表达式为

(10)

为了满足优化模型求解的时效性,引入群智能算法进行迭代优化,群智能算法已被证明适用于许多实际问题,因此,本文选用最新的SSA对式(10)进行求解。SSA是一种非常有效的智能优化算法,它根据麻雀觅食并逃避其他捕食者的行为而提出,且具有寻优能力强、收敛速度快等优点[27-28]。麻雀是群居动物,其捕食(优化)过程主要包含3个步骤:① 发现者搜索食物;② 跟随者争夺食物;③ 边缘个体发现其他猎食者并发出警报。

为了使SSA适用于本文提出的优化模型,对SSA中的3个步骤进行改进,具体数学描述如下。

(1) 发现者:选择50%初始函数F最大的个体作为发现者,其位置更新方式为

(11)

式中:t为当前迭代数;I为一个1×dim的单位矩阵,dim为求解维度;Q为服从正态分布的随机数;Si,j是第i个麻雀在第j维空间中的位置。

(2) 追随者:将剩余的另50%个体作为追随者,其位置更新方式为

(12)

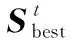
(3) 警戒者:在麻雀搜索食物的同时,它们中的部分会负责警戒,当其他猎食者靠近时,它们会放弃当前的食物,移动到一个新的位置。从种群中随机选择N/4个个体进行警戒,其位置更新公式如下:

(13)

2.4 算法流程

本文利用群智能算法对建立的协同模型进行优化求解,从而获得无人机编队的最优搜索位置,MUCS的主要流程如图6所示。

图6 协同目标搜索流程Fig.6 Process of collaborative target search

MUCS的主要步骤可描述如下:

步骤 1设置无人机初始飞行参数和SSA的初始参数。初始飞行参数包括初始位置、速度范围以及初始航向角等参数。此外,SSA参数包括迭代次数t、维度dim以及候选样本数量n等参数。

步骤 2计算各无人机的备选路径点。结合各无人机的实时位置与八链码方向关系,确定下一时刻的候选位置坐标,输入SSA。

步骤 3在SSA中,首先利用式(7)计算各无人机的目标函数(适应性函数),并按降序排列,从而选出当前时刻无人机编队中的发现者、追随者以及警戒者。

步骤 4分别利用式(11)～式(13)更新发现者、追随者以及警戒者的位置,判断是否满足迭代优化条件。若满足条件,则执行步骤5;反之,则继续执行此步骤。

步骤 5将输出结果与建筑物坐标进行对比,若二者存在重合或包含关系,则证明不满足搜索要求;反之,则输出当前时刻无人机编队的最优搜索位置。

3 实验结果与分析

在MUCS中,无人机飞行参数、目标的初始参数和SSA的参数是十分重要的组成部分,因此本节首先对这些参数进行说明。为了说明MUCS的先进性,本节设计了其与现有方法的对比实验,从定性和定量角度分析说明了所提协同优化模型的有效性。

3.1 实验参数设置

城市区域Ω的实际面积大小为3 050 m×3 050 m,本文利用栅格进行等比例划分,形成61×61个栅格,即栅格的Δl和Δw均为50 m。在该城市区域中,为了增加目标搜索任务的复杂性,共设置了42个建筑物,每个建筑物占用9个栅格(实际面积为22 500 m2),其中还包含了密集建筑群,以更好地模拟城市环境,并利用12架无人机组成编队,对区域Ω进行目标搜索,目标数量设置为9个运动目标,无人机间的最大通信距离dmax为25个栅格,最小安全距离dmin为0.5个栅格,无人机和目标的初始运动状态设置分别如表1和表2所示。此外,SSA的主要初始参数设置如表3所示。

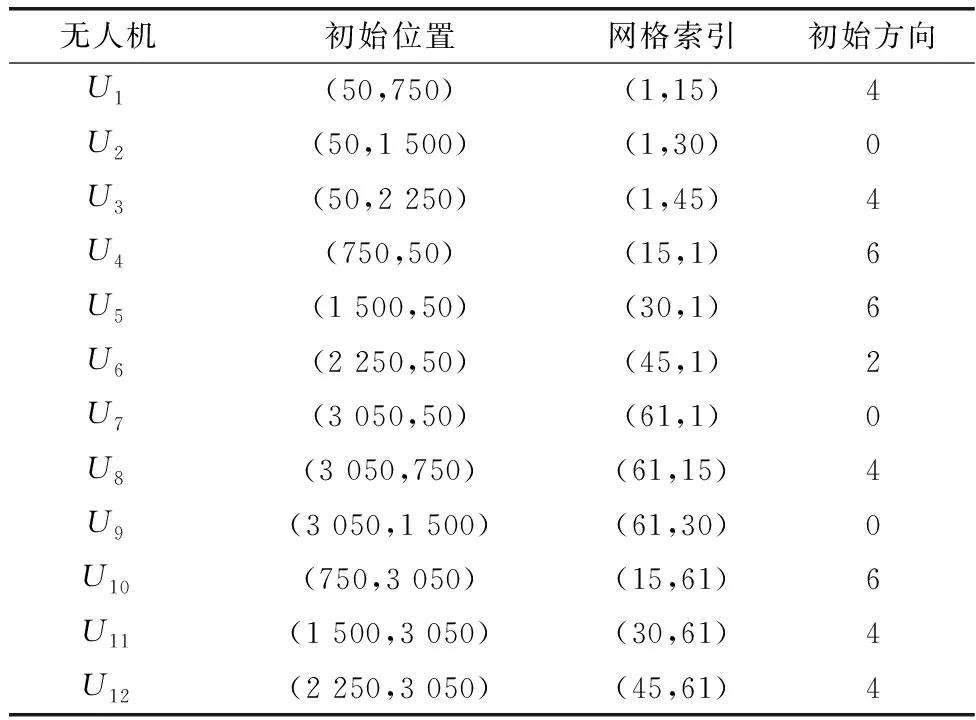
表1 无人机初始状态

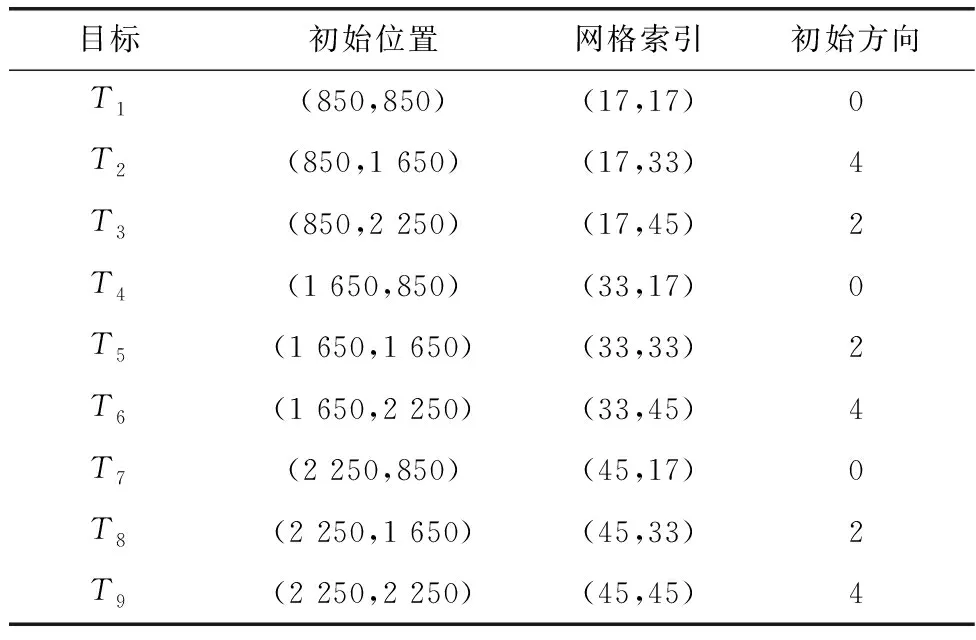
表2 目标初始状态

表3 SSA初始参数

3.2 对比仿真实验

为了验证MUCS的有效性,本节主要将其与较为流行的两类群优化算法,即文献[12]的DPM和文献[27]的SSA进行仿真实验对比,主要评定指标包含搜索时间周期、发现目标数以及区域覆盖率[29-31]。两个方法的具体细节描述为:DPM为典型的数字信息素优化算法,加入调度信息素,并在分布式模型预测控制框架下对其进行优化求解,从而完成目标搜索任务。SSA则为最新群智能算法的代表,在优化求解中模仿麻雀的捕食策略,从而提高目标搜索的准确率。

MUCS、SSA与DPM这3种方法在不同搜索周期下的无人机编队飞行路径如图7所示,其中彩色点为各无人机的搜索飞行轨迹点,蓝色长方体表示城市中的密集建筑物,白色框为城市规划区域。从图7可以看出,3种方法均能够较好地完成目标搜索任务,无人机编队分布在城市区域的各个角落,但无法比较3种方法的编队性能。因此,为了能够清晰展示无人机编队的搜索路径,本节的飞行路径图均为二维平面图,3种方法在不同搜索周期下的飞行路径及目标运动路径分别如图8～图16所示。需要指出的是,无人机能够在高空飞过城市规划区域(白色框),但目标无法进入此区域,仅能在道路上运动,而无人机和目标均不能穿行密集建筑物。

图7 3种方法在400个周期下的3D飞行路径Fig.7 3D flight paths of three methods under 400 search cycles

图8 MUCS在3个不同搜索周期下的无人机运动轨迹Fig.8 Unmanned aerial vehicle motion trajectories of MUCS under three different search cycles

图9 MUCS在3个不同搜索周期下的目标运动轨迹Fig.9 Target motion trajectories of MUCS under three different search cycles

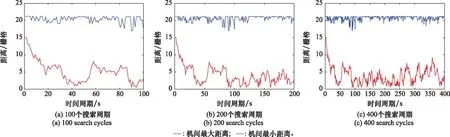
图10 MUCS在3个不同搜索周期下的机间距离Fig.10 Distances between unmanned aerial vehicles of MUCS under three different search cycles

图11 SSA在3个不同搜索周期下的无人机运动轨迹Fig.11 Unmanned aerial vehicle motion trajectories of SSA under three different search cycles

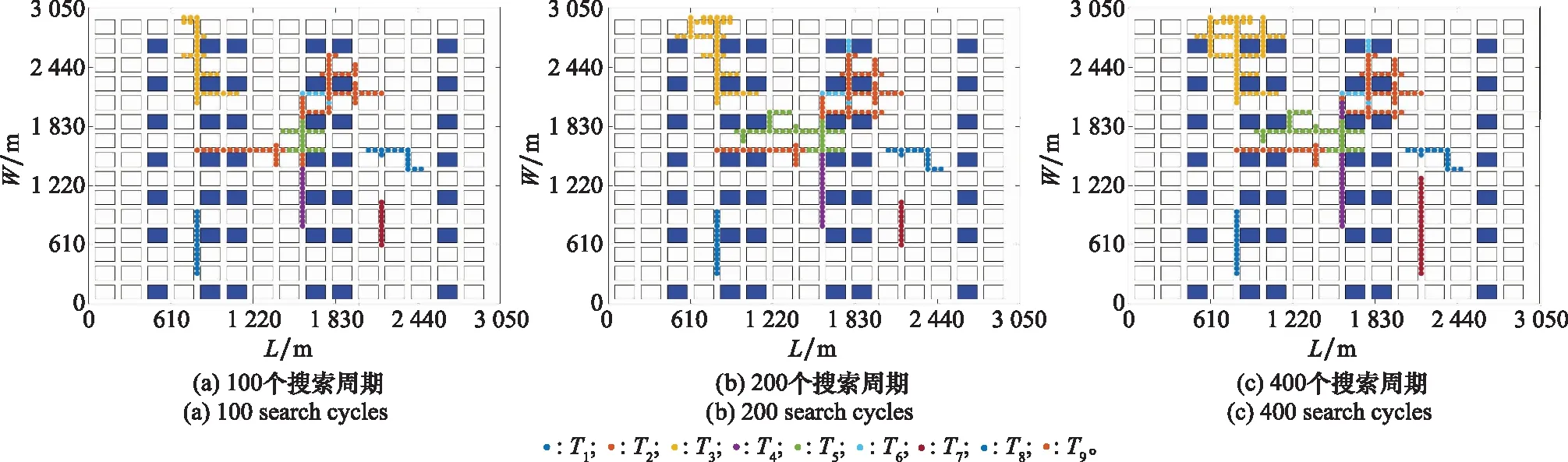
图12 SSA在3个不同搜索周期下的目标运动轨迹Fig.12 Target motion trajectories of SSA under three different search cycles

图13 SSA在3个不同搜索周期下的机间距离Fig.13 Distances between unmanned aerial vehicles of SSA under three different search cycles

图14 DPM在3个不同搜索周期下的无人机运动轨迹Fig.14 Unmanned aerial vehicle motion trajectories of DPM under three different search cycles

图15 DPM在3个不同搜索周期下的目标运动轨迹Fig.15 Target motion trajectories of DPM under three different search cycles

图16 DPM在3个不同搜索周期下的机间距离Fig.16 Distances between unmanned aerial vehicles of DPM under three different search cycles

从图8、图11和图14的无人机运动轨迹可以看出,群智能算法的迭代优化更加合理,执行目标函数更为理想,在整个市区中无人机编队分布得更加均匀。无人机和目标的初始运动状态如表1和表2所示。MUCS和SSA在城市环境中呈现出“区域式”的分布,更加体现了区域覆盖式搜索的群智能性,具体表现为搜索区域覆盖更加均匀、密集,且无人机之间很少有重复的搜索路径。虽然在较短周期内无人机的覆盖范围更小,但随着搜索的不断深入,群智能性逐渐体现,这对于运动目标搜索而言是十分有利的,能够较好地完成目标搜索任务。DPM利用信息素的释放和稀释进行全局图更新,能够保证无人机编队均匀分布在城市的各个角落,具有较高的区域覆盖率,对于静态目标的搜索而言是十分有利的,因此其全局搜索能力更强,区域覆盖率更大。然而,本文主要面向动态目标搜索任务,由于目标位置发生实时变化,若仅要求区域全覆盖是无法满足搜索要求的,因为目标可能在下一时刻出现在无人机已搜索过的区域中,造成目标遗漏现象。

从图9、图12和图15的目标运动轨迹可以看出,MUCS和SSA能够快速捕获目标,致使目标的运动轨迹更少,而DMP的运动目标在较长时间周期下才能发现,导致目标的运动轨迹更长,这进一步说明了群智能算法的区域搜索能力。表4显示了3种方法在400个搜索周期下的发现目标位置坐标,其单位为栅格。其中,“-”表示未发现此目标,表4清晰记录了3种方法搜索到的目标位置,MUCS能捕获所有目标,而SSA则能够发现8个目标,遗漏了3号目标T3。DMP仅发现了7个目标,未能捕获2号目标和8号目标。

另一方面,图10、图13和图16的机间距离记录了3种方法在搜索过程中的无人机间的最大距离和最小距离,其中MUCS和SSA能够较好地利用群优化算法限制机间距离,从而更好地避免了无人机路径存在无人机之间距离大于dmax情况的发生。然而,DMP假设全局通信,并没有对机间距离进行限制,因此该方法的机间距离较大,最大可达到82个栅格,这种情况再一次证明了基于群智能算法的协同编队的有效性。

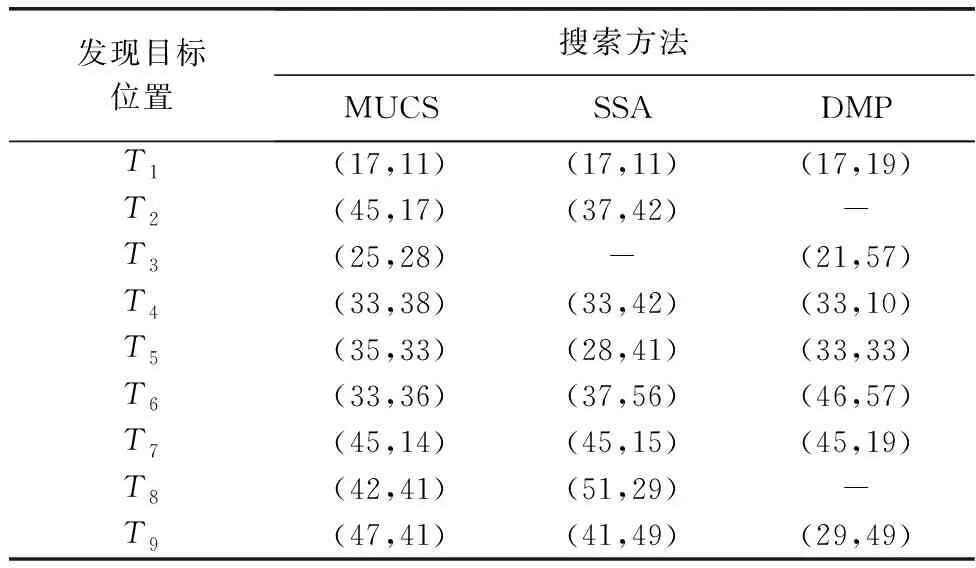
表4 3种方法在400个周期下的发现目标位置

与群智能算法SSA相比,本文提出的MUCS的搜索性能更好,区域覆盖率更高,搜索路径规划更为合理。从图8和图11中的无人机运动轨迹比较可以看出,MUCS能够更好地发挥编队优势,各无人机之间连通性更强,而SSA在400个周期后仍存在大面积未探测区域,搜索效果不理想。这种现象说明了本文利用改进的群智能算法进行模型求解的优势,具有较强的寻优能力。使用该方法时,无论是在区域的边界还是在城市中心,均有搜索无人机的出现,且运动位移较大。

为了能够更加清晰地对比3种方法的性能,分别从搜索周期、发现目标数以及路径覆盖率3方面进行定量分析,对比结果如表5所示。需要指出的是,为了体现实验的公平性,本文对3种方法分别进行了10次独立运行,并取平均结果作为最终的数据统计结果。

表5 3种方法的定量对比

在表5中,当搜索周期同为100时,3种方法的区域覆盖率相当,均保持在20%左右。但DPM的搜索结果更优,能够发现4个目标,这说明采用数字信息素图进行目标搜索在较短的周期内是十分有效的。而当搜索周期达到200时,3种方法的发现目标数均为6个,而MUCS的区域覆盖率为42.57%,SSA的覆盖率为41.53%,DPM最低,仅为39.36%,这也进一步体现了群智能算法的目标搜索能力。在增加100个搜索周期的情况下,发现目标数增加了4个,相比之下,信息素图方法仅增加了2个,且区域覆盖率最低。随着搜索任务的不断深入,从发现目标数方面的对比不难看出,MUCS在400 s时即可找出全部9个目标,且区域覆盖率达到73.58%。而SSA在400 s时能够找出8个目标,DPM在400 s时仅能发现7个目标,且区域覆盖率仅能够达到61.09%。因此,无论是在相同周期下的发现目标数,还是在区域覆盖率上,MUCS均具有一定的优势,这进一步证明了本文所提改进群智能搜索策略的有效性。

3.3 主要参数分析

在组织无人机编队进行目标搜索的过程中,无人机数量和机载摄像头的探测范围为目标搜索任务中的重要一环,直接决定着搜索任务的成败。因此,本文分别对这两个参数进行实验分析,说明所提协同优化方法的有效性。

(1) 无人机数量对搜索结果的影响

在本节实验中,设定目标的数量及运动状态不变,目标数量固定为9个,运动状态如表2所示。为了说明对目标搜索结果的影响,在无人机初始状态方面,本文仍采用均匀分布在四周的策略进行实验,即设定无人机数量分别为4、8、12、16架。为了得到更加可靠的对比结果,将每组实验分别运行10次,并取10次实验的平均值作为最终的统计结果,MUCS在400个周期下的搜索结果如图17所示。

图17 MUCS在400个周期下的搜索结果Fig.17 Search results of MUCS in 400 cycles

从图17可以看出,区域覆盖面积随无人机数量的不断增加而变大。当N=16时,MUCS在400个搜索周期下的区域覆盖率达到78.93%,且能够找到区域中的所有目标,这表明多无人机协同目标搜索的群体智能性。同时,当N=8时,MUCS在400个搜索周期下能够找出8个目标。特别地,该方法在400个搜索周期下能够找出全部的9个目标,这说明了本文所提协同优化模型的有效性。

为了更加清晰地说明无人机数量对搜索结果的影响,表6统计了MUCS在不同周期下的发现目标数和区域覆盖率。表6中,在N=4的情况下,MUCS在400个搜索周期下的区域覆盖率可达到49.84%,占城市区域的50%,发现目标数为4;当N=8时,MUCS在400个周期下的区域覆盖率为67.31%,发现目标数为8;而当N=12时,MUCS仅在400个周期下区域覆盖率即可达到73.58%,即可发现所有目标,这说明无人机数量对目标搜索结果有着重要的影响。无人机数量越多,目标搜索的时间周期越短,区域覆盖率越高。

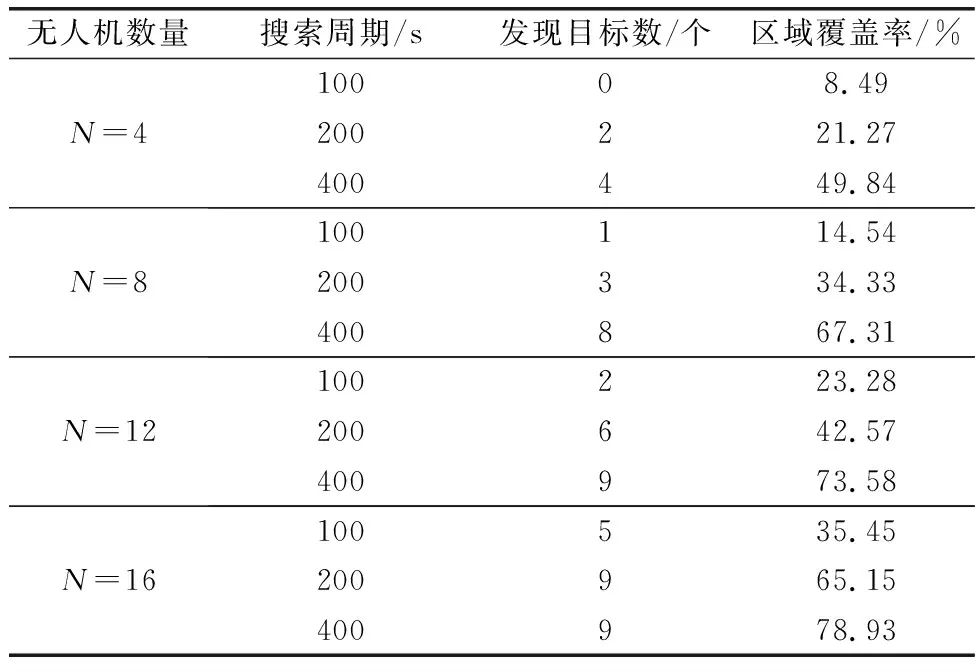
表6 MUCS在不同周期下的搜索结果

(2) 无人机探测范围对搜索结果的影响

无人机探测范围是无人机协同目标搜索的前提,是发现目标的重要保障。本节同样选取9个运动目标、12架无人机组成编队进行实验,它们的具体状态描述如表1和表2所示。为了深入分析无人机探测范围对搜索结果的影响,本节设定不同的探测范围:① 探测半径r为1个栅格,即只有当无人机与目标位置重合时,才视为发现目标;② 设定探测半径为2个网格,即各架无人机探测范围为9个栅格;③ 设定探测半径为3个网格,即各架无人机探测范围为25个栅格。为了得到更准确的结果,同样将每组实验分别运行10次,并取10次实验的平均值作为最终的统计结果,本节仅统计在200个搜索周期下的搜索结果,如图18所示。

图18 不同探测半径下的搜索结果Fig.18 Search results under different detection radius

从图18可以看出,随着探测半径的增大,发现目标数也在不断增加,最大为9个,但区域覆盖面积却随着半径的增大而略有减小。这是因为当探测半径较大时,目标则会被快速发现,待区域中的所有目标均被找到后,编队中的无人机将停留在原地或在小范围内重复飞行,因此区域覆盖率略有下降。在此基础上,表7列出了3个探测半径下的不同周期的搜索结果。

表7 MUCS在不同探测半径下的搜索结果

在表7中,当搜索周期t为50时,3种探测半径的区域覆盖率相当,但发现目标数却相差较大。当探测半径为3时,MUCS能够发现8个运动目标;当探测半径为2时,MUCS在100个周期下能够找到9个目标,且区域覆盖率仅为21.28%,与探测半径为3的搜索结果相当。需要指出的是,MUCS在半径为2时仅在100个周期内已经能够找出全部目标,故而本节并未列出400～600个搜索周期下进行的实验。因此,通过上述定性和定量分析能够得到以下结论:当搜索周期较小时,探测半径越大,发现目标数越多;当搜索周期较大时,探测半径将不再具有优势,甚至在区域覆盖率上略有降低。

4 结束语

本文针对未知城市环境下多机协同目标搜索问题展开研究,提出了基于群智能优化的搜索模型,构建了基于信息共享代价和区域覆盖收益双重指标的协同目标搜索函数。同时,为了增加城市环境的复杂度,本文在城市区域中设定了许多密集建筑物,并设计了3类不同运动状态的目标,使其均匀分布在该区域,从而保证了目标的多样性。在模型求解过程中,为了满足目标搜索的时效性,提出改进的麻雀搜索算法进行优化求解,保证每架无人机均能够得到最优路径可行解。实验结果表明,与当前流行的搜索方法相比,本文提出的MUCS在相同搜索周期的约束下,在区域覆盖率和发现目标数方面均具备较大优势,在保证目标搜索成功率的同时,增强了对未知城市环境的区域覆盖能力。

目前,多无人机协同编队所面临的另一个难点问题是通信链路不稳定问题。在未来的工作中,将从模型的性能出发,重点考虑如何解决无人机之间的局部通信链路和搜索环境动态变化等问题,使得设计的协同模型仍能够在复杂城市环境中完成目标搜索任务。