不确定无卡旋切机变速进给滑模控制
杨素珍
(漳州职业技术学院 智能制造学院,漳州 363000)
人造板是解决全球木材资源问题的重要手段,旋切机作为人造板旋切的主要设备,其控制系统的性能直接决定了人造板加工的质量,研究旋切机控制系统的高性能控制算法具有重要的理论和现实意义。无卡旋切机作为目前木材旋切的主流设备[1],相较于有卡旋切机,木材安装更加便捷,木材的利用率也更高。木材旋切厚度的均匀性是决定人造板质量的关键指标。理想旋切均匀的无卡旋切机的圆木以恒线速转动,而进给系统的切刀以匹配的速度进给[2]。为了实现切刀进给速度的精确匹配,其闭环控制算法十分关键,目前已有自整定比例-积分-微分(Proportion Integral Differential,PID)[3]、遗传算法[4]、PID 神经元网络[5]等方法。但是,由于实际系统不可避免地受到外界干扰,系统也无法精确建模,上述方法未能充分考虑不确定性的影响,控制性能受限,复杂工况下甚至会无法使用。为此,以系统不确定性模型为基础,提出一种恒线速无卡旋切机变速进给滑模控制方法,有效补偿系统不确定性和外部干扰的影响,保证旋切厚度的精度。
1 不确定无卡旋切机的运动学模型
主流无卡旋切机旋切系统的结构示意图,如图1所示。系统主要由圆木驱动系统和切刀进给系统两部分组成,其中:圆木驱动系统为两个同步转动的驱动辊1 和驱动辊2,带动圆木进行恒线速转动;切刀进给系统主要包含一个压尺辊3 和切刀,压尺辊压紧圆木,且与圆木具有相同的线速度。进给系统根据切削条件及厚度不同,带动切刀朝驱动辊方向按照匹配速度变速进给。假设进给系统具备足够的结构刚性,可忽略驱动辊与圆木之间的滑动,则无卡旋切机可得到厚度均匀的旋切板。为了保证进给系统的刚性和精度,进给系统的变速调节通常采用调速电机驱动滚珠丝杆来实现。建立无卡旋切机的运动学模型为[6]

图1 无卡旋切机旋切系统结构
式中:κ为旋切厚度,mm;v为切刀进给速度,mm·s-1;φ为圆木直径,mm;d为驱动辊直径,mm;n0为驱动辊的转速,r·min-1;ɑ为驱动辊1、2的中心距,mm。
可见,恒线速无卡旋切机的变速进给系统是一个时变非线性系统[7],控制器设计难度大。同时,由于结构参数无法精确测量,实际系统不可避免存在干扰、时滞和参数摄动。系统控制器设计时应考虑这些不确定性的影响,建立系统总体不确定性的运动学模型为
式中:ψ为系统总体不确定性项。
2 滑模控制器设计
为了进一步设计控制器,定义目标厚度为κd,则控制误差为e=κ-κd。构造新的控制输入为
将式(4)代入式(1),可得到闭环控制系统的误差方程为
控制器的设计目标是通过确定合适的w,消除系统总体不确定性项ψ的影响,使得系统误差e渐进收敛于原点。滑模控制采用不连续动态控制策略,使系统状态沿着滑模面滑动,从而使系统对参数摄动和外部干扰具有健壮性,而且具有响应迅速、易于实现等优点[8]。
采用趋近律方法设计滑模控制器,定义积分滑模面为
式中:k为非负常数。
对式(6)求导,将式(5)代入可得
滑模运动包括从系统初始状态趋向切换面,直到实现s→0 的趋近运动,以及在切换面附近的滑模运动两个过程。由于滑模控制未限制趋近运动的轨迹,采用趋近律的方法可以改善趋近运动的品质,进而减小滑模抖振[9],取指数趋近滑模控制律为
式中:ε和λ均为非负常数。
通过闭环误差控制系统的误差方程和指数趋近滑模控制律,可使得系统渐进稳定,其证明过程如下。设正定Lyapunov 函数为
不失一般性,假设ψ是有界的,其上界为,即|ψ|≤。对式(9)求导后,将式(7)代入可得
将式(8)代入式(10)可得
由式(2)可知,通过合理设计无卡旋切机的结构参数d和ɑ,可获得圆木的剩余量,很容易保证(φ+d)2≥ɑ2,即 ( ) 0ϑ φ≥。通过合理选择ε的数值,容易使得此时,如果要使得则必须令s=0,即e=0,可见系统存在唯一的最大不变集。根据Lasalle 不变性原理,只要e的初值处于吸引域内,则有即系统是渐进稳定的。
需要注意,系统控制过程中,由式(8)获得的滑模控制器控制量需通过式(4)转化为无卡旋切机进给系统(3)的实际控制量。
3 仿真实验
在MATLAB 环境下进行仿真实验,无卡旋切机的总体不确定运动学模型和滑模控制器采用M 文件编程实现,微分求解器使用ODE45,仿真步长取0.01 s。无卡旋切机的仿真模型参数如下:40 mm ≤φ≤400 mm,d=82 mm,n0=40 r·min-1,ɑ=94 mm,厚度初值取sd=1.4 mm,目标旋切厚度sd=2 mm,不确定项ψ=1+cost+sint。常规PID 控制器和文中控制器的旋切厚度变化曲线对比图,如图2 所示。由图2可知,由于系统存在复杂不确定性,常规控制器无法实现控制目标,而文中滑模控制器有效消除了该不确定项的影响,控制器控制效果较好,上升时间快,超调量和稳态误差均较小。
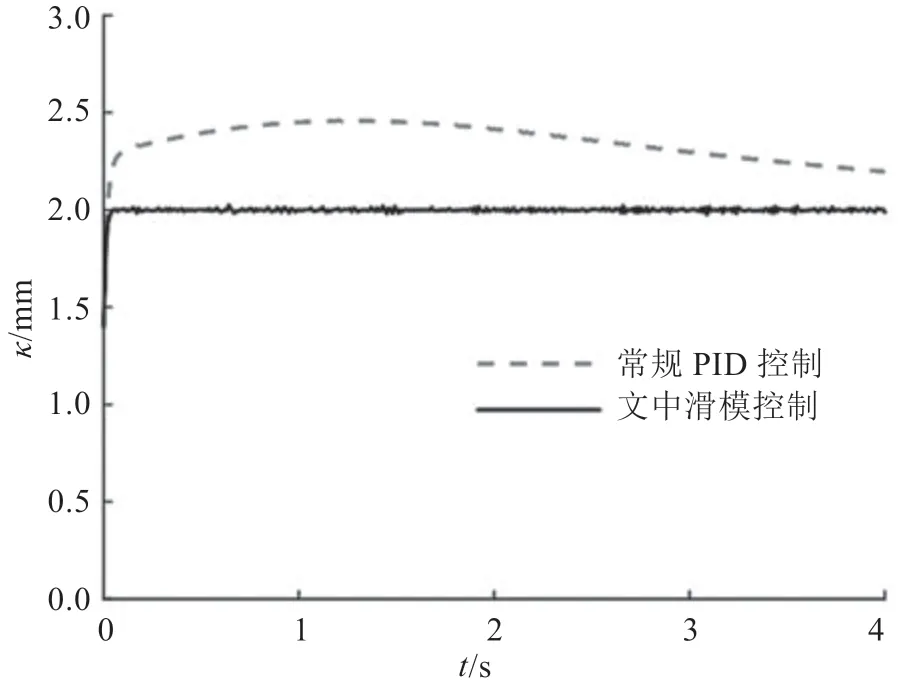
图2 旋切厚度变化曲线
不同目标旋切厚度的速度输出变化曲线如图3 所示,可见控制输入变化平稳,滑模抖振在较小范围内,使用指数趋近律的滑模控制有利于无卡旋切机减小振动,降低能耗。从图3 还可以看出,旋切厚度越小,速度变化量越小。
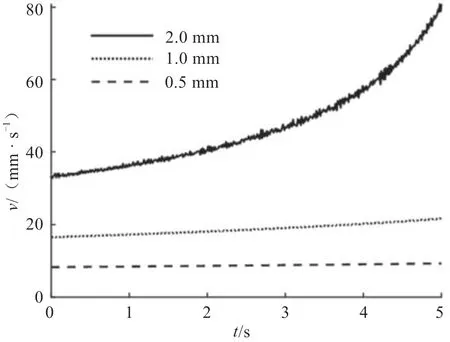
图3 进给速度变化曲线
4 结语
进给系统的精确变速匹配是无卡旋切机实现单板均匀旋切的关键,由于其工作环境恶劣,且结构参数难以精确测量,不可避免地受到系统模型不确定性和外界干扰的影响,控制器设计应予以充分考虑。文章建立了无卡旋切机的不确定误差控制模型,设计了一种基于指数趋近律的滑模控制器,有效控制系统不确定性的影响,并减小滑模抖振现象。在MATLAB 软件环境下,使用M 文件编写无卡旋切机不确定运动模型和文中控制器,进行仿真实验验证。从不同控制器的厚度变化对比和不同旋切厚度的进给速度变化对比结果表明,文中控制器有效提高了系统的控制性能,进给速度变化平稳,实时性好,收敛迅速,控制精度高,适应性强,具备较高的实用性。

