基于数字孪生的刀具磨损监测和预测方法研究
唐艳玲 吴 捷
(苏州大学,苏州 215131)
在切削过程中,刀具状态作为重要因素影响着切削效果。刀具处于磨损状态下会严重影响受作用零件的尺寸精度和表面质量。处于磨损状态下的刀具,其切削力度将显著提升,使得切削过程中零部件表面受到的摩擦力加大,进而导致温度升高[1]。工件表面受高温影响产生热塑变形,使得残余拉应力取代原有的残余压应力。由于刀具切削加工环境多变性及复杂性程度高,如何实现刀具状态的及时、准确、可靠评估成为越来越热门且重要的研究方向。本文将结合数字孪生方法开展刀具磨损监测和预测方面的研究。
1 基于数字孪生的刀具磨损监测和预测模型
刀具会随着切削的进行产生一定程度的磨损,而磨损及切削状态受到切削参数、刀具安装、工件材料等多方面共同影响和作用。在这种情况下,刀具的切割磨损状态呈现出动态化、随机化等特点[2]。因此,为了实现准确监测和预测刀具磨损状态,必须建立与物理刀具多面参数一致的数学模型。以数学孪生理念为基础建立一套切削刀具数学孪生模型,准确模拟物理刀具真实、即时操作状态,为刀具的精准监测打下坚实的基础。
数字孪生机理模型分为4 个子模型,具体包括几何模型、物理模型、行为模型和规则模型。其中:几何模型和行为模型主要宏观反映刀具几何尺寸、切削及刀具磨损退化过程;物理模型和规则模型主要从微观上反映材料应变强化、温度软化效应等特性。
1.1 几何模型
几何模型主要包含刀具角度、刀尖圆弧半径等参数。本文重点研究刀具磨损,因此将选择与刀具磨损相关的刀具几何参数。根据式(1)的刀具磨损率方程可以看出,刀具磨损速率受刀具前后角影响。
1.2 物理模型
刀具及工件的材料属性由物理模型来反映。物理模型也是模拟整个切削加工流程的理论基础,可以反映材料的应力变化、热力学性能等力学性能参数。本文拟选择Johnson-Cook 模型,其表达式为
式中:A、B、C、m、n均为材料特性常数;为等效塑性应变;为等效塑性应变率;为参考应变率;T0为室温;Tm为材料熔点。
1.3 行为模型
行为模型主要表征应力应变、应变率、切削力及切削温度等参量,为后续的规则模型提供一定数据支持[3]。在此应重点把控刀-屑间的接触摩擦和切屑分离准则,以获得更好的行为模型。
1.3.1 接触摩擦模型
刀具与工件切削过程中,工件表面质量及切削形态常常受到刀具与切屑互相作用产生的摩擦影响。本文选用混合摩擦模型来表征接触摩擦情况,其表达式为
式中:μ为摩擦系数;ɑn为接触法向应力。
1.3.2 切屑分离准则
切屑分离准则能够真实反映切削过程中切屑与工件是否完全分离,是整个切削过程中尤为重要的一项判断标准,对孪生机理模型是否完全分离具有决定性作用。由于J-C 断裂准则表达式具备表征性强、可准确反应工件与切屑间的分离等特点,拟选取此表达式进行建模,具体表达式为
1.4 规则模型
为了得到刀具切削行为的详细描述和刀具磨损状态的动态体现,需要在物理层面进行建模分析。基于此,本文以刀具磨损机理为基础实现规则建模,目的是反映刀具磨损退化规则。在选择磨损退化规则前,应确定好与刀具对象适配的磨损机理,依据适合的机理确定出相应的退化规则模型,即
式中:G、D均为切削条件常数;υ为切削速度;f为进给量;e为切削活化能常数;R为温度常数;T为通用气体常数。
2 数据模型的构建方法研究
数据作为整个孪生模型的基础及核心,是整个刀具规范作业流程的保障,因此对数据的挖掘与分析是整个实际作业与孪生模型之间虚实结合的前提。但是,数据获取的状态也存在一定弊端,因为传感信号仍需要作业人员进行操作获取,所以人工因素影响也需要纳入考虑范围[4]。
随机森林模型作为一种广泛应用的集成学习模型,其基础学习通常为决策树,实现原理为有放回地选取训练样本子集和随机选择不同训练特征子集,从而构建大量基础学习模型。
步骤一:有放回地对样本抽样,实现每棵树不同的训练样本。
步骤二:对所有样本中的特征参数进行特征子集选取,用来实现各决策树的输入特征。由于各决策树训练样本及特征子集存在差异性,最终会形成不同训练状态的决策树。
步骤三:对所有决策树进行加权融合,最终集成一个学习模型。
基于实际的刀具磨损监测实现特征参数的优化选择,提高模型的评估效果。提出对随机森林模型的建立过程进行改进,以相似度为依据改进训练样本的扩充方式。在选择随机森林模型样本时,常用训练样本囊括实验过程中的全部历史数据,用以搭建全局变量模型。拟以相似度为依据,改善模型训练样本的构建方式,扩充训练样本数据,达到训练样本更集中于样本局部空间的效果。
当前刀具状态特征序列与所有历史状态特征序列之间的相似度表达式为
式中:X=(x1,x2,…,xn)为当前状态特征序列,历史状态特征序列则用N来表达,两序列的距离函数用dis(X,Yi)来表达。
距离函数通常取为欧氏距离,即
根据相似度计算历史状态特征序列被选入训练样本的概率为
在随机森林模型的训练过程中,对于每棵决策树,以所有历史状态p作为总体样本,从中有放回地抽取k个状态特征序列加入训练样本。根据此种数据集成方式,原始训练样本中新增k个个体(新增的个体离当前状态较近),训练样本会随着新增个体数量越来越向局部空间集中倾斜,也可提升相应的局部空间预测精度。
3 刀具磨损监测与预测方法训练及验证
通过构建的刀具磨损寿命周期内特征参数数据集,对建立的刀具磨损监测与预测模型进行训练验证,确定模型参数。
3.1 样本数据选取
以使用时间为依据将构建的刀具磨损全寿命数据按20 h 间隔拆分为20 组参考样本,使用时间分别为100+i,120+i,…,780+i,其中i=1,2,…,20。每组样本包含35 个状态特征序列,并以第1 ~15 组样本作为剩余寿命预测模型的训练样本集,第16 ~20 组样本作为剩余寿命预测模型的测试样本集。表1 为第1 组样本中不同使用时间刀具磨损的特征参数。其中:Imp代表启动时的平均电流;Idp代表加速运转时的平均电流;Impp代表匀速运转时的平均电流;Idpp代表减速阶段的平均电流;FC代表经过归一化处理的切削最大值;Dpe代表经过归一化处理的切削最大直径;RUL 表示剩余使用寿命(Remaining Useful Life)。
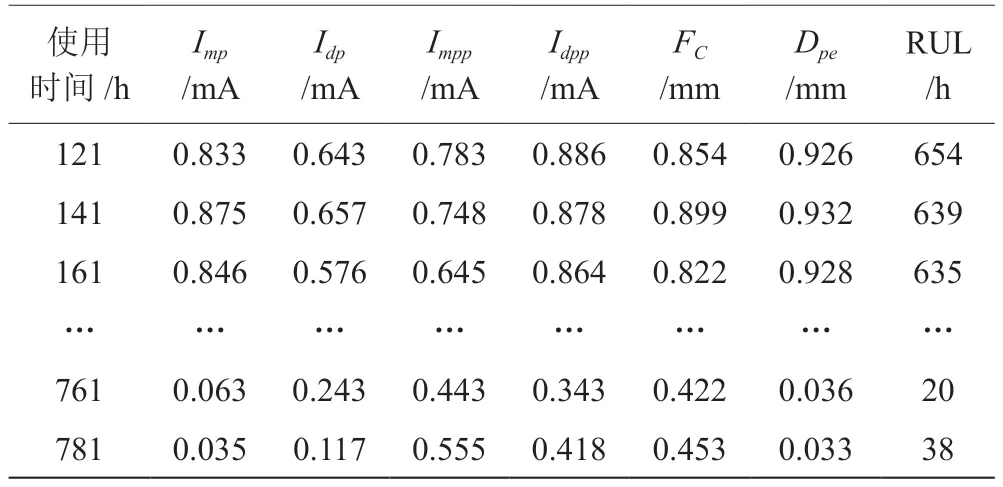
表1 第1 组训练样本
3.2 评估效果评价指标
通常情况下,借助一系列精度指标来评估刀具磨损预测模型的评估效果,主要采用平均绝对误差(Mean Absolute Error,MAE)、平均相对误差(Mean Relative Error,MRE)、误差平方和(Sum of Squared Error,SSE)等[5]。
为实现良好的评估效果指标评价,预测样本剩余寿命的观测值序列假设为NRUL={N1,N2,…,NM},评估值序列假设为NRUL*={N1*,N2*,…,NM*},预测样本长度为M,相应的模型预测误差为
平均绝对误差为
平均相对误差为
误差平方和为
为对已建立的模型评估效果开展评价,本文选用评价指标为MAE 及SSE。除上述两项评价指标外,另提出误差代价评价指标评估模型效果。该误差代价评价指标定义为
在预测模型存在误差的情况下,为实现良好效果需要更早实现提前预警。相同的绝对误差,滞后报警所需代价必然高于提前报警。
3.3 评估效果验证
利用构建的样本集验证建立的评估模型效果。在此选取数量为N的样本,每次有放回地抽取n个样本,抽取的样本分别作为n个学习机的训练样本,在每个样本中随机选取p个特征参数作为学习机的输入节点。
为了了解不同模型参数对评估效果产生的影响,使用MAE、SSE 和cost 这3 个指标对各种情况下的评估结果进行评价。利用第1 ~15 组样本作为训练样本集,评估第18 组样本剩余寿命,模型分别选择n=10、20、50、100 和p=3、6、9、15,以研究不同模型参数对评估效果的影响。
越大的模型参数展现的模型效果并非越好。根据结果不难发现,当n=20、p=6 时展现出来的模型效果最佳,评估结果如图1 表示。

图1 n=20、p=6 时随机森林模型预测结果及误差
对于相对单一的神经网络模型,可以通过增加基础学习机数量的方法进一步提升刀具磨损改善效果,但这一问题因每个学习机对末端状态训练量不足仍未得到有效解决[6]。在对预测结果使用MAE、SSE 和cost 这3 个指标进行评价后,结果显示:学习机对于测试样本附近的感应会随着样本量的增加产生一定增强,预测效果得到相应改善;随着样本增加量超过原始样本后,模型将对局部空间的偏移过于敏感,反而降低了模型的评估效果。通过评估结果可知,经过误差修正,双层预测模型的绝对误差已被减小至2 h 以内,说明所提算法具有一定准确性。
4 结语
利用数字孪生模型,对刀具磨损和预测的相关方法进行研究。本文的相关工作证明,基于状态特征序列与历史状态特征序列之间相似度的随机森林算法,应用于刀具磨损预测的准确率较高。

