钢管混凝土拱桥拱肋模拟方法探讨与分析

叶 伟，王 雷，王 同，段银龙

（广东省交通规划设计研究院集团股份有限公司，广东 广州 510507）

0 引 言

钢管混凝土拱桥具有承载力大、施工快速、后期维护费用低、抗风抗震性能好等众多优点[1-2]，日益受到人们的重视和青睐。由于钢管混凝土拱桥杆件多、受力复杂，一般通过有限元程序来进行模拟和计算[3]。影响有限元计算结果准确性的关键往往在于拱肋的模拟[4]。拱肋常用的模拟方法有刚度叠加法和统一理论法，前者无法模拟钢与混凝土之间的套箍效应[5]，后者不能进行施工阶段分析，两者都有一定的局限性，对于哪个模拟方法更合理尚无定论[6]。目前，基于不同模拟方法对钢管混凝土拱肋在刚度取值和结构力学行为等方面的研究还不够完善[7]，有必要进一步分析，给此类桥梁设计提供参考或借鉴。

本文首先针对几种典型的钢管混凝土模拟方法进行对比分析，综合考虑统一理论法与刚度叠加法的优点，按照统一理论双单元法的思路来建模分析；之后根据国内两本现行公路钢管混凝土拱桥规范，针对拱肋轴向刚度和抗弯刚度的差异，建立误差分析模型进行比较。最后，以净跨径390 m 中承式钢管混凝土拱桥为工程背景，分别基于统一理论法、统一理论双单元法和刚度叠加法建立有限元模型，探讨分析在成桥态恒载作用下，不同模拟方法对钢管混凝土拱桥主拱轴力、位移和稳定性的影响。

1 拱肋的模拟方法

1.1 典型模拟方法

钢管混凝土拱肋的典型模拟方法有刚度叠加法、统一理论法、截面换算法和纤维单元法[8-10]，它们之间的比较见表1。

表1 拱肋模拟方法的比较

刚度叠加法认为钢管混凝土由钢管和混凝土两部分组成，其刚度由两者叠加而成，《钢管混凝土拱桥技术规范》（GB 50923—2013）（下文简称2013 规范）应用了此理论；统一理论法的核心思想是将钢管混凝土视为由一种材料组成的统一整体[11]，推导出组合截面的本构关系，是《公路钢管混凝土拱桥设计规范》（JTG/T D65-06—2015）（下文简称2015 规范）采用的理论；换算截面法将两种材料合二为一，把混凝土截面按刚度等效的原则换算成钢材截面，以单一的材料来模拟；纤维单元法按照化整为零的思路，将钢管混凝土拱肋实体精细划分为有限个钢纤维单元和混凝土纤维单元来模拟整个拱肋截面的刚度。

由表1 可知，这四种模拟方法都有一定的局限性。刚度叠加法无法考虑钢管的套箍作用，只限于弹性范围内分析，且无法模拟钢混凝土组合结构的材料非线性。统一理论法虽然能考虑钢与混凝土之间的相互作用，但无法模拟整个施工过程，也不能读取钢管初应力。换算截面法和纤维单元法分别存在结果误差大和计算难度高的问题，较少应用于大跨桥梁。

1.2 统一理论双单元法

为弥补统一理论法无法模拟施工过程、读取钢管初应力的不足，本文按统一理论双单元法的思路建立有限元模型。顾名思义，统一理论双单元法模型中拱肋钢管混凝土由钢管和管内混凝土两部分材料组成，在空钢管阶段，模型与刚度叠加双单元法保持一致，当拱肋主管管内混凝土灌注后形成强度时，激活管内混凝土单元，同时将钢管单元的截面特性值调整为按统一理论法计算的数值。实际上，该方法是统一理论法与刚度叠加法的混合应用。

2 两种规范刚度取值的比较

刚度叠加法和统一理论法分别对应于2013 规范和2015 规范，是目前最常用的两种方法。为比较两者在刚度取值上的差异，假设按2013 规范和2015 规范计算的轴向刚度、抗弯刚度依次为X（EA）、X（EI）和Y（EA）、Y（EI），相对误差Z=（Y-X）/X，目标误差，以钢管壁厚t 与混凝土强度等级为自变量，分别以相对误差Z 和目标误差K 为因变量，针对不同钢材壁厚和混凝土强度等级组成的钢管混凝土拱肋，探讨分析两种规范的计算方法对拱肋轴向刚度和抗弯刚度的影响。图1为钢管外径（1.2 m）和钢材牌号（Q345）相同时，混凝土强度等级分别为C50、C60、C70 对应的相对误差Z 和目标误差K 随钢管壁厚t 的变化曲线。需要说明的是，图1（a）中所有曲线在壁厚18 mm 处骤降，这是因为2015 规范针对钢管厚度大于16 mm 的组合结构，其弹性模量在查表取值的基础上考虑了修正系数0.96。

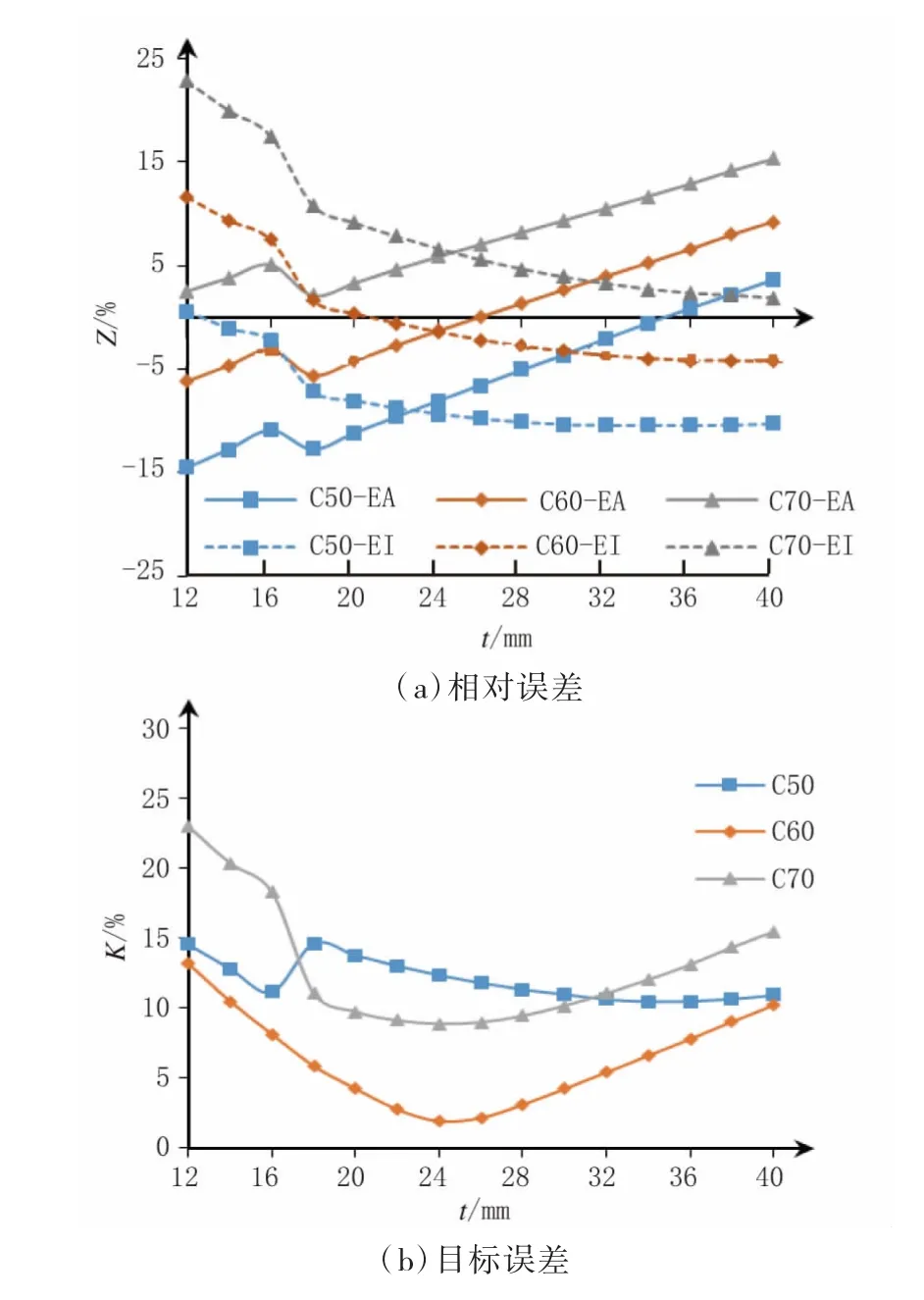
图1 不同钢管混凝土的相对误差和目标误差随壁厚的变化曲线

从图1（a）中可以看到，无论轴向刚度还是抗弯刚度，C60 的相对误差均处于C70 和C50 的包络中，且t＜36 mm 时，相对误差的大小关系为C70＞0＞C50；随着壁厚t 增大，轴向刚度对应的Z 值线性递增，而抗弯刚度对应的Z 值逐渐减小，最后趋于平缓。由此可知，当壁厚为12～34 mm 时，对于C50 钢管混凝土的轴向刚度和抗弯刚度计算值，刚度叠加法均大于统一理论法，而C70 钢管混凝土与之相反，C60 钢管混凝土按这两种方法计算的轴向刚度和抗弯刚度的大小关系并非一致，与钢管壁厚息息相关。

由图1（b）可知，C60 钢管混凝土的目标误差随着壁厚的增大先减小后增大，在壁厚为24 mm 时达极小值；此外，与C50、C70 钢管混凝土相比，C60 钢管混凝土对应的目标误差最小。侧面反映出对于外径1.2 m 的钢管混凝土，C60 混凝土与Q345 钢材的匹配性更优，且钢管壁厚为20～32 mm 时最佳，与根据文献[9]和文献[10]计算的壁厚取值范围相符合。

3 模拟方法对结构力学行为的影响

为探究拱肋不同模拟方法对钢管混凝土拱桥结构力学行为的影响，以净跨径390 m 中承式钢管混凝土拱桥为研究对象，分别按照刚度叠加法、统一理论法和统一理论双单元法等模拟方法，建立全桥三维空间有限元模型进行静力计算和稳定分析。在恒载作用下，探讨这三种模拟方法对主拱轴力、位移和稳定性等力学行为的影响。

3.1 桥梁简介

白马渠江特大桥主桥是镇巴至广安高速公路上一座计算跨径为418.8 m 中承式钢管混凝土有推力拱桥（见图2），主拱拱轴线采用悬链线线形，净跨径为390 m，矢高97.5 m，计算矢跨比为l/4，拱轴系数为1.65。主拱圈采用两片平行布设的四肢桁架拱肋，双片拱肋中距31 m，肋宽4 m，拱顶桁架高6.5 m，拱脚桁架高12.0 m。拱肋弦管采用Q345 钢材，外径为1.2 m，壁厚从拱顶至拱脚依次为22/26/30/34 mm，管内灌注C60 混凝土。桥面宽29.5 m，吊杆间距为14 m。双片拱肋之间采用“△+I”形式横撑。主梁采用格子钢梁叠合25 cm 混凝土的组合结构。两岸拱座均为钢筋混凝土拱座接扩大基础。桥梁标准横断面见图3。

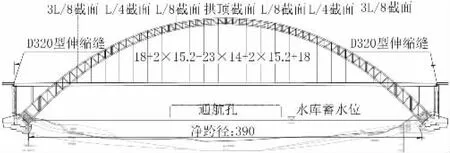
图2 白马渠江特大桥主桥立面布置（单位：m）

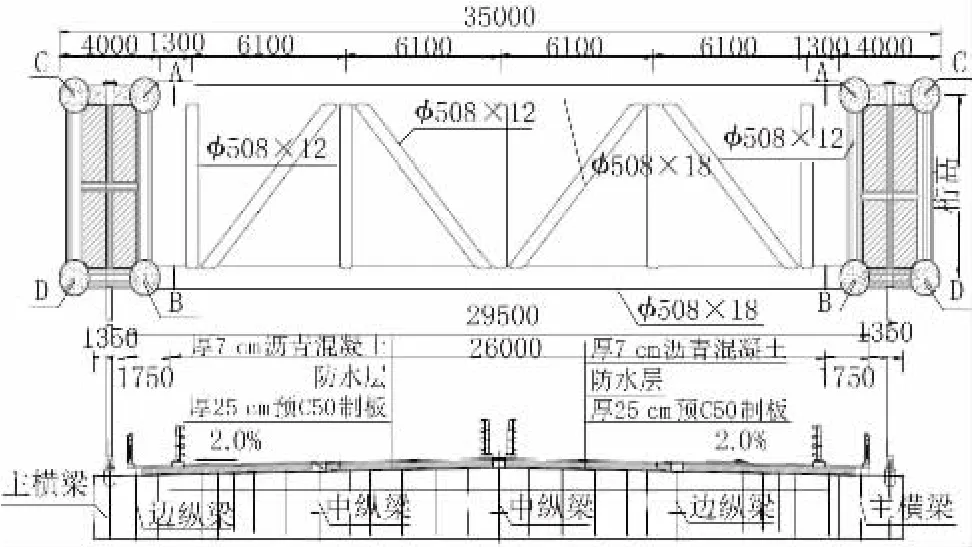
图3 白马渠江特大桥主桥标准横断面（单位：mm）

3.2 计算模型

以白马渠江特大桥为工程依托，分别按照刚度叠加法、统一理论法和统一理论双单元法等模拟方法，采用Midas Civil 依次建立全桥三维空间有限元模型，见图4。主梁、主拱横向连接系、纵横梁等各杆件采用空间梁单元，扣索和吊杆采用只受拉的索单元，拱脚加劲板和吊杆横隔钢板采用板单元模拟。

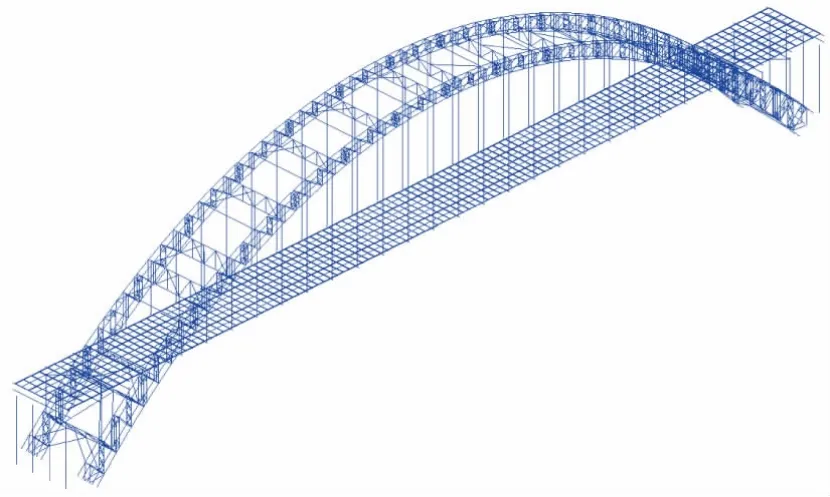
图4 全桥三维空间有限元模型

3.3 结构力学行为分析

由于拱脚截面采用了外包混凝土方案，传力途径不明确，且受力复杂、应力集中现象突出。因此，本文以拱肋的拱顶截面、L/8 截面、L/4 截面和3L/8 截面等四个关键截面（下文简称主拱四个关键截面）作为重点关注对象，关键截面位置见图2。探讨分析在成桥态恒载作用下，不同拱肋模拟方法对主拱轴力、变形和稳定性等力学行为的影响。

3.3.1 主拱轴力分析

钢管混凝土拱桥主拱受力以轴压为主，恒载效应占主导地位[12]，本文针对主拱在恒载作用下主拱四个关键截面的轴力受不同拱肋模拟方法的影响进行分析。设拱肋内肢和外肢的上、下弦管编号依次为A、B、C、D，见图3。为便于比较不同模拟方法对应的有限元计算结果，分别以统一理论法、统一理论双单元法与刚度叠加法的比值为依据进行探讨。

图5 给出了拱肋采用不同模拟方法时主拱四个关键截面的轴力比较。从图中可以看到，主拱四个关键截面采用统一理论法、统一理论双单元法的轴力计算结果与刚度叠加法相比，相对差值均不超过5%，且四肢主管在不同位置的相对差值存在变化；对于不同的拱肋模拟方法，主拱四个关键截面对应的轴力大小关系均保持一致，各弦管的轴力大小关系具体表现为：内肢上弦管A——刚度叠加法＞统一理论双单元法＞统一理论法；内肢下弦管B 和外肢上弦管C——统一理论双单元法＞刚度叠加法＞统一理论法；外肢下弦管D——统一理论法＞刚度叠加法＞统一理论双单元法。

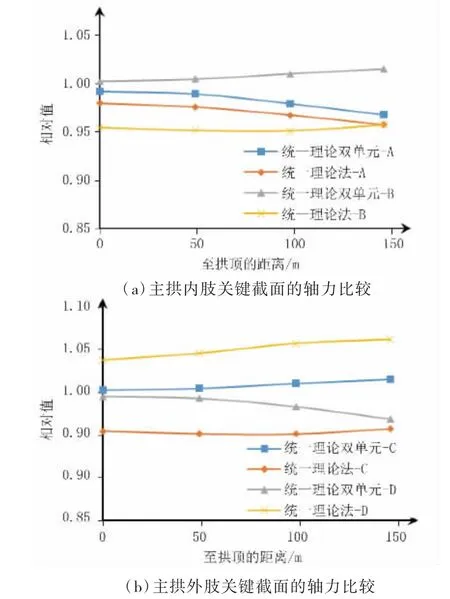
图5 拱肋采用不同模拟方法时关键截面的轴力比较

3.3.2 主拱位移分析

表2 为拱肋采用不同的模拟方法时主拱在恒载作用下4 个关键截面的竖向位移，其中CS1、CS2、CS3 分别对应于统一理论法、统一理论双单元法与刚度叠加法。

表2 主拱关键位置的竖向位移

由表2 可知，对于拱肋的竖向位移，统一理论法在主拱4 个关键截面的计算结果均小于刚度叠加法，而统一理论双单元法除3L/8 截面之外，其余3个关键截面的计算结果都大于刚度叠加法；相比统一理论双单元法，统一理论法在拱顶截面和L/8 截面的竖向位移计算结果与刚度叠加法更接近；此外，统一理论法和统一理论双单元法的竖向位移相对刚度叠加法的误差值从拱顶至3L/8 截面逐渐增大。由此说明，拱肋采用统一理论法模拟的整体刚度大于刚度叠加法，这两种模拟方法对应的主拱竖向位移的差异性从拱顶至3L/8 截面逐渐扩大。

3.3.3 桥梁稳定分析

图6 给出了拱肋分别采用统一理论法、统一理论双单元法与刚度叠加法等不同模拟方法时，主拱在恒载作用下的稳定系数随屈曲模态的变化关系。

图6 主拱屈曲系数随屈曲模态的变化曲线

从图6 可以看出，主拱分别采用统一理论法、统一理论双单元法和刚度叠加法进行模拟时，其稳定系数均大于5，且它们随不同屈曲模态的变化趋势基本一致；这三种模拟方法的稳定系数大小关系为：统一理论法＞统一理论双单元法＞刚度叠加法；相比刚度叠加法，统一理论双单元法在前5 阶的稳定系数与统一理论法更接近。显而易见，拱肋采用统一理论法和统一理论双单元法模拟的稳定性均高于刚度叠加法，这是因为这两种方法都考虑了钢管对核心混凝土的套箍作用，能够充分发挥钢混凝土材料各自的优点。

4 结 语

通过2013 规范和2015 规范针对钢管混凝土拱肋的刚度取值比较，结合统一理论法、统一理论双单元法与刚度叠加法等不同模拟方法对白马渠江特大桥在成桥态恒载作用下结构力学行为的探讨分析，主要得到以下一些结论：

（1）钢管混凝土拱肋的轴向刚度和抗弯刚度，按统一理论法和刚度叠加法计算的数值相对大小与混凝土强度等级和钢管壁厚有关，根据两种方法计算的刚度误差可检验钢管与混凝土的强度等级是否匹配。

（2）对于外径1.2 m 的钢管混凝土，C60 混凝土与Q345 钢材的匹配性更优，且钢管壁厚为20～32 mm 时最佳。

（3）主拱4 个关键截面采用统一理论法、统一理论双单元法的轴力计算结果与刚度叠加法相比，相对差值均不超过5%，3 种模拟方法对应的轴力大小关系在四肢弦管中存在异同，但沿各关键截面均保持一致。

（4）与刚度叠加法相比，统一理论双单元法在前5 阶的稳定系数与统一理论法更接近；统一理论法模拟拱肋的整体刚度和稳定系数均大于刚度叠加法，是分析大跨钢管混凝土拱桥稳定的一种可靠、经济的方法。