基于改进鱼群算法的UUV路径跟踪控制参数整定研究

杨 洋,王 征,周 帅,尹 洋

(海军工程大学, 武汉 430000)

0 引言

无人水下航行器(UUV)已经成为水下探测、海洋资源开发的重要工具之一,当下正服务于海洋军事、海洋经济等多个领域。由于UUV具有强非线性与强耦合性的动力学特性,以及水下环境的不确定性,其水下运动控制器的设计难以参照无人车、无人机等相对成熟的无人系统,已成为其他重要功能的基础瓶颈。

文献[1]结合模糊控制器与PD控制器的理念,设计了一种水下机器人的S面控制器,具有输入参数少、对水下系统拟合程度高、实用性强的特点,并在后续的多次外场试验中证明了有效性。文献[2]中使用收敛性较好的其他非线性函数替代S面控制器中的Sigmoid函数,形成了广义S面的水下机器人控制器,能取得更好的控制效果。但是传统S面控制器中的控制参数往往是固定的,不具备自适应能力,且需要人为设定并调整,这类近似方式使得UUV在水下运动过程中仍有较大的跟踪误差,不符合实际应用。因此将智能优化算法运用到控制参数的整定中成为了有效的解决途径[3-7]。

近年来已有部分学者研究了智能算法在S面控制器参数整定中的应用,包括粒子群算法[8-11]、神经网络[12-13]、模拟退火算法[14]等。而在众多优化算法中,人工鱼群算法由李晓磊于2002年提出[15],拥有全局寻优能力,具备收敛速度快、对不确定性模型拟合性较好的特点,适用于UUV路径跟踪控制这种较为复杂的非线性数学模型。但同样人工鱼群算法也存在一些问题,比如算法迭代后期具有盲目性,收敛速度减慢;后期一旦陷入局部最优值则难以跳出等。

针对人工鱼群算法存在的问题,提出一种改进的人工鱼群算法,改进措施包括:在人工鱼4种基础行为中加入夺食行为、在鱼群移动时使用自适应步长、在觅食行为时使用带衰减因子的视野范围,提高了人工鱼群的优化性能。为避免人为设定无人水下航行器控制参数带来水平面路径跟踪误差较高的问题,并使用上述改进算法优化整定UUV水平面路径跟踪任务的前向速度控制器与艏向控制器的控制参数。经过仿真分析与水下实物试验,验证了改进鱼群算法在UUV路径跟踪控制器参数整定中的可行性与有效性。

1 基于S面控制器的路径跟踪控制

UUV在执行多数水下任务时常需保持定深航行,故本文中UUV路径跟踪控制考虑在水平面中,UUV控制前向速度的推进器推力控制器与控制艏向的垂直舵机角度控制器,将其路径跟踪控制分解为上述两个控制器分别设计。

在为UUV路径跟踪设计模糊控制器时,往往采用两边疏松中间密集的方式,即在偏差e较大时控制较为粗糙,e变小时控制逐渐精细。当模糊控制表的分辨率趋近于无穷小时,无数小折面便可简化为光滑曲面,而Sigmoid曲面的变化趋势与这个设计思想类似,如图1所示。

图1 Sigmoid曲面示意图Fig.1 Sigmoid plane diagram

因此,可以使用Sigmoid曲面代替此类模糊控制的规则表,形成S面控制律[1]。在使用传统S面控制器的过程中,常常存在前向阻尼带来的稳态误差无法消除的问题,故在Sigmoid函数的指数项中引入积分控制以消除该类稳态误差,如式(1)所示。

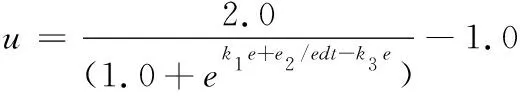
(1)

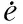
在水下复杂的环境中,海流等未知的干扰因素可以简化为一定时间之内施加于UUV的固定干扰力,在式(1) 的基础上加入Δu项以增量输出抵消此类稳态误差,表达式如下:

(2)

通过上述方式可构造UUV完成路径跟踪任务所需的推力控制器与艏向控制器,但其中控制参数k1-k3的选定往往靠经验丰富的人员手工完成,在工程实际中带来了较大的困难,故可使用智能优化算法如人工鱼群算法实现控制参数的自整定。

2 人工鱼群算法及其改进

2.1 经典人工鱼群算法

在一片水域中,鱼往往能自行或尾随其他鱼找到食物多的地方,因而鱼生存数目最多的地方一般就是本水域中食物浓度最高的地方,人工鱼群算法就是根据这一特点,通过构造人工鱼来模仿自然鱼的多种生存行为,实现寻优。

人工鱼拥有以下几种典型行为,其中各行为的经典数学表达参见文献[15]:

1) 觅食行为:一般情况下鱼在水中随机地自由游动,当发现食物时,则会向食物浓度升高的方向快速游去。

2) 聚群行为:由于趋利避害的天性,鱼在游动过程中为了更大的生存可能性和躲避天敌会形成集群。

3) 追尾行为:当鱼群中的一条或几条鱼发现食物时,其临近的伙伴会尾随其快速到达食物点。

4) 随机行为:单独的鱼在水中通常都是随机游动的,这是为了更大范围地寻找食物点或身边的伙伴。

人工鱼对外界环境的感知是依靠其视觉实现的,人工鱼的模型中使用如图2所示的方法实现人工鱼的虚拟视觉。

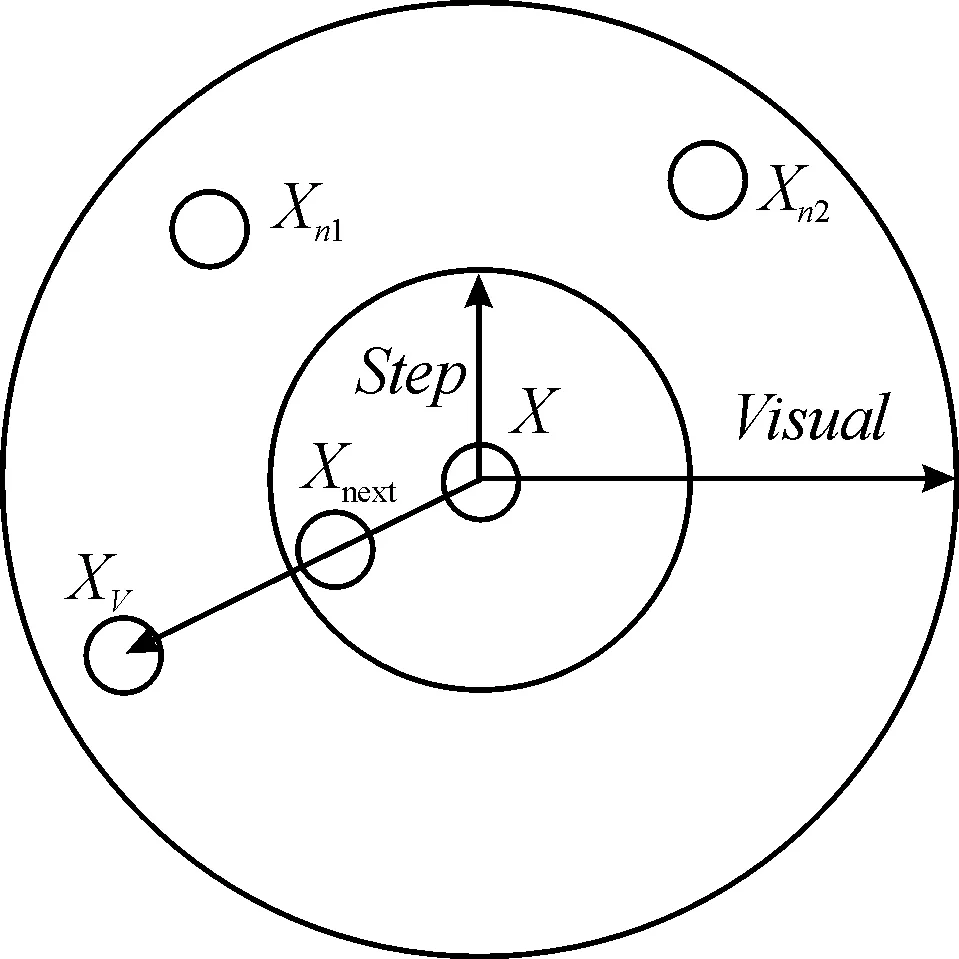
图2 人工鱼视觉概念图Fig.2 Artificial fish visual concept map

图2中X表示人工鱼当前位置,Step表示移动的步长,Visual表示视觉范围,如果XV位置食物浓度高于当前位置浓度,则向其方向前进至Xnext位置,XV和Xnext与X的关系可用式(3)—式(4)分别表示:

XV=X+Visual*r

(3)

(4)

其中,r为[-1,1]区间的随机数。

2.2 改进措施

针对经典鱼群算法存在的部分问题,使用以下策略进行改进。

1) 自适应步长

人工鱼在向食物浓度高的地方游动时,选取该方向上随机位置,若当前位置距离食物浓度最高处较近时将在最优值附近振荡,易导致算法耗时较长,这也是算法迭代后期收敛速度减慢的主要原因。针对这一问题,可考虑采用自适应步长的方式进行改进,即当前位置距离食物浓度更高处较近时应使用较小的Step值,具体数学表述如下:

(5)

式(5)中:Xi表示人工鱼当前位置;XV表示其视野范围内某一位置,当XV处食物浓度值大于当前位置浓度时,则该人工鱼向其方向上游动Step距离。因当前位置距离食物浓度更高处较近时使用了更小的Step值,则当附近存在局部最优值时会因收敛过快而陷入其局部最优而难以跳出,故加入Rand()函数的以提供随机性,便于跳出。如果人工鱼执行完聚群追尾行为之后没有移动到食物浓度较高处,同样为了增大随机性跳出局部最优值,Step将仍使用固定值。

2) 带衰减因子的视野范围

鱼群的觅食行为在解决离散型优化问题时具有相当重要的地位。鱼群在觅食时,视野保持不变,当人工鱼逐渐接近最优解时,其状态Xi仅有1～2个维度不同于最优解,此时仍然使用原来固定的Visual值将导致人工鱼盲目寻优,大幅增加了算法迭代后期的复杂性。同时,若采用固定的Visual值,过大的视野范围会导致过慢的收敛速度,过小的视野范围将加大陷入局部最优值的可能性。为了避免这一缺陷,可采用下述策略改进觅食行为:

当算法开始迭代时,使用较大的Visual值扩大寻优范围。随着迭代过程的进行,逐步适当减小Visual值以加快收敛速度。数学表达为

Visuali=αVisuali-1

(6)

式(6)中:α∈(0,1)表示视野范围的衰减速率;i表示迭代次数。

3) 夺食行为

真实自然界中,当周围食物浓度低到一定程度时,鱼会因饥饿产生攻击性。如果视野范围内有其他鱼占据着较多的食物时,饥饿的鱼会试图夺取食物较多的鱼的位置,称之为夺食行为。因此可以考虑将夺食行为加入人工鱼的基本行为之中。具体数学表述如下:

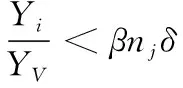
(7)

式(7)中:Yi表示当前位置Xi的食物浓度,当其与视野范围中某一位置XV的食物浓度YV的比值小于某一值时,则该人工鱼执行夺食行为。这一阈值用执行可能性β=rand(0,1)与拥挤度因子的乘积表示。

加入夺食行为的目的在于加强了人工鱼群向目标函数更优值聚集的趋势,同时引入随机性,更利于跳出局部最优值。

改进人工鱼群算法的流程如图3所示。

图3中,人工鱼每选择一次当前执行的行为,都将使用当前坐标计算食物浓度值判断是否更优,计算过程是完成一次路径跟踪任务取得指标值。该环节是改进鱼群算法的主要环节。

图3 改进鱼群算法流程图Fig.3 Flow chart of improved fish swarm algorithm

3 基于改进鱼群算法的S面路径跟踪控制

UUV路径跟踪控制主要包括前向速度控制器与艏向控制器。前向速度控制器通过控制推进器转速以跟踪期望前向速度,艏向控制器通过控制艉部垂直舵的舵机角度以跟踪期望艏向。

前向速度控制器设计如下:

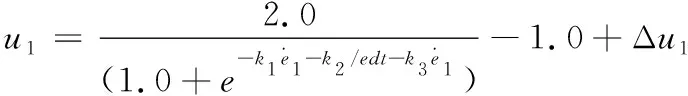
(8)

e1=vb-v

(9)

式(9)中:vb为前向速度期望值;v为UUV当前速度。

由于艏向控制中不存在前向阻尼带来的稳态误差,故将积分项系数设置为零,其控制器设计如下:

(10)

e2=ψb-(ψ+β)

(11)

式(11)中:ψb为大地坐标系下UUV期望艏向;ψ为UUV实际艏向;β为漂角。

上述2个S面控制器中需要优化的参数包含k1、k2、k3、k4、k5五个。由于UUV在水下运动时动力学模型具有强耦合性与非线性的特点,前向速度与艏向输出之间的耦合无法解耦,故在使用改进鱼群算法进行控制参数的优化时将人工鱼的位置坐标设置为四维向量(k1,k2,k3,k4,k5)。选取2个S面控制器中偏差绝对值乘以时间项对时间的积分之和作为算法的目标函数,既能体现出误差的大小(控制精度),又能体现误差收敛的速度,兼顾了控制精度和收敛速度,反映了控制系统的控制准确度及快速程度,其值越小,则控制器效果越好,目标函数使用式(12)表达。

(12)

值得注意的是,经典人工鱼群算法描述中,人工鱼的最终目的是寻得食物浓度最高值,但在UUV水平面路径跟踪控制任务中,需要求得使控制器指标最小时的控制参数值,即寻求人工鱼(k1,k2,k3,k4,k5)的食物浓度值最低处,原理相同,仅描述上存在差异。

最终经过指定次数的迭代,产生使控制器指标值最小时的控制参数K1、K2、K3、K4、K5值,以此作为优化整定后的控制器参数,代回两个控制器中,即可完成UUV水平面路径跟踪控制任务。

4 仿真与试验分析

围绕上述的理论分析,进行了基于改进鱼群算法的UUV水平面路径跟踪控制的代码仿真,并将其与经典人工鱼群算法优化S面控制器参数的相同算例进行对比,比较得出改进鱼群算法在UUV水平面路径跟踪控制参数的优化整定中的应用具有可行性与优越性。仿真平台为Matlab R2017a软件,个人电脑系统为Windows 7,运行内存12GB,CPU为Intel i7-4710MQ。仿真中使用的人工鱼群各参数值如表1所示。

表1 改进鱼群算法参数选定

改进鱼群算法与经典鱼群算法在迭代过程中的控制器指标Y值变化如图4所示。

图4 改进鱼群算法与经典鱼群算法指标值变化对比图Fig.4 The comparison chart of the index value change between the improved fish swarm algorithm and the classic fish swarm algorithm

从图4中可以看出,经典鱼群算法在迭代10～40次范围时收敛速度明显慢于改进后的鱼群算法,迭代40次后指标值在334附近停滞,难以跳出该局部最优值,后期无法达到目标函数最优值处。而经过前述3个措施,改进的人工鱼群算法在迭代中期的收敛速度有所提高,且在迭代60次后跳出局部最优值,将指标值优化至321.4,验证了改进鱼群算法的优越性。

完整迭代MAXGEN次之后,改进鱼群算法输出控制器指标Y最小时的控制参数值(保留两位小数)如表2所示。

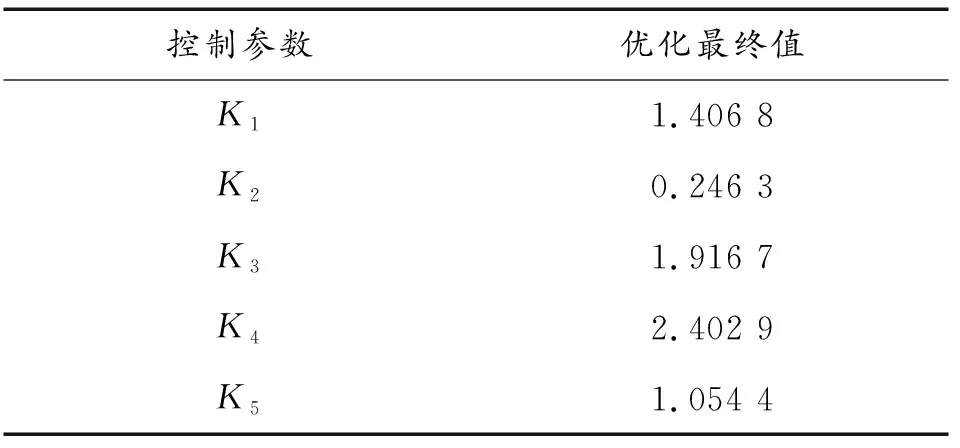
表2 优化整定后的控制参数值

将上述控制参数代回S面前向速度控制器与艏向控制器中,执行UUV水平面的路径跟踪任务,将得到的规划路径与跟踪轨迹图与相同条件下整定前的跟踪轨迹图对比如图5所示。

图5中,整定前通过人工试凑参数的控制器指标值Y=8 062.7,整定后的指标Y=321.4,经过整定使式(12)表达的指标值降低96%,意味着整定后的控制器具有更高的控制精度与收敛速度。明显地,整定后的路径跟踪控制器的性能更好。同时经过参数整定前后的水平面路径跟踪轨迹图对比可以发现,经过改进鱼群算法的优化,UUV在进行水平面路径跟踪时的振荡明显减少,跟踪误差显著降低,验证了改进鱼群算法在UUV的S面路径跟踪控制参数整定中应用的合理性与可行性。

图5 控制参数整定前后的路径跟踪轨迹对比Fig.5 Comparison of path following track before and after control parameters tuning

为验证本算法在工程实际中的有效性,选在天津塘沽炮台附近水域进行了基于S面控制器的UUV的水平面路径跟踪外场试验。与上述仿真类似,经过改进鱼群算法优化得出适用于彼时彼地的控制参数值,将此参数载入UUV中完成水平面路径跟踪试验。为避免环境与人为动作带来的偶然误差,相同的路径跟踪试验进行了3次。试验完成后读取数据绘制航线如图6所示。

图6 基于S面控制器的UUV水平面路径跟踪试验轨迹Fig.6 Experimental track of UUV plane path following based on S plane controller

从图6中可以看出,经过改进鱼群算法优化整定后的控制参数可以使S面控制器较好地完成UUV水平面路径跟踪任务,UUV顺利地从起始点出发沿着规划路径到达预设终点,并保持较小的路径偏差,验证了改进鱼群算法在UUV水平面路径跟踪控制参数优化整定中的可行性与有效性。

5 结论

1) 对于UUV的前向速度控制器,在传统S面控制器的指数中引入积分项,消除了稳态误差。

2) 改进经典人工鱼群算法,经过夺食行为、自适应步长、带衰减因子的视野范围等方法的改进,算法在迭代中后期的收敛速度加快,后期跳出局部最优值的能力增强。

3) 使用改进鱼群算法对UUV水平面路径跟踪控制器的五个控制参数进行优化整定。经过整定使控制器的指标值降低了96%,大幅减小了UUV的跟踪偏差,提高了控制器的控制精度与收敛速度。

4) 经过仿真与实物试验的验证,所完成的基于改进鱼群算法的UUV路径跟踪控制参数整定研究可投入工程使用,完善当前UUV运动控制领域的不足。