威胁环境下四旋翼的轨迹规划与跟踪控制研究
何信弟,赵超轮,戴邵武,郑百东
(1.中国人民解放军第4801工厂虎门军械修理厂, 广东 东莞 523938; 2.海军航空大学, 山东 烟台 264000)
0 引言
低空突防任务是无人机在战场中的重要任务之一,它是一个多变量、多约束、多目标的复杂问题,直接处理起来难度较大。可按照分层递阶结构的思想将这一问题分解为轨迹规划与跟踪控制等2个子问题,从而简化问题的求解难度。
无人机轨迹规划问题可以抽象为在包含微分方程、代数方程和不等式等约束下求解泛函极值的开环最优控制问题[1]。对于最优控制方法,按照求解策略的不同,可以分为直接法和间接法。其中直接法的应用更为广泛,其思路是先采用参数化方法将连续最优控制问题转化为非线性规划问题(nonlinear programming problem,NLP),然后利用非线性优化算法求解最优轨迹[2-4]。伪谱法是直接法中的一类典型代表,因其对初值不敏感、收敛速度快、求解精度高等优点已被广泛应用于无人机轨迹规划、导弹制导、航天器轨道机动等最优控制问题。目前发展较为完善的伪谱法包括Gauss伪谱法、Legendre伪谱法、Radau伪谱法。上述方法的主要区别是配置点不同,以及与此对应的估计多项式不同[5-8]。刘鹤鸣等[9]以雷达威胁概率最小和攻击时间最短为目标,在考虑动态雷达散射截面的情况下,利用可变低阶自适应伪谱法实现了固定翼无人机的轨迹规划。徐建龙等[10]以轨迹最短为目标,在考虑静态障碍的情况下,利用hp自适应Radau伪谱法实现了四旋翼无人机的轨迹优化。宋晓晨等[11]以最小油耗和最小时间为目标,利用hp自适应伪谱法求解超音速无人机的轨迹最优化问题。虽然伪谱法能够较好地处理轨迹规划问题,但是该方法一般只能离线使用,且只能应对已知威胁。
无人机轨迹跟踪控制方法有很多,应用最广泛的是PID控制,此外还有滑模控制、反步控制、模型预测控制(model predictive control,MPC)等。其中模型预测控制具有显式处理约束、反馈校正、滚动优化等特点,其应对不确定环境的能力更强[12]。因此,在具有未知障碍等威胁的环境中,MPC方法具有显著的优势。Yeonsik Kang等[13]在二维平面内,利用固定翼无人机的运动学模型设计了非线性MPC控制器,通过在目标函数中引入避障惩罚代价,实现了无人机与静态障碍物间的避碰。王怿等[14]在三维空间内,针对固定翼无人机设计了非线性MPC控制器,在避免无人机与未知静态及动态障碍物发生碰撞的情况下,实现了无人机沿参考轨迹飞行。其避障惩罚代价是在文献[13]基础上改进的,文中考虑了障碍物的大小,使得无人机能够及时避开大型障碍物,且文中采用了条件触发式避障,即当未知障碍与无人机的最小距离小于给定阈值时,才在目标函数中加入避障惩罚代价。但是在每次求解MPC优化问题时,文中将移动障碍物暂且视作了静止障碍物。这种设计虽然简便,但是不足以应对快速移动的障碍物。
虽然针对无人机轨迹规划、跟踪控制2个子问题各自的研究成果很多,但是要实现一个具体的任务,往往需要将2个问题及对应的方法综合统筹考虑。如何将2个问题有效衔接、2种方法取长补短以实现整体效益的最大化,仍是一个较为开放且值得研究的问题。考虑到无人机平台任务载荷性能有限、战场环境中已知威胁和未知威胁并存的实际情况,为了充分利用现有资源、有效保证任务实时性,采用离线与在线相结合的工作方式是较为合适的选择。
根据以上分析,以无人机执行低空突防任务为背景,以四旋翼为控制对象,在考虑低空雷达、动态障碍威胁的情况下,以无人机能够在最短时间内穿过威胁环境并到达指定位置为控制目标,将这一问题分解为离线轨迹规划与轨迹跟踪控制2个子问题来统筹处理。本文中所作的工作主要包括:
1) 针对离线轨迹规划问题,在已知四旋翼初始状态、目标状态、雷达信息的前提下,建立简化的四旋翼动力学模型、雷达威胁模型,考虑四旋翼平台性能等约束,采用hp自适应Radau伪谱法离线规划出一条任务时间最短、被毁伤概率最小的可飞轨迹。
2) 针对轨迹跟踪控制问题,以离线轨迹规划阶段得到的轨迹为参考轨迹,基于模型预测控制设计跟踪控制器,在目标函数中引入避障惩罚代价,使四旋翼在跟踪参考轨迹的同时,完成在线避障。其中避障惩罚代价采用了条件触发式设计,并且在每次求解优化问题时考虑了移动障碍物的预测位置。
1 离线轨迹规划
在离线轨迹规划阶段,仅考虑已知威胁。假设敌方雷达是主要威胁,雷达中心位于地面,其探测区域近似为半球,且我方已预知雷达位置及探测半径。这里采用hp自适应Radau伪谱法设计轨迹规划器,设计过程如下。
1.1 数学模型
离线轨迹规划问题一般可抽象为有限时间内的最优控制问题。即求解控制输入U(t),使Bolza型性能指标函数(式(1))最小[15],即:
J(X(t),U(t))=Φ(X(t0),t0,X(tf),tf)+
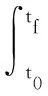
(1)
且满足状态方程

(2)
边界条件
Ψ(X(t0),t0,X(tf),tf)=0
(3)
路径约束
C[X(t),U(t),t]≤0,t∈[t0,tf]
(4)
以下是具体的建模过程。
1.1.1四旋翼模型
以“X字型”四旋翼无人机作为研究对象,如图1所示。建立2个右手坐标系,即惯性北东地坐标系与机体坐标系,如图2所示。其中,惯性坐标系odxdydzd以地面上任意一点为坐标原点od,odxd轴指向地理北,odzd轴垂直地面向下;机体坐标系obxbybzb与四旋翼机体固连,以机体重心位置为坐标原点ob,obxb轴在飞机对称平面内指向机头方向;obzb轴在机体对称平面内,垂直于obxb轴向下。
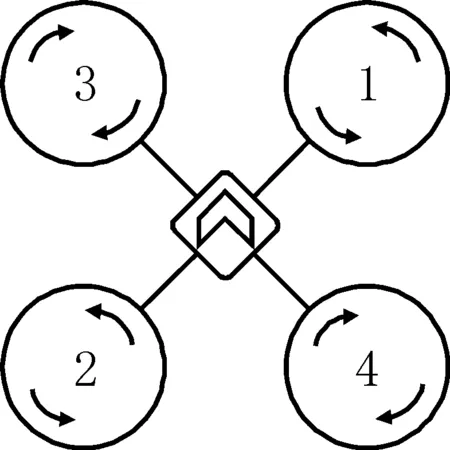
图1 X字型四旋翼Fig.1 X-shaped quadrotor

图2 惯性坐标系与机体坐标系Fig.2 Inertial coordinate system and body coordinate system
有关四旋翼无人机运动学、动力学建模的详细介绍可参考文献[16]。针对四旋翼轨迹规划问题,采用简化的数学模型,假设无人机拉力约等于重力,滚转角、俯仰角都非常小,可得到高度通道与水平通道解耦的模型为:
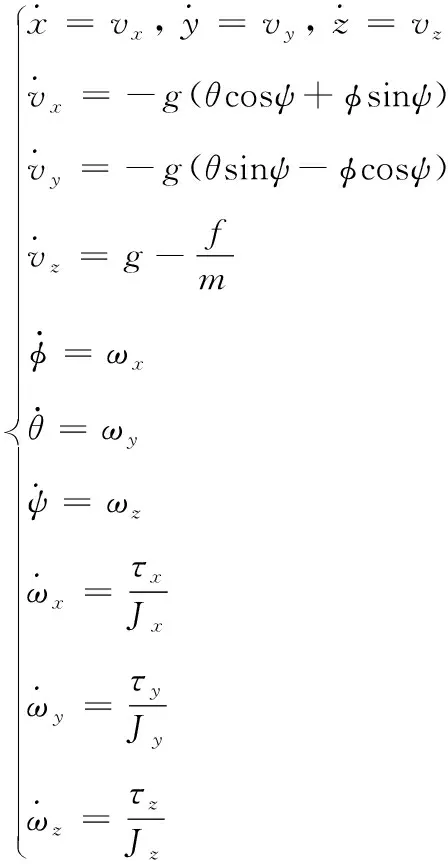
(5)
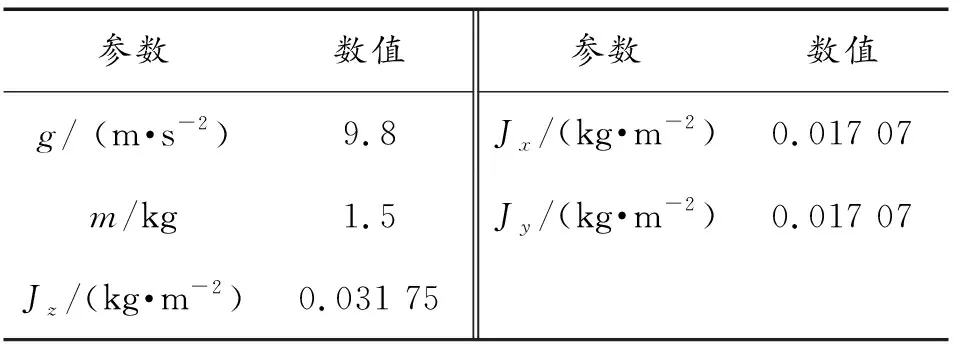
式(5)中:(x,y,z)、(vx,vy,vz)分别为无人机在惯性坐标系下的位置和速度,单位分别为m和m/s; (φ,θ,ψ)、(ωx,ωy,ωz)分别为无人机在惯性坐标系下的姿态和旋转角速度,单位分别为rad和rad/s;f为拉力;(τx,τy,τz)分别为滚转、俯仰、偏航力矩,(Jx,Jy,Jz)为3个轴的转动惯量;m为无人机质量;g为重力加速度。
选取状态量、控制输入量为:
X=(x,y,z,vx,vy,vz,φ,θ,ψ,ωx,ωy,ωz)T
(6)
U=(f,τx,τy,τz)T
(7)
1.1.2边界条件及路径约束
边界条件包括无人机状态量的初始条件与末端条件;路径约束包括无人机运动过程中需满足的状态约束、控制输入约束。具体如下:
1) 边界条件。
初始条件:X(t0)=X0,末端条件:X(tf)=Xf,其中,t0为初始时刻,tf为末端时刻。
2) 路径约束。

(8)
其中,位置约束体现了对无人机运动区域范围的限制,速度、姿态、角速度、拉力、力矩约束主要体现了平台自身性能的局限性。
注:轨迹规划时既需要考虑无人机自身性能约束,也需要考虑轨迹跟踪时的实际效果。需注意轨迹规划时所采用的速度最大值应小于跟踪控制时的速度最大值,否则可能会出现跟踪静差。
1.1.3目标函数
对于无人机执行低空突防任务而言,无人机的生存能力是遂行任务的基础,它决定了无人机能否安全抵达指定位置。此外,由于战场局势瞬息万变,攻击的时效性往往决定了任务能否顺利完成。因此,轨迹规划阶段包含2个目标:一是任务时间最短,二是被毁伤的概率最小。所设计的目标函数为:

(9)
式(9)中:w1、w2为权重系数;P(X(t))表示t时刻无人机被毁伤的概率。
无人机在执行任务过程中一般会受到地形因素、防空火力、雷达探测等威胁,其中雷达探测威胁是影响无人机生存能力的重要因素。在轨迹规划阶段,这里将无人机被雷达探测到的概率近似为其被毁伤的概率。无人机在t时刻的雷达探测概率模型可近似为[17]:
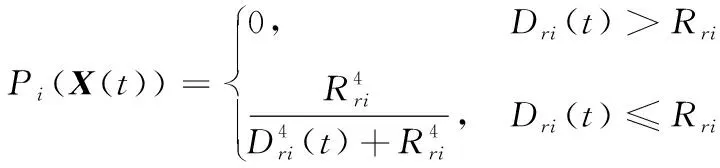
(10)
对于由Nra个雷达构成的联合防空系统,无人机瞬时被探测到的概率为:
1.2 基于hp自适应Radau伪谱法的轨迹规划算法
hp自适应Radau伪谱法是Radau伪谱法的hp自适应版本。Radau伪谱法采用Legendre-Gauss-Radau(LGR)配置点,“hp自适应”综合了增阶(p方法)和优化网格数目(h方法)2个方面的优势,能够根据网格的曲率和约束方程的误差自动地调整网格的数量和多项式的阶,因此其能够以较低的计算成本来提高算法的精度[9]。
hp自适应Radau伪谱法的一般步骤可参见文献[18]。可借助GPOPSⅡ软件求解该非线性规划问题。
由于通过上述伪谱法所得轨迹离散点的时间间隔并不均匀,而轨迹跟踪阶段所需的参考轨迹一般要求是均匀的,因此需要对所得轨迹的离散点进行均匀采样、插值处理,这里采用线性插值方法。
2 轨迹跟踪控制
在轨迹跟踪控制阶段,考虑预先未知的动态障碍物威胁。假设障碍物为球体,当障碍物进入无人机的探测范围后,无人机能够依靠机载探测设备实时获取障碍物的大小、位置及速度。这里采用模型预测控制设计跟踪控制器,设计过程如下。
2.1 数学模型
模型预测控制通常只取有限时域进行优化。在采样时刻k,从系统当前状态x(k|k)出发求解预测时域长度为N的优化问题,可表示为求解最优控制输入序列u(k+l|k), 0≤l≤N-1使目标函数(式(12))最小,即:

(12)
且满足:对于l=1,…,N-1,
状态方程约束:
x(k+l+1|k)=f(x(k+l|k),u(k+l|k))
(13)
状态、输入约束:
x(k+l|k)∈X,u(k+l|k)∈U
(14)
初值约束:
x(k|k)=x(k)
(15)
注:目标函数(12)一般是系统状态与输入的函数,应根据任务需求进行相应的设计。本文中目标函数的具体设计见第2.1.3节。
2.1.1四旋翼模型
假设四旋翼无人机配备自动驾驶仪,能够自动实现速度控制,即把速度指令输入给自动驾驶仪后,它能够自动控制四旋翼跟踪给定的速度指令。基于此,无人机的运动模型可以近似描述为如下连续时间线性时不变形式[19],有:
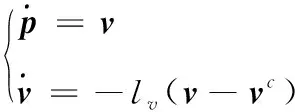
(16)


(17)
式(17)的离散化描述为:
x(k+1)=Gx(k)+Hu(k)
(18)
2.1.2约束
状态约束:

(19)
输入约束:

(20)
2.1.3目标函数
跟踪控制阶段要求无人机能够在避障的前提下,跟踪参考轨迹。因此,目标函数设计为:
J(k)=Jtra(k)+JΔu(k)+Jobs(k)
(21)
式(21)中:Jtra(k)表示跟踪参考轨迹的代价;JΔu(k)表示控制输入增量代价,它可保证无人机的速度不会剧烈变化;Jobs(k)为避障惩罚代价。式(21)中前2项的具体形式如下:
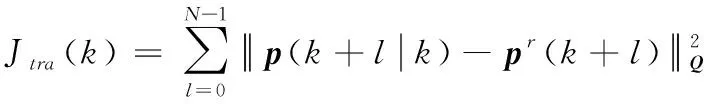
(22)
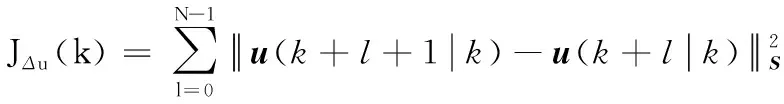
(23)

考虑到无人机计算资源有限,且障碍物的存在不一定会给无人机带来威胁,只有当障碍物与无人机的距离较近时,才有避障的需要。因此,采用条件触发式避障。在给出避障惩罚代价的具体形式之前,首先引入与四旋翼避障有关的几个半径,如图3所示。

图3 与避障相关的几个半径Fig.3 Several radii related to obstacle avoidance
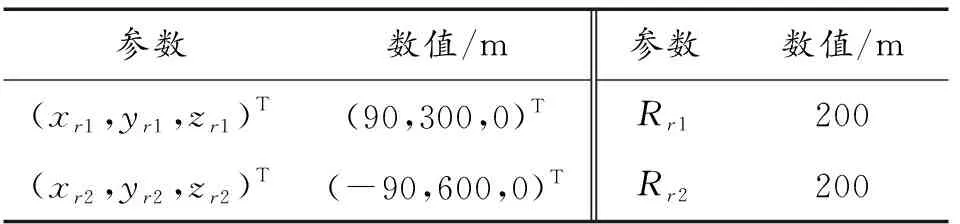
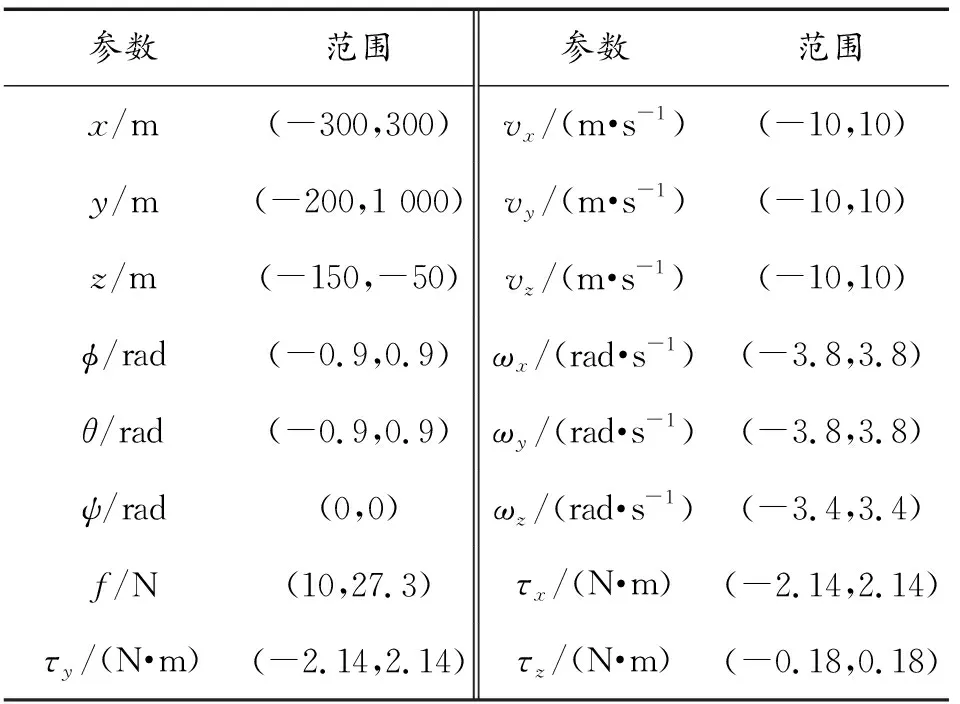
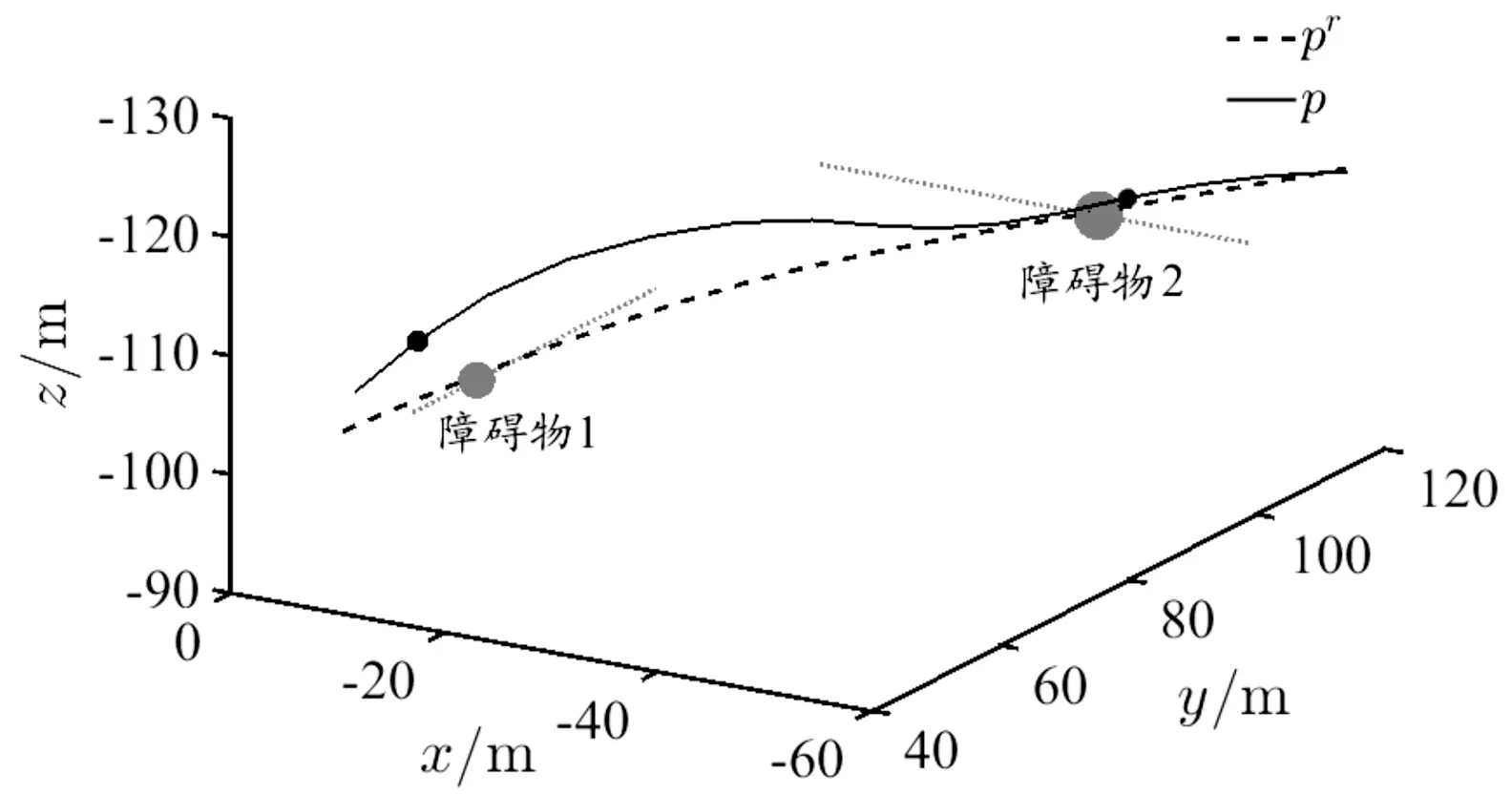
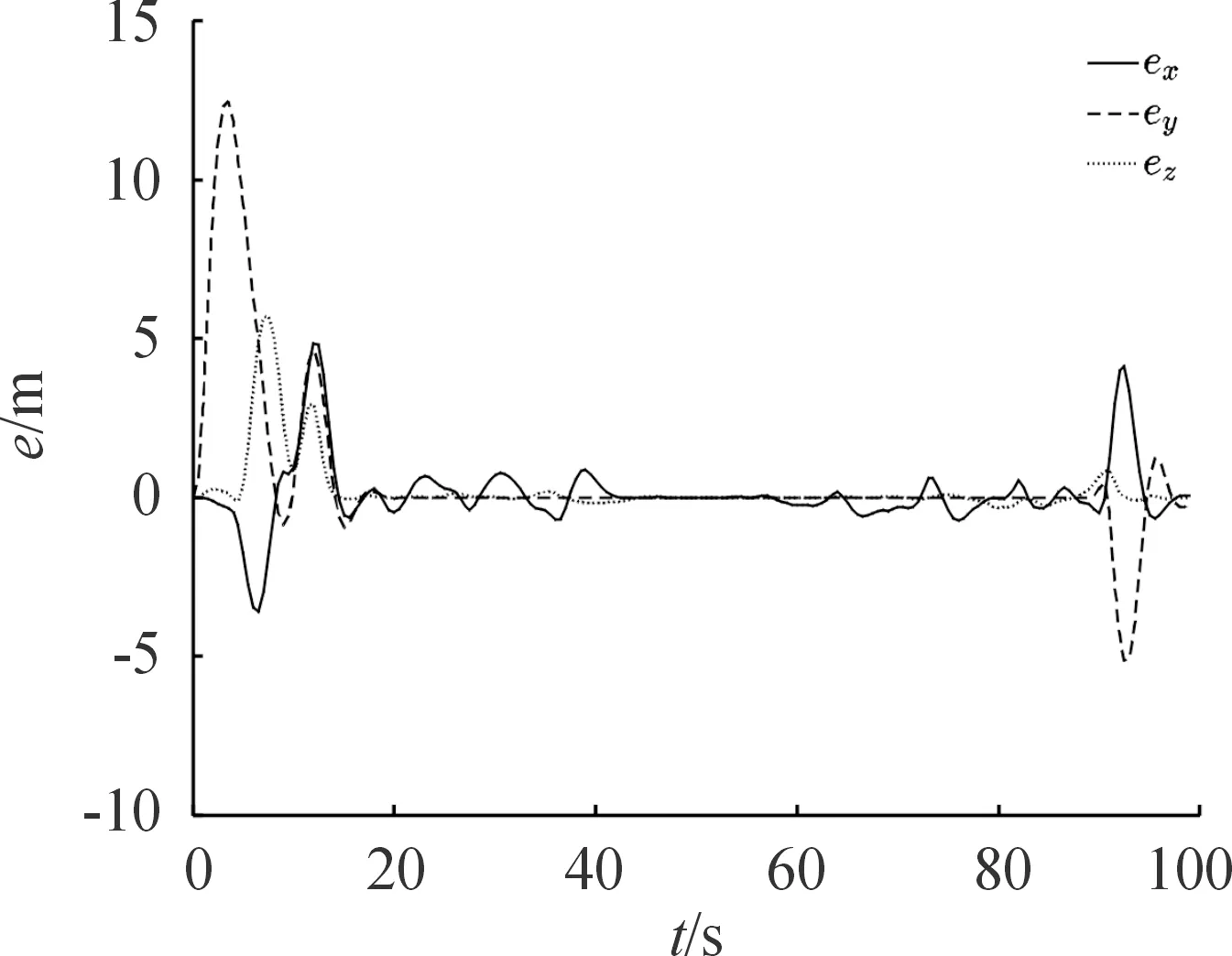
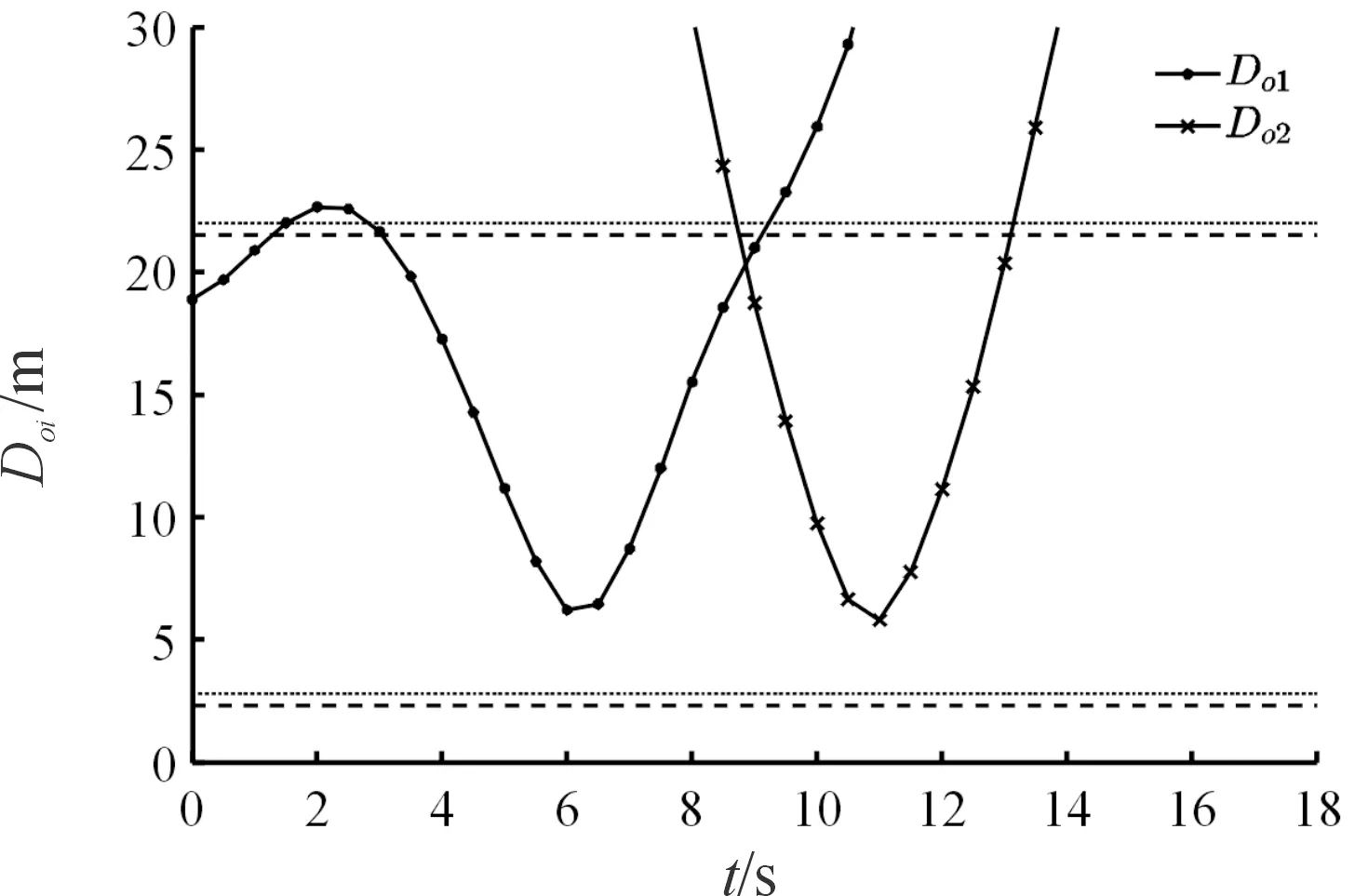
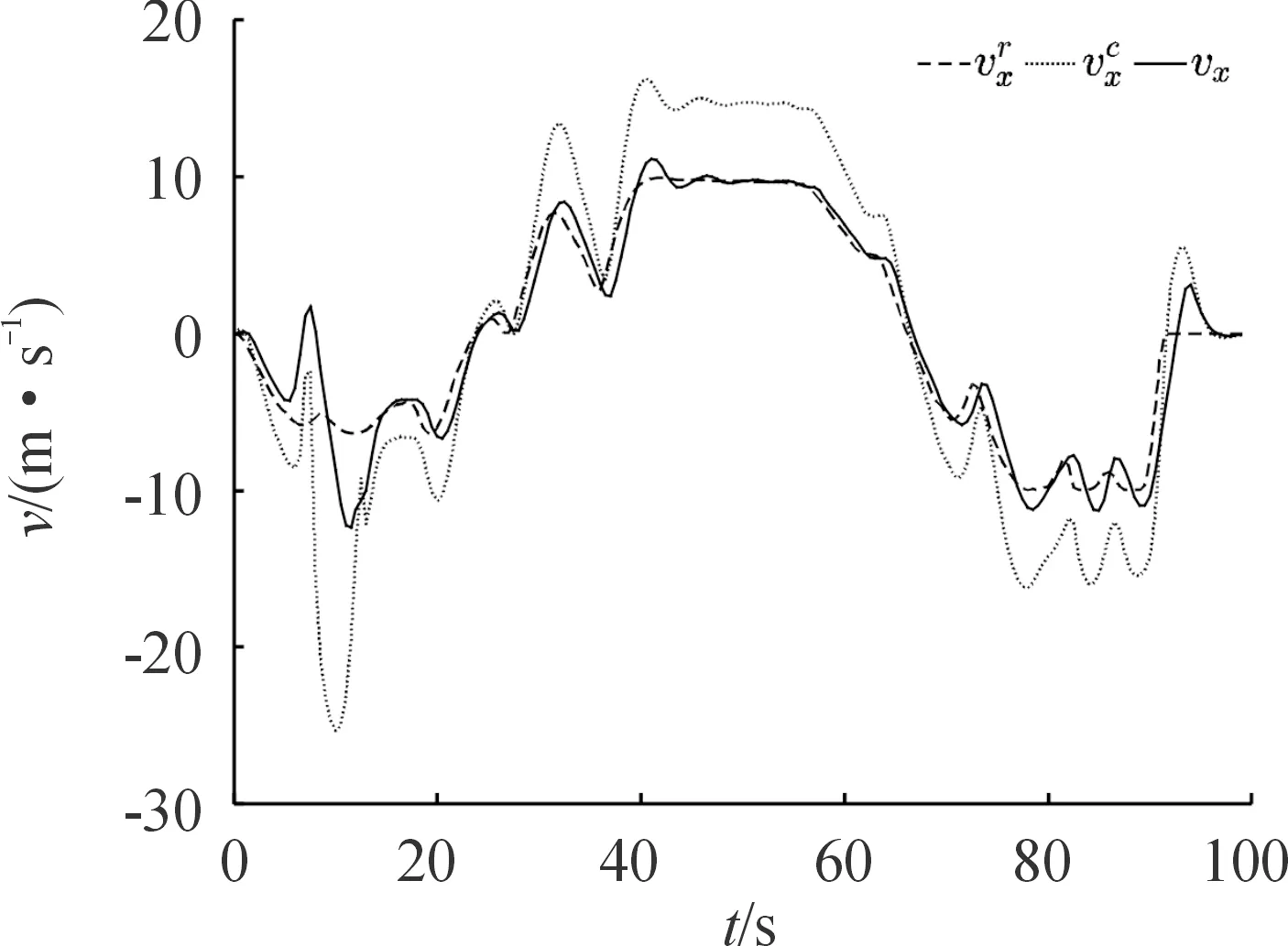
假设有Nobs个障碍物,用i表示障碍物的编号,i=1,2,…,Nobs。Roi为障碍物i的半径。以四旋翼几何中心为球心的3个半径的关系为Rs 基于以上分析,设计避障惩罚代价为: (24) 式(24)中, (25) 式(25)中, 令poi(k+l|k)=poi(k)+voi(k)·Ts·l表示k时刻预测的k+l时刻障碍物i的位置,Ts为采样时间,poi(k)、voi(k)分别为k时刻探测得到的障碍物位置和速度。注意k时刻的实际距离Doi(k)=Doi(k|k)。λ、σ为大于0的常数。 如式(25)所示,在k时刻,若当前时刻无人机与障碍物间的距离Doi(k)≤Ra+Roi,则Jm(k)>0,即触发避障功能。式(26)表征当无人机与障碍物间的预测距离Doi(k+l|k)较远,即未碰撞时,两者间的预测距离越小,避障代价越大;当两者间的预测距离小到已发生碰撞时,避障代价取一个较大的常值。 注3:区别于文献[14],式(26)中Doi(k+l|k)考虑了障碍物的预测位置poi(k+l|k),即使障碍物移动速度较快,应用该方法仍能有较好的避障效果。这里在预测障碍物的位置变化时,采用了匀速假设,这一预测方法较为简单,适用于障碍物速度不变或者变化较慢的情形。对于速度变化较快的障碍物,应采用更加符合目标运动特性的状态模型以及状态估计算法。 通过上述分析与建模,在采样时刻k,无人机从x(k|k)出发求解预测时域长度为N的优化问题,可表示为: (27) 对于l=1,…,N-1, s.t.x(k+l+1|k)=Gx(k+l|k)+Hu(k+l|k), x(k+l|k)∈X,u(k+l|k)∈U, x(k|k)=x(k) 具体算法步骤如下: 步骤1:在k时刻,定义预测状态的初始值为当前时刻的实际状态x(k|k)=x(k),利用机载探测设备探测环境中的障碍物i状态,并判断无人机与障碍物i间的距离是否满足避障功能触发条件Doi(k)≤Ra+Roi,根据式(25)选择Joi(k)的形式; 步骤2:求解优化问题(27)得到最优控制序列u*(k+l|k), 0≤l≤N-1; 步骤3:将最优控制序列的首项作为实际控制输入应用于无人机中,即u(k)=u*(k|k); 步骤4:在k+1时刻,基于新的状态测量值x(k+1),循环运行步骤1—步骤4。 根据第1、2节的描述,给出四旋翼轨迹规划与跟踪控制的整体框图,如图4所示。其中自动驾驶仪采用常见的PID控制方法实现速度控制。pRadau表示利用伪谱法直接求得的最优轨迹,pr表示经过均匀采样、线性插值后得到的参考轨迹。 图4 四旋翼轨迹规划与跟踪控制整体框图Fig.4 Overall block diagram of the trajectory planning and tracking control of quadrotor 3.1.1轨迹规划阶段的参数 表1为四旋翼无人机参数表;表2为雷达参数表,包括2个雷达;表3为路径约束。 表1 四旋翼无人机参数 表2 雷达参数 表3 路径约束 四旋翼无人机的边界条件: X(t0)=(0,0,-100,0,0,0,0,0,0,0,0,0)T X(tf)=(0,900,-100,0,0,0,0,0,0,0,0,0)T 即无人机初始位置为(0,0,-100)T,目标位置为(0,900,-100)T,因为选用北东地坐标系,所以z轴的值为负值时表示在地面以上。目标函数中的权重系数分别为w1=1,w2=1。 3.1.2轨迹跟踪控制阶段的参数 设置四旋翼的控制增益lv=3,安全半径Rs=0.8 m,避障触发半径Ra=20 m,目标函数中的权重矩阵Q=diag(1,1,1),S=diag(1,1,1)。采样时间为0.5 s,假设无人机自身实际位置更新频率为2 Hz。 表4为无人机状态、输入约束,注意轨迹跟踪控制阶段的速度上限设置值应比轨迹规划阶段的设置值略大,否则无人机可能无法跟踪上参考轨迹。 表4 状态、输入约束 设置了2个匀速运动的动态障碍,其中动态障碍1的半径为Ro1=1.5 m,初始位置为(-17,2,-108)Tm,速度为(0,8,0)Tm/s;动态障碍2的半径为Ro2=2 m,初始位置为(0,102,-112)Tm,速度为(-4,0,0)Tm/s。避障惩罚代价中的参数λ=500,σ=2。 图5是利用hp自适应Radau伪谱法直接求得的3个方向的位置变化曲线,无人机到达指定目标点所需飞行时间约为91.47 s。从图5中可以看出,位置曲线是较为平滑的,但是从第20~26 s的局部放大图中可见,所规划的轨迹点是不均匀的,因此需要进行均匀化处理。图6为经过均匀采样、线性插值后得到的位置变化曲线,采样时间为0.5 s。从第20~26 s的局部放大图中可见,此时轨迹点已均匀。 图5 利用伪谱法得到的位置变化曲线Fig.5 Curves of position obtained by pseudospectral method 图6 均匀采样、线性插值后的位置变化曲线Fig.6 Curves of position after uniform sampling and linear interpolation 图7中五角星表示目标点位置,2个半球表示2个雷达的探测范围。虚线表示参考轨迹,即图6的三维轨迹形式,实线为无人机的实际跟踪轨迹,轨迹上的圆圈为每隔5 s无人机所在的位置。由图7中可见,所规划的轨迹能够避开雷达威胁,且能够到达目标点。 图7 参考轨迹与实际轨迹Fig.7 Reference trajectory and actual trajectory 图8为图7的局部放大图,展示了无人机避障的细节,其中将第6 s、第11 s的无人机位置用黑色球来表示,对应时刻的障碍物位置用灰色球来表示,虚线为无人机参考轨迹,实线为无人机实际轨迹,灰色点线为障碍物运动路线。由图8可见,无人机能够主动偏离参考轨迹来避开动态障碍物。 图8 三维轨迹局部放大图Fig.8 Local enlargement of the 3D trajectory 图9为3个方向的位置跟踪误差曲线,e=pr-p=(ex,ey,ez)T。 图9 位置跟踪误差Fig.9 Position tracking error 图10为无人机与障碍物间的距离变化曲线,图11为参考速度、期望速度、实际速度。由于无人机是由悬停状态开始执行任务,在0~3 s内,虽然无人机在加速,但是其实际速度一直小于参考速度(见图11),因此y方向的位置误差一直在增大。在3.5~13.5 s内,无人机为避免与障碍物碰撞而暂时偏离参考轨迹(见图10),因此这段时间的跟踪误差相对较大。在91~97 s内,由于在无人机到达目标点后,存在超调影响(见图11),因此跟踪误差表现为先增大后减小。在其他时间段,各方向的跟踪误差均小于1 m。 图10为0~18 s内无人机与障碍物之间的距离变化曲线,其中带点的实线为无人机与障碍物1之间的距离变化曲线,图片下方的虚线为安全临界值(Rs+Ro1)=2.3 m,Do1>2.3 m表明无人机未与障碍物1发生碰撞,图片上方的虚线为避障触发临界值(Ra+Ro1)=21.5 m,当Do1≤21.5 m时,将触发避障功能;带叉的实线为无人机与障碍物2之间的距离变化曲线,图片下方的点线为安全临界值(Rs+Ro2)=2.8 m,上方的点线为避障触发临界值(Ra+Ro2)=22 m。易知,无人机也未与障碍物2发生碰撞。 图10 无人机与障碍物间的距离Fig.10 Curves of the distance between UAV and obstacles 图11 参考速度、期望速度、实际速度Fig.11 Reference velocity,desired velocity and actual velocity 图11中虚线为轨迹规划生成的参考速度,点线为利用模型预测控制生成的期望速度,实线为无人机实际速度。可见,各个速度均满足所设置的约束。在t=3.5 s时,由于此时无人机与障碍物1的距离小于避障触发临界值(见图10),因此触发避障功能,由MPC生成的期望速度开始明显偏离参考速度,而在t=13.5 s后无人机与障碍物的距离大于避障触发临界值,因此由MPC生成的期望速度又逐渐接近参考速度。与图8中位置跟踪误差的变化现象相符。 图12 无人机与障碍物间的距离(对比实验)Fig.12 Curves of the distance between UAV and obstacles (comparison experiment) 为进一步说明本文中算法的优越性,基于文献[20]中的人工势场(artificial potential field,APF)算法设计对比实验。图13为APF算法下的位置跟踪误差曲线,对比图9可见,在40~60 s内,APF算法的跟踪误差明显较大,x和y方向的位置误差值约为5 m,而本文中算法的误差值几乎为0。 图13 位置跟踪误差(APF算法)Fig.13 Position tracking error(APF method) 图14为APF算法下x方向的参考速度、期望速度、实际速度曲线。由于APF算法无法有效考虑无人机的输入约束,因此其生成的期望速度值有大于13 m/s的现象,然而基于MPC的算法可以显示考虑输入约束,保证其生成的期望速度满足输入约束。 图14 x方向的参考速度、期望速度、实际速度 (APF算法)Fig.14 Reference velocity,desired velocity and actual velocityin x-axis(APF method) 1) 经过统筹、协调设计的四旋翼轨迹规划与跟踪控制算法能够较好地完成想定的低空突防任务,即能够控制四旋翼无人机快速穿越雷达与移动障碍并存的威胁环境并到达指定目标点。 2) 在跟踪控制算法的避障惩罚函数中考虑障碍物的预测位置值,能够更好地应对移动速度较快的障碍物。
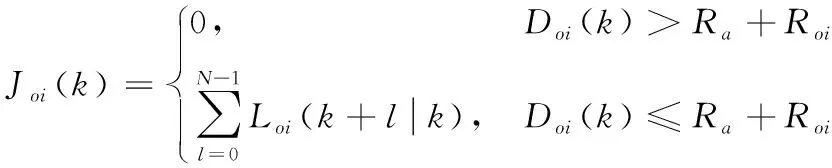
2.2 基于MPC的跟踪控制算法


3 仿真结果及分析
3.1 参数设置

3.2 结果及分析







4 结论

