电磁释放锁在起落架落震试验中的应用与动力学过程研究

黄兆铭

（中国飞机强度研究所强度与结构完整性全国重点实验室，陕西 西安 710065）

飞机起落架是飞机结构的重要部件之一，用于承受机身重量并在滑跑、起飞、着陆吸收相应的载荷，关乎飞机起飞与着陆过程的安全性。为研究起落架的结构强度和缓冲性能，需要开展起落架落震试验以模拟飞机着陆过程。根据试验目的，落震试验可分为选参试验与验证试验，国内军用标准67.9A 对此有明确规定，其中验证性试验是在起落架缓冲系统在满足吸收能量的条件下，验证其撞击载荷、结构和充填参数与设计要求的符合性，而选参实验是在飞机研制阶段，调节起落架参数开展落震试验以改进缓冲性能。试验要求对飞机的着陆速度等参数进行模拟，并测量起落架的载荷与变形等响应，国军标67.4A 对陆基飞机的着陆速度要求如表1 所示。

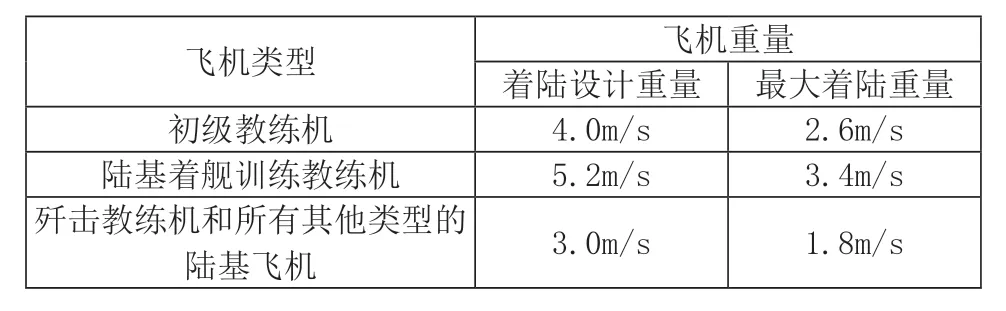
表1 陆基飞机的着陆速度要求

由起落架典型的二质量模型以及基于能量法的落震试验评定准则可知，起落架下沉速度作为试验的输入参数，是起转回弹载荷、缓冲器行程等参数的决定性要素之一，将对测试得到的载荷和变形响应等数据有较大影响，从而影响用于考核起落架缓冲性能的测试功量，因此，试验过程需要精准把握起落架下沉速度，确保试验的有效性和准确性。以往的落震试验采用机械锁进行落体的提升与释放，但机械锁多次使用后存在机构变形、安全性降低的情况，电磁锁相比机械锁具有安全可靠、施放时间短等特点，在试验的提升阶段电磁锁通过磁力吸附重物，在释放阶段，通过消去电磁锁的磁力使重物自由落体。但由于电磁锁自身设计的原因，往往在释放过程中，电磁锁难以达到瞬间快速消去磁力，使重物在下落过程中，未能达到理想的自由落体，下沉速度呈非线性增长，在一定的投放高度下，会出现着陆速度低于目标值的情况，使试验失去有效性。基于起落架落震试验与释放过程电磁锁的磁力变化建立数学模型，并通过数值计算分析试验系统不同参数对起落架着陆速度的影响，最后，基于该模型提出一种可应用于起落架落震试验的投放高度修正方法，为试验中下沉速度的精确模拟提供有效的理论方法。

1 起落架落震试验

落震试验是在立柱式试验台上将起落架与配重形成一个整体的落体系统，提升至一定高度后释放，模拟飞机起落架在着陆过程中的动力学过程。落震试验系统包括多个子系统，由试验台架、提升/释放装置、航向速度模拟装置、升力模拟装置以及数据采集系统等子系统组成。

当飞机两点着陆时，单个主起落架上承受的当量质量为：

式中，M 为飞机着陆质量。当飞机三点水平着陆时，可根据力的平衡方程分别计算前起落架与主起落架承受的当量质量：

式中，Mqd为前起落架上的当量质量，Mzd为主起落架上的当量质量，a 为停机状态下飞机重心到前起落架轮轴的水平距离，b 为停机状态下飞机重心到主起落架轮轴的水平距离，h 为缓冲器全伸长时飞机重心与主起落架轮轴的高度差，为平均滑动摩擦系数。基于能量等效原则的落震试验，起落架缓冲系统的动力过程可分为压缩和反弹两个阶段。对于压缩行程，在一定着陆速度的初始条件下，投放高度为：

缓冲系统需要吸收的总能量为：

式中，A 为缓冲系统在压缩阶段吸收的总能量，md为当量质量，Vy为着陆速度。缓冲系统包含轮胎与缓冲器，两者吸收的能量分别为：

式中，At为轮胎吸收的能量，Kt为轮胎刚度，yt为轮胎垂向压缩量，Aabs为缓冲器吸收的能量，Fs为缓冲器的随行程变化的轴向力，s 为缓冲器压缩行程。

根据上述公式，可得到缓冲器吸收的能量占总能量的比值为：

对于使用减缩质量法的落震试验，需要遵循机轮不能跳离台面的要求，因此，缓冲系统消耗的能量要不小于跳离所需的临界能量：

其中，Ccr为起落架跳离地面的临界能量值，X 为缓冲器的热耗系数，可通过下式计算：

式中，ygc为起落架上部质量的总位移量，g 为重力加速度。对于使用仿升法的落震试验，起落架允许一定程度的弹跳，其反弹高度可表示为：

由此可知，在起落架压缩阶段缓冲器吸能占比与系统的着陆速度相关，并且在起落架反弹阶段，两种试验方法的反弹高度都受到着陆速度的影响，在调参落震试验过程中，往往需要根据缓冲系统的吸能效率以及反弹离地情况，开展参数调节以优化起落架性能，所以起落架的着陆速度将是关乎试验的准确性以及起落架缓冲性能分析的重要因素。

2 电磁锁释放落体的数学模型

起落架落震试验系统包括电磁锁子系统，该子系统用于试验件及试验夹具的锁持提升与释放，其包含提升作动筒、释放锁、导向锁架和控制系统等部分。电磁锁的基本原理是操作人员发送充磁或消磁的指令后，控制系统释放短时间的电磁脉冲作用在磁吸面上，改变其磁场特性，达到充磁或消磁的效果。在试验落体的释放过程中，由于脉冲作用并非瞬时完成，电磁锁磁力不能实现瞬间消去，存在一定的衰退时间，因此重物受到的磁吸力特性为随时间和间隙距离（电磁锁与磁吸面板之间）的变化而衰减。设磁力随时间的衰减系数为gt，随间隙距离的衰减系数为，分别表示为gs：

式中，t 为释放后的时间，tcr为磁力随时间衰减为零的临界时间，y 为上部质量行程，ycr为磁力随间隙大小衰减为零的临界行程。假设磁力受时间影响与受间隙距离影响不相关。起落架开始释放阶段，电磁锁作用在重物上的磁力表示为：

式中，fo为电磁锁最大磁力，y 为上部质量行程。电磁锁释放后落体的动力学方程为：

式中，G 为落体重量，即起落架、配重和夹具的重量之和，f 为落体与试验台架之间的摩擦力。对上述方程进行降阶，可得：

式中，Vy即起落架着陆速度。

3 落震着陆速度影响因素及分析

基于第3 节建立的电磁锁释放落体数学模型，针对不同电磁锁参数以及投放质量对起落架着陆速度的影响展开讨论，令落体系统与试验台架之间的摩擦力f=0。本文以目前落震试验主要使用的电磁锁型号作为计算对象，最大有效磁力为25t。由于低投放高度的工况受到影响更显著，因此选取试验工况为表格1 中的“歼击教练机和所有其他类型的陆基飞机”在最大着陆重量工况进行投放，即目标着陆速度为，由式（3）可知，理论投放高度为0.165m。

3.1 磁力随间隙距离衰减

针对磁力随间隙距离衰减对起落架落震着陆速度的影响开展分析，磁力随间隙距离变化的典型特性曲线如图1 所示，针对采用不同特性曲线的电磁锁，计算起落架的着陆速度与误差大小，起落架下落至接触测力平台时终止计算。设3 种型号电磁锁的磁力随时间呈线性衰减，临界时间均为0.5s，落震试验投放质量为15t。

图1 磁力随间隙距离衰减曲线

计算得到的起落架行程曲线如图2 所示，因为假定三种型号的电磁锁临界时间一致，因此起落架开始下行的时间点均约为0.2s。开始下落后，因为受磁力变化特性的影响，采用电磁锁3#的起落架最先着地，采用电磁锁1#的起落架最后着地，采用三种电磁锁的起落架触台时间分别为457ms、450ms、441ms，触台时间较为接近，表明磁力随间隙距离衰减特性对起落架触台时间影响较小。起落架触台速度误差如表2 所示，起落架下落加速度时程曲线如图3 所示。由起落架下落加速度曲线可知，加速度增长至9.8m/s2最晚时间为350ms，早于磁力随时间衰减的临界时间值，这表明此时磁吸面板与重物之间的间隙距离对磁力的影响占主导作用。对比三种特性曲线，随间隙距离衰减最快的电磁锁3#，对应的起落架加速度曲线斜率最大，下沉加速度最先达到9.8m/s2，从而使最终着陆速度误差比较小，为1.00%；随间隙距离衰减最慢的电磁锁1#，起落架加速度曲线开始时与3#曲线较为接近，随后差异逐渐增大，最终着陆速度误差较大，达到1.89%。电磁锁采用不同衰减特性曲线，对起落架着陆速度的误差变化影响较为显著。

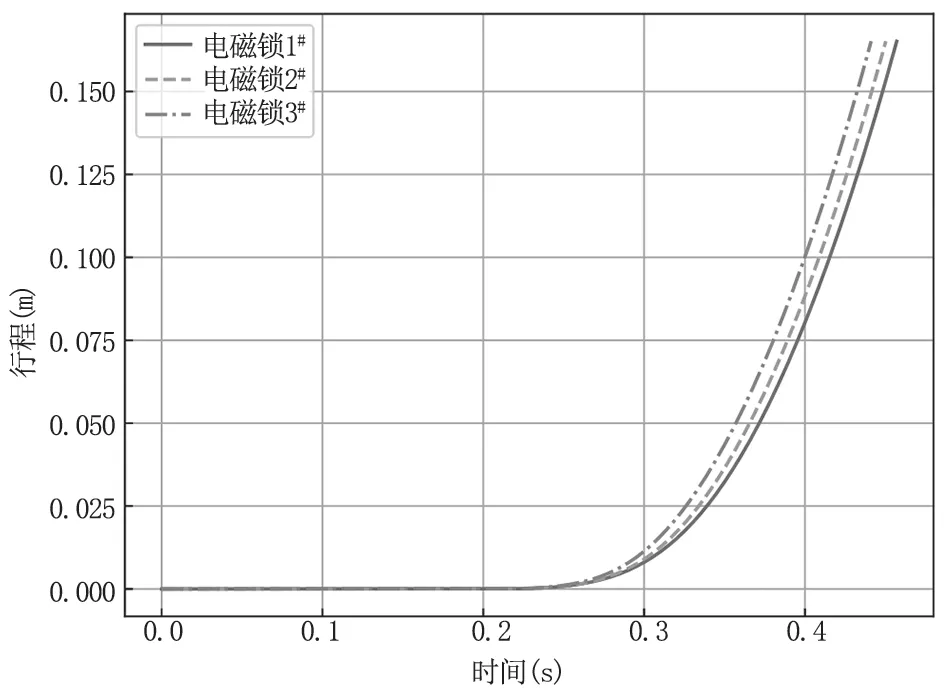
图2 起落架行程曲线（1）

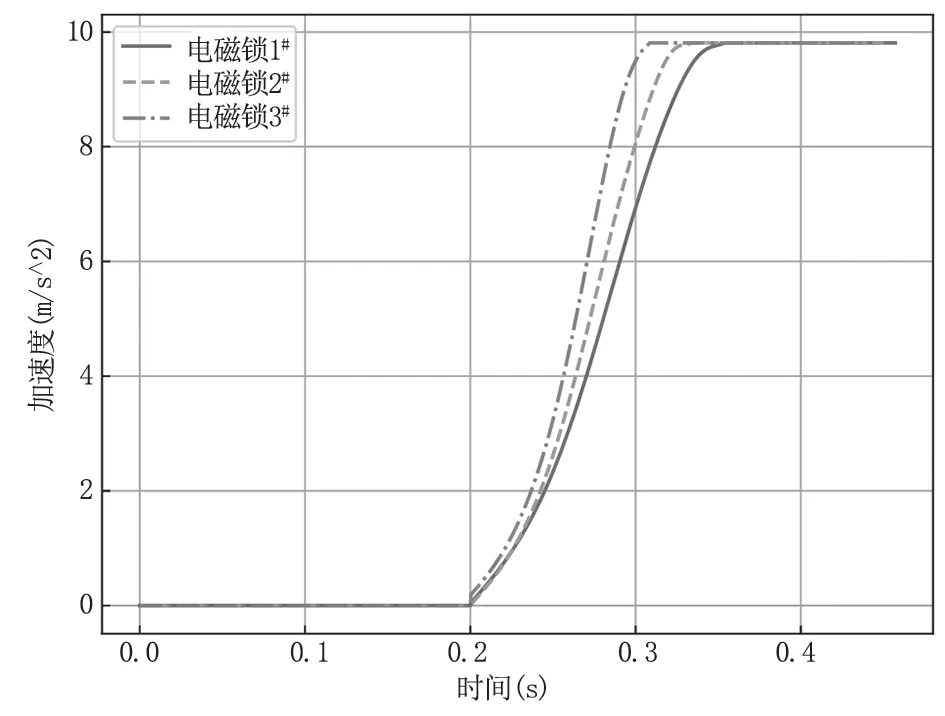
图3 起落架下落加速度时程曲线（1）

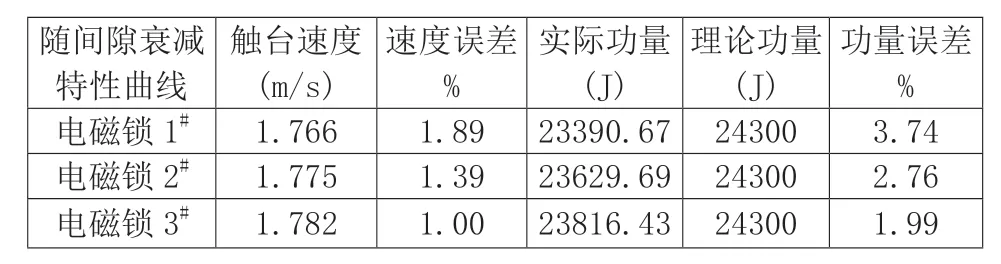
表2 触台速度与功量误差（1）

根据标准规范所要求的功量误差，单次落震试验的功量误差必须不超过3%。由表格2 可知，在不考虑立柱与导论之间的摩擦、吊篮与立柱之间的间隙等因素影响的前提下，由于触台速度所造成的功量误差最大已达到3.74%，该次试验投放无效，这表明电磁锁性能对起落架触台速度的影响将直接关系到试验的有效性。

3.2 磁力随时间衰减速率

针对磁力衰减速率对起落架落震着陆速度的影响开展分析，假设电磁锁磁力随时间呈线性衰减。本节计算的电磁锁，磁力随间隙距离衰减的特性曲线以图1 中的电磁锁2#为例，投放质量为15t。分别计算临界时间为0.2s、0.4s、0.6s、0.8s、1.0s 这5 种情况下起落架的着陆速度，各工况计算至起落架触台时终止。得到的起落架行程时程曲线如图4 所示，由图可知，临界时间每相差0.2s，造成起落架下落的开始时间相差约0.1s，起落架触台时间也相差约0.1s，磁力衰减的临界时间大小对起落架下落行程的时间长短有较明显的影响。

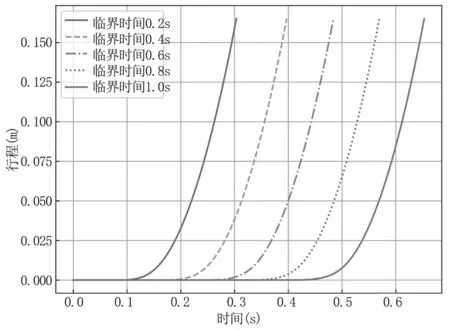
图4 起落架行程时程曲线（2）

起落架下落加速度时程曲线见图5，由加速度时程曲线可知，所有工况条件下起落架着陆加速度最终均能达到理想的重力加速度9.8m/s2，但因为释放时存在磁力的持续作用，起落架下落的加速度未能在释放时立刻达到9.8m/s2。在不同电磁锁临界时间的条件下，起落架加速度曲线的斜率不一致，临界时间越大，下沉加速度曲线斜率减小越显著，使得加速度增长更为缓慢，起落架从开始下落到加速度达到9.8m/s2所需时间分别为107ms、128ms、138ms、145ms、150ms。起落架下落加速度曲线图中，临界时间为0.4s、0.6s、0.8s、1.0s的加速度曲线在接近9.8m/s2的拐点处出现突变，这是因为当间隙距离达到电磁锁2#的临界值25mm 时，磁力随间隙距离已变为0，此时重物已不受向上的磁力作用，加速度突变为9.8m/s2，在这种情况下，间隙距离对磁力的影响占主导作用，且临界时间越大突变越明显，临界值为0.1s 的电磁锁则是临界时间对磁力的影响占主导作用，这表明磁力的衰减速率随间隙和随时间变化，两者中的较大者起到了主要影响作用。计算得到的触台速度误差见表3，触台速度的误差随临界时间增大而增大，采用临界时间为0.2s 的电磁锁着陆速度误差最小，为0.89%；采用临界时间为1.0s 的电磁锁着陆速度误差最大，达到1.67%。当电磁锁临界时间大于0.4s，功量误差已达到规范标准要求的3%，此时，电磁锁对起落架触台速度的影响不可忽视。

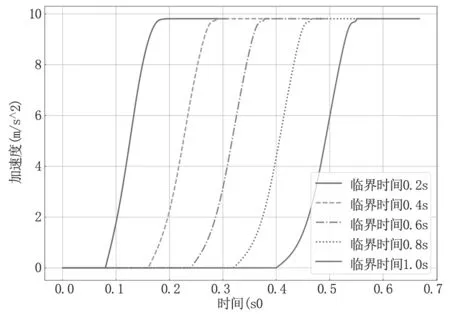
图5 起落架下落加速度时程曲线（2）

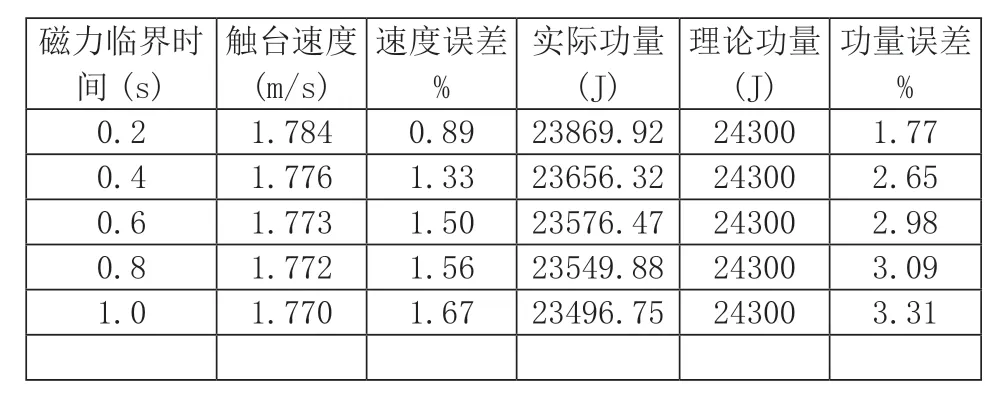
表3 触台速度与功量误差（2）

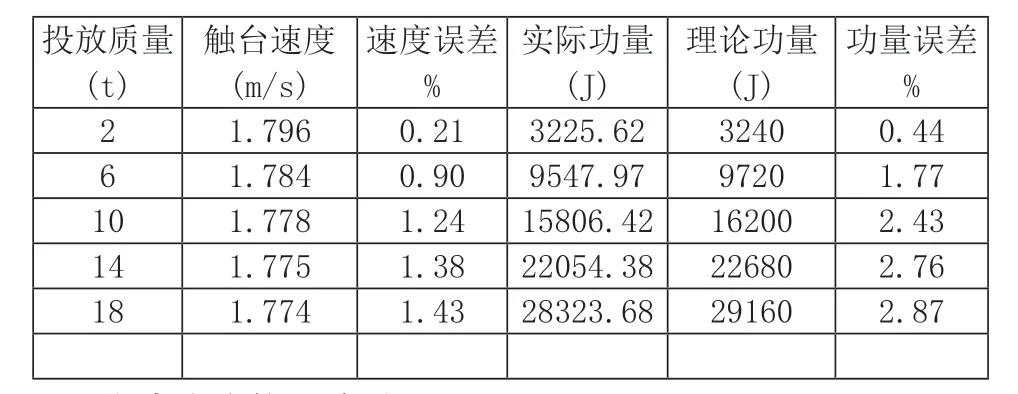
表4 触台速度与功量误差（3）

3.3 投放质量

对于指定量级的落震试验台，在额定提升能力的条件下，往往需要满足不同投放质量的要求，针对投放质量对起落架着陆速度的影响开展分析。设电磁锁临界时间为0.5s，随间隙距离衰减曲线采用图1 所示的电磁锁2#，额定提升能力为25t，分别投放质量为2t、6t、10t、14t、18t 的落体系统。起落架下落的行程曲线如图6 所示，由图可知，在电磁锁参数特性一定的条件下，投放质量越大，则落体系统开始下行的时间点越早，触台时间分别为662ms、607ms、540ms、468ms、395ms。

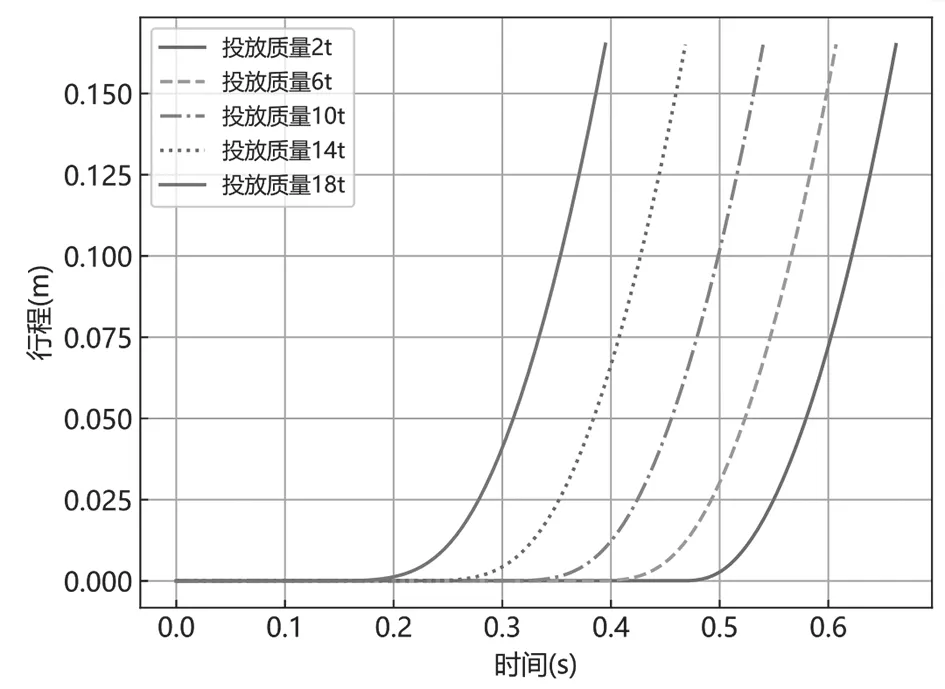
图6 起落架行程时程曲线（3）

起落架下落加速度曲线如图7 所示。由图可知，投放质量为2t 的曲线斜率接近直线，加速度能够在开始下落行程后40ms 以内迅速达到目标值9.8m/s2，起落架着陆速度误差仅0.21%，实际功量误差0.44%，试验投放效果较为理想。当投放质量增大，加速度曲线的斜率有明显的降低，起落架加速度从0 到9.8m/s2所需时间最大为137ms，最终着陆速度误差与投放质量呈正相关关系，当投放质量大于等于10t 时，功量误差接近3%。这表明在确定的电磁锁特性参数条件时，投放质量越大，电磁锁磁力衰减延迟对起落架着陆速度和功量误差影响越显著。

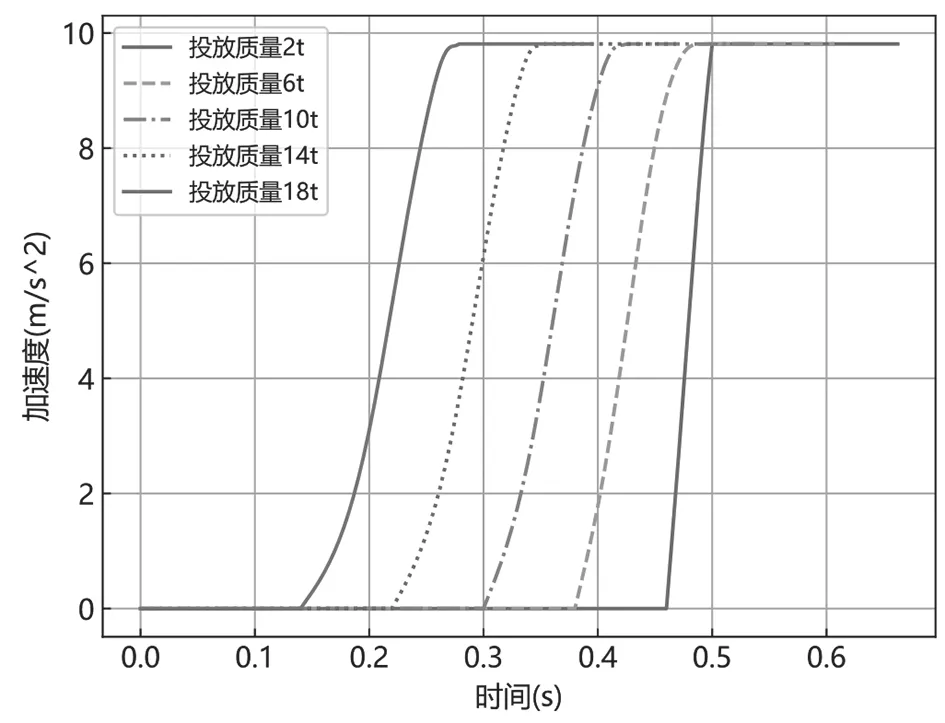
图7 起落架下落加速度时程曲线（3）

4 着陆速度修正方法

由上述分析可知，电磁锁的参数特性以及投放重物的质量将对起落架着陆速度造成误差，影响试验的有效性和准确性。由于试验中无法直接测量着陆速度，仅能通过对落体的位移进行差分计算得到，难以准确修正着陆速度。因此，对于着陆速度导致的功量误差，为了满足落震试验标准所要求的误差范围，试验人员往往需要花费大量时间对投放质量进行反复迭代，以修正功量减小误差。本文基于第三节的释放落体数学模型，提出一种针对电磁锁参数特性的着陆速度修正方法：（1）首先基于数学模型（式11 ～式16）以及电磁锁参数特性（磁力随间隙距离衰减曲线以及临界时间值）建立方程组；（2）给定投放质量和理想状态下的投放高度H0等前提条件，通过欧拉法或龙格库塔等方法求解方程组，得到起落架着陆速度V0和下落加速度时程曲线，根据计算结果判断着陆速度和投放功量是否满足要求；（3）因为起落架下落速度随投放高度单调递增，基于二分法迭代计算上述方程组。通过给定投放高度增量ΔH0，得到新的投放高度，利用数值方法求解方程组得到着陆速度V1；（4）若着陆速度大于理想值，则修正高度增量为-ΔH/2，若着陆速度小于理想值，则修正高度增量为ΔH/2，得到新的投放高度作为求解方程组，更新高度增量；（5）重复此步骤，直到着陆速度满足要求。

5 结语

本文首先介绍了起落架落震试验方法及试验系统构成，根据试验释放落体所用的电磁锁建立了分析模型，该模型考虑了磁力随间隙距离衰减以及随时间衰减的特性，并基于该模型分析了不同特性参数和投放质量对着陆速度和功量的影响，得到以下结论。

（1）电磁锁磁力衰减特性对起落架着陆速度的影响不可忽视，由于着陆速度误差造成的功量误差大于3%，超出了标准规范要求范围；（2）着陆速度误差均与电磁锁磁力衰减的临界时间和临界间隙距离呈正相关关系；（3）电磁锁磁力的衰减速率随间隙和随时间变化，两者中的较大者起到了主要影响作用，可针对其中的主要影响因素采取必要的改型措施；（4）在电磁锁参数特性一定的条件下，投放质量越大，起落架着陆速度误差越大。本文最后根据电磁锁释放落体的模型，构建了可应用于实际试验的起落架着陆速度修正方法。