随机风振作用下非对称悬挂结构响应及等效风振力研究

梁雄杰　杨宗旺　陈敏　张梨荣　葛新广

摘 要：针对非对称悬挂结构在随机风振作用下动力响应分析复杂的问题，提出其在顺风向作用下水平和竖向耦合振动响应的分析方法。首先，建立非对称悬挂结构在顺风向脉动风振作用下水平和竖向耦合振动的动力方程，利用实模态振型分解法获得以实模态广义坐标表示的风振动方程，并利用有限元软件获得实模态振动参数；然后，基于复模态法和虚拟激励法获得悬挂结构位移、速度、实模态广义坐标等响应量的统一形式频域解，并基于二次式分解法获得了上述响应量谱矩和方差的简明封闭解以及非对称悬挂结构在顺风向风荷载作用下结构等效风振力的计算式；最后，通过算例分析，验证了所提封闭解的正确性，并研究了非对称悬挂结构动力响应及等效风振力受广义坐标的影响。研究表明，在顺风向风荷载作用下，结构将同时产生横向与竖向振动，且竖向振动不可忽略。

关键词：非对称悬挂结构；随机风振；封闭解；等效风振力

中圖分类号：TU312.1；TU352.2 DOI：10.16375/j.cnki.cn45-1395/t.2023.04.005

0 引言

悬挂结构作为一种新型建筑结构体系，具有强烈艺术表现力，应用于大型图书馆[1]、大剧院[2]、体育馆[3]等公共建筑中。悬挂结构通过水平承重结构和吊杆将楼层悬吊在竖向结构上，结构竖向荷载通过吊杆传送到主要承重构件上，可在遭受外部动力荷载时发挥良好的抗风、减震性能。风荷载不仅具有随机振动的特点，而且是建筑结构设计中极为重要的作用力之一。蔡文华等[4]研究了核筒悬挂结构顺风向脉动风压作用下的结构动力学特性，研究表明核筒悬挂结构具有良好的抗风、减振特点。当风荷载仅采用由Davenport风速谱生成的时程荷载时，所得结论基于确定性时程曲线具有一定的局限性。Davenport风速谱作为一种随机激励，采用随机理论进行风振响应分析对广大风振效应更具有普遍性。

基于随机激励下的结构风振响应分析，主要有Monte Carlo方法[5-6]、时域法和频域法3类[7-9]。Monte Carlo方法将随机风振激励的功率谱密度函数按照特定方法生成大量的时程曲线，并利用动力学理论获得结构响应量的时程曲线，最后利用统计学理论获得结构响应量的方差，是目前分析脉动风荷载作用结构响应分析的重要方法之一[10-11]。从本质上说该方法是最准确的一种方法，但计算量异常大，不利于实际工程应用。时域法中结构响应的协方差表示为风激励协方差与结构脉冲函数的二重积分，而现行规范脉动风荷载主要采用Davenport谱和Kamal谱，两者均为无理式功率谱，没有协方差表达式，故时域法都是对风速谱做近似处理后应用[12-13]。频域法中，结构响应的功率谱表示为风激励功率谱与结构响应量频响函数模值平方的乘积，因具有简洁明了的代数关系，有着广泛工程应用，虚拟激励法是其典型代表，然而频域法应用时需要对响应功率谱进行数值积分，存在计算效率和精度受积分方法影响的问题[9，14-15]。葛新广等[7-8，15-16]结合时域法和频域法的各自优点提出了基于随机激励下结构响应封闭解法，并将其应用于建筑结构和桥梁结构的地震动响应和风振响应分析。

为更好地实现建筑布置，悬挂结构仅在一侧设置悬挂体系，形成了非对称悬挂结构，在水平方向动力荷载（如风）和地震会使悬挑结构同时产生水平运动和竖向运动，属于典型的水平和竖向耦合运动，而目前国内外相关研究极为匮乏。因此，利用随机振动理论研究顺风向水平风荷载作用下非对称悬挂结构的随机响应具有重要的工程应用价值。

1 非对称悬挂结构在随机风振激励下响应封闭解

建筑结构的动力分析，集中质量法是目前最常用的方法。基于Midas Gen软件，对结构进行建模，39个节点考虑水平和竖向运动，共78个自由度。节点集中质量由结构自重、楼面铺装自重和活荷载组成，三者形成的集中质量按从属面积法计算；本算例中楼面铺装取1.0 kN/m2，活荷载取1.5 kN/m2（规范值的一半）。结构体系刚度计算按结构力学方法进行，考虑楼板对梁刚度的贡献，规范里一般按梁刚度的2倍计算。对于钢结构构件对应的节点位移，根据规范，阻尼比取2%，对于钢筋混凝土结构对应的节点位移进行分析时阻尼比取5%，对于两种材料连接点进行分析时，阻尼比按较小阻尼取值。建筑所在场地风荷载地面粗糙度为A类，基本风压w0=0.4 kN/m2。脉动风采用Davenport风速谱，Kr=0.001 29；[V10]=24.85 m/s；[μs（Hi）=1.4]；[μz（Hi）]按照现行规范取值。

3.1 封闭解的验证

虚拟激励法[10]广泛应用于各类工程动力响应分析，是目前分析随机激励下的结构动力响应常用的方法之一。然而该方法在计算结构响应0-2阶谱矩和方差时，需要数值积分，存在计算精度和效率的问题。为了验证本文方法的正确性，利用虚拟激励法进行验证。下面给出虚拟激励法求解悬挂结构响应谱矩的计算式。

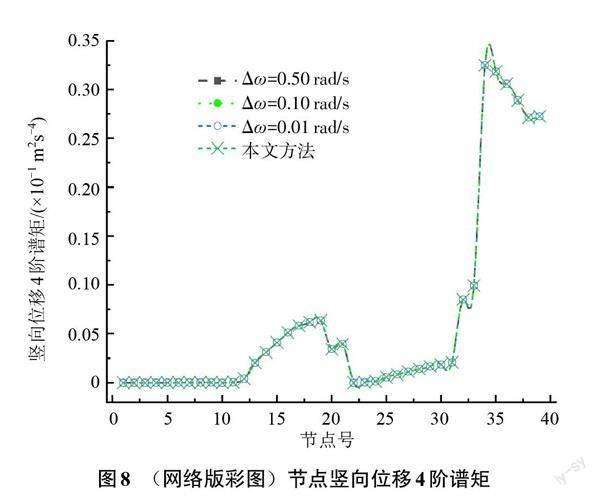
考虑前20阶振型，按虚拟激励法和本文方法分别计算结构顺风向位移和竖向位移的0阶、2阶和4阶谱矩对比图，如图3—图8所示。

从图3—图8可知，随着虚拟激励法中积分步长的缩短，其计算结果趋于稳定，且稳定结果与本文方法趋向一致。上述结果证实本方法的正确性。从计算效率上分析，虚拟激励法工况1耗时14.87 s，工况2耗时91.73 s，工况3耗时725.50 s，而本文方法耗时仅为0.14 s。上述结果证实本文方法相比虚拟激励法具有高效性。

3.2 等效风荷载力计算

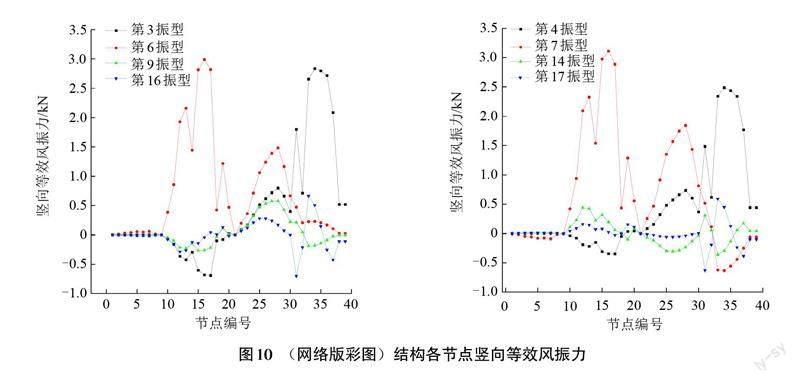
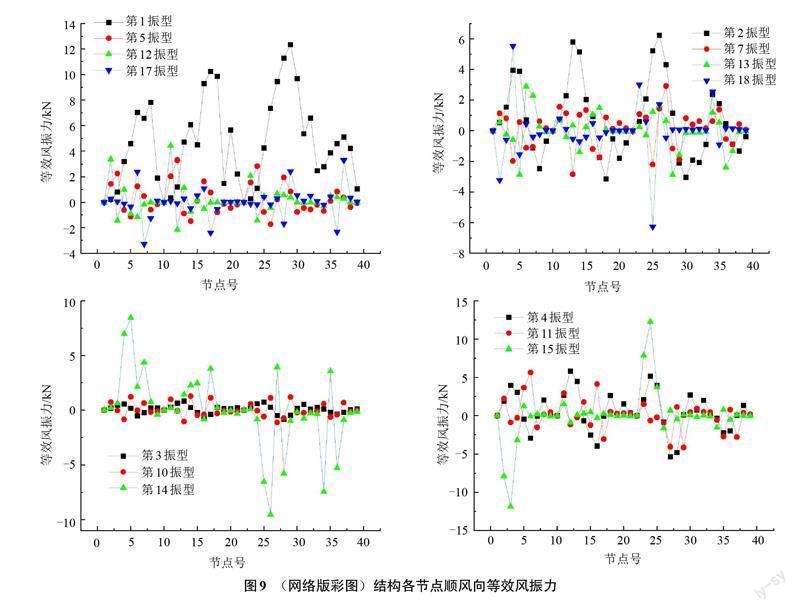
利用式（25）可获得悬挂结构具有影响的振型的节点处的等效风荷载，如图9和图10所示。由图9可知，在20个振型中，有14个振型所对应的顺风向等效风振力较大，其中第1、2、4、14、15及18振型所对应的等效风振力较大。故针对悬挂结构需要考虑多个振型所产生的响应。由图10可知，在20个振型中，有8个振型所对应的竖向等效风振力较大，其中第3、4、6及7振型所对应的等效风振力较大。故针对悬挂结构需要考虑多个振型所产生的响应。与顺风向风振力相比，竖向风振影响显著，必须考虑竖向振动的影响。

4 结论

论文针对非对称大跨悬挂结构在顺风向风荷载作用下结构产生竖向和水平向耦合振动的响应分析，提出了悬挂结构体系的位移、广义坐标、等效风力等随机响应的封闭解法，主要结论如下：

1）通过结合采用Midas Gen软件获得了非对称悬挂结构的振型、自振圆频率和节点集中质量等结构振动参数，基于随机振动理论和Davenport风速谱建立非对称悬挂结构随机风振动力方程。

2）基于实模态解耦法，将悬挂结构的动力位移表示为振型和由广义坐标所表示的振动方程的线性组合，并采用复模态法和虚拟激励法获得了广义坐标及节点位移的统一形式的频域解，从而得到了悬挂结构广义坐标、节点位移及节点等效风振力方差的简明封闭解。基于所得封闭解分析了非对称悬挂结构在横向振动和竖向振动响应随振型和广义坐标的影响规律。结果表明：在顺风向风荷载作用下，结构将同时产生横向与竖向振动，且竖向振动不可忽略。

参考文献

[1] 肖魁，贾水钟，贾君玉，等. 上海图书馆东馆悬挂结构方案设计与研究[J]. 建筑结构，2022，52（1）：1-6.

[2] 张瑾，杨德健. 大跨度复杂空间悬挂结构自振特征与动力性能分析[J]. 河北水利电力学院学报，2021，31（1）：22-26，31.

[3] 朱前坤，蒲兴龙，惠晓丽，等. 基于人群-结构耦合作用甘肃省体育馆悬挂结构振动舒适度评估及控制[J]. 工程力学，2018，35（S1）：46-52.

[4] 蔡文华，张继文，涂永明，等. 核筒悬挂建筑结构体系的顺风向风致响应分析[J]. 工程力学，2011，28（6）：103-109.

[5] BAYRAK G，ACAR E. Reliability estimation using Markov chain Monte Carlo-based tail modeling[J]. AIAA Journal，2018，56（3）：1211-1224.

[6] KUMAR A，SAHA S K，MATSAGAR V A. Stochastic response analysis of elastic and inelastic systems with uncertain parameters under random impulse loading[J]. Journal of Sound and Vibration，2019，461：114899.

[7] 葛新广，龚景海，李创第，等. 功率谱二次正交化法在随机地震动响应的应用[J]. 振动工程学报，2022，35（3）：616-624.

[8] GE X G，GONG J H，ZHAO C J，et al. Structural dynamic responses of building structures with non-viscous dampers under Kanai-Tajimi spectrum excitation[J]. Journal of Sound and Vibration，2021，517：116556.

[9] 林家浩，张亚辉，赵岩. 虚拟激励法在国内外工程界的应用回顾与展望[J]. 应用数学和力学，2017，38（1）：1-32.

[10] YIN X F，SONG G B，LIU Y. Vibration suppression of wind/traffic/bridge coupled system using multiple pounding tuned mass dampers（MPTMD）[J]. Sensors（Switzerland），2019，19（5）.DOI：10.3390/s19051133.

[11] YANG W C，DENG E，LEI M F，et al. Transient aerodynamic performance of high-speed trains when passing through two windproof facilities under crosswinds：a comparative study[J]. Engineering Structures，2019，188：729-744.

[12] 李暾，张梦丹，姜琰，等. 基于近似Davenport风速谱的建筑结构动力响应的新封闭解法[J]. 广西科技大学学报，2020，31（4）：1-10，18.

[13] 李创第，王磊石，邹万杰，等. 广义Maxwell阻尼器高层结构随机风振响应解析法[J]. 广西大学学报（自然科学版），2016，41（4）：953-963.

[14] 赵中伟，张永高. 基于本征-虚拟激励法的大跨钢结构风振响应分析[J]. 空间结构，2020，26（1）：15-23.

[15] GE X G，LI C D，AZIM I，et al. Structural dynamic responses of linear structures subjected to Kanai-Tajimi excitation[J]. Structures，2021，34：3958-3967.

[16] 葛新广，张梦丹，龚景海，等. 频响函数二次正交法在Davenport风速谱下结构系列响应简明封闭解的应用研究[J]. 振动与冲击，2021，40（21）：207-214.

[17] 李创第，葛新广，朱倍权. 带五种被动减振器的高层建筑基于Davenport谱随机风振响應的解析解法[J]. 工程力学，2009，26（4）：144-152.

[18] DAVENPORT A G. Past，present and future of wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics，2002，90（12-15）：1371-1380.

[19] CLOUGH R W，PENZIEN J. Dynamics of structures[M]. 2nd ed. New York：McGraw Hill，1993.

[20] LIEVENS K，LOMBAERT G，VAN NIMMEN K，et al. Robust vibration serviceability assessment of footbridges subjected to pedestrian excitation：strategy and applications[J]. Engineering Structures，2018，171：236-246.

[21] 卢宇杰，程逸建，程正珲，等. 悬挂结构组合楼盖人致振动舒适度试验研究[J]. 建筑结构学报，2020，41（S2）：263-269.

Dynamic responses and equivalent wind load of asymmetric

suspension structure under random wind excitation

LIANG Xiongjie1， YANG Zongwang1， CHEN Min1， ZHANG Lirong2， GE Xinguang*2

（1. China Construction Science and Industry Corporation Ltd.， Shenzhen 518000， China;

2. School of Civil Engineering and Architecture， Liuzhou Institute of Technology， Liuzhou 545616， China）

Abstract： Due to the complexity of dynamic response of asymmetric suspension structure under random wind excitation， a method for analyzing horizontal and vertical coupling vibration response under downwind excitation is proposed. Firstly， the dynamic equations of the asymmetric suspension structure under downwind action are established. The wind vibration equations expressed by generalized coordinates are obtained by the real mode decomposition method， and dynamic vibration parameters are obtained by finite element software. Then， with the complex mode method and the virtual excitation method， the unified frequency-domain solutions of the displacement， velocity and generalized coordinates of the real modes of the suspension structure are obtained. With the quadratic decomposition method， the closed solution of the spectral moment and variance of the above responses and the calculation formula of the equivalent wind force are obtained. Finally， the accuracy of the proposed closed solution is verified by an example analysis， and the effects of generalized coordinates on the dynamic response and equivalent wind force of the asymmetric suspension structure are studied. The results show that the structure will generate both lateral and vertical vibration， and the vertical vibration cannot be ignored under the downwind load.

Key words： asymmetric suspension structure; random wind excitation; closed form solution; equivalent wind load

（责任编辑：罗小芬）

收稿日期：2023-04-07

基金项目：国家自然科学基金项目（51868007）；钢结构装配式建筑复杂结构施工成套技术研究与开发（202207）资助

第一作者：梁雄杰，工程师，研究方向：建筑工程项目管理和技术研发

*通信作者：葛新广，博士，副教授，研究方向：結构振动控制，E-mail：504976454@qq.com