基于滤波器组和小波包变换的超高次谐波检测方法
王江涛,李贻涛,姜 林,周 茉
(1.东北电力大学,吉林 吉林 132012;2.长春华信电力成套设备有限公司,长春 130021;3.华电吉林能源有限公司,长春 130021)
0 引言
随着电力电子技术的发展,越来越多基于电力电子变换技术的新型设备和家庭电力电子设备投入到电力系统的发、输、配、用等各个环节,加之电网中分布式发电和电力载波通信的广泛应用,高频谐波问题引起学者关注[1]。2013年的IEEE PES会议,将频率范围为2~150 k Hz的谐波命名为“Supraharmonics”[2],国内诸多学者也对该频段的谐波进行了命名,本文采用应用最为广泛的“超高次谐波”作为该频段谐波的中文名称。超高次谐波会干扰电力系统中的设备,使设备无法正常工作或损毁,还会干扰电力载波通信,超高次谐波还有可能引发谐振,影响电网正常运行[3]。因此,准确高效地检测超高次谐波的含量、找到超高次谐波源,是治理超高次谐波的前提,也是当前亟待解决的重要问题。
超高次谐波与传统谐波相比具有高频率、宽频域的特点,并且不同超高次谐波源的相互作用更加明显,其传播特性与普通谐波相比更为复杂[4-5]。标准IEC 61000-4-30ElectromagneticCompatibility(EMC)-Part4-30:Testingand MeasurementTechniques-PowerQuality MeasurementMethods中给出了两种超高次谐波的检测方法。一种是将IEC 61000-4-7中200 ms全采样法的检测上限提高到150 k Hz,这种方法虽然能对超高次谐波进行检测,但处理的数据量巨大,对检测设备的要求高,不适用于实际应用。另一种是IEC 61000-4-30附录C中给出的32等距时间窗的检测方法,虽然该方法处理的数据量少,但该方法只利用了8%的数据,可能会遗漏部分信息,检测精度低。为了解决傅里叶变换处理数据量和检测精度的矛盾,国内学者通过改变采样的方式来减少傅里叶变换所处理的数据,并在减少数据量的同时保证检测方法具有较高的频率分辨率[6-7]。还有学者应用压缩感知原理减少检测时所处理的数据量,但该方法以被测信号稀疏性为前提[8-9]。上述方法只能适用于检测平稳信号,而超高次谐波并不总是平稳的,会随基波分量的周期变化而变化,在某些情况下,超高次谐波发射仅限于半个周期的一小部分[10]。所以仅对超高次谐波进行频域分析是远远不够的,还须对其进行时域分析。文献[11]提出一种基于小波包变换(wavelet packet decomposition,WPD)的检测方法,该方法能够同时检测普通谐波和超高次谐波,并且能够对信号进行时域和频域分析。文献[12]提出一种基于下采样的检测方法,该方法利用模拟滤波器将信号进行分段,对分段后的信号用较低采样频率的设备进行采样,减小了采样频率和处理的数据量。
首先,本文利用模拟滤波器组对信号进行分段,分段的目的是将信号频率限制在一定范围内,避免下采样后混叠的信号相互影响;其次,对分段的信号进行采样,减少了采样数据;最后,应用小波包变换对下采样后的信号进行分析。该方法可以有效地减少小波包分解的层数、减小计算量、提高计算速度。
1 模拟滤波器组与下采样
带通采样定理规定,为保证采样后的信号不失真,采样频率须是被采样信号最高频率的2倍以上。由于超高次谐波的最高频率为150 k Hz,所以要使用300 k Hz以上采样频率的采样设备对信号进行采样。本文所提方法就是利用带通采样定理,将带通信号变换为基带信号,有时也被称作下采样。对于原始信号并不是用采样设备直接对其采样,而是先使用模拟滤波器组将信号分成10段,每段带宽为16 k Hz(第一段为14 k Hz,最后一段为6 k Hz),按照带通采样定理就可以用较低采样频率的设备对这10段带通信号进行采样。选用的滤波器是具有椭圆特性的模拟滤波器,滤波器组结构见图1,10个滤波器的通带特性见图2。
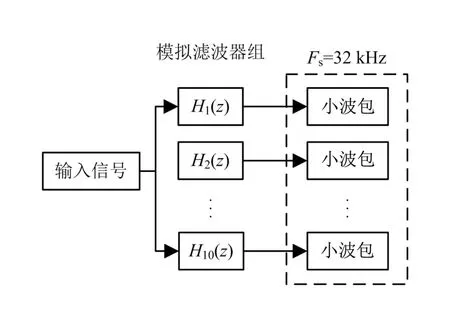
图1 滤波器组结构
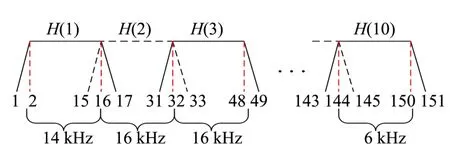
图2 滤波器组幅频特性
采样前的过程都是通过硬件实现,所以该过程并不会增加检测时间。新的采样频率是32 k Hz,采样过程经过了下采样,对于最终的结果要进行如下修正:滤波器序号为偶数时,用式(1)修正,滤波器序号为奇数时,用式(2)修正。
式中:F为修正后的值,即实际频率;f为32 k Hz采样频率下检测的结果,是归一化后的值,其大小为0~1;N为滤波器序号,N的取值为1~10;Fs为采样频率。
2 基于滤波器组和小波包变换的检测方法
2.1 小波包变换原理
WPD是小波变换的推广,小波变换与WPD均能对非平稳信号进行时频域分析,但小波变换在进行小波分解时只对低频部分进行分解,对高频部分的频率分辨率差。而WPD在分解过程中对高频和低频部分进行相同尺度的分解,高频分量和低频分量具有同样的频率分辨率[13]。图3为一个3层小波包分解过程,其WPD是先对信号做小波包分解,将信号分成高频部分和低频部分,对分解后的信号进行2倍下采样,然后进行下一层分解。图3中H表示高频部分,L表示低频部分;hk为低通滤波器系数;gk为高通滤波器系数。

图3 3层小波包分解过程
小波包的二尺度方程如下:
式中:W2n(t)为尺度函数组成的子空间,W0(t)=φ(t)为尺度函数;W2n+1(t)为小波函数组成的子空间,W1(t)=ψ(t)为小波函数。
MATLAB中给出了一系列小波族,例如db小波族、sym小波族、bior小波族等。上述小波族对超高次谐波信号进行WPD时,混叠现象较为严重,所得结果和实际相差较大。文献[14]应用29阶巴特沃斯滤波器作为小波包分解滤波器,该滤波器能够实现对50次以上谐波的最佳小波包分解。此外使用正交镜像滤波器能够降低混叠现象的影响。为减小混叠现象对检测结果的影响,本文使用29阶巴特沃斯正交镜像滤波器作为对信号进行WPD的分解滤波器。
在进行WPD过程中每一层的步骤都是先用正交镜像滤波器对信号进行高通和低通滤波,然后递归地进行2倍的抽取,在此过程中信号的带宽降低50%、数据量降低50%,即下一层中每个节点的带宽和数据量为上一层的一半。
2.2 基于滤波器组和小波包变频的检测方法
文中提出了一种新的超高次谐波的检测方法,将输入信号通过模拟滤波器组变成10段带通信号,对带通信号用采样频率为32 k Hz的采样设备进行采样,该过程实现了对信号的下采样,可以降低信号的采样频率,最后对这10段32 k Hz采样频率的信号分别进行WPD。该方法可以降低检测过程中所要处理的数据量,减少小波包分解的层数,提高检测的速度。
IEC 61000 4-30标准中建议的超高次谐波检测方法中信号的采样频率为1 024 k Hz。要对一个1 024 k Hz采样频率的信号进行小波包分解得到频率分辨率为250 Hz的结果,就要对信号进行11层分解,共进行2 048次小波包分解。而若要对信号先用模拟滤波器组进行下采样,这样就将采样频率下降为32 k Hz。对32 k Hz采样频率的信号进行小波包分解得到频率分辨率为250 Hz的结果,只须进行6层分解,每一段信号做64次小波包分解,共进行640次小波包分解。该方法的计算次数为原始方法的31.25%,能有效地降低计算量,提高计算速度。
通过对WPD结果做进一步处理与分析可以得到更为精确的结果。对小波包分解最后一层各节点的数据做希尔伯特变换(Hilbert transform,HT),然后求其瞬时频率。这样就可以进一步提高检测结果的精度,使频率误差在100 Hz左右。
式中:Y(t)是任意连续信号X(t)的HT;Z(t)为X(t)和Y(t)组成的解析信号;α(t)为向量Z(t)的幅值;θ(t)为瞬时相位;ω为瞬时频率。
由于小波包分解过程中进行了2倍的下采样,求取瞬时频率后,须对求取的结果进行修正。在小波包分解过程中,若信号通过低通滤波器则用式(9)修正,通过高通滤波器则用式(10)修正。
式中:Fb为所通过滤波器通带宽度的2倍。
本文所提方法的检测步骤:
1)对被采样信号先用模拟滤波器组进行分段,分成10段带通信号,用32 k Hz的采样设备对这10段带通信号进行采样;
2)对采样后的信号进行WPD;
3)将WPD的结果进行H T,求取瞬时频率;
4)对瞬时频率进行修正。
3 算例
为验证所提检测方法的准确性,本文模拟基波频率为50 Hz的低压配电网进行仿真实验,待测电流信号中的基波和超高次谐波分量用式(11)表示。
式中:Ah为设置信号的幅值;fh为设置信号的频率;θh为设置信号的相位。
3.1 平稳信号仿真测试
对10个基波周期的数据进行仿真分析。对被测信号分别用采样频率为1 024 k Hz和32 k Hz的采样设备进行采样。对1 024 k Hz采样频率的信号直接进行WPD。使用采样频率为32 k Hz采样设备对被测信号进行采样前,先用10组高通和低通滤波器组成的带通滤波器将信号分为10段带通信号,再对这10段带通信号进行采样。对这10段32 k Hz采样频率信号进行小波包分解,对WPD后的结果进行H T求瞬时频率,并用式(9)和式(10)对求得的瞬时频率进行修正。对上述两种检测方法的检测结果进行比较,记录两种方法WPD所需的时间,其检测结果频率和幅值对比见表1。

表1 实验结果
由表1可得,本文提出方法的频率误差的最大值为100 Hz,而传统的小波包算法频率误差的最大值为250 Hz,所以本文所提方法检查结果的频率误差较小;本文检测结果幅值的误差为0.01 A左右,检测结果与传统小波包检测结果相近。应用MATLAB进行仿真实验,仿真过程中11层小包波分解用时0.356 1 s,滤波器组与小波包结合的方法总用时0.090 3 s,其用时约为传统小波包分解的1/4。由此可见应用滤波器组与WPD结合的方法可以有效地减少计算的时间,其分解结果与传统小波包分解结果相近,应用HT求瞬时功率可将频率误差最大值由原先的250 Hz减小为100 Hz。
3.2 非平稳信号仿真测试
为了模拟某些超高次谐波分量的动态特性,验证文中所提方法可以对该类具有动态特性的超高次谐波分量进行检测,构建如下非平稳信号进行验证,检测结果见图4。
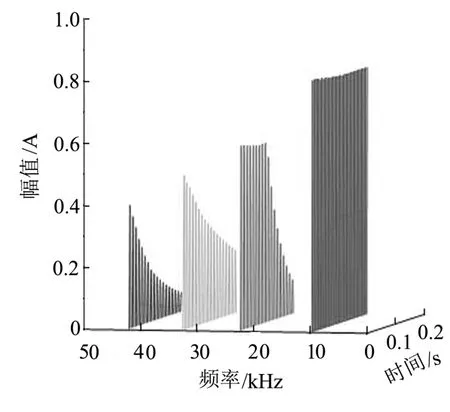
图4 检测结果
由图4可知,仿真电流信号中频率为10.2 k Hz的超高次谐波分量是平稳的,幅值不随时间变化。随着时间的增大,频率为33.1 k Hz和42.9 k Hz超高次谐波分量的幅值随着时间的增长而逐渐衰减,并且42.9 k Hz比33.1 k Hz的超高次谐波分量衰减速度快。频率为23.1 k Hz的超高次谐波分量,在0~0.1 s时幅值不发生衰减,从0.1 s开始幅值随时间增大逐渐衰减,并且衰减速度在3个衰减的超高次谐波分量中最快。仿真结果表明,本文所提方法既可以分析平稳的超高次谐波分量,又可以对具有动态特性的超高次谐波分量进行动态分析。
4 结语
本文针对超高次谐波检测过程中处理的数据量大、检测时间长并且具有非平稳分量的问题,提出来一种基于模拟滤波器组与WPD的超高次谐波检测方法。该方法应用模拟滤波器组对信号进行分段可以降低信号的采样频率,降低对测量仪器的要求,并减少处理的数据量;应用本文方法既可以分析平稳的超高次谐波分量,又可以分析非平稳信号;对WPD结果求取瞬时频率可以进一步减小频率误差。仿真结果和理论分析表明,该方法能够减少小波包分解层数、减少计算量、提高检测的精度与速度。

