产品远程诊断服务的监控质量与定价决策研究

孙明耀 柴强飞 吴 锋

(1. 首都经济贸易大学工商管理学院;2. 南京邮电大学管理学院;3. 西安交通大学管理学院)

1 研究背景

新一代信息技术(如物联网、大数据、信息-物理系统等)与制造业的深度融合,提升了对工业产品的远程监控能力以及基于产品实时状态的维护能力。众多制造业巨头积极部署远程监控平台以提升竞争力,为服务型制造的发展带来了新机遇[1,2]。例如,ASML公司通过部署远程监控平台对其出售的光刻机进行状态诊断,并基于此优化其关键备件库存控制策略;劳斯莱斯对飞机引擎退化状态进行实时监控与分析,并承担引擎的维护、修理以及升级的任务[3,4]。有数据统计显示,远程诊断可以提升20%的生产效率,并使设备的故障率降低50%以上[5]。但是,受限于数据质量等因素,远程诊断服务在现实应用中会出现诊断偏差,严重影响了企业对于维护服务的升级优化。

产品在日常使用过程中由于磨损、环境变化、腐蚀等原因而产生功能退化现象,因此需要及时、精准维护以保障产品的正常使用。远程诊断可以大幅提升产品维护效率、降低维护成本[6]。典型的基于远程诊断的维护服务过程如下:首先,当产品功能退化到一定程度而出现异常时,远程诊断平台提前发出预警;然后,产品专家或专业售后人员对预警数据进行分析,诊断得出产品的故障位置、所需替换的零部件等信息;最后,组织技工到现场,依据专家制定的维护流程,对产品问题进行处理[7]。然而,专家或专业售后人员的诊断结果受预警数据的数据质量影响(后文称监控质量)较大,而导致诊断结果与现实存在偏差。根据ALIZAMIR等[8]以及TOPAN等[3]的研究,诊断偏差包括两类:严重退化诊断为轻微退化(错误Ⅰ)、轻微退化诊断为严重退化(错误Ⅱ)。由于技工维护是依据专家给出的维护指导进行操作,所以诊断结果误差会直接体现在产品的修复效果上,进而对产品用户造成错误成本。

依据上述维护服务过程,服务商可以通过两种方法提升远程诊断的精确度:①增大硬件与软件投资成本(如传感器、网络等),提升监控数据的数据质量(即监控质量)[9];②提高专家的诊断时间,许多诊断服务研究均假设提升诊断时间会提高诊断精度[8,10]。该假设也与现实一致:当专家有更多时间将预警数据与过往的故障数据库进行匹配和对比时,也就更可能准确地定位故障并给出维护方案。但是这两种提升精度的方法均对服务系统有负面影响,前者需要加大投资,后者会造成用户的等待时间增长。因此,远程诊断服务商需要寻求监控质量、投资成本以及用户等待之间的均衡,以最大化自身收益。

相关研究包括两方面:考虑监控质量的维护运营管理决策,以及基于排队论的诊断服务研究。大部分关于远程诊断对企业管理决策的研究,关注维护策略与备件库存策略方面。如TOPAN等[3]以光刻机的维护为例,考虑关键备件替换需求可以通过远程监控平台预测得到,但同时存在多类诊断偏差,基于此对诊断偏差进行建模,并研究了带有偏差的预测信息对备件库存策略的影响。NGUYEN等[11]考虑监控质量是影响基于产品实时状态维护的重要因素,研究了监控质量与基于实时状态维护策略的联合优化问题,并提出一种动态的监控质量与维护方案的调整策略。KURZ[4]以飞机引擎维护为研究对象,考虑远程监控信息以降低需求不确定性并提高维护的服务速率,研究了各个维护站点的能力规划联合优化问题。吴琼等[12]研究了考虑响应时间的制造企业远程监控服务定价策略,但是并未考虑诊断偏差的影响,也未考虑服务系统中用户的排队问题。与上述研究目标不同,本研究从排队系统优化的视角,探讨远程诊断下的维护服务的定价与监控质量联合决策问题,难点在于,如何基于服务商监控质量决策构建诊断误差以及相应错误成本函数,并且诊断误差如何影响远程诊断维护服务系统均衡也值得进一步探究。

关于基于排队论的诊断服务优化问题,WANG等[13]考虑提高护士的专业水平或诊断时间可降低诊断误差,研究了医疗服务系统中护士的专业水平、诊断时间以及护士数量的联合优化问题。ALIZAMIR等[8]假设提高诊断时间可以提高诊断精度,对诊断服务中的两类错误进行建模,研究了诊断服务系统的动态精确度——拥挤度均衡问题。SUN等[10]以售后服务系统为研究对象,在上述研究的基础上,考虑诊断偏差导致的错误成本随着诊断偏差递增的情形,研究了售后服务系统规中诊断专家水平以及诊断时间的联合决策问题。周华等[14,15]研究了专家服务系统下的最优专家水平决策问题以及专业服务的定价问题。孔瑞晓等[16]研究顾客排队对服务商竞争的影响。李武强等[17]研究用户偏好对服务系统速度-均衡的影响。上述研究均考虑诊断精度由专家诊断时间确定,但是在远程诊断服务中,监控质量同样是决定诊断精度的重要因素。当纳入监控质量后,如何构建由监控质量与诊断时间共同确定的诊断精度以及用户错误成本模型,并研究其对排队系统和服务商决策的影响成为挑战。本研究通过构建贝叶斯更新模型,建立诊断误差与错误成本函数,探讨远程监控维护服务系统中用户加入-退出策略以及服务商的决策均衡问题。

基于上述工业实践遇到的问题以及相关理论研究的不足,本研究考虑产品远程诊断中的诊断误差,探讨远程诊断服务商监控质量与服务定价联合决策。假设远程诊断精度由监控质量与专家诊断时间共同确定,服务商可以通过提高监控质量(比如使用更精确的传感器)的方式提高诊断的精度,但同时需要支付更多的投资成本。用户通过权衡远程诊断服务效益、等待成本以及服务价格的大小,决定是否使用该服务。服务商以用户决策为基础,通过确定合适的监控质量以及服务价格以最大化自身利益。本研究通过构建策略性排队模型,主要探讨以下科学问题:①用户对于远程诊断服务的效益应如何表示?②在不同市场环境下,用户的均衡决策是否一致?③服务商关于监控质量与定价的联合决策是怎样的?④专家诊断时间如何影响系统均衡?

2 模型与假设

本研究考虑两类市场主体:产品用户及远程诊断服务商。产品有两种退化状态:严重退化和轻微退化[18]。远程诊断平台收集产品运行数据并由设备专家进行分析,确定产品退化状态后给出解决方案。由于数据质量问题,导致专家的诊断结果存在误差并最终导致用户承担一定的错误成本。本研究考虑监控质量与专家的诊断时间共同决定诊断精度。当监控质量越高且诊断时间越长时,诊断结果越准确,但同时会造成较高的投资成本与用户较长的等待时间。

本研究使用M/M/1队列对系统进行建模,其中诊断时间为τ,用户的潜在需求到达率为Λ,τ与Λ分别服从于指数分布与泊松分布。本研究不考虑无用时间损耗,即诊断时间τ全部被专家应用于确定产品故障与所需维护相关信息。现有关于售后维护服务系统优化的研究中,多采用M/M/1队列进行建模,如SUN等[19]使用M/M/1队列分析ASML公司关于光刻机维护的能力规划问题;KURZ[4]同样使用单服务员队列研究劳斯莱斯飞机引擎维护的能力规划决策,该队列模型不但简化了分析过程以求得问题的解析结构,而且在一定程度上刻画了售后维护服务系统的不确定性。本研究主要变量符号的含义见表1。

表1 主要变量符号的含义

2.1 用户感知效益

每个进入队列的用户,其使用产品状态为严重退化(D)或者轻微退化(d)。对于严重退化的产品,需要大修维护(如部件替换等),将这种服务类型记为“+”;对于轻微退化的产品,需要小修维护(如润滑清理等),将这种服务类型记为“-”。当严重退化产品(D)进行了大修维护(+)或者轻微退化产品(d)进行了小修维护(-),用户不会生产任何额外成本。但是,当严重退化产品(D)采用小修维护(-)时,用户产生错误成本c1(错误Ⅰ),例如维护不足的设备会导致次品的产生,影响企业制造成本及信誉等;当轻微退化产品(d)采用大修维护(+)时,用户的错误成本为c2(错误Ⅱ),例如非必要备件替换成本与停机成本。

令产品状态为D的先验概率为p0。本研究假设固定值先验概率有以下两个原因:①现有应用贝叶斯更新的诊断服务相关研究,如WANG等[13]和ALIZAMIR等[8]均采用固定值先验概率;②在实践中,产品服务商会根据历史数据,统计得到产品严重退化或者轻微退化的概率(固定值)以辅助决策。在产品实际状态为D的条件下,服务商通过远程诊断得出产品所需服务类型为“+”的概率为α;在产品实际状态为d的条件下,通过诊断得出产品所需服务类型为“-”的概率为β,并且α和β均为监控质量q及诊断时间τ的增函数。本研究使用贝叶斯更新对诊断精度进行建模,如果通过诊断得出产品所需服务类型为“+”,则产品状态为D的后验概率为

p1=αp0/(αp0+(1-β)(1-p0));

(1)

如果诊断结果为“-”,则产品状态为D的后验概率为

p2=(1-α)p0/((1-α)p0+β(1-p0))。

(2)

由于本研究的重点是探究监控质量和诊断时间的决策问题,因此假设产品状态为D的先验概率为p0=1/2。该假设简化了本研究的模型并且与现实情形一致,原因是当产品的两种退化状态区别比较模糊时,用户才更可能使用远程诊断服务。如果产品的两种退化状态差别较大,即p0接近于0或1时,用户自身便可识别,而不会去使用该服务。该假设与WANG等[13,20]的结论一致。另外,α与β代表了远程诊断精度,其取决于监控质量q与诊断时间τ,且满足α>1/2,β>1/2,即专家通过诊断降低了产品状态的不确定性,进而有更大的概率制定正确的维护策略。线性更新函数被广泛应用于贝叶斯更新,因为其可以有效地利用结构化方式来解决决策理论框架中的建模和规划任务。所以,本研究假设α=β=1/2+δτq。

本研究将使用与不使用远程诊断服务两种情形下的用户错误成本之差,作为用户对于服务的感知效益,即错误成本结余。为聚焦于远程诊断服务,本研究不考虑在未使用远程诊断时,服务商依据实际经验对产品状态做出判断的情形,即当未使用远程诊断时,错误 Ⅰ 与 Ⅱ 发生的概率均为 1/4,用户的期望等待成本分别为c1/4 和c2/4;当用户使用远程诊断服务时,由贝叶斯更新函数可知,两类错误发生概率分别为 (1-α)/2 和 (1-β)/2,用户的错误成本分别为 (1-α)c1/2 和 (1-β)c1/2。所以,两种情形下用户的错误成本结余可以表示为

(3)

2.2 用户的加入-退出决策

除去价格P外,用户还需要付出一个等待成本。通过权衡感知效益、价格以及等待成本的大小,用户做出加入或退出队列的决策。加入队列的那部分用户形成市场的有效需求λ(≤Λ)。另外,本研究假设用户加入队列的速度小于服务商的服务速度,即λ<τ-1;否则,队列的长度将会无限大。本研究使用M/M/1队列对该服务系统进行建模,所以用户的期望等待时间为W=1/(τ-1-λ),用户的期望等待成本为Cw=cw/(τ-1-λ)。因此,用户的净效益函数为

U(λ;P,q)=V(q)-cw/(τ-1-λ)-P。

(4)

不失一般性,假设用户的保留效用为0。用户都是同质的,在均衡状态下,具有相同的加入概率p(P,q)。如果p(P,q)=0 或 1,则用户的策略为纯策略;否则,用户策略为混合策略。根据SUN等[21]及HU等[22]关于用户选择加入或退出队列的相关研究,本研究确定用户的均衡策略,具体见引理1。

引理1对于给定的价格P与监控质量q,以λ(P,q) 代表效益函数U(λ;P,q)=0的唯一解:λ(P,q)=τ-1-cw/(V(q)-P),则用户的均衡决策为

pe(P,q)=

(5)

均衡状态下的有效需求为λe(P,q)=Λpe(P,q)。

上述均衡状态定义了3种情形:①当U(Λ;P,q)≥0 时,即使所有的潜在用户加入服务,用户的期望净效益仍为正,因此,加入队列是用户的唯一均衡决策;②当U(0;P,q)<0 时,即使其他的用户都选择不加入队列,用户的期望净效益仍为负,因此,不加入队列是用户的唯一均衡决策;③当U(Λ;P,q)<0≤U(λ;P,q)时,用户策略为混合策略,并且选择加入队列的概率为λ(P,q)/Λ。

2.3 监控质量成本

现实中,远程诊断服务的监控质量与其所使用的监控设备(传感器等)及网络设施等具有密切的联系,并且最终取决于服务商搭建远程诊断系统所投入的成本。根据NGUYEN等[11]的研究,监控质量的投资成本可以使用具有正二阶导数的凸函数进行建模,为保证解析解的可分析,本研究使用二次函数对监控质量投资成本进行建模,该假设与实践一致,即投资监控质量的边际成本是不断增加的,因为监控质量越高时,若要继续提升监控质量变得愈发困难。基于此,本研究建立了如下服务商投资成本与监控质量之间的函数关系:

c(q)=kq2/2 ,

(6)

式中,k代表当监控质量提高时投资成本的增加水平。

2.4 监控质量的决策空间

由用户效益函数(5)可知,用户的效益由监控质量、价格及期望等待成本确定。服务商所确定的监控质量q以及价格P必须满足以下要求:①至少有一位用户会进入队列,且该用户所获取的收益大于0,即V(q)-cwτ-P>0;②价格要至少等于服务每位顾客的成本,即P≥c(q)。结合以上两个不等式,可以得到不等式

V(q)-cwτ-c(q)>0 。

(7)

通过求解不等式(7),可以得到监控质量的取值空间:q∈[q1,q2],其中,q1=(δτ(c1+c2)-((δτ(c1+c2))2-2kcwτ)1/2)/(2k),q2=(δτ(c1+c2)+((δτ(c1+c2))2-2kcwτ)1/2)/(2k)。

3 服务商的最优定价策略

3.1 服务商的利润最大化函数

服务商的决策是通过设定监控质量q以及价格P使利润函数最大化。以定理1中用户的均衡策略为基础,建立服务商利润最大化模型:

(8)

式中,P-c(q) 代表服务商从每个加入队列的用户中所获取的期望利润;λe(P,q) 表示在均衡状态下用户的有效到达率。

为处理上述服务商利润最大化问题,分两步进行求解:首先,对于给定的监控质量q,先求解出企业的最优定价策略P(q);然后,在最优定价原则P(q) 下,推导出服务商的最优监控质量决策。

3.2 服务商的最优定价策略

先分析对于给定的监控质量q,服务商的最优定价决策P(q),详见定理1。

定理1对于任意给定的监控质量q,服务商会以如下方式定价,从而实现利润最大化:

P*(q)=

(9)

(10)

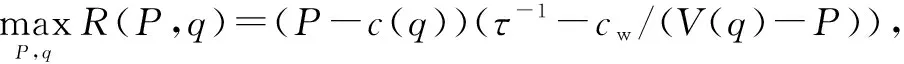
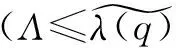
4 最优监控质量决策

4.1 潜在市场需求足够大

当潜在市场需求足够大时,根据定理1,对于给定的监控质量q,服务商的最优定价策略为P*(q)=V(q)-(cwτ(V(q)-c(q)))1/2,相应的均衡到达率为λe(P*(q),q)=τ-1-(cw/(τ(V(q)-c(q))))1/2。将P*(q) 与λe(P*(q),q) 代入服务商的目标函数(9),可以得到

c(q))(τ-1-(cw/(τ(V(q)-c(q))))1/2) 。

(11)

求解上述模型,可以得到在市场需求足够大的情况下服务商的最优决策,具体见定理2。

定理2的证明过程包括两步:首先根据式(11)求取最优监控质量q*,然后将q*分别代入相应价格、均衡到达率与等待时间,可得相应最优解。注意q*=δτ(c1+c2)/(2k) 落入2.4小节中得到的监控质量可行区间之内,即q*∈[q1,q2]。基于定理2,可得到以下推论:

推论1随着诊断时间τ的增大,有以下结论成立:①服务商会提高远程诊断的监控质量q*。②有效需求达到率λe(P*(q*),q*) 先增大后减小。③当用户错误成本相对较高((c1+c2)2≥9kcw/(32δ2))时,最优定价P*(q*) 随τ单调递增;否则,存在区间 (τ1,τ2),当τ∈(τ1,τ2)时,最优价格随着τ的增大而减小,当τ∈(0,τ1)∪(τ2,∞)时,最优价格随着τ的增大而增大。④用户期望等待时间W(P*(q*),q*) 随着τ的增大而增大。

图1 潜在市场需求足够大时服务商的诊断时间对系统均衡的影响

对于均衡需求到达率,当诊断时间处于较低水平(τ<18kcw/(δ(c1+c2))2)时,用户的等待成本较低,因此随着诊断时间增加,用户的错误成本结余增加值要大于等待成本的增加值,进而导致用户的需求不断提高。但是,当诊断时间已经较高(τ≥18kcw/(δ(c1+c2))2)时,等待成本占据了主导地位;当诊断时间增大时,错误成本结余无法弥补等待成本的增大,最终导致用户需求的降低(见图1(b))。

推论1还说明,服务价格未必随着诊断时间以及监控质量的提高而提高。当两类错误成本c1与c2相对投资成本k较高(9kcw/(8(δ(c1+c2))2)≤4)时,最优服务价格随着诊断时间的增大而增大。因为此时相对于服务价格,用户更加关注错误成本,所以服务商可以提高价格以获取所有消费者剩余(见图1(c)中的实线部分)。但是,当错误成本相对来说比较低(9kcw/(8(δ(c1+c2))2)>4)时,服务价格与诊断时间的关系较为复杂。特别地,当诊断时间较低(τ<τ1)时, 最优服务定价随着诊断时间递增,因为此时用户更加关注错误成本;当诊断时间较高(τ>τ2)时,最优服务定价也随诊断时间递增,因为此时诊断精度水平很高,用户愿意支付更高的价格来购买服务;当诊断时间处于上述两种情形之间(τ1<τ<τ2)时,随着诊断时间增大,用户对于等待成本的增加更为敏感,因此服务商必须降低服务价格(见图1(c)中的虚线部分)。随着平均诊断时间的不断提高,用户的期望等待时间也逐步升高(见图1(d))。

推论2随着错误成本c1或c2的增大,服务商将会选择提高监控质量q*并提高服务价格P*, 同时,有效需求到达率λe与用户期望等待时间W也将提高。

推论2表明,当用户的错误成本提高时,服务商会提高监控质量q*来提升用户的错误成本结余,同时,为获取更多消费者剩余,服务商会提高服务定价。上述结论是非常直观的。图1中的数值算例结果也可以支撑上述结论,在图1(a)与图1(c)中,实线代表c1=4,c2=3,虚线代表c1=1,c2=1,可以直观地反映出q*|c1=4,c2=3>q*|c1=1,c2=1,以及P*|c1=4,c2=3>P*|c1=1,c2=1。推论2还表明,尽管服务价格随着错误成本的提高而提高,用户并未因此选择离开队列,反而更多的用户会选择加入。原因是随着错误成本的增大,用户错误成本结余的增加值高于价格的增加值,用户的净效益增大。因此,为获取更多的消费者剩余,服务商将会允许更多的用户进入队列,导致有效需求率以及用户等待时间的增高。图1(b)与图1(c)也证明了上述结果的准确性。

4.2 潜在市场需求有限

当潜在市场需求有限,服务商可以服务所有用户时,根据定理1,对于给定的监控质量q,服务商的最优定价策略为P*(q)=V(q)-cw/(τ-1-Λ),相应的均衡到达率为λe(P*(q),q)=Λ。故式(8)中服务商的利润函数可表示为

(12)

求解上述优化问题,可以得到定理3。

比较定理2与定理3可以发现,当市场潜在需求较大时,服务商的均衡决策不受市场潜在需求的影响;当市场潜在需求有限时,尽管服务商的最优监控质量决策不变,但是服务价格、有效需求及用户期望等待时间均与潜在市场规模相关。由定理2可知,均衡状态下用户的期望等待时间与市场潜在需求无关;但是定理3显示,当市场规模有限时,均衡状态下用户的期望等待时间随着市场规模的增大而增大,因为服务商会满足所有潜在用户的需求。

由定理3可以得到以下推论:

推论3(服务商诊断时间的影响) 随着服务商诊断时间τ的增大,有以下结论成立:①服务商的最优监控质量q*增大;②存在区间 (τ3,τ4),当τ∈(τ3,τ4)时,最优服务定价随着τ的增大而增大,否则,最优服务定价随着τ的增大而减小;③均衡状态下的需求到达率不变,用户期望等待时间提高。

同推论1一样,本研究使用数值算例的形式对推论3中的结论进行分析(见图2)。当市场潜在需求有限时,服务商诊断时间与监控质量依然为互补关系。对于服务定价,当市场潜在需求足够大时,推论1显示,服务定价关于服务商诊断时间的变化,取决于用户错误成本与投资成本的相对大小,即图1(c)中实线与虚线的变化趋势是不同的。当市场潜在需求有限而服务商可以满足所有用户时,推论3显示,服务定价关于服务商诊断时间的变化不依赖于任何其他因素。即图2(c)中实线与虚线的变化趋势一致。原因是当服务商可以满足所有用户的需求时,选择加入是用户唯一均衡决策,即引理1中的情形①,所以服务商在调整价格时,只需考虑维持用户均衡,不需要考虑有效需求的影响。由推论3及图2(c)可知,当诊断时间较低(τ<τ3)时,诊断精确度处于较低水平,服务商必须降低价格来吸引用户选择加入该服务;当诊断时间较高(τ>τ4)时,随着诊断时间的增长,尽管用户的错误成本结余升高,但是其增长幅度无法弥补用户期望等待成本的增长幅度(期望等待时间是凸增长的,见图2(d)),所以服务商也需降低服务价格来维持用户均衡;当诊断时间处于两者之间(τ3<τ<τ4)时,随着诊断时间的增长,用户错误成本结余的增长量高于等待成本增长,服务商可以提高价格以获取更大利润。

图2 潜在市场需求有限时服务商的诊断时间对系统均衡的影响

推论4随着错误成本c1或c2的增大,服务商将会选择提高监控质量q*并提高服务的价格P*,但是有效需求到达率λe与用户期望等待时间W保持不变。

推论4的结果与推论2基本一致,即无论是在潜在市场需求足够大还是有限的情形下,用户错误成本对服务商监控质量以及服务价格的影响是一致的。区别在于,当潜在市场需求足够大时,有效需求到达率以及用户的期望等待时间均与错误成本相关;而当市场需求有限时,推论4的结果表示有效需求到达率和用户期望等待时间与错误成本无关。图2也可以支撑上述结论的正确性。

5 研究拓展

5.1 监控质量与诊断时间存在内生关系

在前文分析中,本研究假设监控质量与诊断时间是相互独立的,原因是监控质量是由远程诊断平台的硬件与软件设施决定(如传感器、传输网络等),是服务商的一项长期规划决策;而诊断时间取决于专家水平、服务商承诺最长停机时间等外部因素,在现实中变动较大。本研究为聚焦远程诊断的监控质量决策,因此假设诊断时间是固定的且独立于外部参数,包括监控质量。本小节考虑如下诊断时间与监控质量的内生关系:当监控质量越高时,对于同一专家而言,其数据处理与分析工作将会越容易,即诊断时间将会减少。因此,这里考虑监控质量与诊断时间的内生关系,探究上述结论在该情境下是否仍然适用。考虑诊断时间与监控质量存在如下函数关系:

τ(q)=τ0(1+a/q),

(13)

c(q))(τ(q)-1-(cw/(τ(q)(V(q)-c(q))))1/2)。

(14)

(15)

5.2 案例分析

本小节使用ASML公司光刻机维护为案例对本研究的理论结果进行应用,相关数据来源于TOPAN等[3]和SUN等[19]的研究。选取上述文献中4类常见故障类型中的两类进行分析,分别用K、J表示。ASML公司已经部署了远程诊断平台来持续监测设备的关键参数(如震动、温度、压力和音频等),并且可以及时预知潜在故障,因此提升了维护效率和备件库存控制水平。但是在实际运营过程中,设备故障以及备件需求信号存在误差,如预警的设备未损坏(多检)以及损坏的设备未能预警(漏检),如前文所述,前者会导致错误Ⅱ维护过量的相关错误成本,而后者会导致错误Ⅰ维护不足的相关错误成本。本研究使用上述文献中因诊断误差导致的库存返回成本作为用户错误成本,并且假设两类错误的错误成本相同,使用出现备件缺货时的惩罚成本作为用户的单位时间等待成本。此外,使用信号的精准度作为该公司现行远程诊断的监控质量,并通过本模型验证是否达到最优。相关参数见表2。

表2 ASML案例数据

令调节参数δ=1,kP=20 000,kW=15 000,使用前文的解析结果,可以推导出不同情境下最优监控质量与定价的决策,然后与该公司现在的预警信号精度进行对比,分析存在的不足。相关数值结果见表3。

表3 基于ASML案例数据的均衡解

针对需求不足情形,对于失效模式K,本案例选取潜在需求为Λ=0.05;对于失效模式J,选取潜在需求为Λ=0.1。由分析结果可知,对于失效模式K,企业的最优监控质量决策为0.857,即对失效模式K的预警准确率需要达到85.7%,而实际上企业关于失效模式K的预警准确率为42%,所以企业应加大关于失效模式K的监控质量投资,比如使用更可靠的传感器或者网络传输质量;而对于失效模式J,结果显示最优监控质量决策为0.679,而实际的预警准确度已达90%,所以企业对失效模式J的监控质量已经足够高,未来应投入更多的精力与财力提升关于失效模式K的预警精确度。

6 结语

考虑产品状态远程诊断精度取决于监控质量与诊断时间,本研究以贝叶斯更新模型为依据构建用户效益函数,确定用户的加入-退出服务决策。基于此,通过构建基于M/M/1队列的策略性排队模型,分别在潜在需求足够大与不足两种情形下,研究服务商关于监控质量与服务定价的决策,并剖析了诊断时间对服务商决策的影响,同时研究了监控质量与服务时间存在内生关系的情形对服务商决策的影响。研究结论如下:①用户的加入-退出决策不但受服务商监控质量与定价决策的影响,而且受潜在需求规模的影响。对于任意给定的服务商监控质量与定价决策,当潜在需求规模足够大时,用户的加入-退出策略为混合策略纳什均衡;当潜在需求规模有限时,用户选择加入为纯策略纳什均衡。②当诊断时间与监控质量相互独立时,在监控质量可行域范围内存在服务商净收益最大化的极大值点,且均衡状态下诊断时间与监控质量为互补关系,即当诊断时间增大时,服务商会提高监控质量;当诊断时间与监控质量存在内生关系(替代关系),即监控质量的提高会降低专家诊断时间时,服务商的净收益随着监控质量递增,且服务商在监控质量可行域上限处获取最大净收益。③当市场潜在需求足够高时,服务商诊断时间对服务价格的影响取决于错误成本与监控质量投资成本之间的关系:当错误成本相对投资成本较高时,服务定价随着诊断时间的增大而增大;当错误成本相对投资成本较低时,服务定价与诊断时间呈现双峰关系;此外,有效需求随诊断时间的增大先增大后减小。但是当市场潜在需求有限时,服务定价与诊断时间呈现双峰关系,不再受错误成本与投资成本关心的影响,有效需求始终等于市场的潜在需求。

本研究的理论贡献主要有:①现有关于远程诊断对企业运营管理影响的研究大多关注库存管理与维护策略方面,而本研究从服务能力规划和服务定价的视角,探讨远程诊断监控对售后服务商运营策略的影响;②本研究将监控质量纳入服务商能力规划决策以及服务供应链优化模型,依据不同市场环境下用户的不同策略,探讨服务供应商决策的异同,弥补了相关研究的不足。本研究的管理启示在于:①对于售后服务用户而言,其是否购买服务的决策不仅受服务商能力规划与定价的影响,同时应注意市场潜在规模的影响;②在不同市场规模下,服务商的定价策略存在较大差异,为保证获取最大收益,服务商在进行定价时应充分考虑错误成本、诊断时间以及监控质量投入成本之间的关系;③在监控质量与诊断时间相关以及互相独立两种情形下,服务商应采取不同方式调整服务质量决策。

本研究还存在一些局限性,后续可展开的研究工作包括:①为简化分析,本研究在应用贝叶斯更新时假设对称状态,即服务商出现两种错误(错误Ⅰ与错误Ⅱ)的概率是相同的,该假设使得本研究可以有效地利用结构化来解决决策理论框架中的建模和规划任务;后续研究可考虑放宽该假设,并研究不对称性对服务商决策的影响。②除错误Ⅰ与错误Ⅱ之外,监控错误还可能有多检、漏检现象,后续研究可以将更多的监控错误纳入到决策中。③服务商相较于用户而言具有信息优势,导致其有动机对产品进行过度维护以获取更高的利益,后续研究可将道德风险考虑引入服务商决策模型中。