不同结构对垫层力学及车轨动力学性能影响研究

摘 要：基于结构力学、车辆-轨道耦合动力学理论，以传统横向沟槽型和新型凸台阵列网孔式轨下垫层为研究载体，对比研究两种垫层结构的力学性能及所形成减振型轨道结构的车轨动力学响应。研究表明，凸台阵列网孔式轨下垫层可以在降低刚度值的同时有效地避免最大应力值增大、应力集中、应力分布不均等情况的发生；与沟槽结构相比，凸台阵列网孔式垫层的对数衰减率及阻尼比相对较大，表明该结构对瞬态冲击有较强的吸能作用，可极大地缓解列车对轨道系統的冲击损伤；两种结构的减振型轨道系统都能保证列车的安全运行，采用凸台阵列网孔式结构的减振型轨道系统可以增大钢轨和轨枕的垂向位移量，减小车轨系统的轮轨垂向力和横向力，有效地保护轨道结构部件，减少相关部门的维护次数。

关键词：轨下垫层；凸台阵列网孔式结构；力学性能；车轨动力学性能

Study on the Impact of Different Structures on Cushion Mechanics

and Car Rail Dynamics Performance

Zhao Feng

（ Vehicle Engineering Department，Baotou Vocational and Technical College，Baotou，Inner Mongolia 014035）

Abstract：Based on structural mechanics，vehicle-rail coupling dynamic theory，taking the under-track cushion of traditional horizontal groove structure and the new raised array mesh structure as the research carrier，the mechanical properties of the two cushion structures and rail dynamics response of the shock absorb orbit are compared here.The research have shown that the under-track cushion of raised array mesh structure can effectively avoid the occurrence of maximum stress value，concentration of stress，and uneven stress distribution while reducing the rigid value.Compared with the groove structure，the number of attenuation rate and damping ratio of the dumpling mesh cushion in the municipal array mesh is relatively large，which indicates that it has a strong energy absorption effect on the transient impact，and can greatly relieve the impact damage of the trains rail system on the rail system.The vibration -reducing track system of the two structures can ensure the safe operation of the train.The vibration -reducing track system of raised array mesh structure can increase the vertical displacement of the rail and the pillow，and reduce vertical and horizontal force of the wheel of the car rail system.The vertical and horizontal force of the track effectively protects the rail structure components and reduces the number of maintenance of relevant departments.

Key words：under-track cushion;raised array mesh structure;mechanical performance;car rail dynamics performance

1 引言

振动与噪声是制约轨道交通快速发展的因素之一，因此铁路、地铁等运营公司采用大量的轨下垫层来缓解列车与其走行基础间的相互作用。练松良等［1］对轨道结构的整体刚度进行了理论性的计算，分析了沟槽尺度的改变对轨下垫层刚度值的影响；韦凯、王丰等［2］以Vossloh300钢轨扣件弹性垫板为研究对象，利用配有温度箱的力学试验机，测试垫板随温度、频率、振幅的黏弹塑性动力特征；蒋丽忠、刘丽丽等［3］开展弹性垫板的平面压缩试验，探究不同截面尺寸、不同厚度对弹性垫板的荷载-位移变化规律； Oregui M等［4］研究了常用轨下弹性垫板刚度特性的影响因素，其中包括几何结构、材料特性、温变、时变等；赵峰、和振兴等［5］以网孔式弹性垫板为研究对象，研究了网孔结构的改变对垫板动静刚度特性的影响；王斌仓、和振兴等［6］研究了填充高阻尼弹性材料网孔式垫板，对该垫板的阻尼特性静刚度特性做了分析，并通过改变填充物上下面的间距来优化垫板的刚度、阻尼特性；赵峰、石广田等［7-8］以网孔式枕下弹性垫板为研究对象，分析垫板刚度阻尼特性，并对计算阻尼比的滞回曲线法和对数衰减率法进行对比研究；白彦博等［9］提出一种空气阻尼网孔式弹性垫板，该垫板利用不同材料的弹性差异，在其弹性单元的空腔中形成主气室和附气室，在气室之间往复流动使其产生阻尼作用；翟志浩等［10］分析网孔式弹性垫板动刚度和阻尼系数的温变特性，并基于车辆-轨道耦合动力学理论，评价网孔式弹性垫板在极寒环境中的适用性；罗震等［11］建立了车辆-轨道耦合动力学模型，分析了轨下弹性垫板的阻尼特性对车辆轨道系统的影响；万迎新等［12］对不同开槽形式的轨下垫板进行动力响应分析，考察列车以不同速度通过曲线段时垫板的动力性能，并通过垫板组合优化，解决曲线段轨下垫板损伤等问题。

为了优化轨下垫层的力学性能及车轨动力学响应，轨下垫层的结构形式多种多样有横向沟槽型、凸台阵列型、填充网孔式等。因此在既有的结构形式上，以凸台阵列型结构和网孔式结构为母体，设计出一种凸台阵列网孔式轨下垫层［18］，该垫层具有承载面小，支撑骨架良好的特点，并且曲线形的蜂窝式轮廓，优化了垫层的应力情况。

以新型凸台阵列网孔式轨下垫层为研究主体，传统横向沟槽型軌下垫层为对比主体，基于结构力学理论，对比研究两种不同结构垫层的刚度、阻尼特性；基于车辆-轨道耦合动力学理论，分析采用沟槽型或凸台阵列网孔式的减振型轨道系统对列车安全性指标、轮轨动力响应指标以及轨道系统动态变形指标的影响。

2 相关计算方法

垫层刚度、阻尼特性对减缓车轨振动响应至关重要。刚度特性是指轨下垫层受外力作用时抵抗变形的特性，由单位变形所需的外力来量度；阻尼特性是指垫层不断衰减车轨振动响应的特性。

2.1 刚度值的计算方法

轨下垫层的刚度主要分静刚度与动刚度，静刚度是指垫层抵抗静态垂向荷载所产生的变形，动刚度是指垫层抵抗动态垂向荷载所产生的变形。依据TB/T 2629-1995《铁路混凝土枕轨下用橡胶垫板技术条件》附录中的垫层刚度试验，轨下垫层的静刚度值由公式（1）所描述。［14］

Kq=Fu-FdXu-Xd（1）

式中：Fd—对轨下垫层施加的下限静态荷载，kN；Fu—对轨下垫层施加的上限静态荷载，kN；Xd—轨下垫层加载至Fd时的垂向位移，mm；Xu—轨下垫层加载至Fu时的垂向位移；Kq—轨下垫层的静刚度值，kN/mm。

2.2 阻尼比的计算方法

轨下垫层的阻尼特性由阻尼比来呈现，阻尼比≈阻尼系数/临界阻尼，阻尼比越大意味着垫层衰减自由振动响应的能力就越强，常用计算方式有对数衰减率法和滞回曲线法。

2.2.1 对数衰减率法

对数衰减率法是根据振动衰减的速度来计算阻尼比的大小，假设将车轨系统视为质量、弹簧和阻尼所组成的机械振动系统，其结构如图1所示。［15］

初始激励偏离平衡位置时所产生的弹簧恢复力和阻尼粘性力分别为 ，其中m为质点质量，o为平衡位置，阻尼器c和弹簧k质量忽略不计，可得质点的弹簧-阻尼振动方程由公式（2）所描述：

mx″+cx′+kx=0（2）

式中c为阻尼器的阻尼系数，k为弹簧的弹性系数，x为质点受初始激励所产生的位移量。

对式（2）两边同时除以质量m，可得公式（3）

x″+2εx′+ω20x=0（3）

式中ω0为无阻尼自由振动系统的固有频率ω0=k/m。

所以

ε=c/2m（4）

ζ=ε/ω0=c/2mk（5）

式中ζ为阻尼比，有阻尼的自由振动方程由公式（6）所描述：

X（t）=Ae-εtcos（ω01-ζ2t+φ）（6）

式中φ为初始相位，A为初始振幅。

受重锤冲击后垫层自由振动衰减波形如图2所示。

阻尼振动是将外部的机械能由阻尼系统转化成其他能量的过程，由公式（6）可推导出阻尼比的计算式由公式（7）所描述：

ζ=124δ24π2+δ2（7）

式中δ对数衰减率，是两个周期间隔为n的波峰幅值Ak与Ak+n之比的自然对数值，由公式（8）所描述。

δ=12lnAkAk+n（8）

2.2.2 滞回曲线法

滞回曲线是力与位移间的回环曲线，所包含的面积为结构阻尼所消耗的功，在振动循环内阻尼所做的功与实际荷载所做的功相等，计算式可由公式（9）来描述，荷载与阻尼力的滞回环曲线如图3、4所示。

SD=ED=πab=πu0（cωu0）（9）

式中SD-荷载滞回环的面积；ED-阻尼力滞回环的面积；u0-曲线位移的最大值；ω-循环荷载的频率；C-阻尼系数。

由阻尼系数可得阻尼比，计算式由公式（10）所描述。

ζ=CCcr=C2mω0C=2mζω0（10）

式中Ccr-临界阻尼；ζ-阻尼比。

将C=2mζω0与ω0=k/m代入公式（9），经过变换，可得阻尼比的计算式由公式（11）所描述。

ζ=ED/2π（ω/ω0）ku20（11）

3 研究对象的力学模型

3.1 传统沟槽型与新型凸台阵列网孔式

传统沟槽型，结合横向沟槽型轨下垫层的应用实际，采用“七上八下”的横向沟槽结构形式，整板长度177mm，宽度147mm，高度11.8mm，横向沟槽间距12mm、宽度为5mm、深度为3mm，横向沟槽型轨下垫层结构如图5所示。

新型凸台阵列网孔式，以凸台阵列结构和网孔式结构为结合本体，构建新型凸台阵列网孔式轨下垫层结构如图6所示，其中关键几何参数网孔外孔径直径（R）为10mm、网孔内孔径直径（r）为7mm、凸台承载面宽度（b）为3mm。该结构由多个相同的单体阵列而成，相邻单体交错排列，整体呈现凸台形，承载面为蜂窝式，内腔为空。

3.2 材料本构模型及边界条件

材料本构模型，轨下垫层均由橡胶材料制成，橡胶材料会使垫层在静态荷载和动态荷载作用下呈现出不同的应力应变关系，因此采用Mooney-Rivlin超弹性本构模型来表征静态下的应力应变关系，采用3阶Prony黏弹性本构模型表征动态下的应力应变关系，超弹性、黏弹性本构模型参数如表1、2所示。［16］

边界条件，轨下垫层是位于弹性扣件与混凝土轨枕之间，故将扣件与轨枕视为刚体，三者间的摩擦接触忽略，并将刚性扣件下表面与垫层的上表面、垫层的下表面与刚性轨枕的上表面采用绑定方式连接，对底部六个自由度进行约束，承载结构如图7所示。

4 不同结构对垫层力学性能的影响

刚度、阻尼特性是表征垫层力学性能的关键参数，两特性的好坏将直接影响轨道系统减振降噪的效果，因此将3.1节的传统横向沟槽型结构与新型凸台阵列网孔式结构为研究载体，对比分析两种不同结构轨下垫层的刚度、阻尼特性。

4.1 刚度特性

依据TB/T 3514-2018《客货共线铁路道岔用橡胶垫板》中的垫层刚度试验，以2kN/s的速度匀速加载至100kN，设定下限静态荷载值（Fd）、上限静态荷载值（Fu）分别为20kN和80kN，位移-荷载响应曲线如图8所示，刚度值和最大应力值（Mises）如表3所示。

图5、表3可知，凸台阵列网孔式结构的位移差量大于横向沟槽型结构，因此当施加相同荷载时，凸台阵列网孔式结构垫层的刚度值较小；从整体结构而言，凸台阵列网孔式结构较为复杂，但其承载面的面积相对较小，在自由扩张面不变的情况下弹性性能较优；凸台阵列网孔式结构的边界轮廓由弧线构成，能够滋生应力集中的区域相对较少，所以该结构的应力集中现象较少，应力分布情况较好。

4.2 阻尼特性

根据文献［7］可知，对数衰减率法和滞回曲线法两种方法所计算出的阻尼比相近，但对数衰减率法在计算过程方面更加快捷，在计算原理方面更加简单易懂，因此采用对数衰减率法来计算两种不同结构垫层的阻尼比。依据TB/T 3561-2020《铁路桥梁黏滞阻尼器和速度锁定器》附录中的冲击荷载性能试验方法，对垫层施加100kN的瞬态荷载，振动衰减时间持续0.06s，要求两波峰间隔周期数n的取值能够使Ak+n的波峰值小于Ak波峰值的50%，故选择衰减曲线的第2波峰值与第5波峰值根据公式（7）、（8）来计算垫层的阻尼比。自由振动衰减曲线如图9所示，阻尼相关参数如表4所示。

图9、表4可知，与沟槽型结构相比，凸台阵列网孔式结构垫层的对数衰减率和阻尼比较大，对数衰减率增大约45.9%，阻尼比增大约45.1%，因此凸台阵列网孔式结构对瞬态荷载所引发的振动响应具有较强的衰减能力，能够有效地吸收列车运行时的冲击动能。

5 不同结构对车轨动力学性能的影响

新型凸台网孔式结构在刚度、阻尼特性方面优于传统横向沟槽型结构，因此对比分析采用两种不同结构轨下垫层的轨道系统对车轨动力学性能的影响。

5.1 车轨耦合动力学模型

根据车辆-轨道耦合的动力学理论，通过有限元分析软件和多体动力学软件，建立车辆-轨道耦合的动力学模型，本文中建立的的车辆模型是多刚体模型，轨道模型是柔性轨道，减振轨道结构及简支箱梁桥是外部導入的柔性体模型。

在车辆-轨道耦合的动力学分析模型中，凭借轮轨之间的相互作用形成一个大系统，如图10所示。车辆在运行过程中由于自身因素和外界因素对轮轨之间的相互作用造成影响，从而导致车辆系统的动态响应。

5.1.2 地铁参数

选用A型地铁作为研究车辆，设定运行速度为80km/h，运行距离为800m（采集数据以中间量为主），A型地铁参数和模型如表5和图11所示。

5.1.3 轨道结构部件

轨道结构是由钢轨、扣件系统、轨下垫层、轨枕及道床等部件组成，各类部件相关参数如表6所示。

5.1.4 轮轨接触关系

轮轨法向力由Herz接触力来描述，轮轨法向力为：

Pj（t）=1GΔZj（t）3/2（j=1-4）（12）

式中G-轮轨接触常数；ΔZj（t）-t时刻第j位轮轨间的弹性压缩量。

轮轨切向力是轮轨接触面间产生相对滑动的摩擦力，即轮轨切向力（摩擦力）：

F=μPj（t）（13）

式中μ-摩擦系数；Pj（t）-法向力［17］。

5.1.5 轨道不平顺

采用德国高干扰谱来模拟仿真地铁运行时的不平顺，轨面不平顺随里程的变化样本如图12所示。

5.2 对列车安全性评价指标的影响

脱轨碰撞是轨道交通中绝对禁止的事件，目前铁路、城轨等相关部门由脱轨系数和轮重减载率来评判列车运行的安全性。

5.2.1 脱轨系数

脱轨系数是指车轮上横向力与垂直力的比值（Q/P），根据TB/T2360-1993《铁道机车动力学性能试验鉴定方法及评定标准》，当脱轨系数（Q/P）≤0.6时为优良，Q/P≤0.8时为良好，Q/P≤0.9时为合格［18］，脱轨系数响应曲线如图13所示。图13可知，两种垫层结构的脱轨系数变化规律基本相近，且任意位移量的脱轨系数均低于0.6，表明两种垫层都可以保障列车的安全运行；凸台阵列网孔式结构脱轨系数的峰值为0.264，横向沟槽型结构的峰值为0.266，凸台阵列网孔式结构脱轨系数的峰值相对较小，更能保障列车安全运行，防止脱轨碰撞事故的发生。

5.2.2 轮重减载率

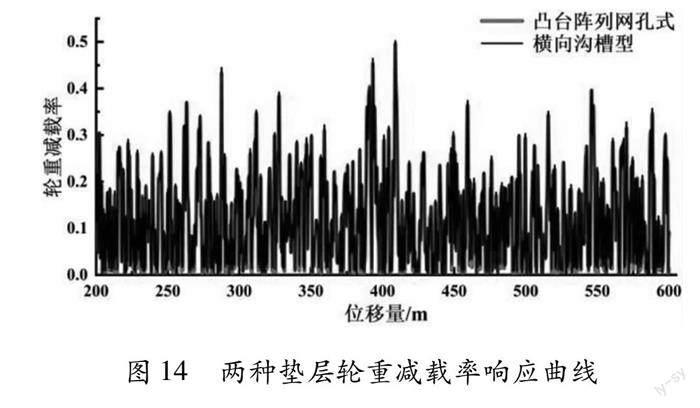
轮重减载率是一种在特定工况下因轮重减载而使列车脱轨的安全性指标，是轮重减载量与平均静轮重的比值（P1/P），根据GB/T14894-2005《城市轨道交通车辆组装后的检查与试验规则》，轮重减载率应≤0.6［19］，轮重减载率响应曲线如图14所示。图14可知，两种垫层结构的轮重减载率变化规律基本相近，且任意位移量的轮重减载率均低于0.6，其中凸台阵列网孔式垫层轮重减载率的峰值为0.4988，横向沟槽型垫层的峰值为0.5040。

5.3 对轮轨动力响应指标的影响

轮轨动力响应会对轨道结构产生不可逆的损伤，其中轮轨垂向力和横向力是用来评价动力响应的两个重要指标。

5.3.1 轮轨垂向力

轮轨垂向力是由轨道的高低不平而引发车轮和钢轨间产生垂向的作用力，主要用于判断轨道的负荷状态，轮轨垂向力响应曲线如图15所示。图15可知，两种垫层轮轨垂向力变化规律基本相近，其中凸台阵列网孔式垫层轮轨垂向力的峰值为72.937kN，横向沟槽型垫层的峰值为73.256kN，表明新型垫层对轮轨垂向力的缓解作用较大。

5.3.2 轮轨横向力

轮轨横向力是由列车的蛇形蠕动而产生的，要求轮轨横向力应≤0.4倍的轴重［20］，轮轨横向力响应曲线如图16所示。图16可知，两种垫层轮轨横向力变化规律基本相近，其中凸台阵列网孔式垫层轮轨横向力的峰值为-13.61kN，横向沟槽型垫层的峰值为13.74kN，由于新型垫层的轮轨横向力较低，可以较好地缓解横向振动响应。

5.4 对轨道系统动态变形指标的影响

轨道系统的动态变形主要是由钢轨垂向位移、横向位移及轨枕垂向位移等变形指标来评判，其中钢轨和轨枕的垂向位移尤为重要。

5.4.1 钢轨垂向位移

钢轨垂向位移量变化曲线如图15所示，由图17可知，图17可知，两种垫层钢轨垂向位移量变化规律基本相近，凸台阵列网孔式垫层钢轨垂向位移量的峰值为-1.904mm，横向沟槽型垫层的峰值为-1.592mm，相较而言新型垫层能够有效地增加钢轨的垂向位移量，提升轨道结构的缓冲效果。

5.4.2 轨枕垂向位移

轨枕垂向位移量变化曲线如图16所示，由图18可知，图18可知，两种垫层轨枕垂向位移量变化规律基本相近，凸台阵列网孔式垫层轨枕垂向位移量的峰值为-0.958mm，横向沟槽型垫层的峰值为-0.660mm，新型垫层的轨枕垂向位移量较大，可加强轨枕对振动响应的衰减效果。

6 结论

基于结构力学和车辆-轨道耦合动力学理论，以新型凸台阵列网孔式和传统横向沟槽型轨下垫层为研究载体，对比分析两种垫层刚度、阻尼特性的差异，并研究分别使用两种垫层结构对车轨动力学性能的影响。

（1）与传统横向沟槽型轨下垫层结構相比，凸台阵列网孔式轨下垫层结构的刚度值和最大应力值（Mises）相对较小，且刚度值的减小并未使最大应力值大幅度的增大，说明该结构轨下垫层可以在降低刚度值的同时更好的维持垫层的应力情况，虽然该结构相对复杂，但更能适用于城轨、重载、高速等弹性性能要求较高的轨道线路。

（2）在阻尼特性方面，凸台阵列网孔式结构轨下垫层的对数衰减率及阻尼比相对较大，对数衰减率增大约45.9%，阻尼比增大约45.1%，表明该结构垫层对于车轨系统所带来的瞬态冲击有较强的吸收能力，能更好地衰减振动响应，缓解列车对轨道系统的冲击损伤，保障列车运行的安全性和稳定性。

（3）无论是采用横向沟槽型或者凸台阵列网孔式结构的减振式轨道系统，任意位移量的脱轨系数与轮重减载率均小于0.6，都能保证列车的安全运行；在轮轨垂向力和横向力方面，凸台阵列网孔式结构垫板与横向沟槽型垫板二者变化趋势与峰值相差不大，凸台阵列网孔式垫板的峰值相对较小，对于缓解垂向和横向的振动响应有一定的优势；与横向沟槽型结构相比，该结构能更好地缓解垂向和横向的振动响应；凸台阵列网孔式结构能有效地增加钢轨与轨枕的垂向位移量，强化对振动响应的缓冲效果，有效地保护了轨道结构部件，减少了相关部门的维护次数。

因此，新型凸台阵列网孔式结构轨下垫层的应用具有一定的可行性，在轨道结构中发展前景广阔。

参考文献：

［1］练松良.轨道结构刚度的理论计算［J］.中国铁道科学， 2004（1）：68-72.

［2］韦凯，王丰，牛澎波等.钢轨扣件弹性垫板的动态黏弹塑性力学试验及理论表征研究［J］.铁道学报，2018，40（12）：115-122.

［3］蒋丽忠，刘丽丽，周旺保等.高速铁路CRTSⅢ型轨道板隔离层关键构件-弹性垫板试验［J］.铁道科学与工程学报，2023，20（1）：1-11.

［4］Oregui M，Man A D，Woldekidan M F，et al.Obtaining Railpad Properties Via Dynamic Mechanical Analysis［J］.Journal of Sound and Vibration，2016，（363）：460-472.

［5］赵峰，和振兴，石广田等.网孔式弹性垫板动静刚度特性研究［J］.机械强度，2020，42（5）：1243-1249.

［6］王斌仓，石广田，和振兴等.填充高阻尼材料增强网孔式橡胶弹性垫板的性能［J］.铁道建筑，2019，59（9）：136-141.

［7］赵峰，石广田，魏晓等.枕下网孔式弹性垫板刚度阻尼特性研究［J］.大连交通大学学报，2021，42（1）：36-42、47.

［8］赵峰.新型枕下弹性垫板及其对车轨系统的动力学影响研究［D］.兰州：兰州交通大学，2020.

［9］白彦博，和振兴，贠剑峰等.空气阻尼对网孔式弹性垫板动力学特性的影响研究［J］.振动与冲击，2022，41（14）：24-32.

［10］翟志浩，和振兴.极寒环境下铁路扣件新型网孔式弹性垫板动力性能及影响研究［J］.中国科学：技术科学，2020，50（2）：235-244.

［11］罗震.高速铁路无砟轨道结构受力及轮轨动力作用分析［D］.成都：西南交通大学，2008.

［12］万迎新，张骞，吕谦和等.某客货共线铁路曲线段轨下装配式垫板动力响应［J］.机械设计，2023，40（4）：28-35.

［13］赵峰，陈学，王斌仓.一种用于降低结构刚度和应力的铁路用弹性垫板［P］.甘肃省：CN209292792U，2019-08-23.

［14］TB/T 2629-1995，铁路混凝土枕轨下用橡胶垫板技术条件［S］.北京：中国铁道出版社，1995.

［15］刘晶波.结构动力学［M］.北京：机械工业出版社，2007：38-78.

［16］卜继玲，黄友剑.轨道车辆橡胶弹性元件设计计算方法［M］.北京：中国铁道出版社，2010：42-51.

［17］翟婉明.车辆-轨道耦合动力学（第四版）［M］.北京：科学出版社，2007.

［18］TB/T 2360-1993，铁道机车动力学性能试验鉴定方法及评定标准［S］.

［19］GB/T 14894-2005，城市轨道交车辆组装后的检査与试验规则［S］.

［20］GB/T 5599-1985，铁道车辆动力学性能评定和试验鉴定规范［S］.

（责任编辑 孙 慧）