基于改进布谷鸟算法的快速充电方法

张宇 徐思

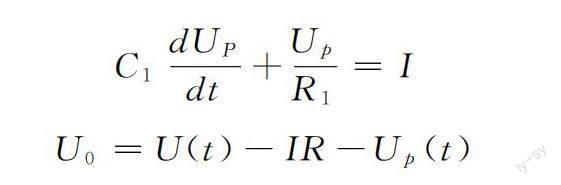
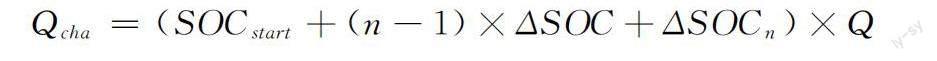
[摘 要]针对锂离子电池快速充电问题，提出了一种基于改进布谷鸟算法的快速充电方法。首先建立锂离子电池等效电路模型和热模型，然后以充电时间和温升为优化目标，采用多阶充电的方法，最后用改进布谷鸟算法搜索每个阶段的充电电流。讨论了充电时间和温升的权重系数对电池充电性能的影响，与传统布谷鸟算法相比，优化布谷鸟算法充电方法能够在温度升高几乎相同的情况下，充电时间减少约5%左右，平衡了充电速度和温升，延长了锂离子电池的使用寿命。

[关键词]锂离子电池；改进布谷鸟算法；充电时间；温升

[中图分类号]TM912.9[文献标识码]A

电动汽车的发展^[1-2]离不开先进的电池技术，如何实现锂离子电池的快速充电也成为当代的热点之一。充电方法对电池确保高质量运行至关重要，充电控制是最重要的因素之一，会影响充电速度、效率、温升，甚至电池寿命^[3]。目前传统的充电方法有恒流充电、恒压充电和分段式恒流恒压充电^[4]。于春梅等^[5]提出了分段恒流结合脉冲充电的方法，能降低电池的极化反应，减少电池充电时间并提高电池的利用效率，但没有考虑充电过程中的温升问题。井子源等^[6]提出基于SOC的充电控制策略，使用充电过程中的温升和能量损耗为指标，通过遗传算法优化每段SOC的充电电流，降低了电池功耗，但在充电过程中SOC分段方式考虑的样本有限。文滨等^[7]提出一种多阶恒流充电和脉冲充电结合的方法，并用模糊控制对充电过程中的充电电流进行控制，该方法在脉冲充电模式中，脉冲占空比的最优化控制不够完善。Zou C等^[8]提出一种优化充电时间的快速充电方法，建立了电池的电化学模型，研究电池的热特性，用先进的控制理论预测充电特性，电池的温升为约束条件，结果证明该方法能在保证安全的情况下减少充电时间。

目前对充电性能增强的研究是在优化充电电流，较少能量损耗、充电时间和温升。在充电期间，电池的特征参数和充电电流限制高度依赖SOC，特征参数在不同的SOC范围内变化。所以本文提出一种多目标充电优化方法，充分考虑了不同SOC阶段的充电限制条件。首先提供了等效电路模型和电池热模型，然后提出一种用于锂离子电池多级充电的多目标充电优化策略，最后分成八个阶段优化充电电流，并比较充电结果。

1 锂离子电池建模

1.1 锂离子电池等效电路模型

对图1使用KCL和KVL得：

式中，U_p为电池极化电压，即为R₁或C₁端电压，I为电池电流，充电时为正，放电时为负。结合上式，解得电池极化电压

可估算出电池在t时刻的OCV。

U_ocv=U_out+IR+U_p

1.2 锂离子电池热模型的建立

建立熱模型用来计算充电期间的温度升高。在本文中，表面温度被认为是电池温度，并且假设是均匀的。电池热平衡方程式可以表示如下：

其中：m表示电池重量;C表示热容量;T_s表示电池的平均表面温度;Q_g表示发出的能量;Q_d表示耗散的能量。发热包含两个部分：不可逆转的发热和可逆的发热。

容量测试包括CCCV充电和CC放电。在25℃时CCCV充电进行充电过程，CC模式的充电电压限制为3.65 V，CV模式的截止电流为0.05 C。放电过程在1 C下进行，直到达到2.5 V。放电容量被视为电池容量。在本文中，C是电池放电1 h的电流速率。电池单元特性参数在每5％SOC间隔时识别，然后在OCV稳定之前静置2 h。考虑到充电之间的滞后效应和放电，本文使用的OCV-SOC曲线为平均OCV-SOC曲线。

2 多目标充电优化方法

2.1 恒流-恒压充电法

电池的充电可以描述成从初始SOC到最终状态SOC的充电过程。传统的CCCV充电模式可以充入大约80%的SOC，该模式可以分为两个阶段（图3），首先电池被恒定的电流预充电至预先设定的截止电压；然后充电模式切换至恒压充电模式，即电池的端电压不变，充电过程一直持续到电流下降到充电时间到达设定的截止时间或者规定的截止电流，达到充电的截止电流需要很长时间。CCCV充电模式简单且易于实现，但该方法不能满足快速充电要求，第二阶段的恒压充电的小电流会大大延长总体充电时间；而且恒流恒压充电并未考虑电池极化效应的影响，充电末期极化效应的加剧会导致充电能量损失增加以及电池温度上升，对电池的充电造成不利影响。所以应考虑并监测电池温度的上升，并根据不同的充电区域调节充电电流以实现快速充电并确保温度在安全范围内。

2.2 优化方法

本文提出一种多阶恒流充电方法，该优化方法具体步骤如下：首先把充电过程中SOC划分为几个阶段，然后把电池的充电时间和温度上升作为目标函数，每个阶段的充电电流的约束由充电电流限制和电池特性的参数决定，再使用改进布谷鸟算法优化每个阶段的充电电流。

把SOC₀到SOC_end划分为n个阶段，在每个阶段都有恒定的电流I₁，I₂，I₃，…，I_n，除了最后阶段是ΔSOC_n，大多数SOC的变化与ΔSOC相同，表达式如下：

ΔSOC_n=SOC_end-（n-1）×ΔSOC_k

每个阶段的充电时间如下：

其中：I_k表示第k阶段的充电电流;Q_k表示第k阶段的电池容量;t_k表示第k阶段的充电时间;Q表示电池容量。

所有充电阶段的总时间

任何阶段每个时间的SOC表达式如下：

其中：k表示第k个充电阶段;n表示第n个采样时间。

充电容量如下所示：

其中：Q_cha表示整个充电过程的电荷质量;SOC_start表示初始状态的SOC。

每个阶段温升总和

2.3 目标函数和约束条件

本文的多阶段充电是要减少充电时间并且控制温度升高。但是有一些充电限制，如充电电流、充电电压和SOC。优化的约束条件如下：

由于充电时期内不同SOC范围的模型参数U，R，R₁和C₁，需考虑不同阶段的充电条件限制，充电电流不应超过电池可使用的最大电流，充电电压不应超过充电阶段的最高电压。对于分段恒流充电而言，首先要把充电的过程分成若干个阶段，以10%SOC为一个充电的阶段，要将10%SOC充到90%SOC需要将充电过程分成8个阶段，每个阶段的充电电流有N种选择，一共有N8种选择，对这些选择都进行寻优算法去处理的计算量太大，通过改进的布谷鸟算法可以更有效的得到最优解。

目标函数可以描述为：

式中：α为充电时间在目标函数中的权重系数;β表示温升在目标函数重点权重系数;t表示充电时间;ΔT表示充电过程中的温升。

将目标函数转换为适应度函数：

适应度范围规定为0，2，式中obj_min为目标函数的最小值，obj_max为目标函数的最小值。目标函数的值越大，适应度就越小，目标函数最小时适应度为2，目标函数最大时适应度为0。电池充电过程中最优的情况是充电时间最小，同时温升最小，所以目标函数越大说明充电效果越差。

3 算法介绍

3.1 布谷鸟（CS）算法的基本原理

布谷鸟选择适合自己鸟巢的方式是随机的，为了模拟布谷鸟的育雏行为，Xin-She Yang和Suash Deb等^[9]提出了以下三条理想规则：

1）每只布谷鸟一次只产一颗蛋，并随机寻找一个鸟巢放置。

2）在随机寻找的鸟巢中，最好的鸟巢会保留到下一代。

3）可利用的寄生鸟巢数量是一定的，宿主鸟能发现外来鸟蛋的概率为p。

布谷鸟使用随机搜索的策略来选择宿主巢，该策略是由Levy航班设计的，这对于解释不同种类生物的食物搜索行为是有用的，Levy Flight模拟随步行其步长由以下方程定义：

levy（λ）≈z^λ

其中z表示飞行长度，λ表示飞行方差。

3.1.1 莱维飞行 布谷鸟按照莱维飞行的方式来寻找鸟窝：

3.1.2 偏好隨机游走 每个布谷鸟蛋都有可能会被鸟窝的主人发现并丢弃，设鸟蛋被发现的概率为p，按偏好随机游走的搜索策略产生新的解：

式中X^t_k和X^t_j表示两个随机解，r～U0，1是缩放因子。

3.2 PID控制

PID控制是指比例、积分、微分控制，PID控制器问世至今已有近70年历史，它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一^[10]。PID控制系统结构见图4。

该算法是将输出的结果经过比例、积分、微分3种运算方式叠加到输入中，从而控制系统的行为。输入e（t）与输出u（t）的关系表达式如下：

其离散形式的表达式如下：

常用的有P、PI、PD和PID控制。

3.3 基于PI控制的改进CS算法

所以基本的CS算法可以看做一个离散的比例控制系统，因为比例控制存在稳态误差，让后期布谷鸟算法收敛的精度不是很好。有学者提出了带权重系数ω的布谷鸟算法^[11]，如下：

该方法取得了良好的效果。为了提高收敛速度，本文提出了一种基于PID控制的布谷鸟算法。在上式中加入了积分，其余不变，表达式如下：

3.4 改进算法的收敛性分析

为了更方便的进行收敛性分析，将PID改进的CS算法近似为一个连续的系统，使用传递函数分析其收敛的条件。

上式等式两边同时减X^t_i有：

连续系统近似表示如下：

设初始条件为0进行拉普拉斯变换得：

系统的开环传递函数：

系统闭环传递函数：

系统的特征方程：

如果让系统稳定并震荡衰减就必须要满足如下条件：

初始条件为0的情况下，输入一个幅度为A的阶跃信号r（t）=A（t），系统稳态误差是：

由此可知：在传统的布谷鸟算法中加入了积分环节之后，系统稳态误差为0，提高了收敛速度和收敛精度（图5、图6）。

为了比较算法的精度，设定最大进化代数为5000并运行30次，比较每个测试函数适应度的均值（AVG）和标准差（STD）如表1所示，可以看出改进布谷鸟精度在所有测试函数中都能获得最优值0，较传统布谷鸟有大幅提高。为了比较算法的收敛速度，将目标函数设置为10^-6并运行30次，比较算法的平均收敛代数（AVG）和标准差（SD）如表2所示，可以看出改进布谷鸟算法较传统布谷鸟收敛速度大幅提升，且达优率（SR）为100%。

4 实验验证

本文选取的LiFePO₄电池的参数如下：电池的额定容量为8 Ah，额定电压为3.2 V，工作电压范围为2.5～3.65 V，最大充电电流倍率为5C。温升和充电时间权重系数为α∶β=5∶5，利用改进布谷鸟算法求得八个阶段的充电电流为39.2，36.6，，29.8，14.3，12.9，11.8，8.5和9.7A。从图7可以看出，文中的温升模型能有效的模拟温度的变化，S1至S8阶段的仿真和测量温度最大相差0.75℃，测量温度最大上升4℃并在1534 s内完成了充电。

S1至S3阶段的SOC值比较小，充电电流很大，测量的温升急剧上升，最大温升达到3.5℃。S4至 S6 阶段的充电电流明显减少，温升相对平稳。S7至S8阶段散热量大于发热量，温升略有下降，但在充电最后阶段因为极化电阻的不稳定性，仿真温度温升明显而测量温度略有下降（图7）。

在本文中有两个目标函数，一个充电时间，一个温升。α代表充电时间的权重系数，β代表温升的权重系数，SOC分段比例为10%，还选取权重比例α∶β=3∶7，α∶β=7∶3进行对比，结果如图8和表3所示。在不同的权重系数下，随着SOC的增加，充电电流的整体趋势逐渐减小。随着α比重增加，充电时间减少，但温升增多。反之充电时间增加，温升减少。从实验结果可以看出，本文提出的方法可以在整个充电阶段优化充电电流，减少了充电时间并控制温升，随着电池的低温升高，还可以有效抑制电池老化。

5 结论

快速充电作为电动汽车的关键技术，控制电池的充电时间和温升是及其重要的。本文提出了一种充电方法来平衡充电时间和温升，以充电时间和温升为目标，提出改进布谷鸟算法，在传统布谷鸟算法中引入PID控制中的积分环节，提高了收敛速度和精度。实验结果表明，所提出的充电方法可以在合理的温度升高的情况下明显减少充电时间，并且权重系数对电池充电性能具有重要影响。

[ 参 考 文 献 ]

[1] 王丽瑶.电动汽车充电技术综述[J].时代农机，2019，46（07）：96-97.

[2] GAO LONG Z. Fast charging lithium batteries： recent progress and future prospects.[J]. Small （Weinheim an der Bergstrasse， Germany）， 2019， 15（15） ： e1805389.

[3] 龚瑞昆，徐广璐.锂离子电池快速充电系统技术研究[J].现代电子技术，2020，43（22）：27-29， 35.

[4] YANG X G， ZHANG G， GE S， ET AL. Fast charging of lithium-ion batteries at all temperatures[J]. Proc Natl Acad Sci U S A. 2018;115（28）：7266-7271.

[5] 叶剑晓，于春梅，梁奇.电动汽车用锂电池快速充电技术研究[J].电气传动，2018，48（06）：93-96.

[6] 井子源. 车用锂离子电池SOC预估及充电控制策略研究[D].长春：吉林大学，2018.

[7] 文滨. 电动汽车充电的智能控制策略及系统集成设计研究[D].长沙：湖南大学，2013.

[8] ZOU CHANGFU， HU XIAOSONG， WEI ZHONGBAO， et al. Electrochemical estimation and control for lithium-ion battery health-aware fast charging[J]. IEEE Transactions on Industrial Electronics， 2018，65（08）：6635-6645.

[9] XIN-SHE YANG， SUASH DEB. Multiobjective cuckoo search for design optimization[J]. Computers and Operations Research， 2013， 40（06） ： 1616-1624.

[10]DABIRI A，MOGHADDAM B P，TENREIRO MACHADO J A.Optimal variable-order fractional PID controllers for dynamical systems[J].Journal of Computational and Applied Mathematics，2018，339：40-48.

[11]周欢，李煜.具有动态惯性权重的布谷鸟搜索算法[J].智能系统学报，2015，10（04）：645-651.

Fast Charging Method based on Improved Cuckoo Algorithm

ZHANG Yu，XU Si

（Hubei Key Laboratory of Solar Energy Efficient Utilization and Energy Storage Operation

Control， Hubei Univ. of Tech.， Wuhan 430068，China）

Abstract：In spite of the current rapid development of electric vehicles， the problem of rapid charging of lithium-ion batteries has become a bottleneck in the application. This paper presents a fast charging method based on an improved cuckoo algorithm. Firstly， the equivalent circuit model and thermal model of lithium-ion battery are established. Then a multi-step charging method is used with charging time and temperature rise as the optimization objectives. Finally， the improved cuckoo algorithm is used to search for the charging current at each stage. The influence of the weighting factors of charging time and temperature rise on the battery charging performance is discussed. Compared to the conventional cuckoo algorithm， the optimised cuckoo algorithm charging method is able to reduce the charging time by around 5% with almost the same temperature rise， balancing the charging speed and temperature rise and extending the life of the Li-ion battery.

Keywords：Lithium-ion battery; improve the cuckoo algorithm; charging time; temperature rise

[責任编校：张岩芳]