基于机会约束的园区综合能源系统优化调度

付波 邓竞成 康毅恒

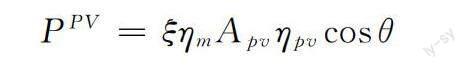
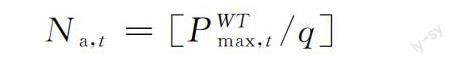
[摘 要]基于机会约束理论应对可再生能源的不确定性，构建了考虑不确定性的园区综合能源系统优化调度模型。同时针对引入机会约束后所建立的隨机优化问题，通过序列运算理论对机会约束进行确定性转化，降低了求解的复杂度，并调用CPLEX对转换后得到的混合整数线性规划模型进行求解。算例仿真验证了该模型和方法的可行性，同时在稳定性和求解速度方面较启发式算法有所提升。

[关键词]机会约束；序列运算；需求响应；园区综合能源系统

[中图分类号]TM73[文献标识码]A

园区综合能源系统根据能源间的互补特性以及能量梯级利用原则，对系统进行协调优化，是提高可再生能源消纳率的重要途径^[1-2]。随着PIES的发展和双碳目标的提出，可再生能源接入比例不断增加，其带来的不确定性为优化调度带来了较大的难度^[3-4]。当下有两种考虑可再生能源不确定性的主流方法：鲁棒优化^[5-6]和随机优化^[7-9]。

相比较而言，采用机会约束方法进行优化调度能取得某特定需求下的最优调度方案^[10-12]。本文提出了一种基于机会约束的PIES优化调度方法。首先，建立各设备模型；其次，利用序列运算方法将可再生能源出力离散为概率性序列；再将含机会约束的调度问题转换为混合整数规划问题（Mixed Integer Linear Programing， MILP）；最后通过YALMIP^[13]调用CPLEX进行求解。通过算例仿真，验证了本文方法的可行性及有效性。

1 园区综合能源系统建模

本文构建的园区综合能源系统（PIES）是电热耦合系统，园区内电能由风机、光伏阵列上级电网供给，热能由电锅炉和储热设备供能。

1.1 风机出力模型

风机出力的不确定性主要来源于风速固有的间歇性、随机性。先前的研究表明，风速服从Weibull分布，风速的概率密度函数

f_w（v）=（k/γ）（v/γ）^k-1exp[-（v/γ）^k]

式中：v为实际风速；k为形状系数，描述了风速概率密度函数的形状；γ为尺度系数，反映了某时段的平均风速，由风速的概率密度函数可以推导出风机出力的概率密度函数。

1.2 光伏出力模型

光伏发电的输出功率主要取决于太阳辐照度、环境温度和组件本身特性等。统计研究显示，一天中的太阳辐照度近似服从Beta分布，光伏输出功率与太阳辐射强度的关系

式中：ξ为太阳辐照强度；η_m为最大功率跟踪点；A_pv为光伏组件辐射面积；η_pv为光伏板能量转换系数；θ为太阳光入射角。光伏输出功率与太阳辐照度呈线性关系，因此光伏输出功率一般也服从Beta分布，可以推导出光伏输出功率的概率密度函数。

1.3 需求响应模型

需求响应利用可控负荷作为灵活性资源参与电力系统的调峰。可时移负荷通过实时调度来实现系统供需平衡，但需确保调节总量不变。可中断负荷是在用户体验尚可的前提下，对负荷功率进行一定削减的柔性负荷。本文需求响应模型描述如下：

式中：P^Load₀为初始负荷；P^Load_t为进行需求响应后的负荷；P^TSL_t为可时移负荷时移功率，δ_TSL为可时移负荷占总负荷比例；P^IT_t为可中断负荷中断功率，δ_IT为可中断负荷占总负荷比例。

2 综合能源系统优化调度模型

2.1 目标函数

接入风电及光伏后，为避免出力偏差带来的能量短缺，需要调用电网及储能作为备用。PIES的运行成本由以下三个部分组成：电网购电成本、备用服务成本、储能折旧成本。

式中：a_t为电网分时电价，P^EV_t为t时段电动汽车消耗的电网电量，P^EB_t为t时段电锅炉的耗电功率，b为电网备用价格，R^grid_t为电网提供的备用容量，c为电储能备用价格，R^ESS_t为电储能提供的备用容量，d为电储能折旧成本，P^ESS_CH，t为t时段电储能充电功率。

2.2 约束条件

2.2.1 系统运行约束

式中：k=EV，grid，EB分别表示电动汽车充放电功率、电网交互功率、电锅炉功率；H^EB_t为电锅炉的供热功率；η_EB为电锅炉电热转换系数。

2.2.2 系统功率平衡约束

式中：E（P_t^DG）为分布式电源出力的期望值；P^GL_t为t时段不可时移负荷，P^Load_t为t时段剩余电负荷；H^Load_t为t段热负荷需求，P^HSS_DC，t为t时段放热功率，P^HSS_CH，t为t时段蓄热功率。

2.2.3 储能约束 本文中涉及的储能设备有电热储能，储能系统能够实现能量的存取，需要确保储能的充放不超过限制，储能系统约束可建模为：

式中：P_CH，t和P_DC，t分別为t时段储能充放电功率，C_t为t时段储能容量，η_ch、η_dc分别为充放效率；式（17）为电储能提供的备用容量约束。

2.2.4 旋转备用约束 本文中通过电储能及电网提供备用服务，表示如下：

式中：P^WT_t、P^PV_t分别为风机及光伏的实际出力。

3 基于序列运算的综合能源系统机会约束优化调度方法

3.1 机会约束的建立

为确保PIES的安全稳定运行，需要向系统内添加系统备用约束。由于备用约束中含可再生能源出力的随机变量，可将其作为随机优化问题建立机会约束。以系统备用容量满足一定置信水平作为约束，出让部分可靠性以降低系统备用需求，所建立的机会约束如下：

式中：P_rob{}为概率计算算子，α为系统置信水平。由于基于机会约束中建立的约束中包含随机变量，模型将无法进行直接求解，通常采用的求解方法为随机模拟法，但该方法需要进行大量的比对运算，降低了模型的求解效率。

3.2 基于序列运算的机会约束确定性转化

3.2.1 序列运算的基本规则 假设有长度为N_a的离散概率性序列a（i）及长度为N_b的离散概率性序列b（i），其有以下几个特征及运算方法：

式中：E（a）为序列a（i）的期望值；⊕为卷和符号；gs₁（i）为卷和运算得到的概率序列。结合电力系统不确定性的实际需求，以风机为例，风机出力的概率序列长度可以通过下式计算：

式中：[]为向下取整，q为离散化步长，P^WT_max，t为t时刻最大出力。风机概率性序列见表1。

光伏出力的概率性序列求取流程同上。由于风光出力的不确定性相互独立，可通过式（3）将风电及光伏出力的序列进行卷和，得到联合出力的概率性序列用于后续求解流程中。

3.2.2 机会约束转换过程 为了将式（2）转换为便于求解的确定性约束，需要提前获取式中随机变量P^WT_t+P^PV_t的分布及其逆函数，当随机变量分离后，可采用解析法进行确定性转换：

式中：φ为随机变量ξ的概率分布函数，φ^-1为φ的逆函数。由式（4）所列形式的概率密度函数形式， 其逆函数难以求解，转换过程中也可能出现非唯一解。本文基于序列对概率分布进行离散化处理，风光联合出力的概率性序列通过卷和运算求得，同时引入0-1辅助变量Zu_a，t，可以将机会约束转化为确定性约束，该变量满足以下两个公式：

式中，σ为数值较大的正数，备用容量大于可再生能源可能的出力变化时，等价于1/σ≤Zu_a，t≤1+1/σ，由于Zu_a，t为0-1变量，此时只能取1；总备用容量小于可再生能源可能的出力变化时，等价于-1/σ≤Zu_a，t≤1-1/σ，此时只能取0，可用式（4）-（6）替代式（1）。至此，含有机会约束的优化调度模型被转化为了MILP模型。

4 算例分析

4.1 算例参数

为验证模型及方法的可行性，以某园区综合能源系统为具体算例进行分析。表2为该园区所接入电网的分时电价；图1为园区可再生能源出力期望值及电热负荷。

电网提供的最大功率500 kW，备用价格0.04元/kWh；风机切入风速3 m/s，额定风速15 m/s，切出风速25 m/s，额定功率300 kW；光伏板能量转化系数0.093，组件辐射面积1200 m²，最大功率110 kW；电储能初始容量32 kW·h，最大容量160 kW·h，充放效率0.9，最大充放功率50 kW，折旧价格0.1元/kWh；热储能最大容量160 kW·h，最大充放功率60 kW；电锅炉功率320 kW，转换系数0.99；电动汽车调度周期内总功率为900 kW。

4.2 PIES最优调度策略

设置离散化步长为10 kW，置信度为90%，求得的调度方案运行成本为2527.52元，调度方案如图2所示。

从图2可以看出，热储能得到了充分的利用，电储能出力较少的原因是用于承担系统备用。同时可以发现，电动汽车充电及向电网购电均集中在低电价时段，提高了PIES系统运行的经济性。此外，系统的弃风弃光功率始终为0，表示可再生能源被PIES系统完全消纳，没有产生弃风弃光现象。

4.3 需求响应对PIES的影响

需求响应具有协调电源及负荷的特性，能够增强对新能源的消纳能力。图3为需求响应前后的负荷变化。从图3中可以看出，需求响应对电负荷曲线有明显的削峰填谷作用，结合分时电价曲线，可以看出调度计划将高电价时段的可时移负荷转移到了低电价时段，提高了PIES的经济性；可中断负荷在中高电价时段中断，进一步提高了PIES的经济性。

4.4 可再生能源不确定性分析

为了验证该方法能够通过人为设定置信水平在可靠性与经济性中达到平衡，选取了5个不同置信水平进行模拟，得到不同置信水平下PIES备用及运行成本（图4、表3）。

图4为不同置信水平下PIES的备用需求，随着置信水平的提高，运行可靠性提高，同时备用增加导致经济性降低；反之，经济性提高，可靠性降低。因此，合适的置信水平能够实现PIES系统在经济性和可靠性间的均衡。