E-预不变凸函数的Hermite-Hadamard型积分不等式及应用
王海英,符祖峰,高景利,虎大力
(南阳师范学院 数学与统计学院,河南 南阳 473061)
1 引言及预备知识
凸性和广义凸性在数学和许多其他自然科学中都发挥着重要作用。当凸函数和广义凸函数应用于这些领域时,它们的积分型不等式通常使其应用成为可能。在这些不等式中,Hermite-Hadamard型积分不等式可能是最常见的一个。设f是[a,b]⊂R上的连续凸函数,则对∀u,v∈[a,b]且u≠v,有经典的Hermite-Hadamard型积分不等式
(1)

近年来,凸函数已得到各种推广。凸函数的一个重要推广是由Hanson[3]引入的不变凸函数。Weir和Mond[4]引入了一类预不变凸函数,并研究了预不变凸函数在最优化、变分不等式和积分不等式中的不同性质和作用。自预不变凸函数的定义提出以后,Hermite-Hadamard型积分不等式与预不变凸函数相结合的研究结果也开始出现。2007年,Aslam[5]建立了预不变凸函数的Hermite-Hadamard型积分不等式
(2)
其中,f是Kη=[v,v+η(u,v)]上的预不变凸函数。
不同广义凸函数的Hermite-Hadamard型积分不等式先后被提出,如文献[8-13]及其里面的参考文献。这些结果极大地拓展了Hermite-Hadamard型积分不等式的应用范围,使得对Hermite-Hadamard型积分不等式的研究更加深入。
Fulga和Preda在文献[14]中引入了下面的E-预不变凸函数的概念,并取得了E-预不变凸函数在数学规划中的一些结果。
定义1[14]设K⊂R,E:K→R,若∀u,v∈K,有
E(v)+λη(E(u),E(v))∈K,∀λ∈[0,1],
则称K是关于η:K×K→R的E-不变凸集。
定义2[14]设K⊂R是关于η:K×K→R的非空E-不变凸集,f:K→R,若∀u,v∈K,有
f(E(v)+λη(E(u),E(v)))≤λf(E(u))+(1-λ)f(E(v)),∀λ∈[0,1],
则称f:K→R是关于η:K×K→R的E-预不变凸函数。
定义3设S⊂Rn是关于η:S×S→Rn的非空E-不变凸集,对∀u,v∈S,定义连接点v和点w=E(v)+tη(E(u),E(v))的η-路径Pvw:
Pvw={E(z)|E(z)=E(v)+tη(E(u),E(v)),t∈[0,1]}。
条件C′[15]对∀u,v∈K,∀λ1,λ2∈[0,1],有
η(E(v)+λ1η(E(u),E(v)),E(v)+λ2η(E(u),E(v)))=(λ1-λ2)η(E(u),E(v)),
(3)
则称η满足条件C′。

2 主要结果
基于函数的E-预不变凸性,首先建立E-预不变凸函数的Hermite-Hadamard型积分不等式。
定理1设K⊂R是关于η:K×K→R的E-不变凸集,u,v∈K且η(E(u),E(v))≠0。若f:K→R是E-预不变凸函数,则有
(4)
证明:因为f:K→R是E-预不变凸函数,对∀t∈[0,1],u,v∈K有
f(E(v)+tη(E(u),E(v)))≤(1-t)f(E(v))+tf(E(u))。
特别地,令t=1/2,得到
对上述两式先分别从0到1进行积分,再进行变量代换,可得
和
整理即可得证不等式(4)。
接下来将利用下面的引理1,对所建立的E-预不变凸函数的Hermite-Hadamard型积分不等式(4)的左右两边的不等式分别进行估计。
引理1设K⊂R是关于η:K×K→R的E-不变凸集,f:K→R可微,u,v∈K且η(E(u),E(v))≠0。若f′∈L(E(v),E(v)+η(E(u),E(v))),则有

(5)
和

(6)

证明:应用分部积分法和变量代换,可得

整理即可得证等式(5)。同理,等式(6)亦可证得。

(7)
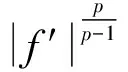

定理3设K⊂R是关于η:K×K→R的E-不变凸集,f:K→R可微,u,v∈K且η(E(u),E(v))≠0,f′∈L(E(v),E(v)+η(E(u),E(v)))。若|f′|q(q≥1)为(E(v),E(v)+η(E(u),E(v)))上的E-预不变凸函数,则有
(8)
证明:由(5)式,|f′|q的E-预不变凸性和幂平均不等式,得到

当q=1时,定理3退化为推论1。
推论1设K⊂R是关于η:K×K→R的E-不变凸集,f:K→R可微,u,v∈K且η(E(u),E(v))≠0,f′∈L(E(v),E(v)+η(E(u),E(v)))。若|f′|为(E(v),E(v)+η(E(u),E(v)))上的E-预不变凸函数,则有
(9)
利用等式(6),类似于定理2和定理3,我们可得到不等式(4)的右边估计值,得到定理4。

(10)
定理5设K⊂R是关于η:K×K→R的E-不变凸集,f:K→R可微,u,v∈K且η(E(u),E(v))≠0,f′∈L(E(v),E(v)+η(E(u),E(v)))。若|f′|q(q≥1)为(E(v),E(v)+η(E(u),E(v)))上的E-预不变凸函数,则有
(11)
当q=1时,定理5退化为推论2。
推论2设K⊂R是关于η:K×K→R的E-不变凸集,f:K→R可微,u,v∈K且η(E(u),E(v))≠0,f′∈L(E(v),E(v)+η(E(u),E(v)))。若|f′|为(E(v),E(v)+η(E(u),E(v)))上的E-预不变凸函数,则有
(12)
接着,我们将所建立的E-预不变凸函数的Hermite-Hadamard型不等式推广到多元E-预不变凸函数情形。
定理6设S⊂Rn是关于η:S×S→Rn的E-不变凸集。假设η满足条件C′。对∀u,v∈S,f:S→R+是η-路径Pvw上的E-预不变凸函数,则∀a,b∈[0,1]且a (13) 证明:设∀u,v∈S,a,b∈[0,1]且a φ(t):=f(E(v)+tη(E(u),E(v))). 因为f是η-路径Pvw上的E-预不变凸函数,由文献[10,定理2]知,φ:[0,1]→R+是[0,1]上的凸函数。令 显然,∀t∈[0,1],有 φ′(t)=φ(t):=f(E(v)+tη(E(u),E(v)))≥0。 从而|φ′(t)|=φ′(t)。由(9)式,得 根据φ的定义,整理即可得证不等式(13)。 定理7设S⊂Rn是关于η:S×S→Rn的E-不变凸集。假设η满足条件C′,对∀u,v∈S,f:S→R+是η-路径Pvw上的E-预不变凸函数,则∀a,b∈[0,1]且a (14) 证明:设∀u,v∈S,a,b∈[0,1]且a 根据φ的定义,整理即可得证不等式(14)。 在本节中,我们回顾以下特殊均值。 性质1令0 (15) 证明:定理1中,令f(x)=x,E(x)=x(x>0),即可直接得证。 性质2令x,y∈(0,1],x Ln(E(y)+η(E(x),E(y)))。 (16) 证明:定理1中,令f(x)=-Lnx,E(x)=x(x>0),即可直接得证。 性质3令x,y∈R,x (17) 和 (18) 证明:定理3和定理5中,令E(x)=x,η(E(x),E(y))=x-y,f(x)=xn,x,y∈R,n∈Z,n≥2,即可直接得证。 推论3令(17)和(18)中q=1,n≥2,则有 (19) 和 (20) 证明:推论1和推论2中,令E(x)=x,η(E(x),E(y))=x-y,f(x)=xn,x,y∈R,n∈Z,n≥2,即可直接得证。 (21) 和 (22) 证明:定理2和定理4中,令E(x)=x,η(E(x),E(y))=x-y,f(x)=xn,x,y∈R,n∈Z,n≥2,即可直接得证。
3 应用


