带有Chaplygin 压力的耦合Aw-Rascle 模型黎曼解的极限∗

翁莎莎，潘丽君†，吕顺

(1. 南京航空航天大学数学学院，江苏南京 211106；2. 工业和信息化部飞行器数学建模和高性能计算重点实验室（NUAA），江苏南京 211106)

0 引言

考虑CAR 交通模型[1]

和

其中：ρ≥0 和v≥0 分别表示车辆的密度和速度，变量u表示相对速度. 压力项p(ρ)是关于ρ的函数，用来模拟驾驶员对前方交通状况的应急反应. 系数η和µ是p(ρ)的比例系数且η>µ>0. 由于密度ρ随着系数的减小而增大，CAR 模型(1)和(2)可以用来表示司机的注意力暂时分散，它们常用来描述司机在驾驶过程中短暂走神的交通现象. 更多关于耦合模型的相关结果见文献[2-4].

2011 年，Herty 等[1]研究了初值为

的黎曼问题，其中常数v-、ρ-、v+、ρ+≥0，压力项满足

他们证明了解的存在性，但解不唯一也不稳定. 潘丽君等构造了具有Chaplygin 压力的CAR 模型(1)和(2)的黎曼解，并证明了解的存在唯一性，其中Chaplygin 压力满足

潘丽君等认为Chaplygin 压力具有负压，delta 激波会出现在上述黎曼问题的解中. 更多关于Chaplygin 压力在交通流模型及其它模型中的应用见文献[5-10].

当µ=η时，CAR 模型转变成经典的Aw-Rascle (AR)模型[11]

当µ=η=0 时，即两侧压力均消失，CAR 模型转变成无压气体动力(PGD)模型

2010 年，Shen 等[12]讨论了压力项为p(ρ)=ργ的AR 模型(5)、(3)的极限，发现当η→0，AR 模型的delta激波解不收敛到PGD 模型(6)、(3)的delta 激波解，不同之处在于delta 激波解的权重和速度. 2013 年，Pan等[13]研究了AR 模型(5)、(4)、(3)的极限，证明了当η→0 时，AR 模型的delta 激波解收敛到PGD 模型(6)、(3)的delta 激波解. 很自然地，我们想知道：当µ→0+且η→0+时，CAR 模型(1)、(4)和(2)、(4)的黎曼解是否相应地都收敛于具有相同初值的PGD 模型(6)的黎曼解？特别是出现delta 激波解时，其极限后的权重和速度是否能与PGD 模型的delta 激波解的权重和速度保持一致？

本文研究带有Chaplygin 压力的耦合Aw-Rascle 模型两侧压力同时消失时黎曼解的极限. 由于耦合模型相变两侧的压力系数不同，导致相变两侧模型存在差异，用经典的方法研究耦合模型比较困难. 因此耦合模型的结果很少，关于耦合模型压力消失时渐近性的理论结果更是几乎没有，具有Chaplygin 压力的非耦合模型压力消失时的理论结果见文献[14-15]. 我们讨论当µ→0+且η→0+时，CAR 模型(1)和(2)的极限，发现CAR 模型(1)、(3)、(4)和(2)、(3)、(4)的黎曼解相应地都收敛于PGD 模型(6)、(3)的黎曼解. 与文献[7]的结果不同的是，极限后的delta 激波解的权重和速度与PGD 模型的delta 激波解的权重和速度完全一致.

1 黎曼解

1.1 CAR 模型(1)和(2)的黎曼解

AR 模型(5)的特征值和对应的右特征向量为

因为

所以系统严格双曲且完全线性退化. 可以得到(5)的自相似解(v,ρ)(x,t)=(v,ρ)(ξ)(ξ=x/t)，计算可得常状态解或者稀疏接触间断R为

对于间断解ξ=σ，Rankine-Hugoniot 条件

其中：[ρ]=ρ+-ρ-，[ρv]=ρ+v+-ρ-v-，其它记号类似. 求解方程(10)可以得到接触间断J和压缩接触间断S分别为

根据右状态(v+,ρ+)的值，潘丽君等得到CAR 模型(1)、(3)、(4)的黎曼解为

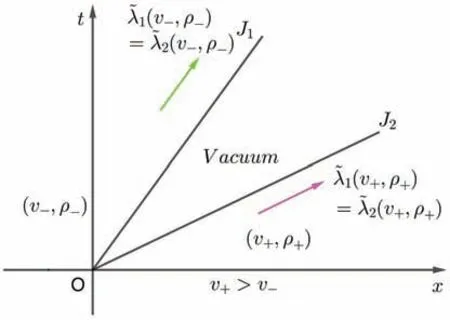
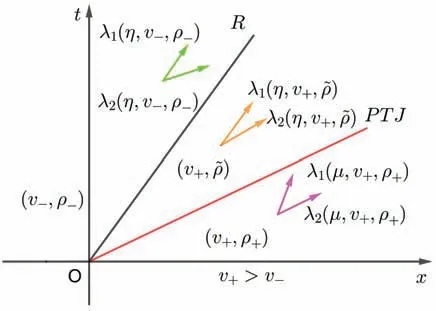
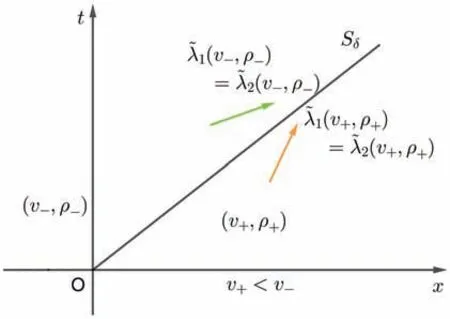
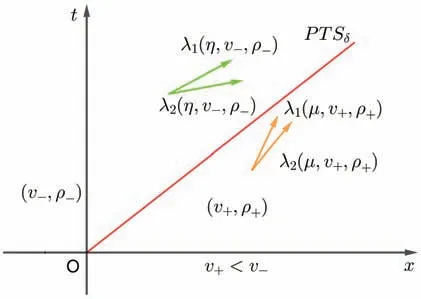
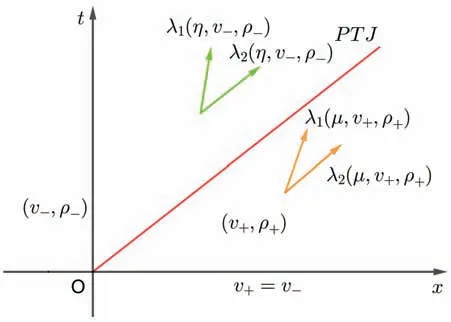
(i) (v+,ρ+)∈I={(v,ρ)|v

(ii) (v+,ρ+)∈II={(v,ρ)|v--(η/ρ-)

(iii) (v+,ρ+)∈III={(v,ρ)|v>v-}:R+PTJ.

其中：“+”意味着“随后”，PTSδ和PTJ分别表示相变与delta 激波重合和相变与接触间断J重合. 相变是指属于不同相的不连续分离状态，即具有质的差异[16]，记作PT. CAR 模型(2)、(3)、(4)的黎曼解为

(i) (v+,ρ+)∈I={(v,ρ)|v

(ii) (v+,ρ+)∈II={(v,ρ)|v--(µ/ρ-)

(iii) (v+,ρ+)∈III={(v,ρ)|v>v-}:R+PTJ.

1.2 PGD 模型(6)的黎曼解

PGD 模型(6)的特征值和对应的右特征向量为

因为

所以系统线性退化. 类似上一小节的讨论，我们可以得到PGD 模型(6)、(3)的黎曼解为

(i) (v+,ρ+)∈I={(v,ρ)|v

(ii) (v+,ρ+)∈II={(v,ρ)|v>v-}:J1+J2;

(iii) (v+,ρ+)∈III={(v,ρ)|v=v-}:J.

2 两侧压力消失时黎曼解的极限

本节我们分别讨论CAR 模型(1)和(2)两侧压力同时消失时黎曼解的极限，并研究该极限与具有相同初值的PGD 模型的黎曼解的关系.根据v+与v-的大小关系，我们将分为以下三种情形讨论：(1)v+>v-；(2)v+

定义1若对任意都满足

则(v,ρ)是黎曼问题(1)、(4)、(3)的弱解.

命题1当v+>v-时，令µ→0+且η→0+，CAR 模型(1)、(3)、(4)和(2)、(3)、(4)的黎曼解都收敛到PGD模型(6)、(3)的黎曼解(如图1 所示)

图1 PGD 模型（6）的黎曼解

其中：接触间断J1和J2的速度σ1、σ2分别满足σ1=v-和σ2=v+.

证明当v+>v-时，CAR 模型(1)、(3)、(4)的黎曼解为(如图2 所示)

图2 CAR 模型（1）的黎曼解

和

令µ→0+且η→0+，可以得到

式(19)说明CAR 模型(1)两侧压力同时消失时出现真空状态. 下面证明稀疏接触间断R转变成接触间断J1.R满足熵条件

令µ→0+且η→0+，熵条件(20)变为

而式(21)正是J1满足的熵条件. 进一步，(1)两侧压力同时消失时，相变也消失. 因此，当v+>v-时，CAR 模型(1)、(3)、(4)的黎曼解(16)收敛到PGD 模型(6)、(3)的黎曼解(15).

当v+>v-时，CAR 模型(2)、(3)、(4)的黎曼解为

注1 由命题1 的证明过程，可以观察到稀疏接触间断到接触间断的转化.

引理1当v+

证明由于v+

命题2当v+

图3 PGD 模型（6）的黎曼解

Sδ的位置x(t)、速度vδ(t)和权重ω(t)满足

当[ρ]/=0 时，

当[ρ]=0 时，

证明由于v+

图4 CAR 模型（1）的黎曼解

PTSδ的位置、速度和权重满足

当[ρ]/=0 时，

当[ρ]=0 时，

不失一般性，我们只讨论[ρ]/=0 情形，[ρ]=0 情形类似可证. 令µ→0+且η→0+，不难计算得到：

将黎曼解(26)和(27)代入式(14)的第一个方程，可以得到

由最后一个等式得到

类似的，代入式(14)的第二个方程，有

由最后一个等式得到

方程(29)和(30)表示黎曼解(23)的广义Rankine-Hugoniot 条件[17-18]成立，即当µ→0+且η→0+时，式(26)的极限是式(23). 下面证明极限后的熵条件成立，PTSδ的熵条件为

令µ→0+且η→0+，熵条件(31)变为

而式(32)正是Sδ满足的熵条件. 因此，当v+

当v+

类似上面讨论，可以证明黎曼解(33)也收敛到PGD 模型(6)、(3)的黎曼解(23).

命题3当v+=v-时，令µ→0+且η→0+，CAR 模型(1)、(3)、(4)和(2)、(3)、(4)的黎曼解都收敛到PGD模型(6)、(3)的黎曼解(如图5 所示)

图5 PGD 模型（6）的黎曼解

其中J的速度为σ=v+.

证明当v+=v-时，CAR 模型(1)、(3)、(4)黎曼解为(如图6 所示)

图6 CAR 模型（1）的黎曼解

其中PTJ的速度为=v+. 很显然，当v+=v-时，CAR 模型(1)、(3)、(4)的黎曼解(35)收敛到PGD 模型(6)、(3)的黎曼解(34)；当v+=v-时，CAR 模型(2)、(3)、(4)的黎曼解

也收敛到PGD 模型(6)、(3)的黎曼解(34).

结合命题1∼3，得到本文主要结果定理1.

定理1当两侧压力消失时，即µ→0+且η→0+时，带有Chaplygin 压力(4)的CAR 模型(1)和(2)的黎曼解都收敛到具有相同初值的PGD 模型(6)的黎曼解.