数学文化对小学生数学核心素养发展作用测评模型构建与实证研究

蒲 淑 萍

(1.重庆师范大学 初等教育学院;2. 重庆市儿童发展与教师教育研究中心,重庆 400700)

突出数学等自然科学的文化价值,是当下中小学数学教育教学的重要目标追求之一。一般来说,数学文化是指数学知识、数学精神、数学思想、数学方法、思维方式等传播文明的总和。而以发展学生关键能力与必备品格的学科核心素养,是当下世界各国教育目标的一致追求与重点关注。数学文化助力于数学教育、教学,学生认知、情感、品格等的发展,其对数学核心素养的提升具有重要意义。然而,数学文化在哪些层面、何种程度影响了学生数学核心素养的发展?我们需要理论探索,更需要走进教学实践,深入分析与探究。当前不少学者对此的认识多停留在思辨分析与实践总结阶段,如林伟[1]、张春辉[2]等人的研究仅停留在对意义和策略的思辨层面,缺乏深入的实证探究与理论概括与总结。这在很大程度上也制约了基于数学文化的中小学数学教育教学的深入开展。鉴于此,本研究将定量和定性相结合,尝试构建数学文化对小学生数学核心素养发展作用的指标体系与测评模型,为不同方式教学对数学核心素养的发展提供借鉴和测评工具支持。

一、数学文化对学生数学核心素养发展作用的内涵与价值

厘清数学文化对学生数学核心素养发展作用的维度,是构建测评指标体系的逻辑起点。为此,研究者通过文献分析等,尝试阐明和廓清数学文化对发展学生数学核心素养作用的内涵意蕴与价值表征。

(一)数学文化对小学生数学核心素养发展作用的内涵意蕴

2017年我国普通高中数学课程标准给出了对数学文化的定义:“数学文化是指数学的思想、精神、语言、方法、观点,以及它们的形成和发展;还包括数学在人类生活、科学技术、社会发展中的贡献和意义,以及与数学相关的人文活动。”[3]10自此,学界对数学文化的内涵有了较为统一、清晰的认识。《普通高中数学课程标准(2017 年版2020修订)》对数学核心素养也给出了明确的界定,“是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的。”[4]4,104-106《义务教育数学课程标准(2022年版)》以核心素养导向的课程总目标概括为“三会”。通过数学学习,学生能获得适应未来生活和进一步发展所必需的“四基”和“四能”,养成对数学良好的“情感态度价值观”[5]5-7。

我国课程标准关于数学文化对学生数学核心素养发展作用主要体现在三个方面:价值观念、必备品格和关键能力,三者缺一不可[6]。以此三个维度为基础,研究者进一步梳理其在小学数学教育教学实践中的具体表现形式,形成每一维度下的评价指标,进而开展数学文化的测评研究。

(二)价值观念、必备品格和关键能力的相互关系与价值体现

1.必备品格

首先,品格是个人成长的重要影响因素[7]。品格与能力共同支撑着学科素养的发展,必备品格与关键能力同等重要[8][9]。其次,数学的工具性与人文性可塑造学科品格。朱德全等认为数学教育的人文性价值取向,以数学独有的品性来“化”人,培养学生的理性精神,练就一种数学的头脑与眼光,能“数学地”观察世界[10]。再次,数学学科必备品格具有学科特质。徐文彬认为“数学自有其必备品格”,既具有数学的特性,又必须拥有教育的品格[11]。数学教学三种最需关注的必备品格:求真的品格、坚持的品格、诚信的品格[12]。必备的数学品格是促进儿童发展的重要力量,其核心价值在于培养儿童的理性精神[13]。数学文化融入数学学科教学,可使学生数学意识、理性精神、质疑、批判精神、探索热情、人文精神等方面的品格获得提升。

2.关键能力

目前,普通高中数学课程标准所确立的数学抽象等6个方面的数学学科核心素养,以及对每一个方面给出的3个水平描述,主要就是从关键能力方面提出的。喻平认为高中课程标准给出了每种核心素养的水平划分,但对日常的学习评价没有直接的指导意义,他建立了基于知识的数学核心能力框架[6]。考虑到小学阶段的基础性与发展性,更应从质量内涵出发构建数学文化对关键能力的测评指标。

3.数学情感、价值、观念

运用数学文化于数学教学,它所带有的信念、价值观、组织文化等隐性特征得以潜移默化地影响学生认识。如,原本认为数学是符号公式的集合静态数学观会发生改变,可以看到数学和其他学科一样是一直在发展变化的;原本认为数学是枯燥乏味、缺乏人文情怀的,通过数学文化的融入,学生必然会对数学学科的人文性认识更到位。数学文化着力于体现数学学科、科学的发展特征、人文特征,从而促进学生数学科学的数学观、数学教学观、数学学习观念更科学、客观、正确;对数学的理论与应用价值认识更清晰。通过数学文化教学,促进学生的数学情感——兴趣与信心、动机,以及数学观念——数学观、数学学习观、数学价值观等的发展。

二、数学文化对数学核心素养作用的评价指标与结构模型建构

基于上述分析,参照已有的关于测评模型构建的范式,研究者对数学文化于数学核心素养发展作用的测评模型进行开发研究。研究者将从考察已确定的数学文化对学生数学核心素养发展作用的三个维度出发,确定各个维度下的具体指标及其要义,进而收集、分析指标数据与生成测评模型。

1.数学文化对学生数学核心素养发展作用的评价指标

(1)关于必备品格的测评

目前,关于数学必备品格的测评研究并不多见。关于必备品格的相关研究,多是结合实践教学进行的思辨分析,内容聚焦于必备品格培养的意义、必备品格的内涵与构成、如何培育必备品格等方面。本研究将以此为基础,考察学生在数学学习过程中的数学意识、理性精神、批判、质疑精神和探索精神、人文精神,以及其对学生关键能力的促进作用。

(2)关于关键能力的测评

数学文化促进数学认知发展。在知识上,通过跨学科等,可以更好地建立知识之间的联系,顺利、高效实现迁移,甚至创造;在技能上通过古今方法对比、学科联系等获得拓展与延伸;在思维及思想方法上,明了思维过程,抓住思想起源与发展脉络,掌握思想方法的本质与精髓,获得更多的智慧启迪。以《义务教育数学课程标准(2022年版)》对核心素养的界定为依据,借鉴喻平教授对以知识为基础的数学关键能力的框架[6],本研究构建起数学文化对数学关键能力发展评价框架,详见表1。

表1 数学文化对数学关键能力发展评价框架

(3)关于情感、态度、价值观的测评

美国心理学家马森(Mussen P. H.)指出:“儿童在学校的成绩和成年后的成就,不仅依赖于他们的能力,而且也依赖于他们的动机、态度和对学校及其他成就情境和情绪的反应。”[14]然而,由于情感、态度、价值观念的内隐性、情境性等典型特征,使得测评学生的数学情感、态度、价值观念并不是一件容易的事情。同时,情感、态度、价值观念虽然作为课程目标的一个维度,但对于认知领域的评价,基本上是对知识学习不同结果的评价,即围绕知识学习开展的,与中国目前课程标准中的“知识与技能”“过程与方法”相对应,只是把这两个要素作为认知领域中不同的水平来表述。对于情感领域的评价,是针对非智力因素开展的,与课程标准提出的三维目标中的“情感、态度与价值观”相对应。相比之下,布卢姆对评价目标有清晰的划分,两个目标指向明确,具有实践层面的可操作性,而中国课程标准提出的三维目标,将三者作为一种并列关系却又捆绑在一起,在实践中是难以操作和实现的。

克拉斯沃尔(Krathwohl)关于情感领域的目标分类,依据价值内化(指由外在的学习转化为个人内在的兴趣、态度、价值等心理特质)的程度,从低到高分为5级:接受、反应、价值化、组织、价值与价值体系的性格化。各个级别的具体表现见表2。

表2 克拉斯沃尔(Krathwohl)兴趣、态度、价值的目标分类细目表

Fennema-Sherman数学态度量表是用于研究学生对数学态度的最流行的工具之一。这一量表已被广泛用于评估学生对学习数学的态度。量表有12个项目,并使用5点李克特量表(从“非常不同意”到“非常同意”)来衡量回答[15]。刘晓惠等研究针对“对初中二年级超常与常态儿童学业情感态度的研究,其特点是详细考察学生对于学习课程(特别是数学课程)的情绪感受范围和层次”。他们使用吴武典提供的四项标准化问卷测量,从对数学课程的态度、数学焦虑、学业经验、动机信念等方面进行问卷调查。这对我们进一步完成对于学生更详细的情感态度分析提供了借鉴[16]。

柳笛以小学数学为例,就特质情绪智力如何影响学生的学业成就开展研究。她对326名小学生进行调查,探索特质情绪智力总体及其各维度对计算流畅性、数值运算、数学推理等数学任务的影响。研究结果显示,不同特质情绪智力水平的学生在计算流畅性、数值运算、数学推理这三个任务总均分上都呈现显著差异;“自尊”“自我激励”对计算流畅性具有显著的预测作用,“自尊”“情绪觉知”和“低冲动性”对数值运算具有显著预测力,“自尊”“自我激励”“低冲动性”和“适应性”能有效预测数学推理。为提高学生的学业成就,应从培养学生情绪智力和构建情绪智力干预机制两方面采取措施[17]。

本研究将借鉴上述研究与本研究的密切相关因素,从数学文化对学生情感、态度、价值观念三个维度开展研究,建立具体指标,明确其对应要义。以此为基础进一步构建数学文化对数学核心素养发展作用的测评模型。

2.数学文化对学生数学核心素养发展作用三维度结构模型初建

(1)数学文化对学生数学核心素养发展作用的测评模型假设

基于上述的文献研究结果和实践认识,本研究提出数学文化对小学生数学核心素养发展作用的测评模型假设:数学文化对小学生数学核心素养的发展作用是必备品格、关键能力和情感观念价值的综合体现。我们认为,数学文化对小学生数学核心素养的影响,不仅表现在有意识的数学意识、数学表达,以及理性精神、批判精神、人文精神等数学必备品格方面;也表现在学生对知识的理解、迁移与创新方面;更表现在学生的情感、数学观、数学价值等方面的认识上。因此,本研究在构建该测评模型时,需从必备品格、关键能力和情感观念价值等因素进行考量。

(2)三个维度及其具体指标、要义

为了更具操作性,我们对数学必备品格分解为四个具体指标:数学意识、理性精神、批判精神、人文精神四个方面;数学关键能力分为三个具体指标:知识理解、知识迁移、知识创新;数学情感观念价值分为数学情感、数学观念、数学价值,形成数学文化对核心素养发展作用的三维度结构体系(表3)。对各项指标的具体内容与要义描述详见表中。

表3 数学文化对核心素养发展作用的三维度结构

(3)3个维度10个指标组成的结构

图1是三个因素之间的关系图,其中V1-V10分别表示各因素的内容。V1:数学意识;V2:理性精神;V3:批判精神;V4:人文精神;V5:知识理解;V6:知识迁移;V7:知识创新。V8:数学情感;V9:数学价值;V10:数学观念。

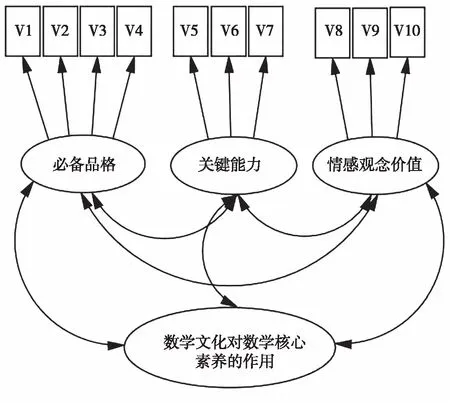
图1 数学文化对数学核心素养发展3维度10因素结构图

这个结构的完全建立,将在作了验证性因素分析后完成。

三、数学文化对数学核心素养发展作用测评模型的验证性分析

对三维度结构模型的探索与验证分析,采用结构方程模型( Structural Equation Model,SEM)方法。验证性因子分析( confirmatory factor analysis)是对社会调查数据进行的一种统计分析,它测试一个因子与相对应的测度项之间的关系是否符合研究者所设计的理论假设。

1.研究设计

根据前文的理论分析,本研究提出两条数学文化对小学生数学核心素养发展的测评模型假设:

假设一:数学文化对小学生数学核心素养发展作用主要体现在必备品格、关键能力与情感态度观念3个维度。

假设二:数学文化对小学生数学核心素养发展作用在品格、能力与价值观念等方面都有不同程度的促进作用。

(1)被试选择

利用一年一度的重庆市数学文化教学比赛和全国小学数学培训工委年会观摩课的准备机会,分别选取四所小学学生共199名(其中A、B两所小学98名学生被试用于探索性因素分析;C、D两所小学101名学生被试用于验证性因素分析)参加调查,其中A小学46名学生(男生25名,女生21名)、B小学52(男生27名,女生25名),C小学53名学生(男生27名,女生26名)、D小学48名学生(男生25名,女生23名)。A、B两所小学收回学生有效问卷98份;C、D两所小学收回学生有效问卷100份,问卷回收有效率分别为100%和99%。

(2)研究工具

自编《数学文化对学生数学核心素养发展作用测评量表》初测版。量表包括3个维度:必备品格、关键能力、情感价值观念。必备品格共12个题项,关键能力12个题项,情感价值观念12个题项,量表最初设计一共36个题项。每个项目均使用利克特(Likert)5点记分法,1表示“很不赞同”,2表示“不赞同”,3表示“不赞同也不反对”;4表示“基本赞同”,5表示“完全赞同”。分别赋值1分、2分、3分、4分、5分,反向题目分别赋值5分、4分、3分、2分、1分。

为了方便项目分析,首先对所有初测数据进行编码和录入。将《数学文化对学生数学核心素养发展作用测评量表》的3个因素的题目依次用Va、Vb、Vc表示,Va维度之下不同项目分别用序号1,2,3,……12表示;Vb维度之下不同项目分别用序号13,14,15……24表示;Vc维度之下不同项目分别用序号25,26……36表示。Va、Vb、Vc题项分布情况见表4。

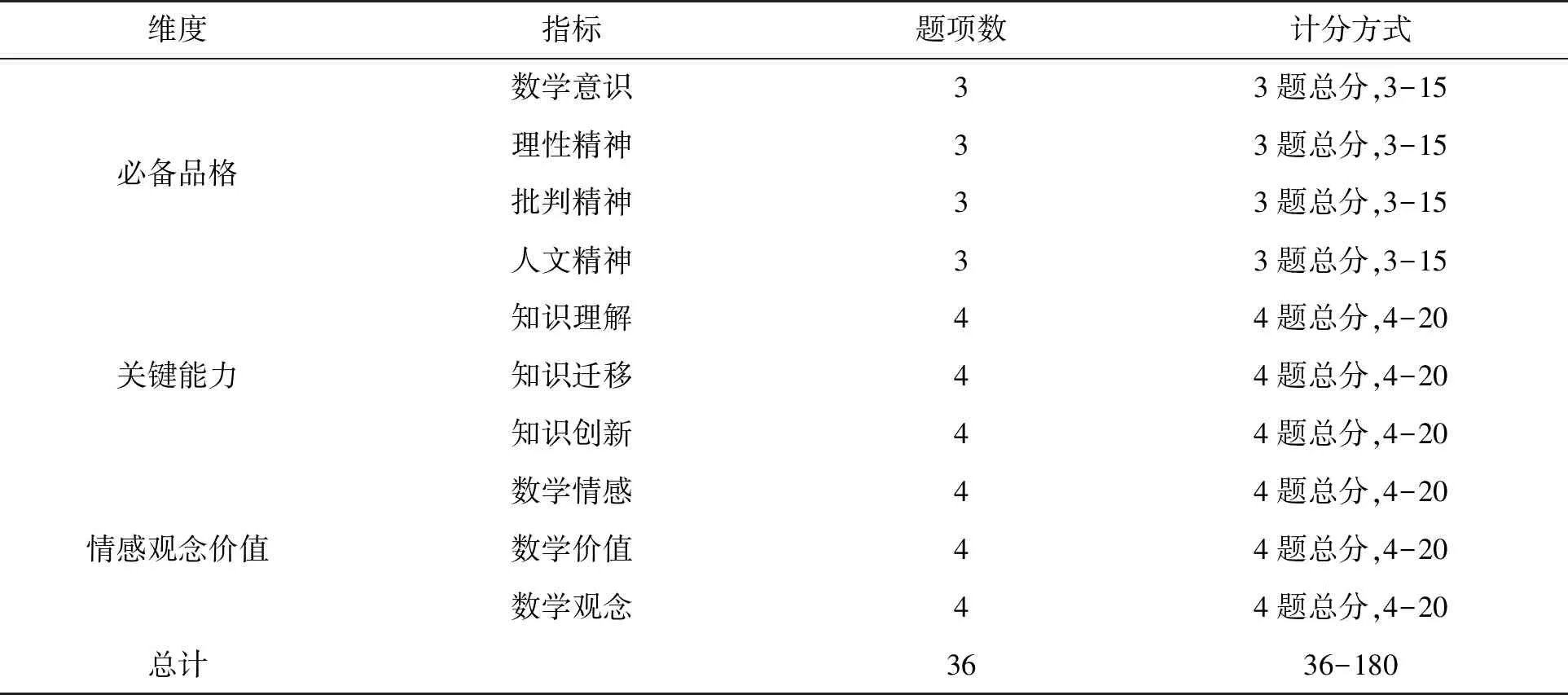
表4 题项分布与计分表

项目选编主要依据已有的相关研究结论以及数学文化对数学核心素养发展作用系统的理论维度。在编制过程中,兼顾必备品格、关键能力、情感价值观念的内容与特点。在项目表述上注意做到语句简单、通俗明了,用词准确。在量表的项目内容上突出体现数学学科以及数学文化的特点,并注意贴合我国小学数学学科教学实际。

项目初步拟定后,邀请重庆师范大学小学数学教育专业的教师和另外一所大学数学教育专业部分研究生评价这些项目。最后综合评价意见,依次对其进行增删或修改。评估的内容主要包括两个方面:一是参照各指标的含义,评价每一个项目是否准确反映了因素的内涵;二是根据量表或量表的语言要求,分析每一个项目的语言表述和可读性,其中特别注意分析题项是否存在歧义,表达是否能够让小学生看懂等。通过对项目的修订,最终确定了《数学文化对学生数学核心素养发展作用测评量表》的初测版。

2.量表结构的数据分析

(1)项目鉴别度分析

项目鉴别度分析的主要考察指标是临界比( critical ratio,CR值)。具体操作方法为按被试数学文化对数学核心素养三维度量表总分排序,取其前、后各27%作为高分组和低分组,然后进行高分组和低分组在各项目上分数差异的独立样本T检验,如项目的CR值达到显著性水平(p<0.05),表明此项目能较好地鉴别不同被试的反应程度。同时,本研究还对题项与量表总分进行相关分析,若题项与量表总分的相关没有达到显著性水平(即p<0.05),表明此题项须剔除。使用上述两种分析方法,删掉不合适的项目共10个。分别是:3,5,8,9,12;15,16 ,19;25,29,31。量表中余下26个题目(见表5)。

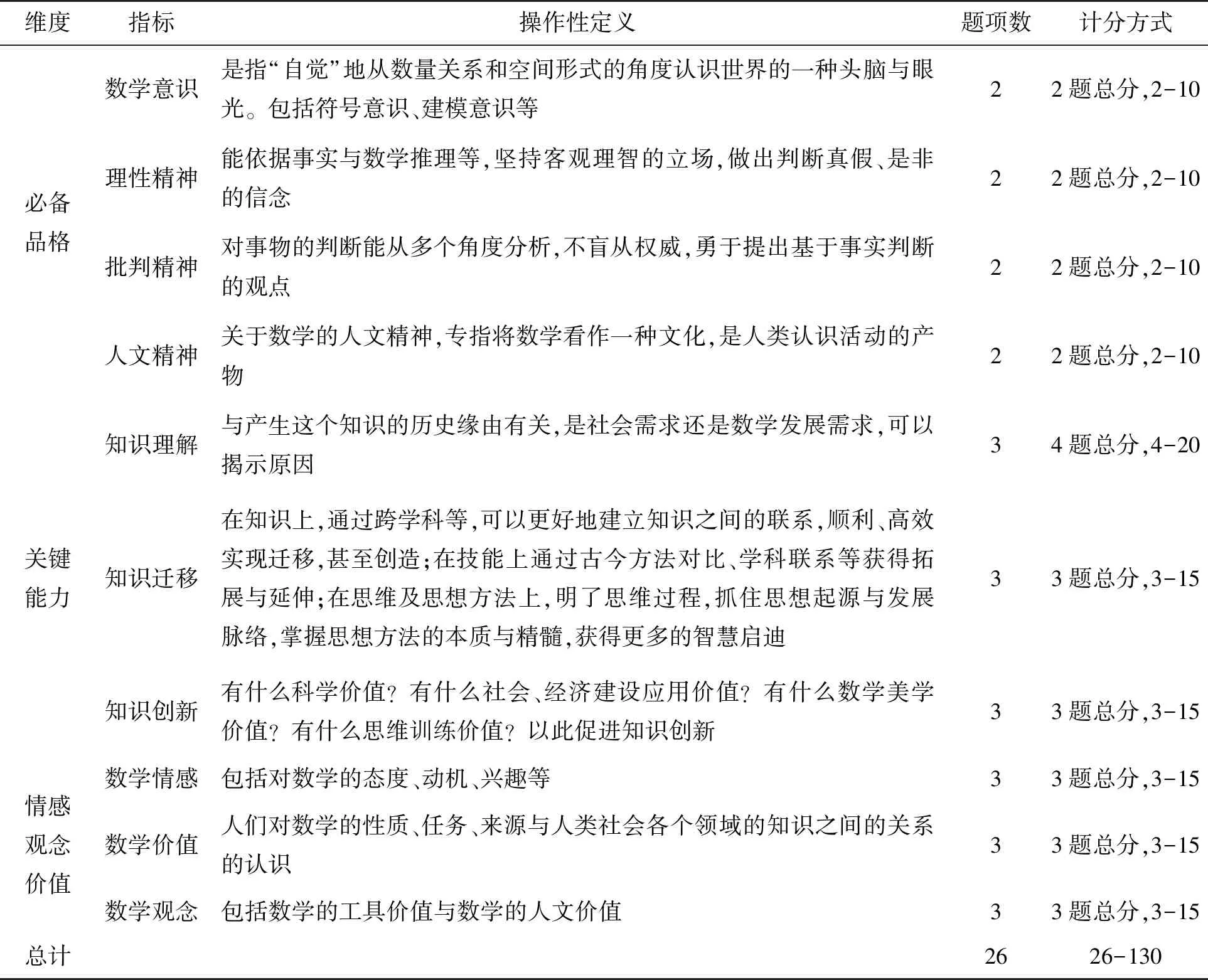
表5 修正后量表的题项分布与计分表

将经项目鉴别度分析、修改后的初测项目编排成量表,请重庆师范大学初等教育学院附属小学10名小学生和5名小学数学教师对量表初稿的适宜性及项目的可读性作出评价并填写可读性评价表。评价表中,对每个项目采用 Likert 5点计分法,其中,1表示“完全明白”、2表示“基本明白、3表示“不确定”、4表示“基本不明白”、5表示“完全不明白”。可读性评估汇总结果表明,10名小学生和5名教师的选择基本集中于“完全明白”和“基本明白”两点,其中“完全明白”占70.3%,“基本明白”占22.7%、“不确定”占6.67%,“基本不明白”占0.33%。对于小学生领会程度较低的项目,作了用词方面的进一步修改。

(2)量表信度分析

信度( reliability)指测量结果(数据)一致性或稳定性的程度。一致性主要反映的是测验内部题目之间的关系,考察测验的各个题目是否测量了相同的内容或特质。稳定性是指用一种测量工具(譬如同一份问卷)对同一群受试者进行不同时间上的重复测量结果间的可靠系数。如果问卷设计合理,重复测量的再次分数间应该高度相关。由于本案例并没有进行多次重复测量,所以主要采用反映内部一致性的指标测量数据的信度。本研究采用了SPSS 19.0分析数据的内部一致性。

《数学文化对学生数学核心素养发展作用测评量表》的信度分析结果见表6。数学文化对学生数学核心素养发展作用系统各维度与指标内部一致性系数为0.698～0.922,总量表内部一致性系数为0.843。可见,数学文化对学生数学核心素养发展作用系统量表的α系数信度指标基本达到了测量学要求,适宜作为测量工具使用。

表6 数学文化对学生核心素养发展作用系统量表信度分析结果( Cronbach’s Alpha系数)

(3)量表效度分析

效度即有效性,它是指测量工具或手段能够准确测出所需测量事物的程度。本研究主要进行《数学文化对学生数学核心素养发展作用测评量表》的内容效度和结构效度分析。

我们对内容效度常采用逻辑分析与统计分析相结合的方法进行评价。本研究是在梳理国内外数学文化对学生数学核心素养发展作用相关研究文献基础上提出来的。理论维度框架的确定综合考虑了它的核心内涵,确定的因素有其坚实的理论基础。项目初步拟定后,请重庆师范大学小学教育专业的教师和另外一所大学部分研究生评价这些项目,并根据他们的意见对题目做了相应的调整。同时,我们还请部分小学教师和小学生对项目的适宜性及可读性进行了评价,对评价结果进行统计分析和进一步访谈,并再次对量表项目进行修改。因此,从整个量表的修编过程来看,《数学文化对学生数学核心素养发展作用测评量表》具有较高的内容效度。

结构效度(construct validity)是指测量结果体现出来的某种结构与测值之间的对应程度。即指测验分数能够说明心理学理论的某种结构或特质的程度。结构效度分析可以采用多种方法来实现。我们主要采用相关系数分析方法检测量表的结构效度。

考察各因素之间的关联性,除了关键能力与情感态度观念达到显著性相关外,其余的组间相关不显著,表明各因素方向一致,但有所差异不可互相替代。四个分量表与总量表之间的相关系数为0.624～0.896,均达到显著性相关水平或非常显著性相关水平,表明各因素与总体概念一致。而且满足分量表与总量表之间的相关,大于各分量表之间的相关。

我们再分别考察每一个子量表之间以及每一个子量表与其分量表的结构效度表7～9的结果。

表7 必备品格各子量表之间的相关及与分量表的相关分析(r)

表8 关键能力各子量表之间的相关及与分量表的相关分析(r)

表9 情感价值观念各子量表之间的相关及与分量表的相关分析(r)

表8～10的结果可以看到,各子量表之间的相关均小于它们与各自的分量表之间的相关,因此,量表有较高的结构效度。

(4)验证性因素分析

研究使用SPSS19.0和Amos19.0对量表进行验证性因素分析。按照我们的理论框架,数学文化对小学生数学核心素养发展作用分为3个维度:必备品格、关键能力、情感价值观念,分别命名为Va,Vb,Vc。必备品格(Va)的观测变量有4个,设为:V1,V2,V3,V4;关键能力(Vb)的观测变量有3个,设为:V5,V6,V7;情感价值观念(Vc)的观测变量有3个,设为:V8,V9,V10。ei( i=1,2,…,10)表示对应变量Vi(i=1,2,…,10)的残差变量。将数据载入的初始模型后,得到图2结果。

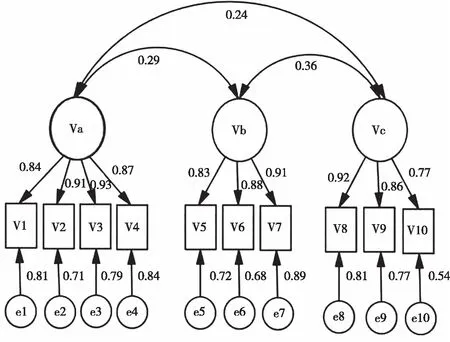
图2 参数估计结果图

(5)模型拟合评价

本研究中,我们选用了能反映验证性因素分析结果的有效性的标准拟合指数NFI、相对拟合指数TLI、比较拟合指数CFI、近似误差均方根指数RMSEA四项指标加以考察。本研究中TLI为0.835,如果TLI0.8,则认为模型拟合较好;CFI为0.916,一般认为CFI0.9模型拟合较好;RESEA为0.046,一般认为RESEA<0.05,表示模型拟合非常好(如表10所示)。

表10 数学文化对学生数学核心素养测评模型的拟合度

模型与数据之间的拟合情况良好。通过验证,采用该模型。

(6)测评模型专家评价

为确保测评模型的科学性,本研究编制了“数学文化对数学素养发展作用的测评模型认同度调查问卷”。问卷采用李克特五级量表记分方式,邀请20名专家(包括高校教育学教授5名、小学数学教研员7名、长期从事数学文化研究、数学核心素养研究的人员8名)对本研究构建的数学文化对学生数学核心素养发展作用的测评模型进行评价。结果显示(如表15所示),专家对各维度能有效反映数学文化对学生数学核心素养发展作用的认同度为86%～100%,对所构建的测评模型的认同度为86%。因此,专家们认为,本研究构建的数学文化对学生数学核心素养发展作用测评模型能对数学文化对学生数学核心素养发展作用进行有效测评。

调查结果表明,该测评模型由三个维度构成,贡献率依次为:情感观念价值维度>关键能力维度>必备品格维度。三个维度与数学文化对数学核心素养发展作用总分显著相关,测评模型拟合指数均符合要求,这一结论具有理论意义。其中,情感观念价值的解释率最高,这可能是因数学的历史发展、数学与生活、数学与艺术等的联系与价值等数学文化的鲜明人文特征与应用价值等,对打破小学生以往对于数学的情感态度、数学观、数学价值的认识,产生了显著影响,即小学生对数学的发展、数学与其他学科的跨学科联系的了解,深刻改变了小学生的数学情感态度和价值观念。而数学与数学家的精神、思想、方法等对发展小学生的数学关键能力和品格塑造也起到了重要的积极影响。

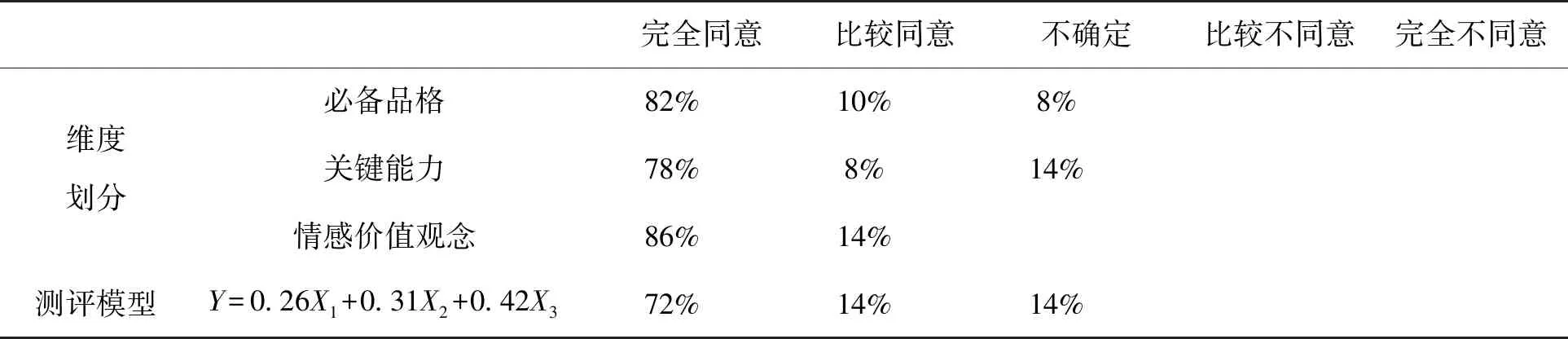
表11 数学文化对学生数学核心素养发展作用测评模型认同度调查情况

通过以上的项目分析,最终确定了《数学文化对学生数学核心素养发展作用测评量表》。再次对C、D两所小学的101名小学生进行测试。最后,通过因素分析中因子得分,以三个因子的方差贡献率占总方差贡献率的比重作为权数进行加权计算,得出三个因子的权数是26.31%(必备品格)、31.28%(关键能力)、42.37%(情感观念价值),分别通过3个一级维度综合反映数学文化对小学生数学核心素养的发展作用。即数学文化对小学生数学核心素养发展作用的测评模型为:

Y=0.26X1+0.31X2+0.42X3

其中,Y为数学文化对小学生数学核心素养发展作用,X1为必备品格维度,X2为关键能力维度,X3为情感观念价值维度。

综上所述,本研究建立的数学文化对学生数学核心素养发展作用测评模型既通过了信效度检验,具有科学性和有效性,也获得了相关专家的认可,可以对数学文化作用下小学生的数学核心素养进行有效测评。

本研究首次构建出数学文化对学生数学核心素养发展作用的指标体系与测评模型,经过初步试验证实该模型可操作并有效,为评价数学文化对学生核心素养发展提供了比较科学的测量工具,比较科学地回答了“数学文化对学生数学核心素养的发展作用”“从哪些维度评价数学文化对学生数学核心素养发展的作用”等问题。为验证该测评模型的外部效度与实用性,本研究还运用该模型对重庆市多所小学的学生进行了更大规模地实地测评、课堂观察等,进一步完善并量化了该测评模型。当然,由于自身能力及时间、地区等主客观条件的限制,我们所建构模型仍需进一步完善。