基于恒应变方法的碳纳米管/聚酰亚胺复合材料的粗粒化力场开发

李华雷,杨 斌,李云龙,,王世杰

(1.汕头大学 工学院土木与环境工程系, 广东 汕头 515063; 2.沈阳工业大学 机械工程学院, 辽宁 沈阳 110870)

1 前 言

自1991年碳纳米管(CNT)被日本科学家发现以来,其优异的电学、力学和热学性能引起了广泛关注[1]。超高的杨氏模量和抗拉强度使其成为高性能聚合物基复合材料的首选增强填料[2-5],在CNT 增强聚合物复合材料的力学性能方面,学者们进行了广泛的实验研究。汪华锋等[6]利用催化裂解制备的CNT/环氧树脂复合材料,力学性能测试表明:CNT 可以使环氧树脂基体材料的拉伸及压缩强度分别提高284%和122%,同时也可增加环氧树脂材料的韧性。蓬勃等[7]制备了质量分数不同的CNT/聚乙烯(PE)复合材料显示:当填充0.5 wt%的CNT 时,断裂伸长率达到最大值429.2%,再进一步增加CNT 填充量,其断裂伸长率呈单调下降趋势。由于受到时间和空间尺度的限制,在纳米尺度下材料间的交互过程和作用机制(如CNT 和基体之间的界面相互作用)等问题的探索在实验中仍然难以有效开展。分子动力学(MD)模拟作为近年来新兴的研究手段,可以在分子层面模拟纳米复合材料基体内的交互过程和作用机制[8-9],成为弥补实验研究局限性的有力补充。Frankland等[10]采用MD方法研究了(10, 10)单壁CNT(SWCNT)增强PE 基复合材料的应力-应变曲线。结果表明,长径比为10的长SWCNT 纤维增强的纳米复合材料的刚度显著增加,对于长径比为4的CNT 增强体,则没有观察到有显著的增强。Li等[11]采用MD模拟方法研究了具有预定单边裂纹的CNT/环氧树脂复合材料的断裂行为。结果表明,引入CNT后,环氧复合材料的拉伸强度和断裂伸长率分别提高了24.8%和34.3%。Mokashi等[12]对(10, 10)CNT 增强非晶态PE聚合物基体的杨氏模量和拉伸强度进行了MD模拟研究,纳米复合材料的模拟单元尺寸设置为4.5 nm×4.5 nm×4.4 nm。模拟结果表明,CNT/聚合物复合材料的纵向杨氏模量为82 GPa,是纯非晶聚乙烯的25倍左右。

虽然MD 已经广泛应用于纳米复合材料领域,但MD 模拟计算的力场复杂,致使工作量巨大,效率较低,使其难以进行更大时间和空间尺度的模拟。为了克服该问题,粗粒化(CG)方法得到了发展[13-15]。CG的原理是将一组原子看作一个整体,忽略内部信息,然后映射成对应的粗粒化珠子,从而保持原子模型的分子细节的同时,成倍缩减全原子体系的自由度和粒子数,增大模拟的时间和空间尺度。目前,已有文献进行了聚合物材料的粗粒化模型及其力场参数的初步开发工作[16-18]。Marrink 课题组用粗粒化方法得到了MARTINI力场[19],主要用于研究生物大分子的动态行为,比如磷脂分子、蛋白质及DNA 等。蔡庄立等[20]根据特定的映射方案建立了PE 的粗粒化模型,并以全原子模型的键长、键角分布曲线来获取PE 的粗粒化力场参数。文中验证了粗粒化参数模拟PE 模型的静态结构分布,且粗粒化模型的导热系数的模拟值与实验值符合较好。Langeloth等[21]利用玻尔兹曼反转迭代法得到了环氧树脂的粗粒化模型以及力场参数,并利用此参数在更大的尺度下研究了环氧树脂的玻璃化转变温度与交联程度的变化关系。

然而由于目前的粗粒化研究缺少对粗粒化力场参数准确性的验证,粗粒化力场参数与模型物理性能之间的关系亦鲜有讨论。同时,已有的玻尔兹曼反转迭代法[22-23]等方法操作复杂,适用范围有限。本研究使用基于应变能守恒定律的恒应变方法获得聚酰亚胺(PI)和CNT 的力场参数,然后通过不同模拟实验来验证粗粒化参数的准确性,最后对粗粒化参数与物理性能的关系将进行详细讨论。

2 建模与粗粒化参数的获取

粗粒化力场参数主要由成键势函数和非键势函数两部分构成。体系总势能Etotal可以写成键长能Eb、键角能Ea、范德华能Evdw和系统恒定自由能U0之和,表达式形式如下:

式中组成总势能的各个势函数函数形式如下:

式中:kd和d0是键长的刚度系数和平衡键长;kθ和θ0是键角的刚度系数和平衡键角;D0和r0分别是Lennard—Jones(LJ)势函数的势阱参数和平衡距离。全原子模拟使用COMPASS力场来描述分子内的相互作用力,非键相互作用的截断半径取1.2 nm,能量最小化方法使用共轭梯度法。

2.1 粗粒化键长参数的获取

粗粒化第一步是根据设计好的映射方案将原子团映射成粗粒化珠子。如图1所示,组成PI的每个单体被映射为两个粗粒化珠子A(C8H3NO2)和一个粗粒化珠子B(C6H4),将(5, 5)的CNT 中每50个碳原子映射成1个粗粒化珠子C(C50),以原子团的质量中心为粗粒化珠子的中心。A 珠子的相对原子质量为145.21,半径为2.61 Å;B 珠子的相对原子质量为70.09,半径为1.94 Å;C 珠子的相对原子质量为600.55,半径为3.96 Å。

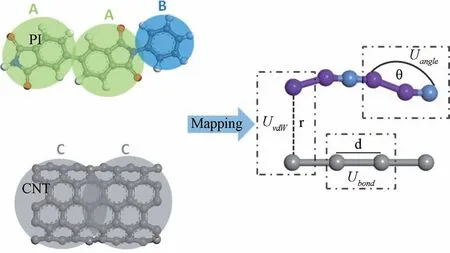
图1 PI和CNT 的粗粒化映射方案Fig.1 Coarse-grained mapping scheme of polyimide (PI)and carbon nanotube (CNT)

接下来使用恒应变方法获取粗粒化力场参数。首先改变A-A 珠子对应的原子团之间的键长,通过分子模拟得到体系的总势能U,根据应变能守恒,粗粒化体系的总势能也等于U:

得到d0=6.78 Å,图2(a)展示了U与Δd的变化曲线。kd由式(6)求出:

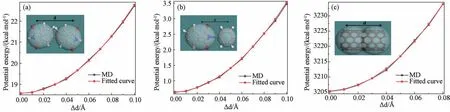
图2 原子团势能与键长增量的变化 (a)A-A 原子团;(b)A-B原子团;(c)C-C原子团Fig.2 Variation of potential energy versus deformation of bond between (a) A-A group; (b) A-B group; (c) C-C group

得出kd=400.56 kcal·mol-1·Å-2。

同样地,改变A-B珠子对应的原子团之间的键长,得出U与Δd的变化曲线。如图2(b)所示,根据式(5)、(6),依次得到d0=4.80 Å,kd=340.78 kcal·mol-1·Å-2。改变C-C 珠子对应的原子团之间的键长,得出U与Δd的变化曲线,如图2(c)所示。根据式(5)、(6)得出:d0=6.12 Å,kd=4 542.0 kcal·mol-1·Å-2。

2.2 粗粒化键角参数的获取

改变A-A-B珠子对应的原子团的角度,通过分子模拟得到体系的总势能U,根据应变能守恒,粗粒化体系的总势能也等于U:

得到θ0=158.8°,整理出U与Δθ的变化曲线,如图3(a)所示。kθ由式(8)求出:

图3 原子团势能与键角增量的变化 (a)A-A-B原子团;(b)A-B-A 原子团;(c)C-C-C原子团Fig.3 Variation of potential energy versus the bond angle’s deformation of (a) A-A-B group; (b) A-B-A group; (c) C-C-C group

得出kθ=980.80 kcal·mol-1·rad-2。

同样地,改变A-B-A 珠子对应的原子团的角度,得到U与Δθ的变化曲线,如图3(b)所示。根据式(7)、(8)得出θ0=179.4°,kθ=670.21 kcal·mol-1·rad-2。最后,改变C-C-C珠子对应的原子团的角度,得出U与Δθ的变化曲线,如图3(c)所示。根据式(7)、(8)得出θ0=180.0°,kθ=66 880.0 kcal·mol-1·rad-2。

2.3 粗粒化范德华参数的获取

改变A-A 珠子对应的原子团间的距离r,得到内聚能U随r的变化曲线,如图4所示。U是体系范德华能与单个原子团的范德华能之间的差值。U的最小值作为D0,U的最低点对应的横坐标为r0,得出A 珠子的D0=7.56 kcal·mol-1,r0=4.01 Å。以同样地步骤获取其余珠子的D0和r0,整理成表1。

表1 A、B、C珠子的势阱参数D0 与平衡距离r0Table 1 Well depth (D0) and equilibrium distance(r0) of beads A, B and C

图4 A-A 原子团的势能与距离的变化Fig.4 Variation of energy versus distance between A-A group

利用得到的粗粒化参数对CNT/PI复合材料的粗粒化模型进行充分弛豫,然后将弛豫后的粗粒化模型的结构分布曲线,包括键长、键角以及径向分布曲线,与全原子模型的进行对比,并根据分布曲线的误差修正粗粒化力场参数,最后得出调整后的参数,如表2所示。

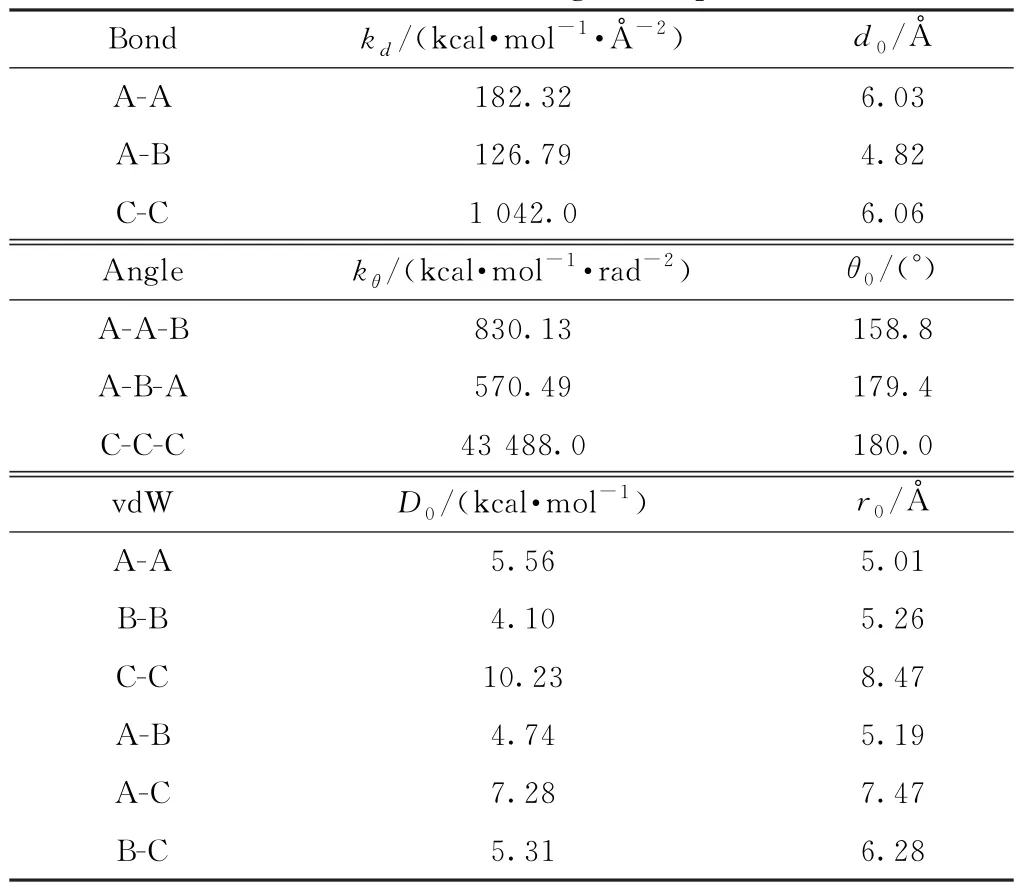
表2 修正后的粗粒化参数Table 2 Modified coarse-grained parameters

表3 PI链与CNT的杨氏模量Table 3 Young's modulus of PI chain and CNT

3 粗粒化参数的验证和探讨

3.1 验证PI分子链和CNT的拉伸性质

如图5(a)所示,一条PI分子链含有四个单体,一条PI珠子链含有8个A 珠子,4个B珠子,分子链的长度为66.17 Å,对两条链进行拉伸,应变率为8%,得到图6(a)中的应力-应变曲线。对曲线进行拟合得到全原子与粗粒化PI链的杨氏模量分别为16.82 和17.18 GPa,相对误差为2.1%。图5(b)展示的是(5,5)的CNT(C500)和含有10个C 珠子的CNT 的周期性模型,从图6(b)的应力-应变曲线得出全原子与粗粒化CNT 的杨氏模量分别为183.0和178.0 GPa,相对误差为2.7%。两组曲线表明粗粒化力场参数能准确还原PI与CNT 的拉伸性能。

图5 全原子及粗粒化模型 (a)PI链;(b)CNTFig.5 All-atomic and coarse-grained model of (a) PI; (b) CNT

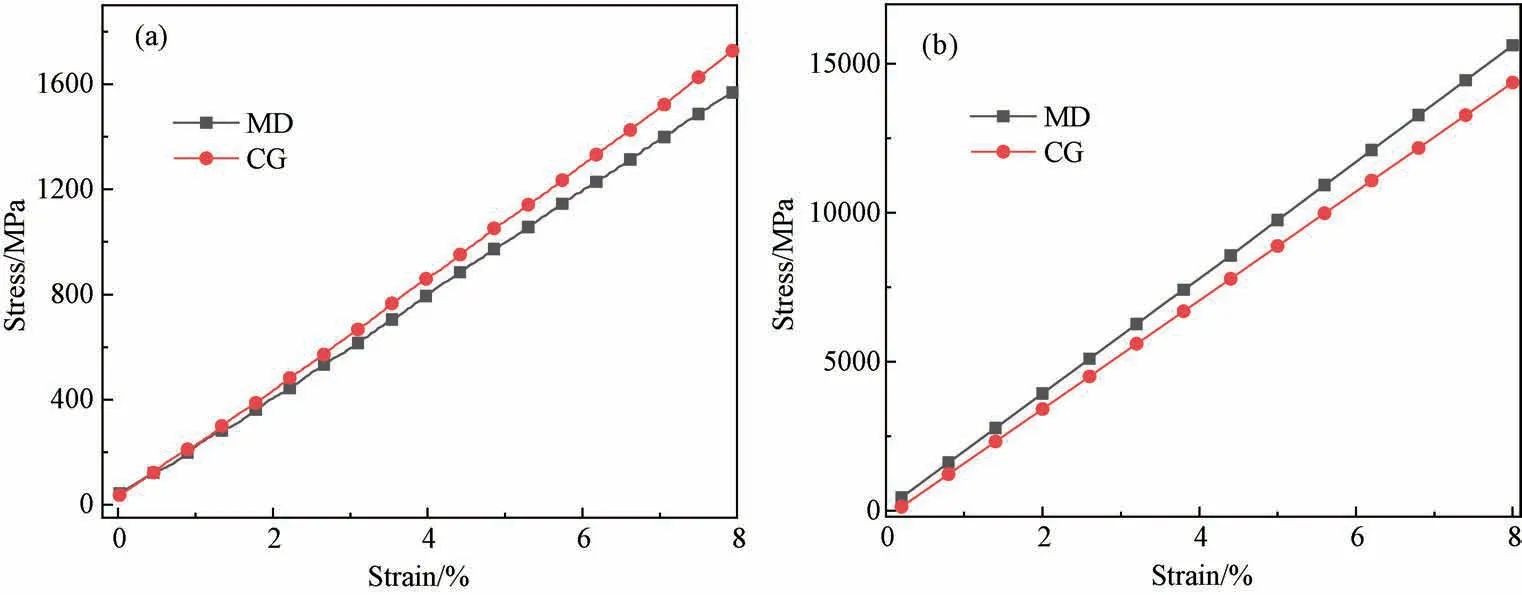
图6 全原子与粗粒化的应力应变曲线(a)PI;(b)CNTFig.6 Stress-strain curves between all-atomic and coarse-grained model of (a)PI chain; (b)CNT

3.2 验证CNT/PI复合材料的物理性质

利用Accelrys Materials Studio 8.0 软件的Amorphous Cell Packing模块将含有4 个单体的PI分子链填充到盒子中,并将一根(5, 5)的CNT 置于盒子中间,建造一个大小为6.0 nm×6.0 nm×6.0 nm的CNT/PI复合材料的周期性模型,全原子模型共包含16 650个原子。通过全原子模型映射而成的粗粒化模型包含2 580个粗粒化珠子,模型的自由度相对于全原子的减少了约8倍。

首先对模型进行充分的结构几何优化,然后在NPT 系综下对模型进行动力学弛豫,弛豫温度设为298 K,压强为101 kPa,全原子和粗粒化模型的时间步长分别设置为1 fs和10 fs,弛豫总时长为1.5 ns。全原子模型弛豫耗时约18 h,粗粒化模型耗时约1.5 h,粗粒化后模拟效率可提升约10倍。图7展示了全原子和粗粒化模型的密度随时间的变化曲线,平衡密度分别为1.185和1.184 g/cm3,相对误差为0.8%。模拟结果表明粗粒化力场参数可以准确模拟出纳米复合材料的密度。

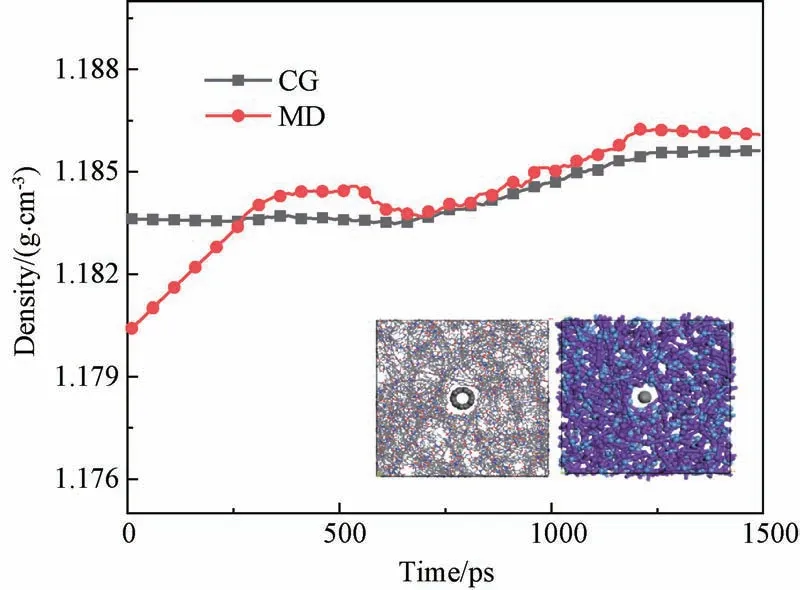
图7 CNT/PI复合材料的密度变化Fig.7 Variation of the density of CNT/PI composites

接着利用经过充分弛豫的全原子和粗粒化模型进行CNT 的拔出模拟,以此验证CNT 与PI基体间的界面相互作用。如图8(a)展示了CNT 的拔出模型,将CNT 沿着z轴方向以0.000 1 Å/fs的恒定速度拔出,输出拔出能,并绘制出拔出能随拔出距离变化的曲线,如图8(b)所示。CNT 的拔出模拟是通过在CNT端部系一根弹簧,让弹簧以固定速度移动,实现CNT的拔出,拔出力等于弹簧的拉力,拔出能等于拔出力与CNT 位移的乘积。

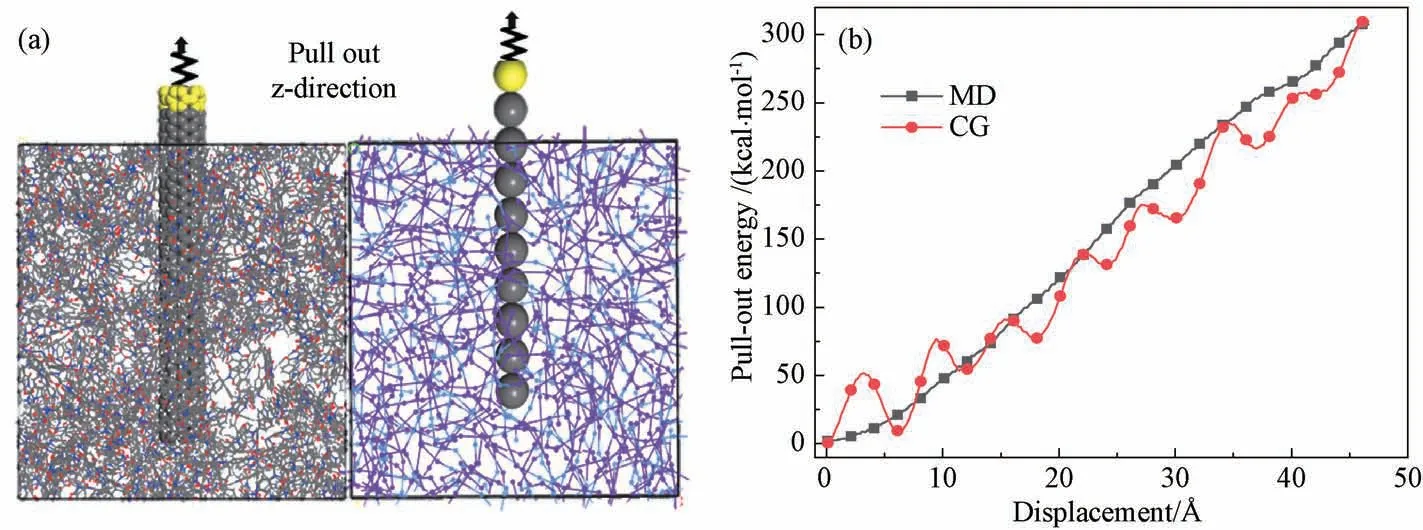
图8 全原子与粗粒化CNT/PI复合材料的(a)CNT 拔出模型;(b)CNT 拔出能与拔出位移的曲线Fig.8 (a) Schematic illustration of CNT pull-out process; (b) pull-out energy response versus pull-out distance

图8中粗粒化模型的拔出能呈现周期波动的原因是 CNT的粗粒化模型中的 C 珠子之间相距较远,所以不能被近似看成连续一维材料,导致拔出能在 C珠子离开基体过程中具有明显的周期性变化。从图8(b)中可以看出,粗粒化模型的拔出能曲线保持在全原子模型的拔出能曲线上下波动,该模拟结果证明粗粒化力场参数可以还原出CNT和PI基体的界面相互作用。

最后将纳米复合物沿着z轴方向拉伸,应变率为2%,全原子和粗粒化模型的应力-应变曲线如图9b所示。全原子与粗粒化模型的杨氏模量分别为8.13和8.16 GPa,相对误差为3.6%,证明粗粒化力场参数可以准确还原出纳米复合材料的杨氏模量。

图9 全原子与粗粒化CNT/PI复合材料的(a)拉伸模型;(b)应力应变曲线Fig.9 CNT/PI composites between all-atomic and coarse-grained (a) the schematic illustration of stretching process; (b) stress-strain curves

3.3 粗粒化参数对复合材料物理性能的影响探讨

探讨粗粒化参数对模型的影响有助于深入理解粗粒化各项参数对模型的物理性质的影响效果和影响程度,便于后续对参数的修正,使粗粒化模拟更加准确、适用性更强。该部分主要探讨范德华参数中的r0和D0对CNT/PI复合材料的物理性能的影响,内容包括密度、CNT 与PI基体的相互作用以及小应变下的拉伸性能。小应变下,影响拉伸性能的主要的分子间的相互作用力,键长键角的参数主要与大应变下的拉伸性能有关。

3.3.1r0对密度的影响 式(4)表明,D0与分子间相互作用有关,r0与分子间的距离有关。增加A、B和C珠子的r0,Δr0依次取值0、0.3、0.6和1.0 Å,然后在NPT 系综下对模型动力学弛豫,绘制不同力场参数下模型的密度随时间变化的曲线,如图10所示。随着Δr0从0增加到1.0 Å,模型的平衡密度从1.18减小到0.84 g/cm3,结果表明:r0增加,模型密度减小。

Δr0/Å Density/(g·cm-3)0.0 1.18 0.3 1.07 0.6 0.95 1.0 0.84

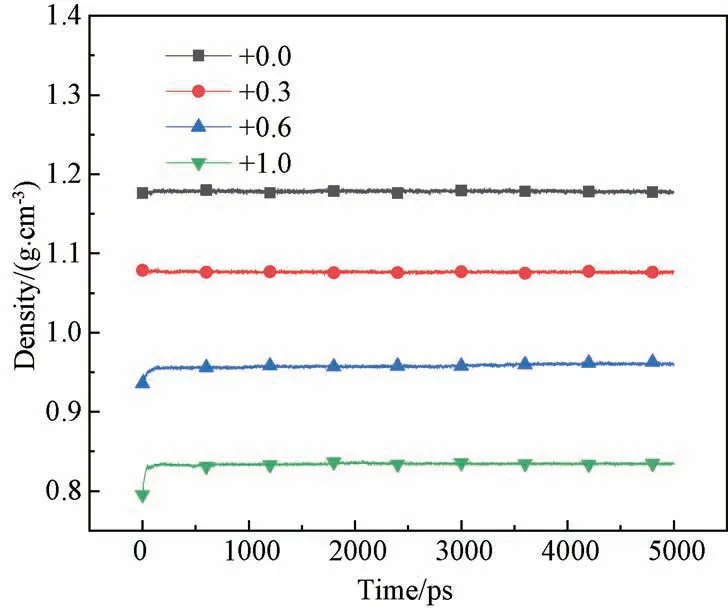
图10 不同r0 下模型密度随时间的变化Fig.10 Variation of density versus r0

3.3.2D0对界面相互作用的影响 在CNT 的拔出模拟中,拔出力要克服CNT 与PI基体间的相互作用力做功。可以通过不同D0下CNT的拔出能与拔出距离的变化曲线,比较界面相互作用强度。将C珠子与A、B珠子间的D0分别增加0、2、4和8 kcal·mol-1,然后进行CNT的拔出模拟,并绘制不同D0下CNT的拔出能随位移变化的曲线。如图11所示,结果表明:CNT与PI间的D0越大,界面相互作用越大。

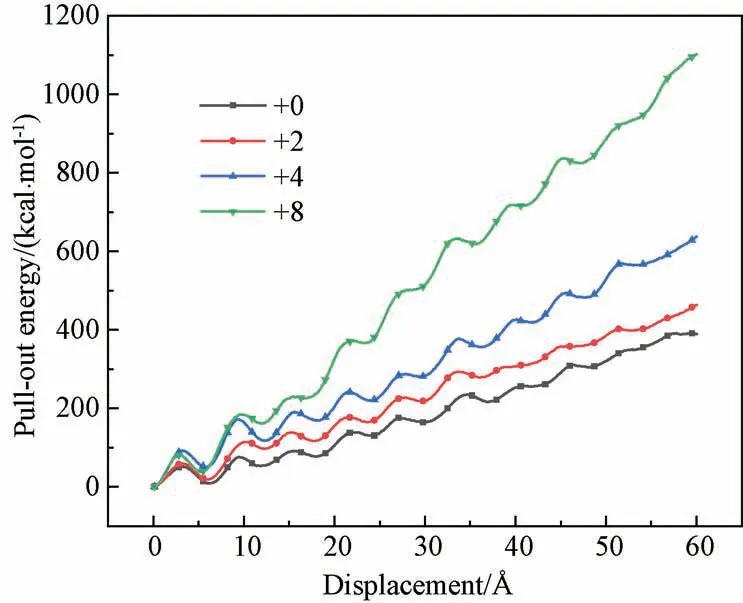
图11 不同D0 下CNT 拔出能随位移变化的曲线Fig.11 Curves of CNT pull-out energy versus displacement with different well depth parameters

3.3.3D0对杨氏模量的影响 探究D0与CNT/PI复合材料的杨氏模量的关系。改变D0,ΔD0分别取0.0、2.0、4.0及6.0 kcal·mol-1,模型进行拉伸模拟,应变率为3%,整理出不D0下模型的应力应变曲线,如图12所示。由图12和表5可以得出结论:在弹性拉伸阶段,D0越大,分子间相互作用力越大,纳米复合材料的杨氏模量越大。

表5 不同势阱参数与对应的复合物的杨氏模量Table 5 Different well depth parameters and corresponding Young's modulus of nanocomposite

图12 不同势阱参数下模型的应力-应变曲线Fig.12 Stress-strain curves of the model with different well depth parameters

4 结 论

1.根据相应的映射方案,利用恒应变方法可以完整地得出PI与CNT 的粗粒化力场参数。

2.PI分子链以及CNT 的拉伸模拟中,粗粒化模型与全原子模型的杨氏模量的相对误差低于5%,证明粗粒化力场参数能准确还原单链的拉伸性质。

3.粗粒化模型可以成倍减少原子数,并使得模拟效率提高约10倍。

4.在CNT 拔出模拟中,全原子与粗粒化模型的CNT 拔出能与拔出距离的变化曲线基本吻合,证明粗粒化力场参数可以准确还原CNT 与PI基体间的界面相互作用。

5.对模型进行拉伸模拟,得出全原子与粗粒化模型的杨氏模量的相对误差低于5%,证明粗粒化力场参数可以还原复合物的弹性拉伸性质。

6.在关于粗粒化力场参数与材料物理性能的关系的研究中得出结论:分子间的平衡距离r0增加,模型体积增大,密度减小;势阱参数D0增加,分子间作用力增加,CNT 与PI基体的界面相互作用增大,杨氏模量增加。该结论可为未来利用粗粒化方法探索CNT表面缺陷、不同改性等因素对复合基体性能影响方面提供理论支撑。