主成分分析法在园林专业学生成绩评价中的应用

崔 珺，潘 健

（黄山学院生命与环境科学学院，安徽 黄山 245041）

0 引 言

学生成绩评价是高校教学管理的重要组成部分[1]，对学生的成绩进行分析有利于教师了解学生对课程的掌握情况，而成绩评价体系对学生在校期间的奖惩、后期的深造和就业都有很大影响。早期的成绩评价主要采用平均成绩和学分绩点评价等方式进行[2]，随着信息技术不断革新，众多学者将多元分析引入学生成绩评价体系中[3，4]，主要以因子分析[5，6]、主成分分析[7]和聚类分析[8，9]为主，亦有综合两种方式进行分析的案例[10，11]。采用统计的方法来进行成绩评价可以将复杂的指标简单化，解决定量或定性分析中存在的问题[12]，便于进行成绩评价。基于以上原因，结合园林专业课程特点和主成分分析法进行学生成绩评价，以期为后期学生成绩评价提供参考依据。

1 研究对象和研究方法

1.1 研究对象

以黄山学院生命与环境科学学院园林专业2018届、2019届和2020届3届毕业生的基础课和专业课课程成绩为例，运用主成分分析法对学生的综合学习效果和综合能力进行评价。三届学生人数不一致，每届随机抽取90 名共270 名学生的课程成绩作为研究对象。园林专业开设课程较多，如表1 所示，经过对培养方案的梳理研讨初步遴选了20门课程作为变量。选择的课程包括10门基础课程A1-A10；10门专业课程B1-B10，以上20门课程对应的成绩分别用x1，x2，…，x20来表示，这样即可得到一个270×20的数据矩阵，使用SPSS 22.0进行主成分分析。

表1 用于分析的课程及编号

1.2 研究方法

主成分分析法的基本思想为对问题的原始指标做线性组合形成综合指标，按方差大小进行排序，选取前几个综合指标，依次定义为第一、第二、第三主成分等。这些主成分间是线性无关的。这样处理，既能降低问题的复杂度，又能从原始数据中进一步挖掘实际问题的某些新信息[13，14]。

在实际问题中，为了降低分析的难度，提高分析效率，通常不直接对原始指标（p个）构成的随机向量x=（x1，x2，…，xp）进行分析，而是先对向量做线性变换，把原来的随机向量变换成新的综合变量y1，y2，…，yp。变量y1，y2，…，yp之间相互独立，并且其方差依次递减。下面用两个向量对问题进行说明，考虑通过线性变换，将x1和x2进行线性组合，得到两个新的变量y1和y2。从几何角度来看，就是将坐标系逆时针旋转θ角度，得到新坐标轴y1和y2，具体坐标旋转公式如下[15]：

式中，U为旋转变换矩阵，由（1）可知它是正交阵，即满足式（2）：

从相关系数矩阵开始，求解主成分的步骤：

1.标准化各观测变量数据；

2.求各观测变量标准化后的相关系数矩阵；

3.根据矩阵知识|ρ-λI|=0，求解相关系数矩阵的特征根；

4.求解各特征根对应的特征向量ρμi=λiμi。

其中，第一主成分的系数向量为最大特征值对应的特征向量；第二主成分的系数向量为第二大特征值对应的特征向量，同理可以得到其他系数。

2 结果与分析

2.1 相关系数矩阵

将270名学生的课程成绩作为原始数据进行处理，首先将原始数据进行标准化并计算相关矩阵得到表2。由表2 可以看出，在被进行统计的20 门课程中，有5 门基础课程，包括气象学、绘画1、绘画2、园林设计初步和园林史,与10 门专业课程成绩间呈极显著正相关，1 门基础课程植物学与除园林规划设计1 以外的9 门专业课程成绩间呈极显著正相关，除少数课程间呈现负相关外，多数课程之间的相关系数都达到了显著正相关或极显著正相关，这表示大多数课程成绩具有较强的关联性，即某门课程的成绩的波动，可由另外一门课程成绩分布规律来进行推断。

表2 课程成绩(变量)间相关系数

以花卉学和园林树木栽培学为例，二者之间的相关系数最高，达到0.669，这表明花卉学掌握较好的同学，其园林植物栽培学掌握的也较好。此外，对于园林专业开设的基础课程和专业课程进行相关性分析时，可以看出对气象学、绘画1、绘画2、园林设计初步和园林史这5门基础课程与园林专业开设的专业课程相关性均呈正显著相关，这充分说明园林专业基础课程的设置对于园林专业学生学习专业课具有重要的影响。园林规划设计2、园林建筑、园林植物造景、花卉学1和园林树木栽培学与所有的专业基础课均呈现显著相关，这5 门课程也是生物类专业重要的专业课程，这有力地验证了学好基础课程对专业知识的掌握至关重要。

2.2 公因子方差分析

由输出结果公因子方差看出，表3 中最后一列的数据均在50%以上，表明提取的主成分对每个变量的解释程度都较高。

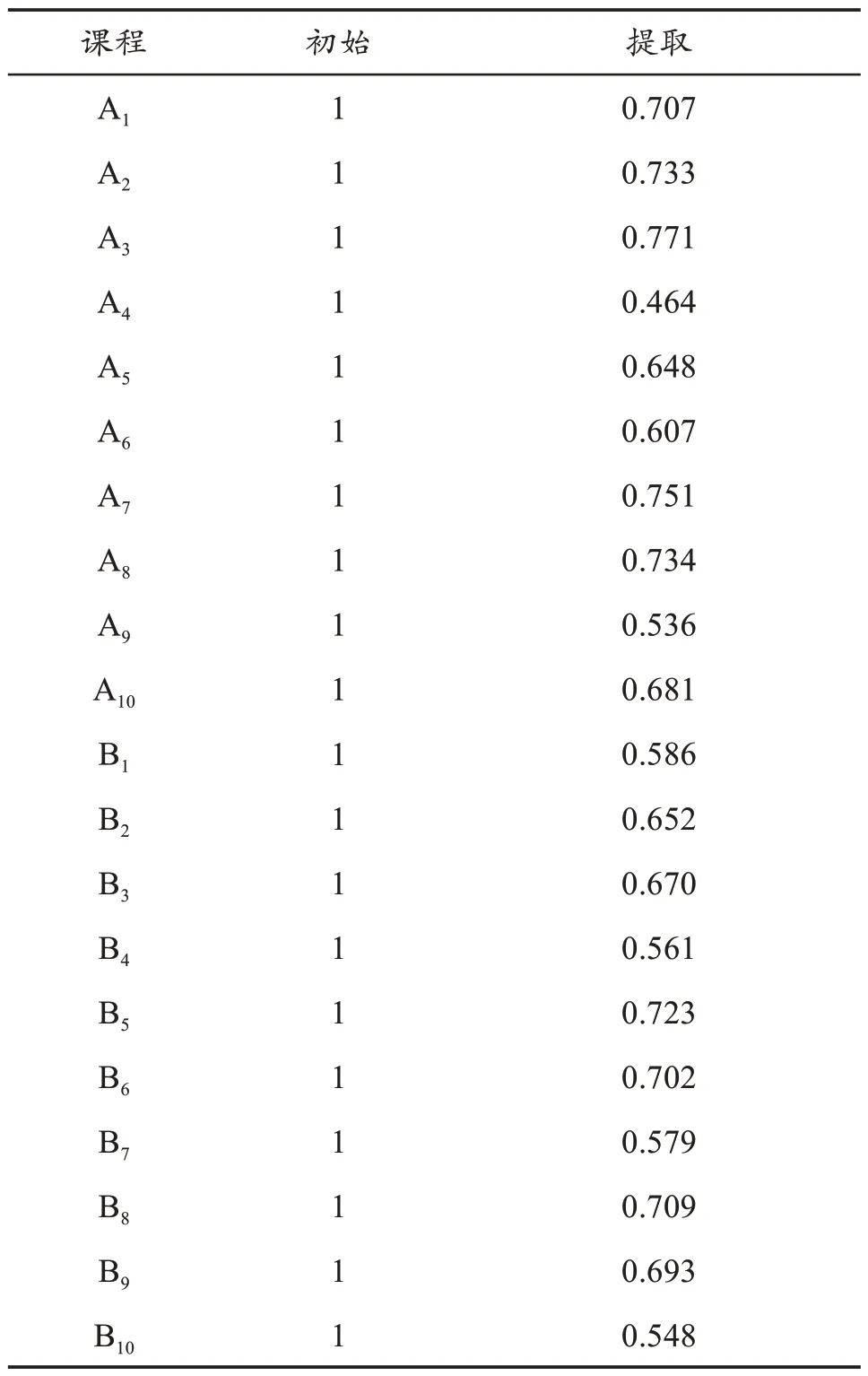
表3 公因子方差分析

2.3 解释的总方差

如表4 所示，由输出结果图的总方差可以看出前4 个主成分y1，y2，y3，y4的方差之和占总方差的比例达到了65.281%。所以，前4 个主成分就可以基本保留了原来指标的信息，这样就由原来的12个减少为4 个新指标，从而起到了降维的作用。第一主成分的方差贡献率为38.399%，即第一主成分可以反映原指标38.399%的信息量，表示第一主成分承载了学生成绩的主要综合信息。前4个主成分的累计方差贡献率达到65.281%，若按照60%的判断标准，只需选取前4 个主成分就可以代表原来20 个指标所包含信息量的65.281%。

表4 主成分的特征值、方差贡献率和累计贡献率

表5 给出了4 个主成分的特征向量和相应的载荷值。第一主成分对应的特征向量和载荷值均为正值，数值上也相差较小，即第一主成分可以反映学生的综合学习成绩。第一主成分在园林植物造景、园林树木学2、花卉学1 和园林树木学栽培学这4门专业课程上的载荷值较大，通过分析可知这4门课程在第一主成分中起作用较大，因此在专业学习中这几门课程学的怎样就直接影响学生的综合专业素质。第二、三、四主成分的方差贡献率分别是12.084%、9.442%和5.356%，且在各门课程上的荷载值存在负值，在学生综合成绩评价上容易产生偏差，因此直接采用第一主成分对学生综合成绩进行评价更合理。

表5 4个主成分的特征向量和相应的载荷值

由表5中成分得分系数矩阵可以得到主成分表达式。

第一主成分：

以此类推，还可以写出其余3 个主成分的得分表达式。

第二主成分：

第三主成分：

第四主成分：

对于学习综合成绩的优劣也可以通过综合评价得分体现，以4个主成分所对应的特征值（见表4）占所提取主成分总的特征值之和的比例作为权重，计算主成分综合模型，根据主成分综合模型即可算出综合主成分值。其表达式为：

其中λ1=7.680；λ2=2.417；λ3=1.888；λ4=1.071；

本研究中最终可以得到表达式为：

将学生的成绩标准化后的数据代入Y1、Y2、Y3、Y4和Y的表达式中，就可以得到每个学生的主成分得分和综合得分，再对随机抽取的20名学生的课程成绩进行综合排名。从表6 中可以看出，第一主成分得分给出的排名与4个主成分的综合成绩得分提供的排名十分接近，平均分与主成分排名差距较小。从表5 中每个学生的综合成绩得分、总成绩平均分以及4 个主成分方面的得分情况，可以进一步判断学生在综合素质和学科上的优劣。

表6 综合排名（部分）

3 结 论

学生成绩可以反映学生对课程的掌握情况以及教学中需要教师注意的部分，但是单纯通过20门课程来评价学生课程掌握情况又是一个复杂的问题。研究采用主成分分析的思想与实际教学情况相结合，从枯燥的各科目成绩中挖掘出很多信息，如各门课程成绩之间具有较强的相关性，学好基础课程对后期专业课程学习有很大的影响；园林植物造景、园林树木学2、花卉学1、和园林树木栽培学这几门课程的掌握很大程度上影响学生对专业课程的学习以及综合素质的提高等。研究只是选择基础课和专业课进行统计分析，没有考虑公共课和选修课对学生学习成绩的影响，可能在分析综合成绩方面存在偏差。但是通过以上的数据分析，还是能发现教学的一些规律，旨在为园林专业教育教学改革提供科学的方法和理论依据。