2A12/6061异种铝合金搅拌摩擦连接工艺参数优化

黄 达，汪洪峰,，王建彬，宋娓娓，姜 迪

（1.安徽工程大学机械工程学院，安徽 芜湖 24100；2.黄山学院机电工程学院，安徽 黄山 245041）

铝合金有着低密度、高耐腐蚀性以及较好的导电导热性能，使其广泛应用于航空、汽车、船舶、高铁等机械制造领域。铝合金有着多种类型，不同系列铝合金，其性能和应用范围都差异较大。在某些特定领域及复杂环境下，单一种类铝合金无法满足设计及生产的需求，因此异种铝合金之间的连接逐渐引发关注。搅拌摩擦连接技术（Friction stir joining，简称FSJ）是一种固相连接技术，通过高速旋转的搅拌头插入到连接两块板材的中间，并通过搅拌头轴肩的挤压以及搅拌头的前进在连接区实现半熔化状态（温度仅为材料熔点2/3）下连接。现阶段从事异种铝合金搅拌摩擦连接研究的人员越来越多。Kumar 等通过对AA6061 和A6082 搅拌摩擦连接的温度变化和力学性能相结合进行优化分析，其结果表明连接接头的抗拉强度随刀具转速的增加而增加[1]。张翅超基于响应面法对钛铝异种金属搅拌摩擦点焊工艺参数优化，建立了焊接工艺参数与拉剪断裂载荷的二阶响应模型，研究了工艺参数对接头拉剪断裂载荷的影响，并通过工艺参数优化预测了点焊接头的拉剪断裂载荷，所建立的模型较为准确，预测值与实验值的平均误差约为2.41%[2]。Shunmugasundaram 等采用正交试验方案，开展AA6063和AA5052异种铝合金之间连接并对工艺参数进行优化[3]。结果表明在搅拌头转速为850r/min，焊接速度为20mm/min，搅拌头倾斜角度为2°时，焊接接头抗拉强度最大。高崇等对比了不同焊接速度条件（100～400mm/min）下3mm厚的5754铝合金板材FSW 接头的性能，随着焊接速度增加，拉伸强度和断后伸长率先增加而后降低，当焊接速度为300mm/min 时，搅拌针区面积达到最大值，强度系数达到最大值的97.5%[4]。Nansaarng 等对1100/6063 异种铝合金进行试验，发现不同搅拌头前进速度会导致连接区显微硬度不同[5]。Hema 等在6061/2014 异种铝合金的连接试验中发现，抗拉强度、显微硬度受前进速度的影响大于搅拌头速度[6]。Guo等发现在合适的范围内过高或过低的下压量，会导致宏观缺陷的产生，如沟槽、隧道或孔洞等缺陷[7]。Muhayat等发现较高的下压量可以消除部分宏观缺陷，并在一定程度上提高搅拌摩擦热输入，消除连接缺陷[8]。基于上述依据，拟开展对10mm 厚的2A12/6061异种铝合金板进行FSJ实验，分析在不同FSJ 工艺参数对连接区力学性能的影响规律，为实际工程应用提供技术支持。

1 试验材料及方法

1.1 试验材料及试验设备

选择50×100×10mm 的2A12/6061 异种铝合金冷轧板作为搅拌摩擦连接的实验材料，其化学成分及力学性能如表1、表2所示。

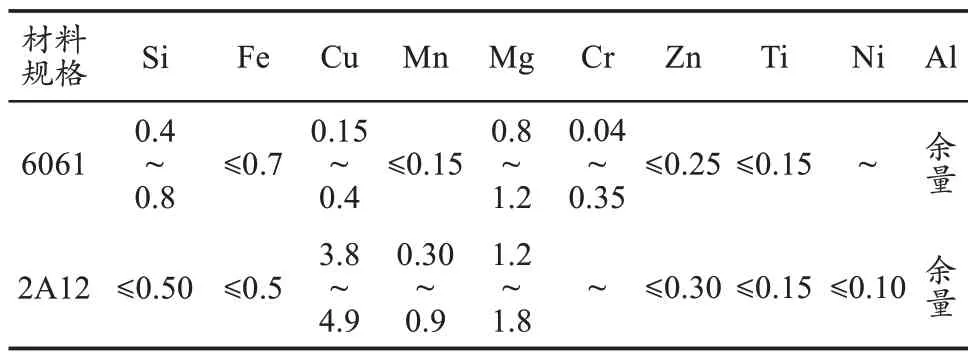
表1 6061和2A12化学成分表（质量分数/%）

表2 6061-T6和2A12-T4力学性能

试验所采用的搅拌摩擦连接设备型号为赛福斯特公司生产的FSW-LM-A10 型搅拌摩擦连接机床。所采用搅拌头轴肩直径为24mm，搅拌针长度为9.6mm，搅拌针为锥形螺纹搅拌针。在进行搅拌摩擦连接之前采用砂纸将待连接区域打磨去除氧化层，之后使用无水乙醇对表面进行擦洗，待其晾干后放置于工作台进行装夹准备。

1.2 试验方案

试验选取搅拌头旋转速度（rpm）、连接速度（mm/min）、下压量（mm）作为线响应面试验的3 个因素，以连接区抗拉强度作为响应值，采用CCD 方法进行试验设计，得到3因素5水平共20个试验点，具体试验方案如表3 所示。试验过程中，6061 始终保持在后退侧，2A12始终保持在前进侧。

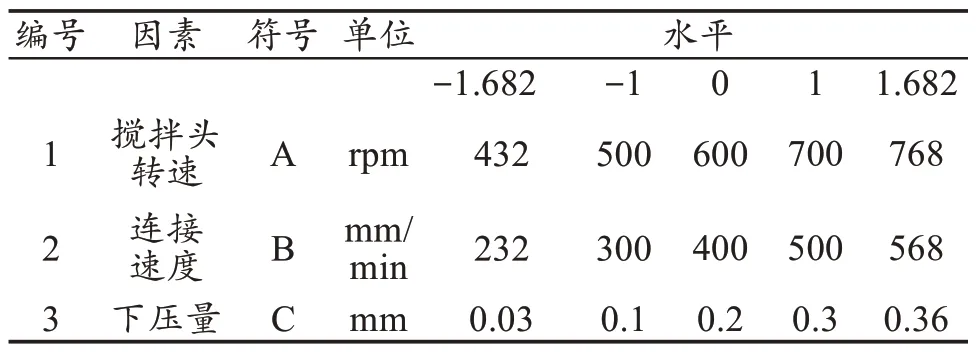
表3 设计参数的实际和编码水平

2 响应面试验结果与分析

2.1 试验结果

在搅拌摩擦连接机床上进行试验，板材连接好后利用线切割机在连接区域切割相应的试样，使用砂纸对试样表面进行打磨去除连接痕迹后，在WAW-1000 万能试验机上进行拉伸实验，拉伸参数及结果如表4所示。

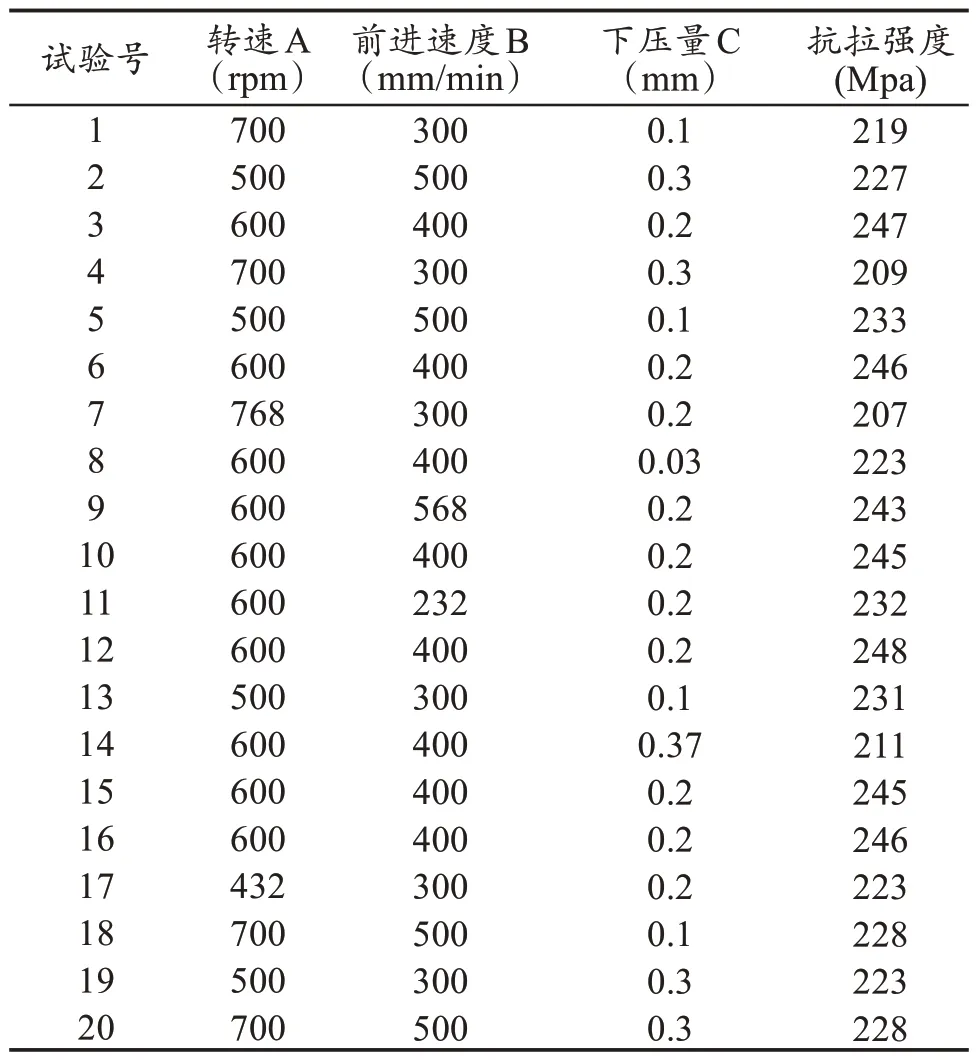
表4 响应面试验设计与结果

采用Minitab Statistical Software 统计并进行f值和p值检测确定各项系数在95%置信水平是否具有显著性影响，并通过方差分析（ANOVA）方法进行回归模型及其系数的显著性检验，以及失拟程度检测，根据表4测试的试验数据进行计算，推导出二阶项式回归模型的系数，二次方差模型回归分析结果如表5所示。

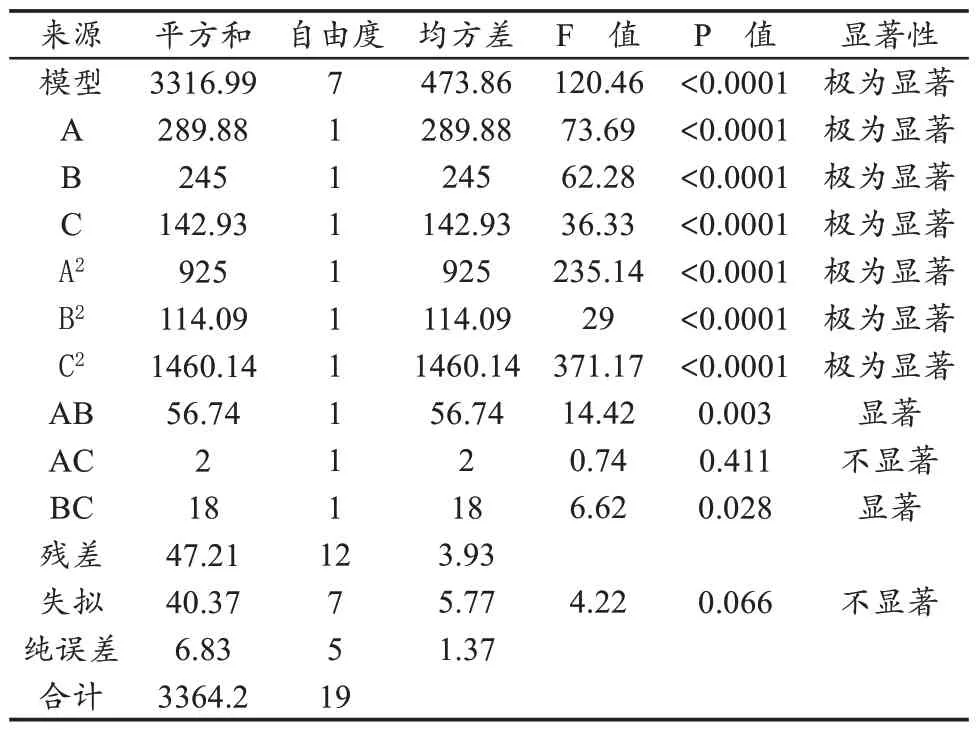
表5 二次方差模型回归分析

响应面优化数学模型主要由参数主效应和交互效应的二阶多项式回归模型组成，建立FSJ 工艺参数与接头抗拉强度之间的数学关系。响应函数为工具旋转速度（A）、焊接速度（B）和下压量（C）的函数，可以表示为：

应用二阶多项式回归方程表示k个因子的响应面Y为：

其中，Y为响应面，er为观测到的误差，bo为响应的平均值，bi、bii和bij分别为一次项、二次项和交互项系数，这些系数采用以下公式进行计算。

采用3 个连接工艺参数建立的多项式可以表示为：

使用Minitab Statistical Software 软件绘制等高线图及三维立体图形，固定单一工艺参数情况下对另外两个工艺参数之间的相互作用进行分析，并排出响应值较低的双因子交互相项，通过和交互项之间的响应关系建立数学模型，并验证数学模型的拟合程度，基于编码因子计算出连接区抗拉强度的数学模型，具体如公式（8）。

2.2 数学模型与精度检验

2.2.1 试验数据残差的正态分布与独立性

使用正态概率分布图校验与模型相关残差的正态性，如图1 所示为抗拉强度的残差正态概率分布图，实验数据残差均分布于直线附近，表面残差符合正态分布法相关特性，试验结果满足正态性假设。

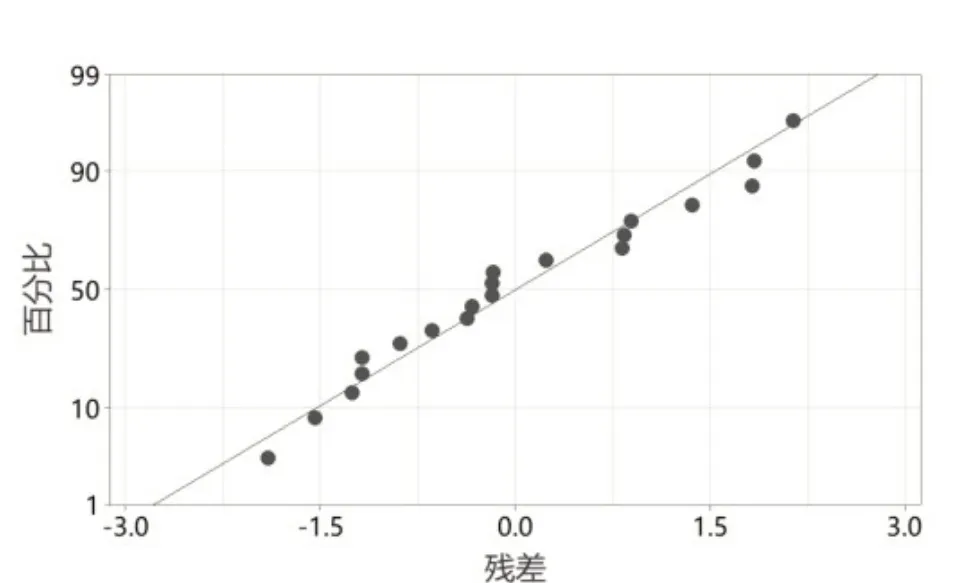
图1 残差的正态概率分布图

为验证所建数学模型的正确性，每组连接工艺参数连接后的接头测试3 次，确定每组抗拉强度的平均值作为实际值。预测值与试验值的关系如图2所示，所有数据点均在拟合值周边分布于，因此预测值与试验值较为接近。

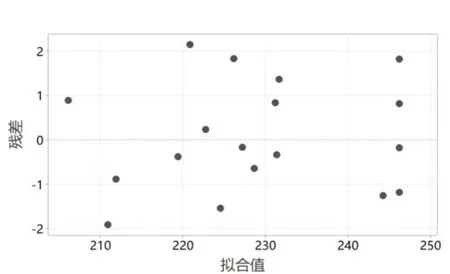
图2 预测值和实际值分布图

2.2.2 连接工艺参数对抗拉强度的影响

在连接过程中，主要热源来源于搅拌头轴肩与待焊板材之间摩擦，且下压量增大会影响轴向力大小的改变，因此下压量增加会产生更多的摩擦热。搅拌头旋转不仅会影响摩擦热量的产生还承担破碎并混合待连接区域的作用，连接速度影响连接过程中单位距离内搅拌头工作时间，对于搅拌头与待焊板材之间的热量产生以及热传导均有一定影响。由于上述原因，此3 种连接工艺参数对连接区质量有着十分重要的影响，且3者存在一定的交互作用，因此对该3种工艺参数进行优化。

连接参数对抗拉强度的交互作用图如图3 所示，图3（a）和（b）为抗拉强度与前进速度、搅拌头转速的等值线图和曲面图，其等值线图呈椭圆形，曲面图搅拌头转速方向上的曲率更大，该两种工艺参数中搅拌头转速对连接区抗拉强度的影响较大。图3（c）和（d）为抗拉强度与下压量、转速等值线图和曲面图，等值线图中图形呈圆形，曲面图中曲面呈较为圆滑的曲面，该两种工艺参数对于抗拉强度的相应程度相似，均能产生较大影响。结合图3（a）、（b）、（e）、（f）可知前进速度对抗拉强度的影响小于下压量及转速。3 对工艺参数的等值线及曲面图都呈现出明显的上升及下降趋势，其中下压量与搅拌头转速的曲面图曲率更为明显，代表该两种参数度对抗拉强度影响更大。随着工具旋转速度、连接速度和下压量的增加，抗拉强度逐渐升高到最大值，随后下降。搅拌摩擦热输入较高的工艺参数组合会导致连接区中心晶粒尺寸增加，热影响区及热机械影响区的，沉淀相发生粗化和溶解，使接头性能降低。较低搅拌摩擦热输入的工艺参数组合，会使材料无法充分流动，导致连接区易产生缺陷。在拉伸试验中，缺陷是断裂开始的主要部位，缺陷极大地影响了抗拉强度，致使其显著降低。

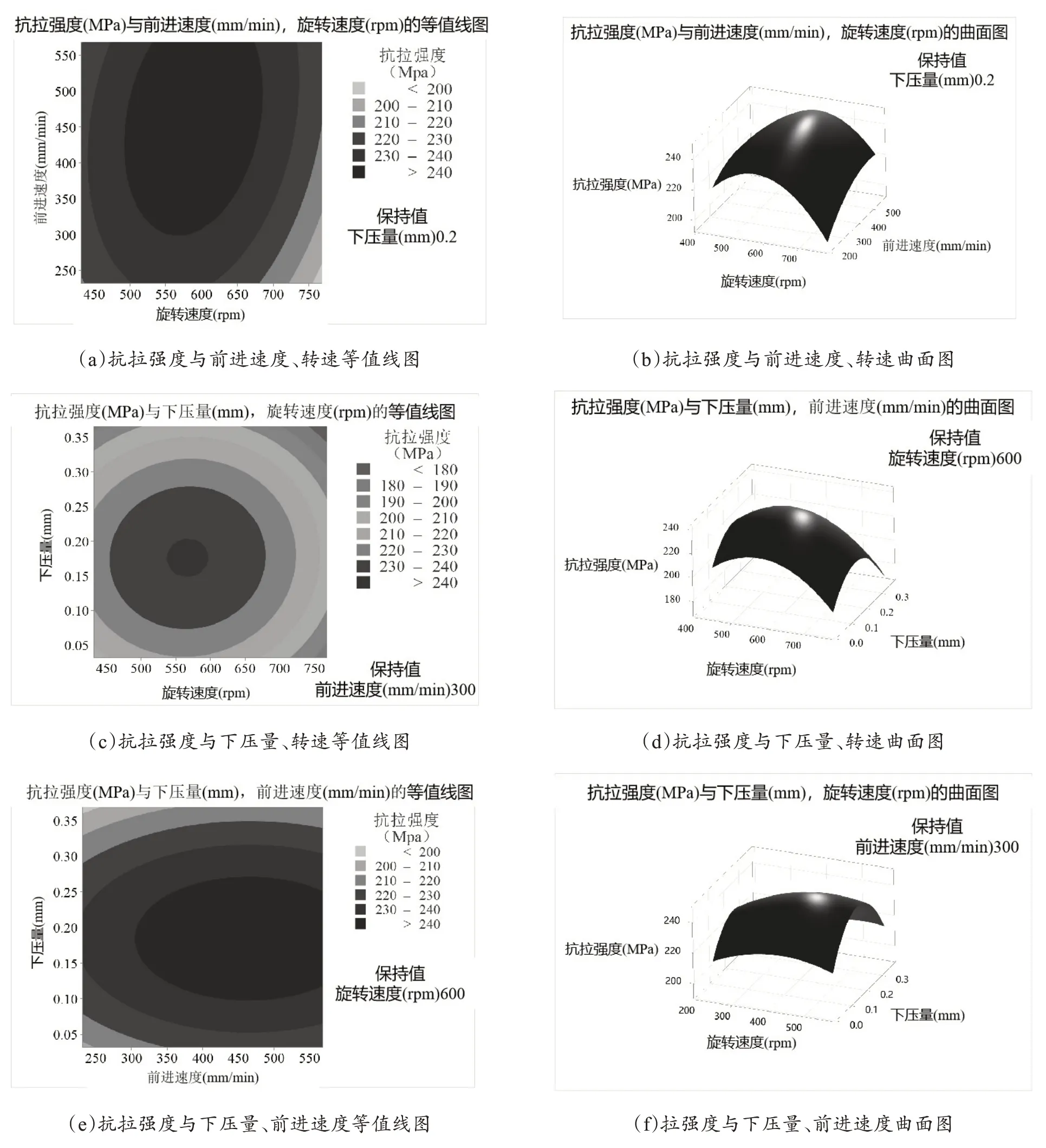
图3 连接参数对抗拉强度的交互作用图

2.3 工艺优化

利用响应面法在分析连接参数对连接区抗拉强度影响趋势的同时，还可以通过Minitab Statistical Software 求解中拟合出的三元二次方程得到最佳工艺参数。结果表明在本研究给定的参数范围内，在搅拌头转速为588rpm、连接速度为459mm/min、轴肩下压量为0.184mm 的条件下抗拉强度取得极大值拟合的预测区间为243Mpa 到253Mpa 之间。进行最佳工艺条件下异种铝合金搅拌摩擦连接试验验证，试验测得抗拉强度结果为252Mpa，其拉伸测试结果如图4 所示，与软件模拟结果基本相同。

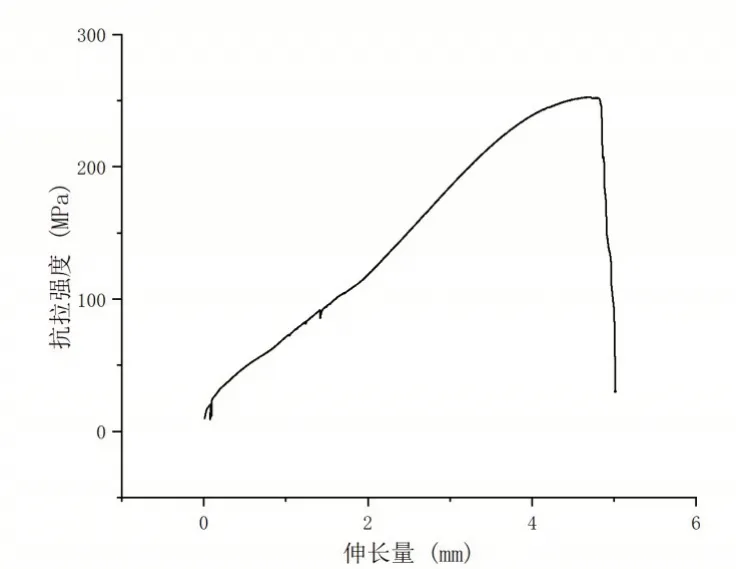
图4 最佳工艺参数下抗拉强度测试结果

3 结 论

1.构建了2A12/6061 异种铝合金FSJ 工艺参数（搅拌头转速、连接速度、下压量）与抗拉强度的数学模型，并通过方差分析来分析模型显著性。

2.在搅拌头转速、连接速度、下压量对接头抗拉强度影响中，连接速度对接头力学性能影响较小，搅拌头转速与下压量对其作用能力相当。

3.通过建立的数学模型对工艺参数进行最优化分析得：当搅拌头转速（A）、连接速度（B）、下压量（C）分别为590rpm、460mm/min、0.184mm 时抗拉强度达到最大值252MPa，处于数学模型预测区间。