一种防震荡的机器人路径规划算法

伏明兰，万宇杰

(淮北师范大学计算机科学与技术学院，安徽 淮北 235000)

0 引 言

移动机器人的路径规划问题是指如何在有障碍物的工作环境中，找到一条从给定起点到终点的最优路径，使机器人能够安全绕过所有障碍物而不发生碰撞，且路径长度最短。路径规划算法一般分为全局规划和局部规划[1]。在全局规划中，机器人根据全局环境信息一次性规划出从起点到终点的安全路径。当环境中只有静态障碍时，该问题又称为基于静态信息的全局路径规划问题。针对该类问题，有很多解决方法，而由于该问题属于NP 难题，所以基于启发式策略的路径规划算法得到了广泛研究，包括遗传算法[2]、粒子群算法[3，4]、蚁群优化算法[5，6]，以及上述各种算法的融合[7，8]。然而这些算法用在机器人路径规划中容易出现震荡问题[9]，为了克服该问题，在“基于静态信息的全局规划算法”的基础上，改进蚂蚁选择下一步栅格的决策策略，使之能尽快绕开障碍物，朝着目的地前进。

1 问题描述

M.B.Metea 首次提出栅格法并用于求解分级地形的自动化路径规划问题[10]。需要解决的问题描述如下[5]：

对于给定的基于栅格模型和静态全局信息的二维环境，机器人R的起点为gbegin，目的地为gend。机器人R在二维环境中的运动区域为有限的凸多边形，记为AS，其边界默认为障碍物，内部分布着的静态障碍物记为Sb1,Sb2,…,Sbn。以AS左上角为原点建立直角坐标系Σ0。并以Ra为步长将X，Y分别进行划分，由此形成一个个栅格，如图1所示[5]。

图1 栅格坐标模型

AS区域内静态障碍物所占栅格的集合记为OS={o1,o2,…,om}∈A(m≥n)。AS内剩余栅格所组成的集合称为可移动区域，记为A。g∈AS的坐标记为g(x,y)。栅格序号集记为C={}1,2,…,M，序号与栅格坐标的对应关系如图1 所示。机器人R在t时刻的位置记为PR(t)=(xR(t),yR(t))。为了描述问题方便，本文对其他一些符号做了约定。

定义1[5]：anti={1,2,…,k,…,m}表示第i 个蚂蚁家族(i= 1,2)，eij表示gi和gj之间的连线。τij(t)表示在t时刻边eij上的信息素。蚂蚁k在ti时刻的位置记为P(xi(ti),yi(ti))，简记为Pi或P(ti)。相邻栅格gi和gh之间的距离为1或，因此定义蚂蚁在gi处的视野域为：

定义2[5]：在时刻ti，蚂蚁k在gi处的可行域为：Wki(gi(xi,yj))={g|g∈BRi(gi(xi,yi))，g∉OS,i∈C}；禁忌表包含所有已走过的栅格：tabuk={P(t0),P(t1),…,P(ti)}。

定义3[5]：蚂蚁选择gi的启发函数如式（1）所示（其中D为常数）：

其中，K∈{1,2}表示蚂蚁家族的编号。

定义4：在ti时刻，蚂蚁k到目标栅格gend(xend,yend)的向量v可用式（2）表示：

其中(xk,yk)代表蚂蚁k当前所在栅格的位置坐标。v和向量（1,0）的夹角θ的计算如式（3）所示：

2 改进的基于静态信息的全局规划算法

2.1 基于蚁群算法的全局路径规划算法描述

在此首先给出经典的“基于静态信息的全局规划算法”，称为“算法1”的描述[5]。因为蚂蚁家族ant1和ant2的区别只在于出发点和目标点不一样，其他基本思想都一样，所以算法描述过程只考虑ant1中的蚂蚁。算法的步骤描述如下：

步骤1：初始化禁忌表tabuk(k= 1,2,…,m) 为gbegin。τij(0) ←τ0（τ0为常数）。初始化迭代器nc、m和最大代次数MaxNc的值，其中m≤4。

步骤2：∀k∈ant1以当前栅格gi为中心，i∈C，按下述步骤选择下一步要走的栅格gj，gj∉tabuk：

(1)若gj∈BRbegin(gbegin)，对于i,j= 1,2,…,m，则，且。其中上标ki和kj表示不同蚂蚁选择不同的栅格。

(2)若gi∉BRbegin(gbegin)，∀k根据式（4）和（5）选择gj∈Wki(gi)，gj∉tabuk。

其中S为按照概率随机选择的栅格的编号；q为随机数，0 ＜q≤1；q0和β为常数。

步骤3：按式（6）更新边eij的信息素。

当τij(n+ 1) ＜τmin时，令τij(n+ 1) =τmin。

步骤4：如果有蚂蚁相遇，则执行步骤5，否则令i=j，并返回步骤2，直到有蚂蚁相遇或所有栅格都选择完毕或有蚂蚁直接到达了目标栅格。

步骤5：连接相遇蚂蚁所经过的路径，计算路径长度，并记录最优路径。

步骤6：按式（7）对全局信息素进行更新：

步骤7：更新nc的值，若nc＜MaxNc，则重新初始化禁忌表，重复步骤2至步骤7，直到nc=MaxNc。

2.2 算法1中的震荡现象

当障碍物比较大，而目标栅格在障碍物的后面，此时依照算法1进行路径规划，就容易出现震荡现象，比如图2所示情形。

图2 静态障碍栅格设计

图2 所示是一个20×20 的有限运动区域AS，黑色栅格为静态障碍栅格。gbegin=g25为出发栅格，gend=g211为目标栅格。在此障碍栅格的设置情况下，利用算法1求从gbegin到gend的最优路径。

仿真环境为PC Intel 2.4GHz，1G。算法1各参数设置如下：m= 3，τ0= 2.0，D= 20，q0= 0.8，β=2.0，ρ= 0.05，Q1= 20，α= 0.05，Q2= 20，寻食最大代数为100，仿真结果如图3所示。

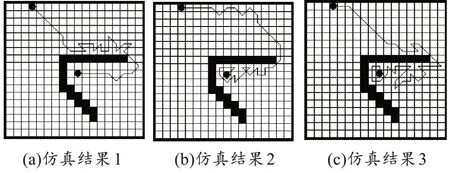
图3 算法1仿真结果

由仿真结果可以看出，当蚂蚁绕过较大障碍物时发生了震荡。其原因是蚂蚁在选择下一步栅格时，除了考虑信息素的大小，还需考虑当前栅格离目标点的距离。

假设当前栅格gi的邻域栅格编号如图4 所示。从图5 可以看出，当蚂蚁移动到C 点(gi=g153)时，其所有的可行栅格中，1号栅格相对于4号栅格离目标g211更近，根据算法1，选择1号栅格的概率更大。但由图5 可知，要尽快绕过障碍物，4 号栅格优于1 号栅格。为了解决该问题，在此规定一个检查顺序，比如在图5 中当蚂蚁k来到C点时给定其检查顺序orderk={6,5 or 7, 4 or 8, 3 or 1,2}（iorj代表随机选择先检查i号或j号邻域栅格）。该顺序只在蚂蚁第一次遇到该障碍物的时候计算，其计算过程称为“过程1”，分为如下3步：

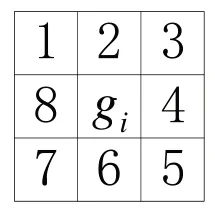
图4 gi的邻域栅格编号

图5 蚂蚁的移动位置示例

（1）求当前栅格gi到目标栅格gend的向量v；（2）根据公式（3）求向量v和向量（1,0）的夹角θ；（3）根据θ的取值，从表1中获得邻域栅格查找顺序orderk。

表1 根据θ得领域栅格查看的顺序

本文的算法称为“算法2”，主要对算法1的步骤2 做了进一步改进，其他的步骤类似，故算法2 只对步骤2进行描述：

（1）设obs←0，值为0 代表蚂蚁k在上一步中选择的优先栅格是可行点。

（2）当q≤q0时，根据下面的“过程2”选择下一步栅格gj（蚂蚁k的当前栅格记为gi，要选择的下一个栅格记为gj）：

过程2：选择下一栅格的策略

1.计算下一步优先选择的栅格：

2.IF(gfirst为可行节点)

蚂蚁进入该栅格，令gj=gfirst。

3.ELSE IF(obs= 0)

当遇到新的障碍物时，调用过程1重新计算orderk。按照orderk定义的顺序，依次检查邻域栅格是否为可行点。gj的值即为第1次检测到的可行栅格的编号。并记obs=1。

4.ELSE IF(obs= 1)

按照原有orderk定义的顺序，依次检查邻域栅格是否为可行点。gj的值即为第1次检测到的可行栅格的编号。并记obs= 0。

（3）当q＞q0时，蚂蚁k按照式（5）定义的概率随机选择下一步要走的栅格序号gj。

3 改进后算法2的仿真实验

仿真1：参数设置同2.2 节。算法1、算法2 运行20次，迭代次数都设为100。算法1和算法2得到的最优路径的平均长度分别为35和26。

算法2 的仿真结果如图6 所示。 其中gbegin=g25，gend=g211，图6（a）、图6（b）和图6（c）所示路径的长度分别为27、24和28。由仿真结果可以看出，当蚂蚁遇到较大障碍物时，算法2能较快地避开障碍物，得到一条更短的路径。

图6 算法2仿真结果

仿真2：目标值设为26，算法1 和算法2 分别运行6次。两种算法达到目标值时的迭代次数和所用时间如表2所示，时间单位为毫秒。

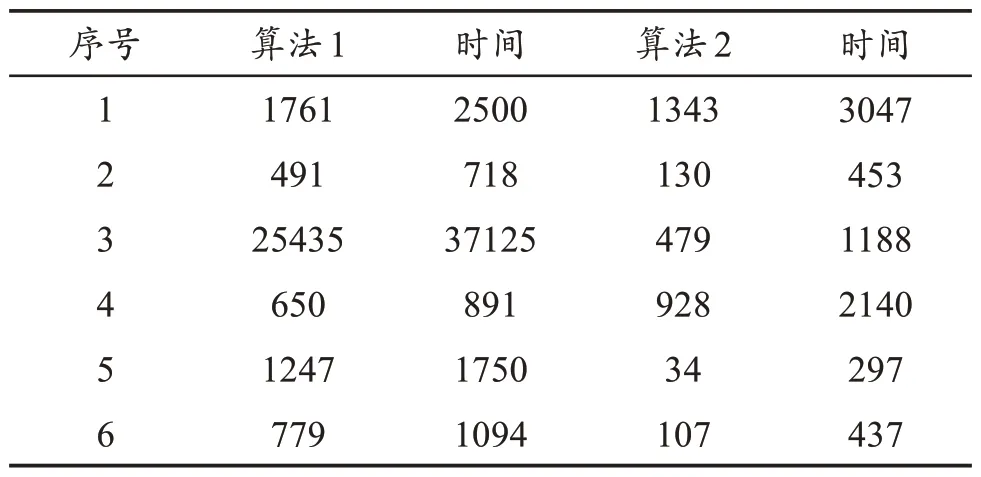
表2 迭代次数和运行时间比较

由表2 可见，在大多数情况下，算法2 所需的迭代次数和运行时间要少于算法1。

4 总 结

本文在基于静态信息的路径规划算法的基础上，改变蚂蚁选择下一步栅格的策略，从而有效克服了路径规划中的震荡问题。本文算法还有需要进一步改进的地方，比如当蚂蚁绕开障碍物时可以将当前栅格和绕开上一障碍物的栅格之间的曲线拉直，该问题可由Bresenham 算法解决[11]，这些都在进一步的研究和实现中。