多模态声驻波场的探究

朱彦达,吴苜饶,符维娟

(复旦大学 物理学系,上海 200433)

驻波现象广泛存在于日常生活及实际应用中,很多形式的波在一定条件下都能形成驻波现象,例如绳上的机械波在端点反射后干涉形成可见的驻波现象[1],在演奏管乐器时通过在管中形成驻波从而发出悦耳的声音[2],激光器的制作过程中让电磁波在谐振腔中干涉形成驻波[3]等. 因此,研究驻波现象的形成过程、物理机制和应用具有重要意义. 大学物理教学中,驻波通常作为特别的干涉现象设置在振动和波动章节后,课堂教学中也常采用驻波演示实验. 文献[1]中采用圆偏振波演示实验仪演示两端固定的一维弦线在不同模态下的驻波形态;文献[4-5]中的声驻波演示仪采用一定长度的圆形驻波管,借助雾滴、声控二极管等演示驻波场的空间分布,但是媒介的离散性以及能量的损耗的影响使得管中驻波现象的空间连续性不如弦线驻波.

本文设计并搭建多模态声驻波演示仪,可以通过自动扫频测量驻波管的实际模态频率,再通过自动扫场测量各个模态下的声驻波场分布,并实时监听驻波场内部的声音;还可探究边界条件对声驻波场的影响,并观察声场的非线性特征.

1 演示实验装置的设计

多模态声驻波演示仪的装置设计如图1所示,主要包括激励端(喇叭)、驻波管(有机玻璃管)及信号采集端(放置于移动滑台上的麦克风),麦克风和喇叭均连接到电脑.

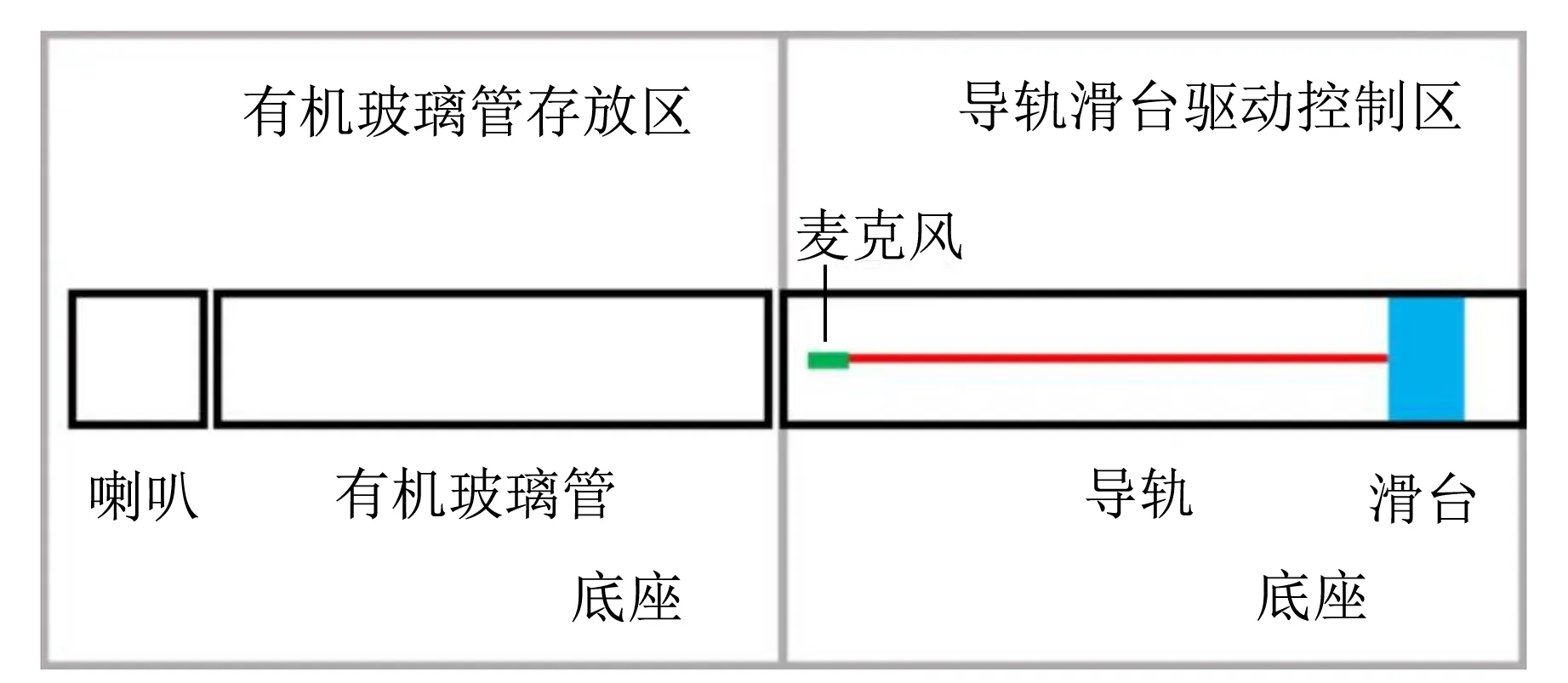
图1 多模态声驻波演示仪装置设计图

多模态声驻波演示仪的实物装置如图2所示,音源喇叭封装在黑色的3D打印组件中,角铝支架上可放置不同长度和半径的亚克力驻波管,末端装有微型麦克风的碳纤维管用3D打印组件架在滑台上,滑台为LD45同步带导轨滑台套装(由有效行程为500 mm的导轨滑台、控制器、驱动器等组成),实验装置固定于防震的木制底板上.

图2 多模态声驻波演示仪实物装置图

1.1 激励端

激励端为外径5.5 cm的纸盆喇叭,采用Audition音频分析软件制作了不同的音源文件,随时间均匀升高的音调用于扫频测量,单频声音用于扫场测量,音源的强度保持恒定. 需要注意的是,喇叭实际输出的声音与Audition设置的声音之间存在差异. 例如,Audition设置输出正弦波,采集到的喇叭输出声音波形偏离正弦波,其频谱中可观察到高次谐频.

1.2 驻波管

亚克力驻波管如图3所示,有32cm和48cm2种长度;2种管径(外径5.5 cm/内径5.2 cm,外径5.5 cm/内径1.8 cm). 此外,还制作了3D打印的PETG材料反射界面,如图4所示.

图3 亚克力驻波管

图4 反射界面

1.3 接收端

选用直径较小的驻极体麦克风,减少麦克风端面反射对管内声场的影响. 该麦克风具有较好的指向性,能够减小管壁反射对声场探测的影响. 麦克风置于碳纤维管末端,与导轨滑台的连接部件由3D打印制作,采用类似于光具座的结构实现麦克风的高度调控.

LD45同步带导轨滑台套装的导程为75 mm/r,其主要可调参量包括:电机电流、驱动电机转1圈对应的脉冲数以及单位时间输入的脉冲数. 其中,电机电流决定了电机的扭矩. 脉冲数决定了滑台的移动速度,如果速度过小,则扫场测量时间太长;如果速度太大,则驻极体声传感器的响应不够. 本实验系统负载较小,电流调至最小0.50 A. 其他参量设置为:5 000 r-1,400 s-1,滑台以6 mm/s的速度匀速自动移动.

麦克风采集到的声音信号输入Audition实时显示时域波形,经短时傅里叶变换(Shorttime Fourier transform, STFT)得到的频谱(FFT大小为8 192,窗口为汉恩)提供了驻波管中某点声场的频域信息. 同时,还对驻波管内部声场进行同步监听并以蓝牙音箱实时外放.

2 实验方法

2.1 固定位置下的扫频测量

利用Audition制作在200～3 200 Hz范围内频率均匀增加、总时长为30 s的扫频音源,将麦克风放置于驻波管(长度为32 cm、内径为1.8 cm)的管口,并播放扫频音源. 管口处测得的声音波形如图5所示,图中若干个峰对应了驻波管的共振响应,峰处的频率为驻波管的模态频率. Audition频率分析窗口(图6)显示了图5中指针(红色竖线)处的STFT频谱结果,图6中可见基频和谐频,读出基频数值约为1 439 Hz,即为相应的驻波管模态频率.

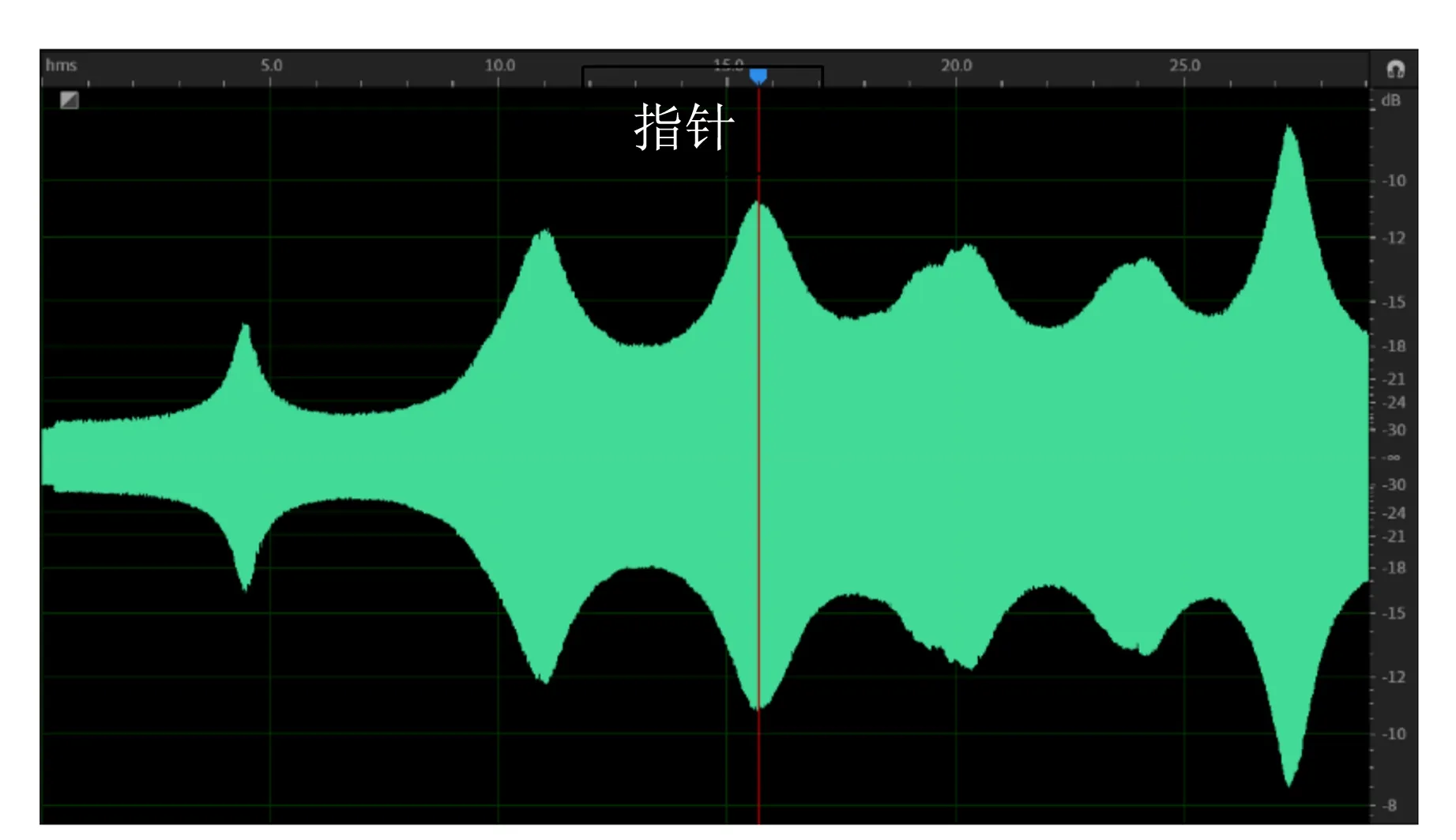
图5 驻波管管口处扫频测量结果图

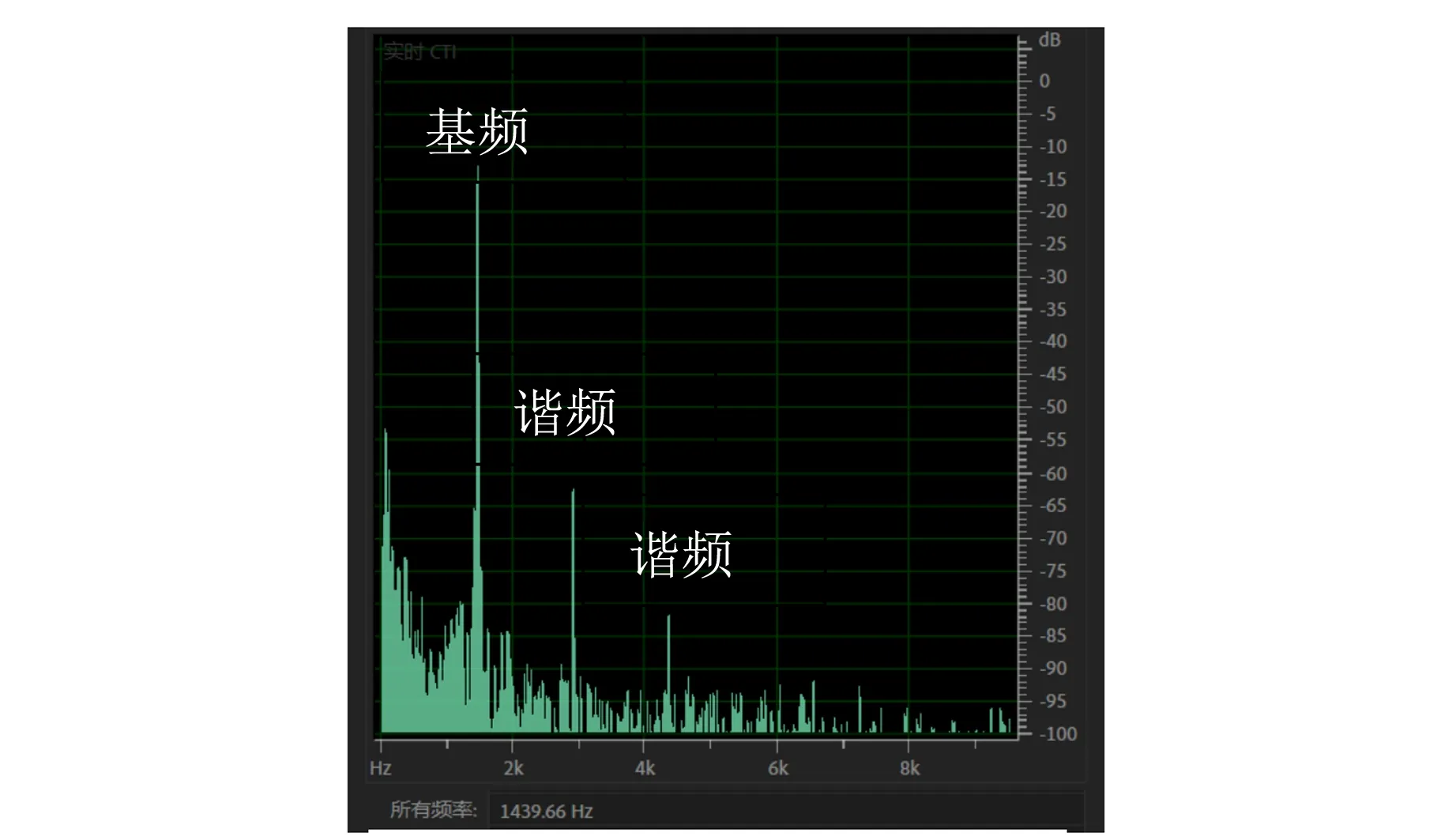
图6 STFT频率分析窗口

2.2 固定频率下的扫场测量

将音源设定为单一频率的正弦波,编写程序控制滑台自动移动,使麦克风沿着驻波管轴向进行扫场测量,结果如图7所示,横轴为时间,纵轴为声强. 测量过程如下:打开音源(A)→麦克风从管外向管内移动→麦克风进入管内(B)→麦克风将要碰到喇叭时停止移动(C)→麦克风从管内快速向管外移动(D)→回到原位并停止(E).因此,BC段为靠近音源的慢速扫场结果,DE段为远离音源的快速扫场结果.

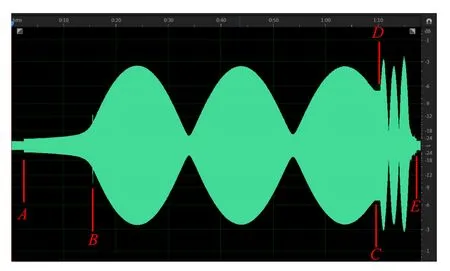
图7 驻波管轴向扫场测量结果图

3 有限长圆管中的声驻波物理模型

3.1 单模态的空间驻波图像

平面声波在有限长的均匀管中传播,若末端管口处存在不均匀界面,即为声负载,一部分声波被负载吸收,另一部分则被负载反射,与管中原始声场叠加[6]. 将原点取在末端负载处,入射波与反射波的形式分别为

(1)

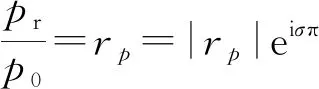
入射波和反射波叠加得到管中的总声压为

p(x)=pi+pr=|pa(x)|ei(ω t+φ),

(2)

总声压振幅为

|pa(x)|=

其中,φ为引入的固定相位.长为L的圆管中,声波在反射率分别为r1和r2、反射相位为σπ的前后端界面间多次反射,管内的总声压

(3)

由式(3)可以看出,驻波振幅由反射率与反射相位共同决定,由此反射界面的性质也是影响驻波管模态的重要因素.将驻波管的共振频率定义为使驻波的最大振幅取极大值的频率,此时波数满足

(4)

(5)

式中,c0=340 m/s为管内空气中的声速.在某个共振频率下平面声波在驻波管内形成相应模态的驻波场,因此共振频率也称为模态频率.

若采用p(x)=Acos (kx+φ)cos (ωt+ψ)作为驻波解[7],并结合反射条件可以得到与式(5)形式相同的共振频率结果.

3.2 驻波图像的精细结构

图6显示驻波场中某点的STFT频谱存在谐频,因此圆管中的声驻波不仅包括声源输出基频的驻波场,还包括高次谐频的驻波场. 由于不同频率的驻波场在空间的分布不同,而且高次谐频的声强比基频小,所以将其称为驻波场的精细结构.

上述讨论中描述声压的方程为线性方程,其满足的前提是声波振幅不太大,空气密度视为常量.当声波振幅较大时,空气密度不可看作常量,空气质量元的运动方程为

(6)

式中,η为黏度.假设此时空气仍满足流体连续性方程与绝热方程,一维行波的速度与密度波动方程应修改为

(7)

由于速度波和密度波具有固定的相位差,有

(8)

于是行波的速度波满足

(9)

当声源为简谐振动时,式(9)的1个特解为

(10)

对该特解做线性展开,可以得到

(11)

由式(11)可知,谐频与基频的强度正相关,在声场强度较小时,谐频相对基频成分为小量,谐频强度随传播距离的增加而增大,从而产生了随传播积累的非线性效应.

4 实验结果与讨论

4.1 模态频率与单模态驻波

为了获得驻波管的模态频率,采用2.1描述的扫频法对驻波场中的固定点进行测量. 驻波管的外径为55 mm、内径为18 mm,驻波管末端为开口,分别对L=32,48 cm的驻波管端口场点进行扫频测量,结果如图8所示.

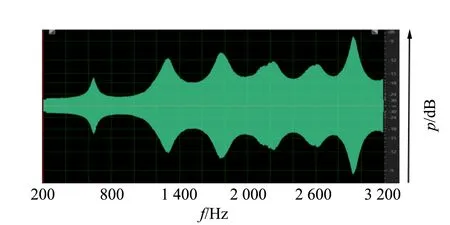
(a)L=32 cm的扫频结果

图8中可见若干个显著波峰,对应了驻波管的模态频率,通过Audition获取各个峰处的频率值,结果如表1所示.

表1 不同管长驻波管的模态频率

表1中,长驻波管的模态频率较短驻波管小,符合式(5)中模态频率随管长的变化规律,各模态频率测量值与式(5)理论计算值存在10%～20%的偏差.

选取L=32 cm的驻波管,末端开口,采用驻波管的第2和第3个模态频率(1 016 Hz与1 454 Hz),制作单频正弦波扫场音源,根据2.2描述的扫场法对管内驻波场进行扫场测量,结果如图9所示.

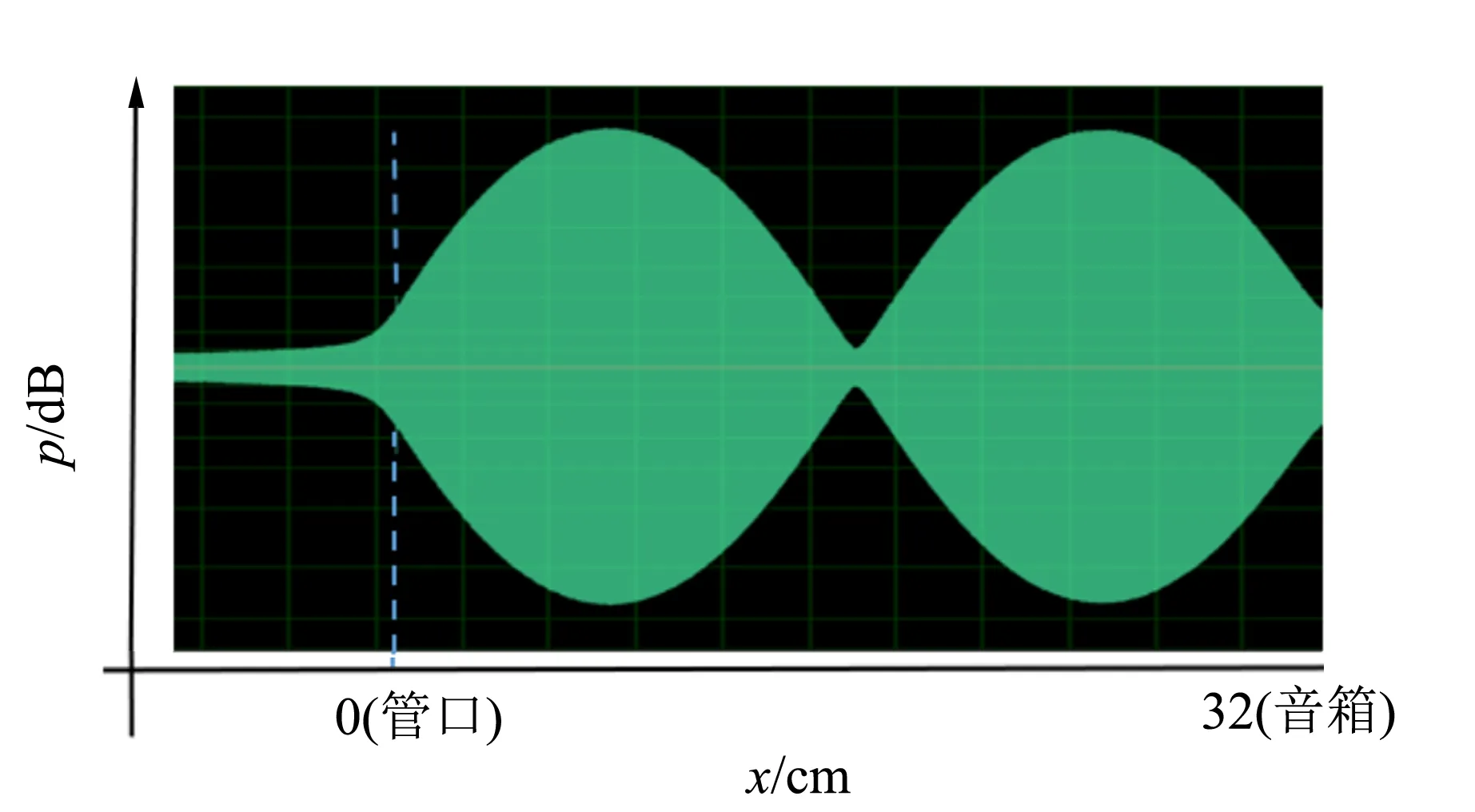
(a)1 016 Hz模态的驻波场

图9为连续的驻波形态,读取1 016 Hz和1 454 Hz的驻波波长分别为16.6 cm和11.7 cm,相应的声波波长分别为33.5 cm与23.4 cm,在误差范围内满足2倍驻波波长等于声波波长,符合3.1节中的界面反射理论.

将音源改为同振幅的非模态频率(1200Hz)正弦波声音,与模态频率(1 454 Hz)音源扫场结果的对比如图10所示,2种音源的频率差异较小,音源输出的频率响应差异可忽略.

图10中非模态频率音源下的管内声场仍有驻波场特征,驻波波长为声波波长的1/2,与模态频率一致,但是波腹处的振幅显著小于模态频率. 由于实际音源产生的波并非理想平面简谐波,从而使得驻波管的模态频率理论计算值[式(5)]和实测值(表1)存在偏差. 根据图10的对比结果可知,采用扫频法测得模态频率,并用模态频率音源激发驻波管,才能得到最大的驻波振幅,达到驻波管的共振状态. 因此,扫频法是获取驻波管模态频率真值的有效实验方法,也为式(5)理论计算的修正提供了依据.

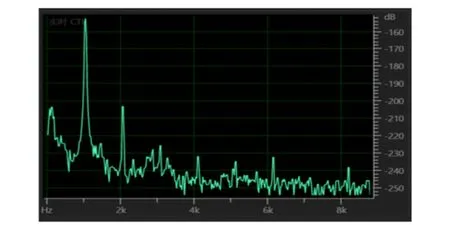
图10所示的单模态驻波场图像中,波节的振幅并不为零,其可能原因为开口端界面反射率并不为1. 此外,图6显示了驻波场中存在谐频,为了确定谐频是由驻波管的非线性效应产生还是由音源喇叭产生,对开放环境中距离音源喇叭2 cm处的场点进行了测量,其频谱如图11所示.

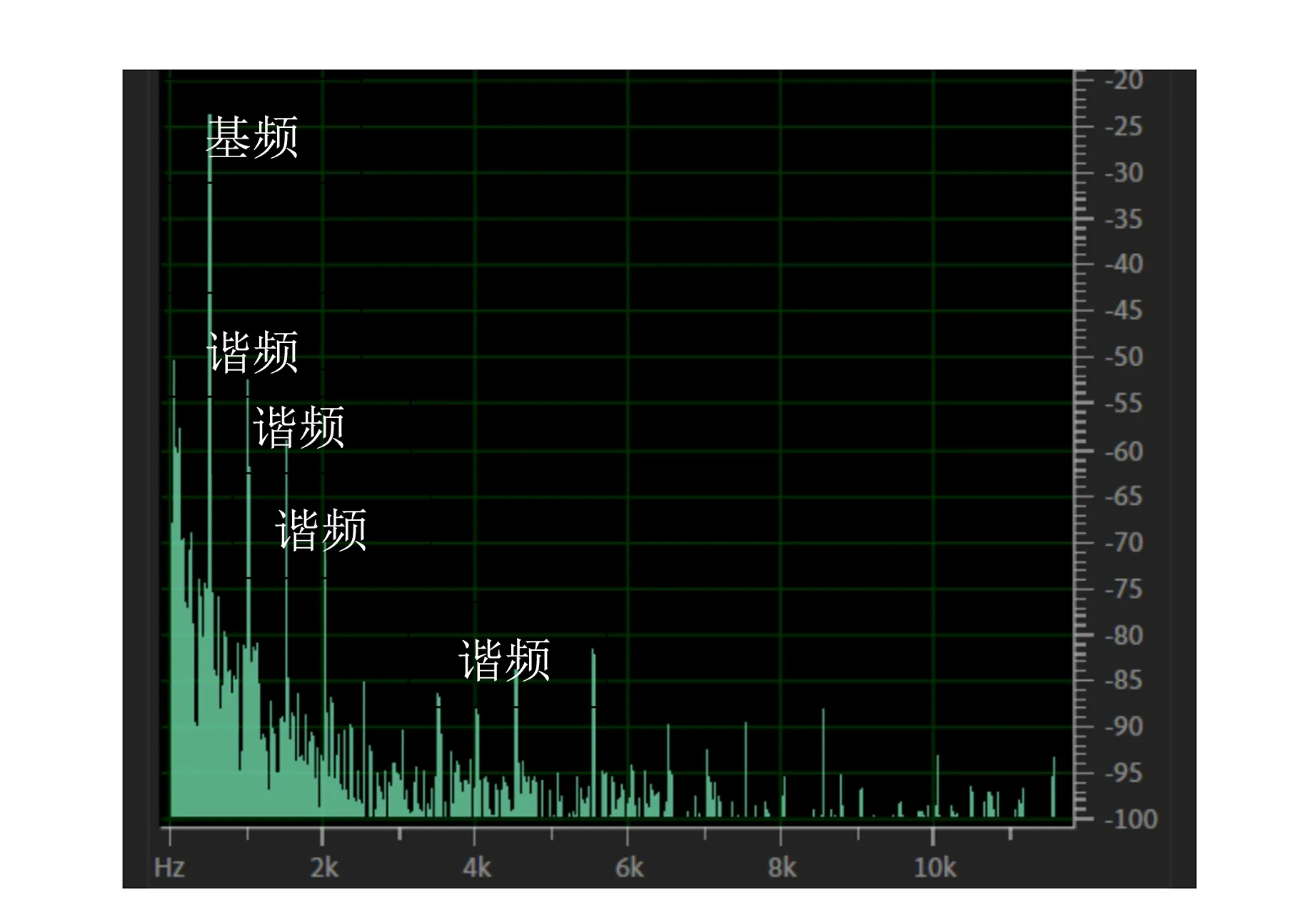
图11 音源喇叭实际输出声音的频谱(500 Hz正弦波)

图11中,音源设置为500 Hz的正弦波,实际输出除了500 Hz的基频外,还包含高次谐频,这是喇叭自身的非线性效应所致. 因此,驻波管中基频和各次谐频驻波场叠加形成复杂的空间声场,通过频谱图可探究驻波场的精细结构,即各频率的驻波场.

图12是模态频率(1 016 Hz)下波腹和波节处的频谱图,波节处的声强由基频和谐频共同组成,波节处的谐频成分比波腹处更为显著. 因此,界面反射率和谐波共同使得波节处的声强不为零. 图12显示谐频成分相对基频较小(纵坐标单位为dB),仅做声驻波场空间图像演示时仍可近似认为是管中为基频单模态空间驻波场.

(a)波腹处的频谱图

4.2 界面对模态频率及反射相位的影响

为了演示边界条件对驻波管末端反射相位的影响,在L=32 cm的驻波管末端放置刚性界面(3D打印制作的PETG塑料挡板). 对开口界面和刚性界面下的驻波管端口处分别进行扫频测量,结果如图13所示.

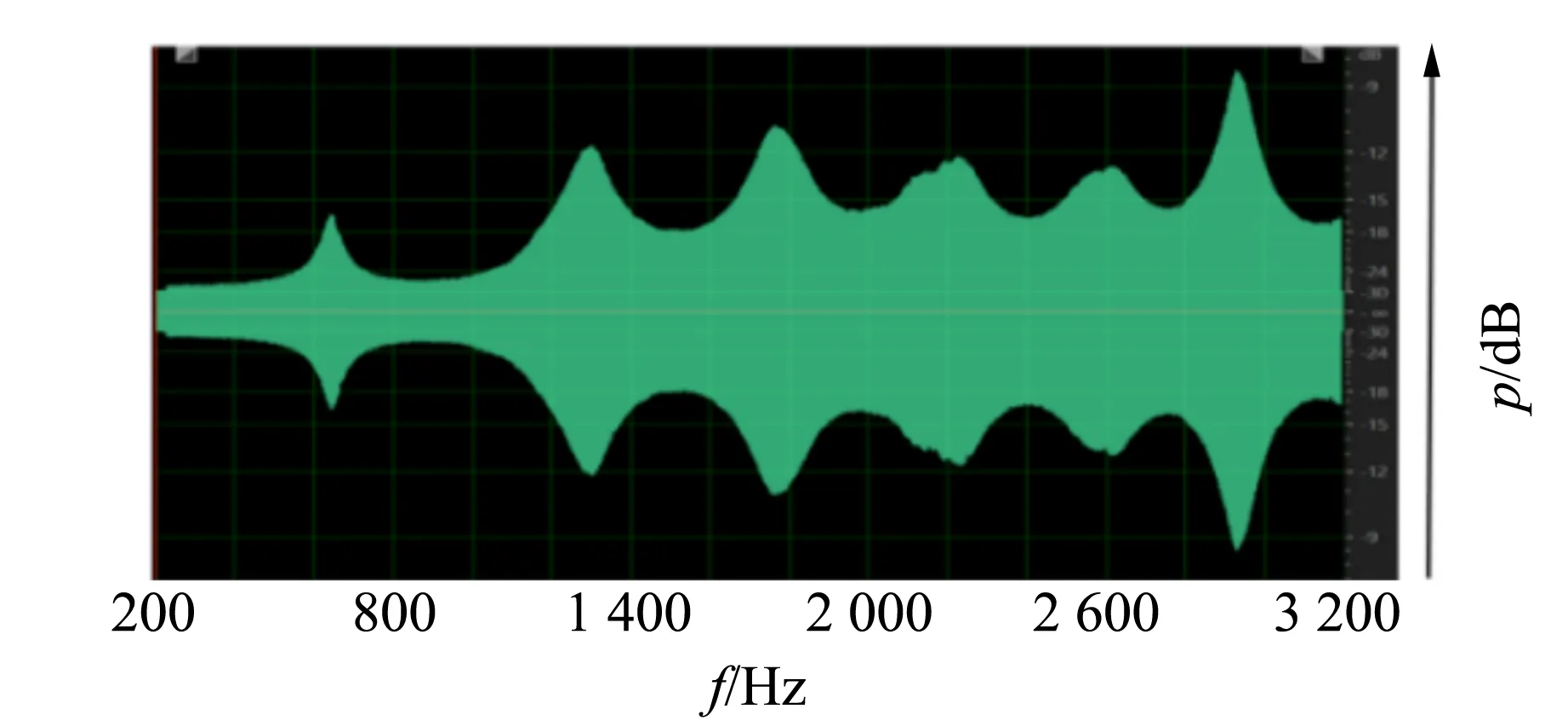
(a)开口界面的扫频结果

用Audition读取图14中的驻波管模态频率数据,如表2所示.

表2 开口/刚性界面下的模态频率比较(L=32 cm)

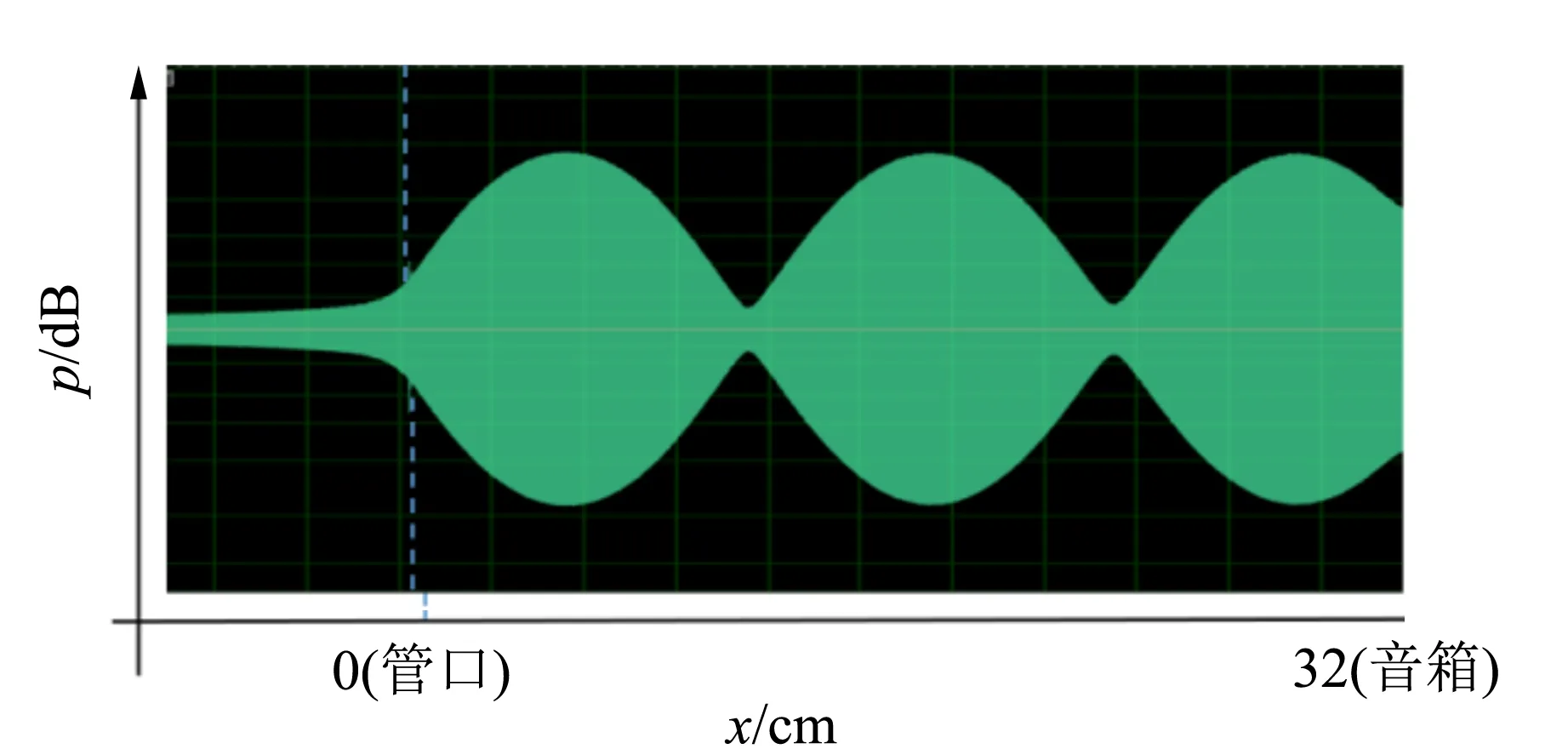
(a)开口界面的驻波图像

根据表2中的数据,用1 454 Hz模态频率音源激发末端为开口界面的驻波管,用1 712 Hz模态频率音源激发末端为刚性界面的驻波管,扫场测量结果如图14所示.

再用非模态频率(1 200 Hz)音源对开口界面管与刚性界面管进行扫场测量,结果如图15所示.

(a)开口界面的驻波图像

由图14和图15可知,模态频率和非模态频率音源激励下,刚性界面均靠近驻波场波腹位置,开口界面均靠近驻波场的波节位置. 驻波管末端为波腹还是波节由反射相位决定,反射相位又由反射界面决定,因此通过驻波图像可以推断反射界面的声学特性.

开口界面处靠近波节位置,存在半波损失,反射相位为π,因此开口界面的反射为波疏(管内空气)到波密(开放环境空气)介质反射. 刚性界面处靠近波腹位置,反射相位为0,因此刚性界面的反射为波密(管内空气)到波疏(刚性界面)介质反射. 不同于光(电磁波)在空气-有机玻璃或塑料界面反射时认为空气是波疏介质、有机玻璃或塑料为波密介质,机械波在空气中的波速比在有机玻璃或塑料中快[4]. 文献[8]中也指出刚性界面与开口界面的反射率均可看作为1,反射相位分别近似为0(刚性)和π(开口).

4.3 实验装置结构参量对演示效果的影响

为了考察麦克风端面的反射对管中驻波场的影响程度,分别用直径为8 mm和4 mm的麦克风对长度为32 cm、内径为18 mm和51 mm的驻波管,在1 000 Hz频率音源激励下进行扫场测量,结果如图16所示.

(a)φ4 mm麦克风的驻波场

图16显示φ8 mm的麦克风扫场得到的驻波场图像波腹两侧明显不对称,而φ4 mm的麦克风的驻波场图像基本对称,由此需要选用直径较小的麦克风.

麦克风移动过快也会引起波形的畸变,图17为麦克风移动速度相差5倍时的扫场结果对比,扫场过快时噪声增加、波形不光滑,减慢速度可以得到光滑的波形. 但是麦克风移动过慢又会使得外放同步监听的声强变化过于缓慢,影响人耳对声音周期性强弱变化的分辨,因此演示实验时需要在波形与声音之间权衡取得最佳的综合演示效果.

(a)移动速度为v/5的驻波图像

为考察驻波管内径对于演示效果的影响,对长度均为32 cm,外径均为55 mm,但内径分别为18 mm与51 mm的2种驻波管,在1 000 Hz频率音源激励下进行扫场测量,结果如图18所示.

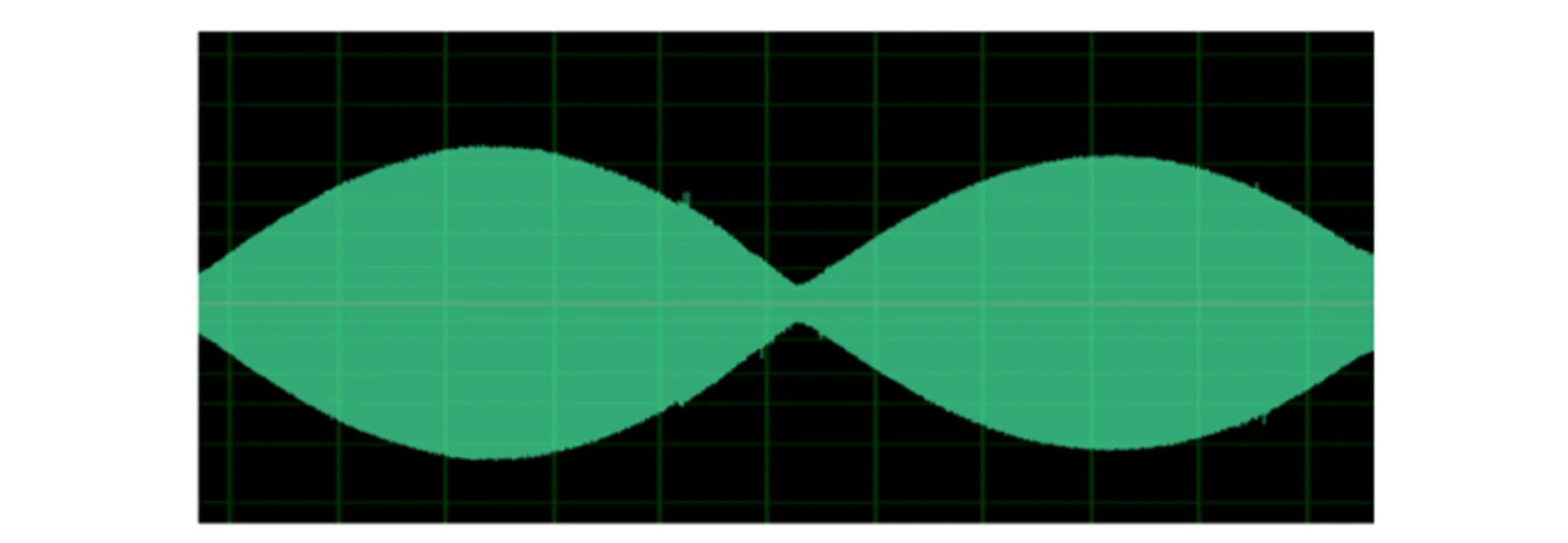
(a)18 mm内径的驻波图像

图18中可见,小内径的管中驻波场更为理想,这是由于小内径管内截取了喇叭原始声场中的近轴部分,是更理想的平面声场. 小内径管中声场能量更集中,声强强度更大,麦克风采集到的声压振幅也更大. 此外,小内径管的末端开口界面处突变程度较大,反射率更接近1,波腹、波节强度差异更明显.

5 结 论

本文设计并制作了具有自动扫频、自动扫场、可变界面以及实时外放监听功能的视听一体的声驻波演示仪,并通过一系列实验确定了具有良好演示效果的结构参量和条件参量. 该演示仪可以通过自动扫频测得声驻波管的实际模态频率,通过自动扫场获取各个模态频率下的声驻波场图像,驻波特性显著、具有良好的空间连续性. 通过驻波管末端呈现波腹或波节来推断反射界面的声学特性,通过频谱图揭示管中声场具有基频和各次谐频驻波场的精细结构. 该演示仪可用于大学物理课堂教学,演示驻波、半波损失、边界条件、谐波、非线性效应等物理概念,也可用于复杂声驻波场的研究.