基于多方安全计算的公共数据融合创新模式研究及应用

金加和，赵程遥，求昊泽，刘鹏

1.浙江省数据开放融合关键技术研究重点实验室，浙江 杭州 310007；2.浙江大学计算机科学与技术学院，浙江 杭州 310027

0 引言

近年来，数据逐渐成为建设数字政府、推动经济社会发展的关键生产要素。数据主要分为公共数据和社会数据。2020年5月，国务院办公厅印发的《公共数据资源开发利用试点方案》中指出，公共数据资源是指由政务部门和公共企事业单位在依法履职或生产活动中生成和管理，以一定形式记录、存储和传输的文字、图像、音频、视频等各类可机器读取的数据。2022年3月1日实施的《浙江省公共数据条例》第三条规定，公共数据是指本省国家机关、法律法规规章授权的具有管理公共事务职能的组织以及供水、供电、供气、公共交通等公共服务运营单位，在依法履行职责或者提供公共服务过程中收集、产生的数据；根据浙江省应用需求，税务、海关、金融监督管理等国家有关部门派驻浙江管理机构提供的数据，也属于公共数据。社会数据则是公共数据以外，企业、机构、协会、个人等社会主体产生的数据。

依据数据的分类，公共数据的融合创新主要面临两大挑战。一是可归集的公共数据和难归集的公共数据之间的融合创新难实现。由于政府规章仅适用于政府部门，人大、党委、政协、检察院、法院等部门的数据难以归集。此外，地方性法规虽然位价高，但在管理海关、税务、电力、银行等国家垂管部门数据时，可能存在相关部门以规章不一致为理由拒绝归集数据的情况。二是公共数据和社会数据之间的融合创新难实现，其中社会数据包含企业、协会、个人等社会主体产生的数据。由于社会数据管理主体缺失，社会数据相关制度规范不完善，数据确权、定价、交易和配置运行等规则制度缺乏，社会数据难以归集和流通利用。公共数据与难以归集的公共数据之间、公共数据与社会数据之间难以整合利用，在一定程度上制约了公共数据领域的数据集聚、倍增和放大效应的产生与价值实现。

多方安全计算技术[1]作为隐私计算的一大技术路线，能实现“原始数据不出域，数据可用不可见”的交易范式，可有效解决公共数据融合创新面临的两大挑战，促进数据再融合、价值再提升。隐私计算的三大技术路线分别为多方安全计算、联邦学习和可信执行环境。联邦学习技术存在隐私信息泄漏的风险，可信执行环境则存在内存受限、依赖于特殊硬件等问题。由于公共数据领域对隐私信息保护的要求极高，多方安全计算技术作为可证安全的隐私计算技术路线最符合公共数据领域。此外公共数据的建模计算过程一般不复杂，也将多方安全计算技术计算效率较低带来的影响降到了最低。多方安全计算在金融、互联网等领域已经得到了广泛的应用，然而在公共数据领域多方安全计算的应用尚不成熟。

基于多方安全计算的公共数据融合创新模式可以借用技术利器破解制度性难题，例如：税务、电力、海关等部门有规章制度不允许数据汇聚整合共享，但是在不触及部门刚性制度的前提下，通过应用多方安全计算技术，可以有效解决这些部门公共数据的融合创新问题，实现数据资源的高效流通和深度开发利用。利用多方安全计算技术，可以使数据一直存在于政务系统的本地数据库中，“数据不出域，可用不可见”，实现公共数据的跨系统、跨应用融合创新；此外，多方安全计算技术能为各政府部门提供统一的数据标准，可以实现在协同计算中的信息检索、查询、数据跟踪等功能，保证数据的安全性、隐私性。基于多方安全计算的公共数据融合创新模式的广泛应用可以直接推进可归集的公共数据与难以归集的公共数据之间、公共数据与社会数据之间的深度融合利用，从而加强数据汇聚融合、共享开放和安全利用，促进数据依法有序流动，激活数据要素价值，助力经济社会高质量发展，加快推进数字政府建设。

1 多方安全计算研究和应用现状

1.1 多方安全计算研究现状

多方安全计算[1]由姚期智教授提出，其主要目标是在无可信第三方的条件下，在利用各方数据得到正确计算结果的同时保护各方隐私信息。通用的多方安全计算协议从实现技术上可以分为：混淆电路（garbled circuit, GC）、秘密共享（secret sharing, SS）、不经意传输（oblivious transfer, OT）以及同态加密（homomorphic encryption, HE）。这些技术可以用来实现多方安全计算核心组件的多方安全计算基础算子层。

混淆电路是用来构建多方安全计算协议的常用方法。姚期智教授首先提出了用于构建多方安全计算协议的姚氏混淆电路[2]。混淆电路将两个参与方的计算函数构建成布尔电路，并将真值表加密扰乱，能在计算正确结果的同时保护双方隐私数据。Lindell Y等[3]则在数学上给出了姚氏混淆电路的完整描述，并严格证明了其安全性。Malkhi D等[4]用程序实现了应用姚氏混淆电路的多方安全计算框架，并实现了通用安全功能评估。Kolesnikov V等[5]提出了网络和电路中几乎全是异或门的混淆电路，并验证了该方法相比于传统混淆电路算法能在保证相同安全性的前提下大大提升计算性能[6]。

秘密共享也是构建多方安全计算协议的常用方法。Beimel A等[7]首先提出了门限秘密共享算法，其中原始信息被拆分，由各参与方管理，单个参与方无法计算原始信息，只有一定数量的参与方协作计算才能得到原始信息。Liu D等[8]提出了基于椭圆曲线的秘密共享算法，利用椭圆曲线的自配对性质提升了算法的安全性和效率。Lin C L等[9]则提出了基于同态加密的秘密共享算法，利用同态加密进一步提升了秘密共享算法的隐私保护能力。

另一构建多方安全计算协议的重要技术是不经意传输。Rabin M O[10]首先提出了不经意传输算法，在该算法中发送方给接收方发送消息，接收方以50%的概率获取该消息，在传输结束后发送方不知道接收方是否获取消息，而接收方能确切地知道是否获取消息。Asharov G等[11]将基本不经意传输算法中的公钥运算转化为椭圆曲线上的公钥运算, 减小了密钥长度，提升了运算速度。Chou T等[12]提出了基于迪菲赫尔曼密钥交换协议和随机预言机模型的不经意传输协议，通过复用传输信息进一步降低不经意传输算法的通信开销。Garg S等[13]提出了基于范围陷门哈希函数的不经意传输算法，大幅降低了不经意传输接收方的通信复杂度。

同态加密技术也可以用来实现多方安全计算协议。Cramer R等[14]基于同态阈值加密系统实现了多方安全计算协议，并证明了其安全性。在乘法同态加密和加法同态加密被提出数十年后，Gentry C等[15]于2009年开创性地提出了全同态加密算法，使数据在加密状态下进行任意计算并解密得到的结果与不加密的数据进行相同计算得到的结果一致。Naehrig M等[16]根据实际场景设计了支持有限同态的同态加密算法，提升了同态加密在实际应用中的效率。Chen C C等[17]则将同态加密算法与秘密共享算法结合，在解决秘密共享算法难以处理稀疏数据的问题的同时，提升了整体加密算法的效率。

1.2 多方安全计算应用现状

随着基于多方安全计算的隐私计算框架不断开源，多方安全计算应用落地得到了技术保障，多方安全计算在金融、互联网等领域已经得到了广泛的应用。在金融领域中，金融机构一般作为数据需求方，通过多方安全计算技术从政府部门、运营商、互联网平台等数据提供方引入外部数据，提升普惠金融[18]、联合风控[19]以及精准营销[18]的效果。在互联网领域中，多方安全计算主要用于在保护用户隐私的前提下提升目标用户推荐和新用户拓展的效率[20-21]，此外还用于增强推荐服务的隐私保护性[22]。

然而在公共数据领域，多方安全计算的应用尚不成熟。目前公共数据的使用已经贯穿于政府管理各个环节，用数据决策、用数据管理、用数据监督已成为常态。针对公共数据领域的数据融合创新问题，本文探讨了基于多方安全计算的公共数据融合创新模式，深入分析了该模式的技术架构，设计了实现该模式的通用流程，最后用具体应用实例加以说明并佐证。

2 基于多方安全计算的公共数据融合创新模式

2.1 公共数据融合创新模式的总体架构

基于多方安全计算的公共数据融合创新模式指基于多方安全计算技术，依托公共数据主管部门，针对可归集的公共数据、难归集的公共数据（税务、海关、电力和银行等）、社会数据，将分散在不同系统域的数据联合计算，从而推动数据资源更好地支撑应用创新，实现效率与价值的最大化。基于多方安全计算的公共数据融合创新模式为3个参与方角色提供操作接口，它们分别为任务调度管理方、数据提供方以及结果使用方。总体架构如图1所示。任务调度管理方一般由公共数据主管部门担任，负责发起联合计算任务，确定各参与方和联合计算算法，并对数据提供方的数据源、结果使用方需要的计算结果以及计算资源进行统一管理，对多任务进行调度。数据提供方和结果使用方都可能有多个，且都由任务调度管理方进行管理。

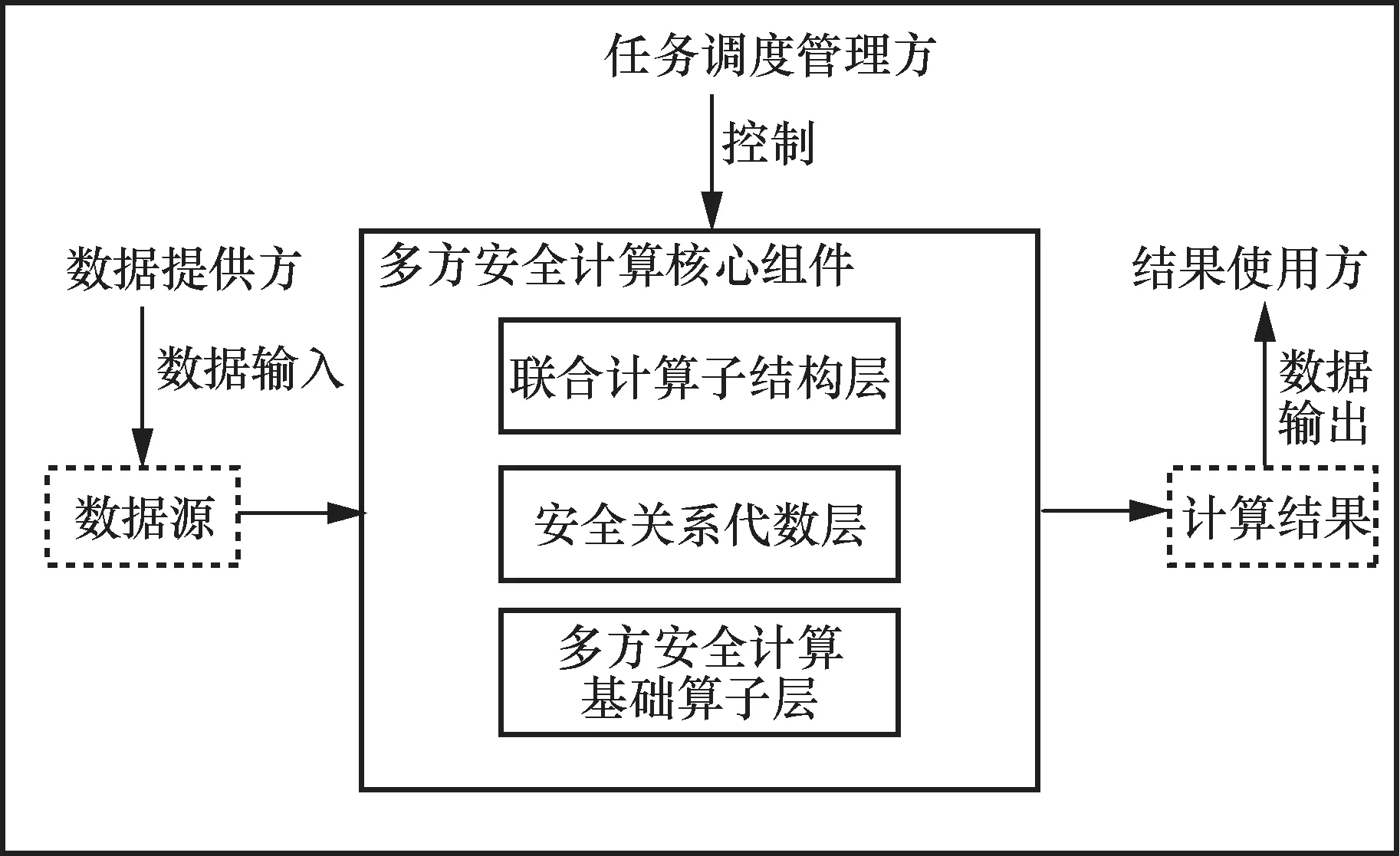
图1 基于多方安全计算的公共数据融合创新模式总体架构

多方安全计算核心组件自底向上被拆解为3层：多方安全计算基础算子层、安全关系代数层和联合计算子结构层，如图2所示。从图2可以看出，多方安全计算基础算子层依赖的是：算术秘密分享、布尔秘密分享、秘密分享比较、秘密分享加法、秘密分享乘法和布尔与算术秘密分享转换。安全关系代数层支持安全求交算法、安全排序算法和安全线性聚合。联合计算子结构层则支持连接、选择、分组和聚合等算法。本节着重研究的是安全关系代数层和联合计算子结构层，并假设已实现底部的多方安全计算基础算子层（多方安全计算基础算子层主要通过第1.1节中的技术手段实现）。

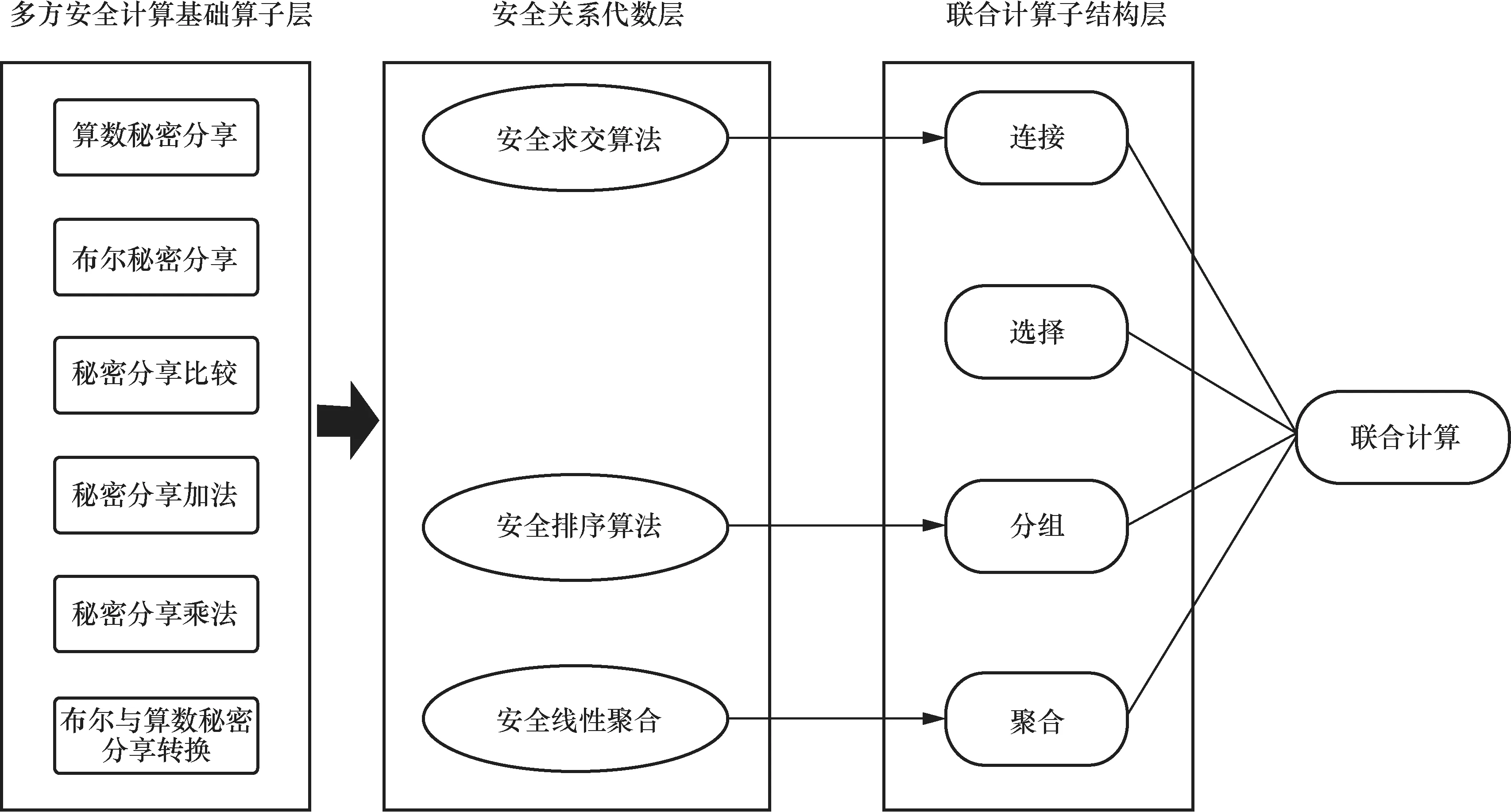
图2 MPC 核心组件3 层结构示意图

2.2 安全关系代数层

2.2.1 安全求交算法

本文应用的安全求交算法结合了基于椭圆曲线的非对称加密算法和秘密分享算法。基于椭圆曲线的非对称加密算法于1986年被提出，该算法与RSA算法相比能用更短的密钥长度实现相同的安全性。在基于椭圆曲线的非对称加密算法中，假设A方生成的公钥与私钥分别为PA和SA，B方生成的公钥与私钥分别为PB和SB，双方共用基点G，则PA=SA*G且PB=SB*G。因此可以推断出明文通过A方公钥加密B方私钥签名，与通过B方公钥加密A方私钥签名，得到的加密结果相同，这个性质也被用于安全求交算法中。此外，本文应用的安全求交算法中还使用了布尔秘密分享算法，保障了求交算法的安全性。

在本文的安全求交算法中，A方和B方生成各自的公私钥对，并使用本方公钥对本方数据进行加密后发送给对方；参与方对接收到的对方发送的加密数据进行置换处理，从而混淆数据位置，并使用私钥对置换后数据进行签名；A方将签名后的数据发送至B方，B方对两方所有经公钥加密、置换处理、私钥签名的数据进行集合求交计算（由基于椭圆曲线的非对称加密算法的性质可知，原始数据相同则经上述步骤加密的数据也相同），得到密态数据对应的A方有效向量和B方有效向量（若A方第i个加密数据出现在交集中，则A方有效向量第i位为1，否则为0）。B方将B方有效向量发送至A方，A方对B方有效向量进行逆置换处理恢复原数据位置，B方则对A方有效向量进行逆置换处理恢复原数据位置，双方将有效向量的布尔秘密分享给对方，双方的求交结果均以布尔秘密分享态形式分散在双方。

针对安全求交算法笔者进行了进一步优化：并行化安全求交算法中的公钥加密和私钥签名步骤。在安全求交算法中，公钥加密和私钥签名这两个步骤需要用到大量的幂运算，为CPU密集型任务。由于不同数据的加密、签名操作相互独立，因此可以采用并行化计算，从而可以使用计算机的多核同时进行加密、签名的幂运算，充分利用计算机多核处理器，减少运算时间。使用上述并行化优化，将其与未经优化的安全求交算法对比，算法运行效率实验结果如图3所示。从图3可以看出，基本模型对220条数据进行求交操作，耗时为272.66 s，优化模型对220条数据进行求交操作，耗时为40.73 s，优化效果明显。

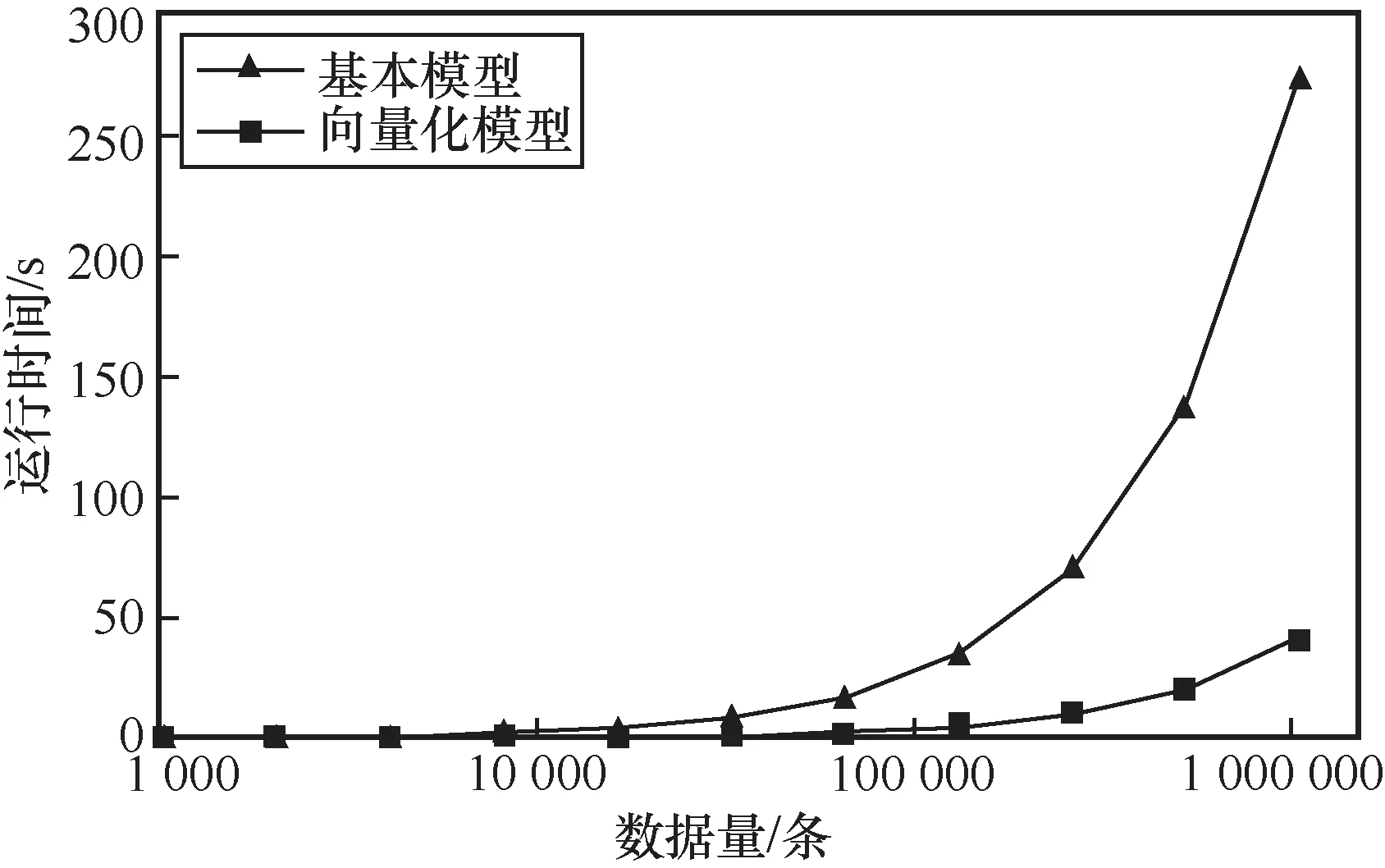
图3 基本模型与经优化的安全求交算法运行效率对比

2.2.2 安全排序算法

本文使用不经意基数排序算法作为安全排序算法。Hamada K[23]于2014年提出了不经意基数排序算法，该算法结合了基数排序算法和不经意传输算法，能在不暴露元素比较关系的同时保证排序的正确性；且该算法无须使用安全比较协议，因此效率较高，适用于数据量较大的场景。

在本文的安全排序算法中，对于以布尔秘密分享态的形式分散在A方和B方的序列，按照低位优先的顺序，获取序列中每个元素对应位置的单比特数据，将该单比特的布尔分享态数据转化为算术秘密分享态数据；根据算术秘密分享态数据中0和1的数量，利用秘密分享的乘法和加法算子计算算术秘密分享态的新顺序；在经过不经意扰乱之后，将新顺序恢复为明文；各个参与方将序列根据恢复为明文的新顺序进行重排序；循环上述步骤，直至完成对序列所有有效位的遍历。

针对安全排序算法笔者进行了进一步优化：在不经意基数排序算法中，需要将布尔秘密分享态的序列的每一个比特转化为算术秘密分享态，若序列中元素的最大位数为k，则需进行k轮转化操作，一共需要k轮通信。因此将序列中每个元素的k个比特横向展开为长度为k的01向量，将每个元素对应的01向量纵向组合为01矩阵，对该矩阵进行转化操作，使用1轮通信即可完成全部转化。另需要在后续的不经意扰乱和重排序步骤中对该矩阵进行置换排序。使用上述优化方法减少通信轮次，与未经优化的安全排序算法对比，算法运行效率实验结果如图4所示。从图4中可以看出，未经优化的安全排序算法运行时间随数据量增加而显著增加，对212条数据进行排序，耗时为3 113.01 s；优化后的算法运行时间随数据量增加而缓慢增加，对212条数据进行排序，耗时为1.65 s，对220条数据排序，耗时为166.38 s，对数据量较大的场景有较好的适用性。

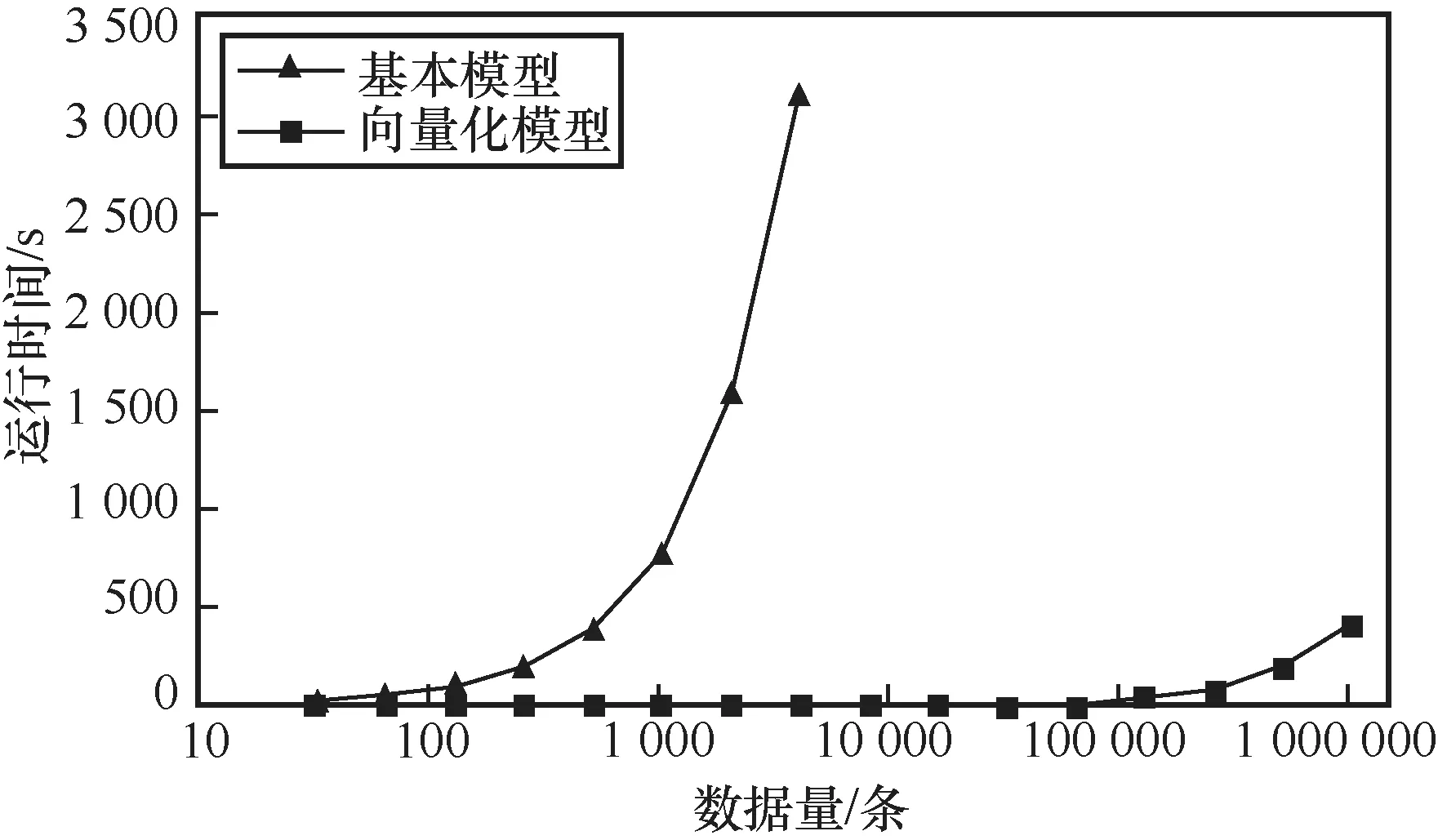
图4 基本模型与经优化的不经意基数排序算法运行效率对比

2.2.3 安全线性聚合算法

本文的安全聚合算法采用线性聚合的方式。对于由算术秘密分享态键值对(keyi,valuei)组成的序列，其中key已是有序状态，需要根据key的不同，对value进行分组聚合。安全线性聚合算法将同一个分组内value的聚合结果存放在该分组的最后一个位置，相同分组内的其他位置填充为0，同时产生一个算术秘密分享态的有效向量来标记聚合结果序列中的有效值（valuei为聚合结果，则有效向量第i位为1，否则为0）。

在安全线性聚合算法中：首先按照顺序扫描由键值对(keyi, valuei)组成的序列，每次选取相邻位置的键值对，即(keyi,valuei)和(keyi+1, valuei+1)；若keyi和keyi+1相等，则将valuei更新为0，且将valuei+1更新为聚合valuei和valuei+1的结果；若keyi和keyi+1不相等，则不进行操作；直到完成对整个序列的遍历。

针对安全线性聚合算法笔者进行了进一步的优化：将序列分割成多个小数据块，进行分批聚合处理，在批次内可以通过向量化，单次运算完成多个聚合操作。当批选取的数量为2时，算法退化为原始的安全线性聚合算法。安全线性聚合过程中采用的是线性扫描，参与方之间需要进行频繁通信，导致该算法效率较低。而采用批处理安全线性聚合算法可以提高通信单轮所能完成的聚合数量，减少通信轮次。使用批处理安全线性聚合算法，与未经优化的安全线性聚合算法对比，算法运行效率实验结果如图5所示。从图5中可以看出：未经优化的算法对216条数据进行安全线性聚合操作，耗时为49 574.51 s。经优化的算法对216条数据进行安全线性聚合操作，耗时为1 801.81 s；对220条数据进行安全线性聚合操作，耗时为28 897.52 s。

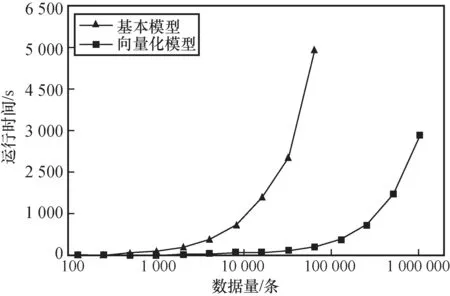
图5 基本模型与经优化的安全线性聚合算法运行效率对比

2.3 联合计算子结构层

2.3.1 连接算法

针对联合计算中的连接运算，本文解决的是无重复值的等值内连接，主要通过安全关系代数层的安全求交算法实现，并用安全排序算法进行辅助。由第2.2.1节可知安全求交算法的输出是分布在A方和B方的求交有效向量的布尔秘密分享态结果。在完成安全求交后，双方的数据仍然是乱序的，因此需要将A方和B方具有相同ID的数据进行对齐。本文采取的数据对齐方式为：在A方与B方分别将布尔秘密分享态的有效向量与ID、ID对应的其他属性进行绑定，依据有效向量和ID进行不经意基数排序。经过排序后，不在交集内的数据行会出现在表的上半部分，在交集内的数据行会出现在表的下半部分。最后将交集内数据的布尔秘密分享态ID、A方秘密分享态属性、B方秘密分享态属性进行连接，得到秘密分享态的对齐数据。

针对连接算法笔者进行了优化。在联合计算场景中，ID为各参与方所持有，因此可以在ID的持有方在明文下按照明文ID进行排序后，再根据有效向量进行排序。在此过程中，明文ID下排序的顺序会被最后一个根据有效向量的不经意基数排序打乱顺序，参与方无法根据最后的顺序推测出原始的明文ID信息和交集的具体数据信息。

2.3.2 选择算法

联合计算中的选择运算分为只有一个选择条件和存在多重选择条件两种情况。对于选择算法中只有一个选择条件的情况，直接使用秘密分享的比较算法，即可得到秘密分享的比较结果。对于选择算法中存在多重条件判断的情况，则可能出现与、或、非3种逻辑运算，可以使用算术秘密分享的加法和乘法进行构造。选择算法的数据安全保护策略是：使用基于秘密分享的比较和通过算术秘密分享的加法和乘法实现逻辑运算，最终的输出为秘密分享态的有效向量。

针对选择算法笔者进行了优化。针对每一个条件，若输入属性的属主为同一参与方，则可以在明文下进行计算，否则必须进行多方安全计算。当所有的单条件完成计算后需要进行多条件融合，若相邻单条件的属主为同一参与方，同样可以在明文下进行计算。对于条件中输入属性的属主为同一参与方的情况，可以通过谓词下推的优化方式，将该条件移动为连接算法的前置步骤，从而减少连接算法的输入数据量，进一步提高运行效率。

2.3.3 分组算法

针对联合计算中的分组算法，需要依据KEY=(key1, key2,..., keyk)对秘密分享态的表进行排序，主要通过安全关系代数层的安全排序算法实现。通过排序算法，具有相同KEY的数据会被排列在相邻位置。对于根据多个key进行分组的情况，根据基数排序的性质，本文采用最低位优先（least significant digit first，LSD）的方法，按照从右至左遍历KEY，即keyk,..., key2,key1的顺序，每次不经意基数排序即可。

笔者对分组算法进行了优化。在联合计算场景下，单个keyi被单一参与方所持有。因此在进行排序时，可以将keyi在数据的持有方恢复为明文，在明文下完成排序。由于有效向量不属于任何参与方，因此在分组算法的最后，必须根据秘密分享态的有效向量使用不经意基数排序算法完成排序。由此可见，通过将部分不经意基数排序转化为明文下的排序，减少了多方安全操作的数据量，提高了算法运行效率。

2.3.4 聚合算法

针对联合计算中的聚合算法，在完成分组算法之后，根据分组和待聚合的属性，使用安全关系代数层的安全线性聚合算法，即可完成聚合操作。在安全线性聚合算法完成后，各个分组的聚合结果存放在相同分组的最后一行。

笔者对聚合算法进行了优化。依据KEY=(key1, key2,..., keyk)对数据进行了分组，需要在分组的基础上进行聚合操作。在聚合算法中对KEY的比较为等值比较，等值比较顺序符合交换律。因此可以根据keyi的属主交换顺序，将具有相同属主的keyi交换放置在连续位置。交换位置后，可以将在相同属主侧的keyi恢复为明文，在明文下完成相邻行的比较。各参与方完成明文比较后再将比较结果用基于多方安全计算的与运算进行合并。用这样的方法可以避免密文下的比较，最多只需进行密文下的逻辑与运算即可，从而降低加密运算量，提升运行效率。

3 基于多方安全计算的公共数据融合创新模式的应用

3.1 公共数据融合创新模式的通用流程

本节以部门A和部门B为例，分析基于多方安全计算的公共数据融合创新模式的通用流程。在公共数据融合创新模式中，部门A拥有与企业相关的数据，包括企业基本信息、企业财务数据、企业信用信息等数据，部门B则拥有企业电力数据，包括企业的年平均用电等级、年用电增长率等数据。部门A希望利用部门B的数据更全面地计算中小企业的经营情况，然而部门B不愿意将数据直接暴露给部门A，因此可以应用基于多方安全计算的公共数据融合创新模式，在双方数据都不出域的前提下，部门A与部门B联合计算中小企业经营情况。对应图1中的基于多方安全计算的公共数据融合创新模式的总体架构，数据提供方为部门A和部门B，结果使用方为部门A，任务调度管理方为公共数据主管部门。

在进行联合计算前需要执行前置步骤：首先，部门A在线申请部门B的数据，通过审批后，公共数据主管部门部署多方安全计算核心组件，多方安全计算核心组件是整个联合计算过程的关键；其次，部门A和部门B分别部署多方安全计算节点，作为计算资源受多方安全计算核心组件统一调配，用于加密的交互计算过程；最后，打通各方的网络，使公共数据主管部门能顺利分发联合计算任务给各计算节点，部门A与部门B之间能顺利地完成加密样本对齐过程和加密交互计算过程。

在完成前置步骤后可以进入联合计算环节：首先由部门A向公共数据主管部门发起利用部门B的数据计算中小企业经营情况的联合计算任务，公共数据主管部门收到任务后，对该联合计算任务进行合规性审核，通过审核后将任务分发给部门A和部门B部署的计算节点。其次，多方安全计算核心组件控制所有计算资源，对部门A本地公共数据和部门B本地公共数据进行加密样本对齐，在完成样本对齐后通过多方安全计算核心组件进行加密交互计算，得到最终的联合计算结果。联合计算过程中，公共数据主管部门对部门A和部门B部署的计算节点进行监督，防止某方通过恶意攻击获取对方隐私数据等违规行为的发生。最后，部门A获得联合计算得到的更全面的中小企业经营情况，并利用该计算结果进行后续工作。该实例具体流程如图6所示。

3.2 公共数据融合创新模式的应用实例

公共数据的使用已经贯穿于政府管理各个环节之中，用数据决策、用数据管理、用数据监督已成为常态，多方安全计算技术可以为公共数据的融合创新提供有效的解决方案。公共数据主管部门需优先开发利用与民生紧密相关、社会迫切需要、行业增值潜力显著的公共数据，重点推进普惠金融、医疗保险、交通出行、公共卫生、环境保护等行业应用。目前，浙江省已经完成第一批高频共享数据的“一数一源一标准”治理，建成数据元标准库和标准字典库，并利用多方安全计算技术在保护隐私数据的前提下实现公共数据的共享开放流通。浙江省积极推动标准数据回流，赋能基层治理，有效支撑温州市“海上综合智治”、湖州市“数字健康”、嘉兴市南湖区“企明星”应用、台州市黄岩区模具产业大脑等数字化改革应用。如嘉兴南湖区融合省平台回流的企业年报基本信息等36类数据、市平台回流的市级高新技术研发中心认定信息等7类数据，构建企业政策专题库，支撑“企明星”政策治理集成应用，解决政策资源和企业需求的错配、信息不对称等问题，优化提升营商环境。

如图7所示，浙江省税务局、浙江银保监局、浙江省电力公司等利用一体化智能化公共数据平台的多方安全计算服务，采用“数据不出域、可用不可见”的方式，共享纳税、企业用电、代发工资等敏感数据，在确保个人数据和信息安全前提下，支撑“共同富裕企业精准画像”“中小企业经营现状分析”“稳就业和参保扩面”等应用实例。目前3个场景的运行计算已全部完成。在浙江省税务局共享税务登记、非正常用户、注销以及纳规标准达标等纳税信息，浙江省统计局进行共同富裕企业精准画像的实例中，554万全量数据任务已计算完成，达到纳规标准146 715件，达标率2.65%；在浙江省电力公司提供企业用电数据，浙江银保监局进行中小企业经营现状分析的实例中，利用电力数据对78 000余家企业进行评分匹配，得到8 000余条优质企业名单信息；在浙江银保监局提供企业代发工资信息，浙江省人力社保厅进行稳就业和参保扩面的实例中，从2 700万目标人员中获得代发工资人员约55万名。

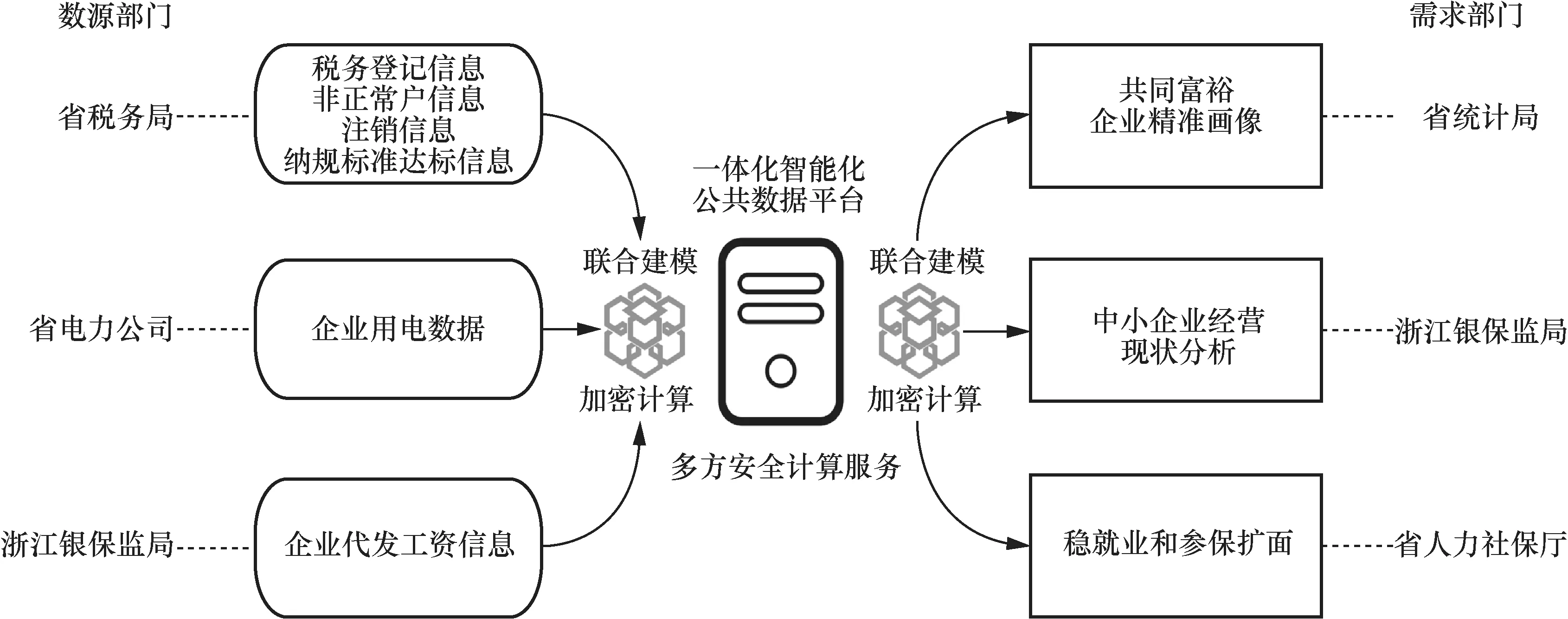
图7 省税务局、浙江银保监局、省电力公司等利用多方安全计算技术共享敏感数据

4 总结与展望

本文基于多方安全计算技术，构建了一套系统完备的公共数据融合创新模式，旨在提升公共数据的利用率，拓展价值实现的新途径。基于多方安全计算的公共数据融合创新模式能在数据不出域的前提下充分释放数据的价值，但是在未来基于多方安全计算的公共数据融合创新模式的实际部署和运作过程中必然会面临新的挑战和问题。由于多方安全计算技术专业性较高、难度较大，对公共数据主管部门来说是一个挑战。同时还可能面临另一种挑战，那就是在公共数据融合创新模式中，不可避免地存在统筹规划、协调推进的管理难度。但是，挑战是值得的，而且很有意义。