喷砂除锈并联机构抗非匹配干扰自适应反步滑模控制

张文杰，高国琴

（江苏大学 电气信息工程学院，江苏 镇江 212013）

0 引言

近年来，路桥基建事业的高速发展，使得钢箱梁在我国桥梁建设行业的应用越来越广泛［1］。喷砂除锈是钢箱梁表面处理中最常用的前处理工艺，钢箱梁表面喷砂除锈的效果决定了后期桥梁主体表面涂料附着力及桥梁路面铺装的耐久性［2］。然而，由于钢箱梁为超大型构件，目前国外采用的喷砂机器人结构较为复杂，且需要构建大型厂房进行固定安装，无法满足钢箱梁随桥梁建设进行流动施工的要求。而国内喷砂除锈仍采用人工操作，存在生产方式落后，以及需要操作人员在危险工况下进行高强度工作，导致危害身体健康等问题［3］。为此，本文设计研制一种基于Stewart 并联机构的喷砂除锈机器人，可以提高钢箱梁喷砂除锈作业效率，并保证其表面具有符合工程验收要求的微米级粗糙度［4］。

喷砂时通过压缩空气将喷料高速喷射到需处理的工件表面，因此在喷砂机构工作时喷枪喷嘴处会产生较大的射流反作用力［5］。这种反作用力直接作用在喷砂除锈并联机构动平台端，表现在机构的运行上就是带来额外的加速度，使得机构在极短时间内发生位姿偏转，造成机构位姿速度的突然变化，从而对并联机构系统造成了强烈干扰。该干扰会造成喷砂机构末端负载的增加，且随着末端位姿变化，影响喷砂机构运动时的动态性能，降低并联机构末端控制的稳定性和轨迹跟踪精度。为此，本文拟研究如何抵抗射流反作用力对系统运行的影响，以增强并联机构系统的鲁棒性，实现其轨迹跟踪控制的高精度。

1 相关研究

喷砂射流反作用力作用于并联机构系统位姿速度通道，从控制角度看是一种非匹配干扰。在并联机构运行过程中，喷枪末端由于高速喷射砂石所产生的强大射流反作用力将直接作用于并联机构，且会随喷枪角度的变化而变化，从而影响系统运行时的安全性及控制精度。由于射流反作用力直接影响喷砂除锈并联机构末端位姿速度，且与控制输入不在同一通道，因此针对射流反作用力非匹配干扰问题的研究仍具有挑战性，特别是针对移动式喷砂机器人存在的射流反作用力非匹配干扰，目前还未有相关研究。

滑模控制始于20 世纪50 年代，是一种特殊的非线性控制，其滑模面的设计需满足李雅普诺夫稳定性要求，即要求参数摄动和干扰是可以通过控制量消除的。因此，传统的滑模控制只能处理非线性系统匹配干扰问题，而对于不在控制输入通道中的非匹配干扰，传统的滑模控制则不能起到良好的控制效果。针对喷砂除锈并联机构喷枪末端射流反作用力的强烈干扰，难以保证Stewart 型六自由度并联机器人运行稳定性的问题，文献［6］提出一种结合射流反作用力前馈补偿的反步自适应滑模控制方法，定量分析喷砂射流反作用力并进行前馈补偿，以降低滑模控制设计负担，提高滑模控制的适应性，但需要首先对射流反作用作复杂的幅值计算。国内外很多学者不断尝试将滑模控制应用于工业机器人控制中，以解决其中的非匹配干扰问题，取得了很多成果。文献［7］采用线性矩阵不等式的积分滑模控制方法解决离散线性系统的非匹配干扰问题，采用积分滑模的方法由于需要设计较大的切换增益，会加剧滑模控制抖振，而引入饱和函数在削弱抖振的同时也增加了控制器设计负担；文献［8］针对柔性关节机器人的非匹配干扰控制问题，采用变权高斯径向基函数对非匹配不确定性进行补偿，提出一种基于反步控制的自适应滑模控制方法，但利用高斯核函数作函数逼近需要大量输入样本，且会增大权值矩阵；文献［9］提出一种求解非匹配干扰系统的滑模控制方法，采用多滑模面（MSS）方法结合惯性延迟控制（IDC）估计非匹配干扰。该方法将滑模控制器设计成系统的相对降阶，且需要设计多层滑模面，增加了控制器的设计负担。

基于扰动观测器（DOB）的鲁棒控制策略能有效解决不确定系统控制问题，是一种处理系统非匹配干扰问题的常用方法。文献［10］针对存在非匹配不确定性的系统，提出一种基于非线性扰动观测器的滑模控制方法，通过设计一种基于扰动估计值的新型滑模面来消除非匹配干扰；文献［11］针对存在匹配和非匹配干扰的非线性系统，提出一种基于扰动观测器的连续有限时间滑模控制方法，保证了滑模面的有限时间可达性以及控制输出的有限时间收敛性；文献［12］提出一种基于干扰观测器的反步轨迹跟踪控制方法，估计系统中的未知复合干扰，降低了反步递推过程的复杂程度。以上文献利用扰动观测器来解决非匹配干扰问题，要求非匹配干扰有界且一阶导数在稳态时趋于零，同时干扰估计误差上界已知。对于本文所研究的喷砂并联机器人，其系统的不确定性受实际工作环境影响，所受射流反作用力无法直接测量得到，因此只能采用观测器进行估计。传统干扰观测器要求扰动一阶导数近似为零，但在实际操作中，射流反作用力不能满足此要求。而采用扩张状态观测器（Extended State Observer，ESO）可将上述条件放宽，只需非匹配干扰有界，且能够在已知系统少量模型信息情况下对非匹配干扰进行估计和补偿，不需要满足射流反作用力干扰一阶导数近似为零的条件。因此，本课题拟引入扩张状态观测器处理喷砂除锈并联机构的射流反作用力非匹配干扰问题。

文献［13］在20 世纪80 年代末首次提出自抗扰控制（ADRC）的概念，扩张状态观测器是自抗扰控制的重要组成部分，扩张状态观测器的提出受到了传统状态观测器的启发，不同的是该方法将系统的总扰动扩张为系统状态，从而使扩张状态观测器可同时估计系统的不确定性和所扩张的未知状态；文献［14］提出一种适用于非匹配不确定性非积分链系统的广义扩张状态观测器（ESO）方法，扰动补偿增益后，非匹配不确定性可以从系统输出中衰减；文献［15］针对一类存在不确定性的系统，提出一种扩张状态观测器对系统的不确定性进行估计；文献［16］提出的基于非线性扩张状态观测器的自适应反步滑模控制方法，能够保证估计误差收敛到原点附近的小邻域内，从而有效抑制非匹配扰动对系统跟踪的影响；文献［17］设计了一种ESO来观测和补偿机器人系统中存在的外部干扰和参数不确定性，并结合自适应滑模控制（SMC）策略实现了机器人的轨迹跟踪控制；文献［18］针对针对电压源逆变器系统中的负载扰动和参数摄动，提出一种基于时变增益扩张状态观测器的自适应超螺旋鲁棒电压控制新方法。但目前将扩张状态观测器应用到并联机构非匹配不确定性问题的研究较少，特别是对于喷砂除锈并联机构存在的特殊的射流反作用力问题尚无相关研究。

反步设计法是将系统状态作为中间控制变量进行逐步设计，在逐步递推过程中设计中间虚拟控制量，以对并联机构系统的非匹配干扰进行补偿。从前面分析可知，滑模控制对匹配扰动具有鲁棒性，但是对非匹配干扰不能起到良好的控制效果，而反步控制可以处理非匹配干扰，但无法保证鲁棒性。因此，可将滑模控制与反步设计方法相结合来设计控制器，以解决具有非匹配干扰的控制问题。基于对以上研究的分析，扩张状态观测器可以对系统状态和不确定扰动进行在线估计，可将反步设计法和滑模控制器相结合以抑制系统扰动，增强系统的鲁棒性。因此，本文考虑采用扩张状态观测器对射流反作用力非匹配干扰进行实时估计，通过反步法设计含自适应切换增益的滑模控制器，解决传统滑模控制因系统不确定性上界未知而引起的增益过估计问题，并提高系统的收敛速度。最后进行样机实验并设计基于Simulink 的系统仿真实验，以验证所提出的结合扩张状态观测器的并联机构抗非匹配干扰自适应反步滑模控制方法的有效性，并总结研究结论。

2 系统描述

2.1 喷砂除锈并联机构介绍

图1 是本文自主研制的一种用于喷砂除锈的并联机器人，其由1-末端喷枪、2-并联机构、3-喷砂软管、4-移动平台、5-升降机构、6-电气控制柜、7-上位机组成，包括移动平台、升降机构和并联操作机构3 个功能部分。由移动平台承载升降机构和并联操作机构，实现在地面移动及转向定位功能；升降机构位于移动平台上，通过并联操作机构定平台与并联操作机构垂直联接，携并联操作机构实现升降运动；并联操作机构的动平台中心固定联接喷枪夹持机构，该喷枪夹持机构可随并联操作机构实现六自由度运动，可实现上下升降、前后左右自由移动以及六自由度位姿的精准运动操作，且具有高承载力、高精度和能实现微米级喷砂的优点。

Fig.1 Prototype of sandblasting and rust removal parallel robot图1 喷砂除锈并联机构样机

六自由度并联机构由动静平台、6 个电动缸以及12 个虎克铰组成。在静平台中心Og建立惯性坐标系OgXgYgZg，在动平台中心Od建立运动坐标系OdXdYdZd，分别设动静平台上的虎克铰坐标为Ai、Bi(i=1，…，6)。动静平台之间由虎克铰与电动缸连接［19］，通过电动缸的伸缩运动，动平台可以进行六自由度的空间运动：沿运动坐标系X、Y、Z轴移动，分别用变量x、y、z表示；绕X、Y、Z轴转动，分别用欧拉角α、β、γ表示。位于动平台上的动平台夹持电机转动角度为θ，如图2所示。

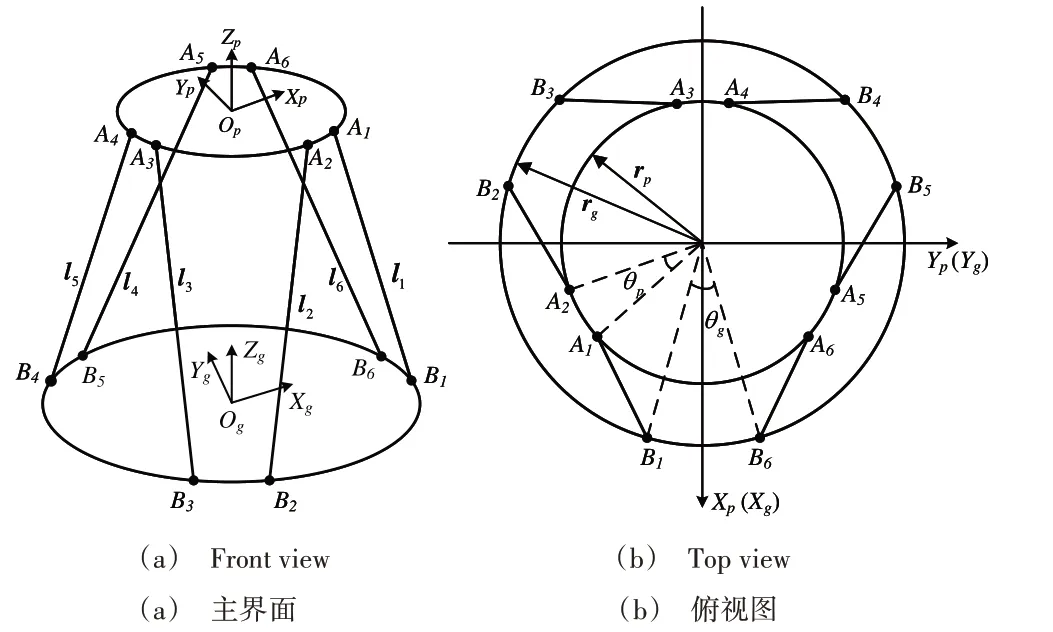
Fig.2 Sand blasting and rust removal Stewart parallel mechanism diagram图2 喷砂除锈Stewart并联机构简图

2.2 研究问题阐述

从喷砂除锈作业机理分析，喷砂时通过压缩空气将喷料高速喷射到需处理的工件表面，由于磨料颗粒喷出时速度很快，会对钢箱梁表面产生冲击和切削力，将其表面铁锈清除来达到标准的粗糙度要求，以改善工件表面的机械性能，提高工件的抗疲劳性［20］。根据动量守恒定律，喷砂时必然会产生较大的射流反作用力，这种反作用力直接作用在喷砂除锈并联机构的动平台端，会给系统的运行带来不良影响，具体为在机构的运行上带来额外的加速度，使机构在极短的时间内发生位姿偏转。因此，可将其视为一种作用于位姿速度通道上的非匹配干扰。

喷砂除锈并联机构运行时存在射流反作用力非匹配干扰，想要通过滑模控制保证系统的鲁棒性，必须解决滑模控制过程中存在的抖振问题。本文结合了喷砂除锈并联机构实际工作情况建立考虑了射流反作用力非匹配干扰的Stewart 并联机构动力学模型，研究设计一种反步滑模控制算法，以抑制干扰中超出观测器带宽的快速时变项和其他误差项［21］，进一步提升系统的鲁棒性，同时提高其跟踪性能，并在此基础上设计自适应律动态调整滑模控制切换增益，从而达到抑制滑模控制抖振的效果。

2.3 具有射流反作用力的六自由度并联机构动力学模型

拉格朗日法是从能量角度出发，将系统内部所有约束力视为理想约束力，可省略机构系统内部约束力的推导过程。因此，通过拉格朗日法对并联机构进行动力学分析。拉格朗日函数T定义为系统动能T与势能P之差，即L=T-P。根据拉格朗日方程：

式中，q为末端位姿向量，Q为并联机构末端位姿q在笛卡尔空间下的广义力/力矩。

根据机构关节空间与笛卡尔空间之间的转换关系，建立在关节空间下包含并联机构不确定因素的动力学方程。转换关系如下：

式中，J为并联操作机构雅可比矩阵，τ为各主动关节驱动力矩，即6 个电动缸的输出力矩。进一步得到六自由度并联操作机构的工作空间动力学方程：

式中，M(q)为惯性矩阵，为哥氏力和离心力项，G(q)为重力项，为末端加速度项的矩阵方程。

考虑到机构在工作过程中存在的其他随机干扰和建模误差等，推广可得六自由度并联操作机构关节空间下的动力学模型为：

然后在此基础上引入射流反作用力在位姿速度通道上所引起的干扰项，并整理成状态空间方程的形式如下：

式中，d2=M-1(-D(t)-ΔM-ΔC-ΔG)为并联机构动力学集总干扰，可以看出d2与广义力控制量Q处于同一通道，是匹配干扰，而d1与广义力处于不同通道，属于非匹配干扰。将上述状态空间方程写成如下形式：

式中，f(x1，x2)=M-1(G-Cx2)，b=M-1。

3 控制器设计及稳定性分析

本文研究具有射流反作用力的六自由度并联机构抗干扰控制问题，基于扩张状态观测器的反步自适应滑模控制原理如图3 所示。图中，代表喷砂除锈并联机器人末端位姿与速度，代表扩张状态观测器对在干扰状况下的末端位姿与速度的观测值代表射流反作用力的扩张状态变量。以控制系统的跟踪误差e和作为自适应反步滑模控制器的输入，采用反步法进行控制器设计，在该过程中引入扰动观测值进行补偿，在反步控制最后引入滑模面s，构成反步滑模控制器。同时，对全局鲁棒滑模控制切换增益η设计一种自适应律，从而构建自适应反步滑模控制器。最后把实际获得的主动关节位姿x和速度通过运动学正解转换为末端的运动位姿q与速度，并反馈给扩张状态观测器，从而实现闭环控制［22］。

Fig.3 Controller principle block diagram图3 控制器原理框图

3.1 扩张状态观测器设计

设立含射流反作用力非匹配干扰的非测量辅助变量，将含非匹配不确定性的混联机构动力学方程重构为仅含匹配不确定性的状态方程。

根据式（7），可将式（6）所示的状态方程重构为：

其中，h(t)为有界的不确定函数。

式中，li(i=1，2，3)为正数。

则由式（11）可得：

当li＞0(i=1，2，3) 时，可以使det|λI-A|满足Hurwitz 多项式，即A为Hurwitz 矩阵。因此，存在一个实对称正定矩阵P和正定矩阵Q，使得ATP+PA=-Q，存在ε＞0，使得成立。

3.2 反步滑模控制器设计及稳定性分析

基于扩张状态观测器对射流反作用力的观测结果进行控制器设计，并证明位移跟踪误差、滑模函数和观测器误差一致最终有界。在以下推导过程中，k1＞0，c1＞0 为控制器参数。

步骤1：定义e1=z1-z1d为位移跟踪误差，其中z1d为位移指令信号。对e1求导得：

定义Lyapunov 函数：

对式（14）求导得：

定义e2=z2+z3-z2d，其中z2d为虚拟控制变量。为保证负定，令得：

由式（15）、式（16）得：

定义切换函数：

结合式（13）可得：

由于k1＞0，c1＞0，显然，如果S=0，则e1=0，e2=0且。因此，需要进行下一步设计。

步骤2：定义第二层的Lyapunov 函数。

对式（19）求导，根据式（16）和式（18）可得：

设计基于扩张状态观测器的反步滑模控制律为：

式中，δ为滑模增益，且δ，h均为正常数，将式（22）代入式（21）中可得：

控制器稳定性证明如下：

针对所设计的李雅普诺夫函数，取：

结合位移跟踪误差，进一步可得：

通过调整参数h，c1和k1的值，可使得|U|＞0，从而保证U为正定矩阵［23］。

在保证U为正定矩阵的情况下，则有：

因此，闭环系统满足Lyapunov 稳定条件，滑模变量可在有限时间内收敛到平衡点。

3.3 Lyapunov自适应律设计

在控制律（22）的基础上，采用自适应技术动态调整滑模控制切换增益，所设计的自适应律［24-25］为：

式中，λ为自适应调整参数，且λ＞0。

结合反步滑模函数，定义Lyapunov 函数如下：

结合式（29）设计反步自适应滑模控制器为：

将式（25）和式（29）代入式（28），可得：

在保证U为正定矩阵的情况下，有。因此，在控制律（30）和自适应律（27）下，闭环系统是渐近稳定的，轨迹跟踪误差能收敛于零。

4 仿真实验及结果分析

为了验证本文所提出的反步滑模控制方法对解决射流反作用力非匹配干扰的有效性，采用MATLAB/Simulink进行仿真分析。仿真时考虑并联机构的建模误差以及外部随机扰动等不确定因素的影响，并联机构建模误差为标称模型的10%。

根据表1 中的仿真参数进行仿真，得到分别采用3 种滑模控制器时的末端轨迹跟踪曲线，如图4所示。

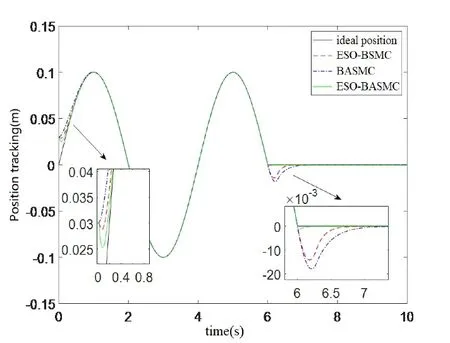
Fig.4 End trajectory tracking curves of different sliding mode controllers图4 不同滑模控制器末端轨迹跟踪曲线

另外，仿真时分两步进行对比实验：首先用具有扩张状态观测器但无自适应的反步滑模控制方法（ESOBSMC）与自适应反步滑模控制器（BA-SMC）作对比。滑模控制只有提高切换增益值才能克服建模误差以及不确定性问题，但是切换增益选取过高势必引起大的滑模控制抖振。从仿真图5 和图6 的对比可看出，反步自适应滑模控制中各主动关节输出力矩抖振明显较大，而考虑了扩张状态观测器对射流反作用力的实时估计并加以补偿后，各主动关节输出力矩的抖振明显减小。

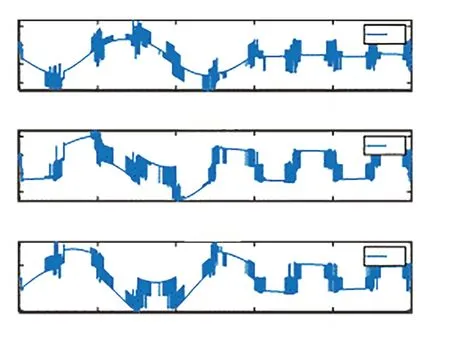
Fig.5 BASMC output torque of active joint图5 BASMC主动关节输出力矩

Fig.6 ESO-BSMC output torque of active joint图6 ESO-BSMC 主动关节输出力矩

然后在上步考虑了扩张状态观测器但无自适应的反步滑模控制器中引入本文设计的Lyapunov 自适应律，得到最终的结合扩张状态观测器的自适应反步滑模控制关节输出力矩。通过仿真图6 和图7 可以看出，本文设计的Lyapunov 自适应律可进一步抑制各主动关节输出力矩抖振。

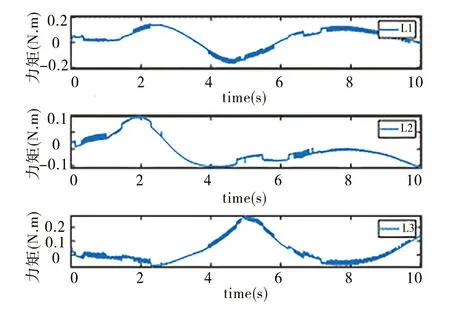
Fig.7 ESO-BASMC output torque of active joint图7 ESO-BASMC主动关节输出力矩

5 样机实验

根据喷砂除锈并联机构样机，搭建抗非匹配干扰的自适应反步滑模控制实验平台进行并联操作机构运动控制实验，设置一种喷砂射流反作用力实验模拟装置。该装置由手摇绞盘、数字式推拉力计及弹力带构成，如图8 所示。数字式推拉力计一端连接手摇绞盘，另一端通过弹力带连接到喷枪尾部，从而实时显示射流反作用力模拟装置在机构运行中反作用力的数值变化，通过人为地收放绞盘缆绳模拟射流反作用力的剧烈变化（见图9）。

Fig.8 Jet reaction force simulation device图8 射流反作用力模拟装置

Fig.9 Instructions of jet reaction force simulation device图9 射流反作用力模拟装置使用方式

通过样机实验得到六自由度并联机构各个时刻的运动状态，读取其各支腿驱动电机的期望位置与实际位置，然后基于正运动学分析迭代公式，换算出末端动平台的期望位姿与实际位姿。给出间隔0.5 s 采样点时刻对应的末端动平台期望位姿与实际位姿，如表2所示。

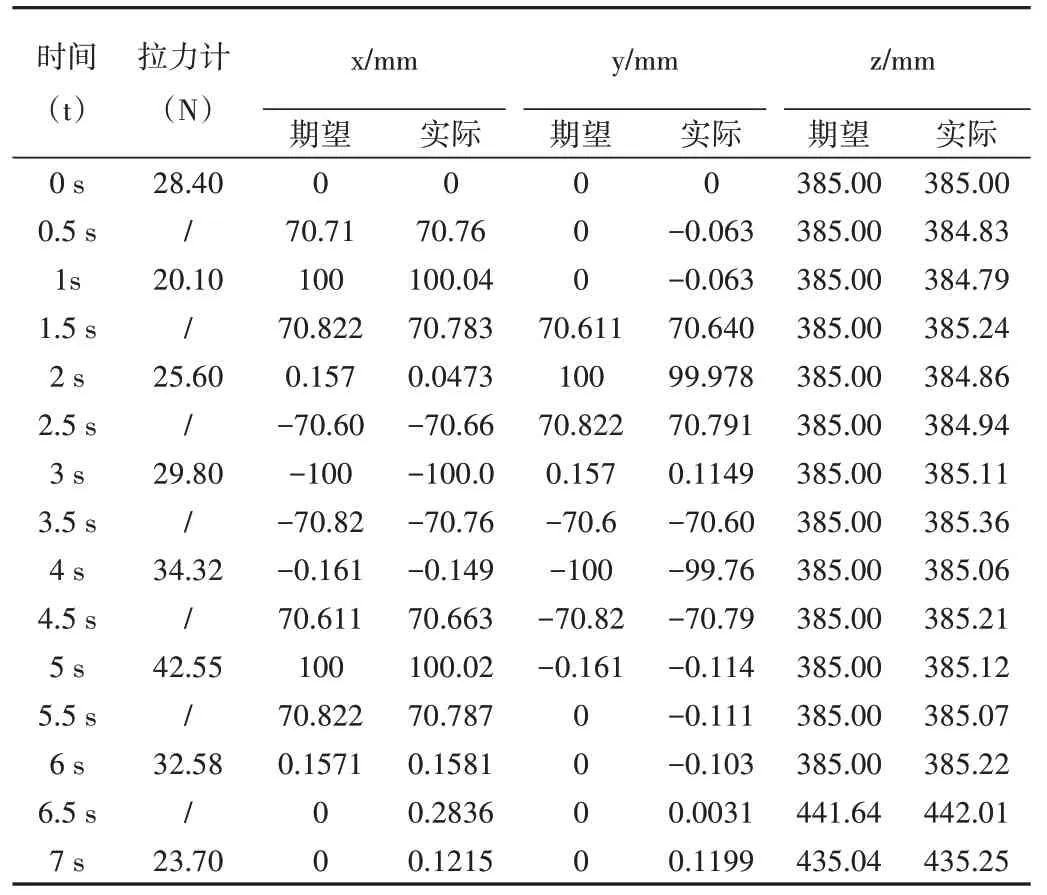
Table 2 Components of the expected pose and actual pose of the end moving platform表2 末端动平台期望位姿与实际位姿各分量

表2 中列出了在实验过程中不同时刻拉力计的数值以及动平台在各个分量上的位姿。由数据可以得出，在X轴方向的最大位移跟踪误差绝对值为0.23 mm，均方根误差为0.104 mm；在Y轴方向的最大位移跟踪误差绝对值为0.956 mm，均方根误差为0.185 mm；在Z轴方向的最大位移跟踪误差绝对值为0.21 mm，均方根误差为0.155 mm。实验结果验证了所提出方法的有效性，在没有采用抗射流反作用力非匹配干扰控制器的情况下，当射流反作用力模拟装置输出的干扰力达到一定程度，会引起机构末端喷枪夹持电机的跟踪精度降低，以致超出伺服电机的安全运行阈值，伺服驱动器自动锁死电机以进行保护。而加载了本文所设计的抗非匹配干扰反步自适应滑模控制算法后，喷砂除锈并联机构运行较为稳定，验证了抗射流反作用力非匹配干扰的必要性。

通过CK3M 配套的Power PMAC IDE 集成开发软件读取电机位置误差实验数据，得到支腿主动关节跟踪误差，如图10所示。

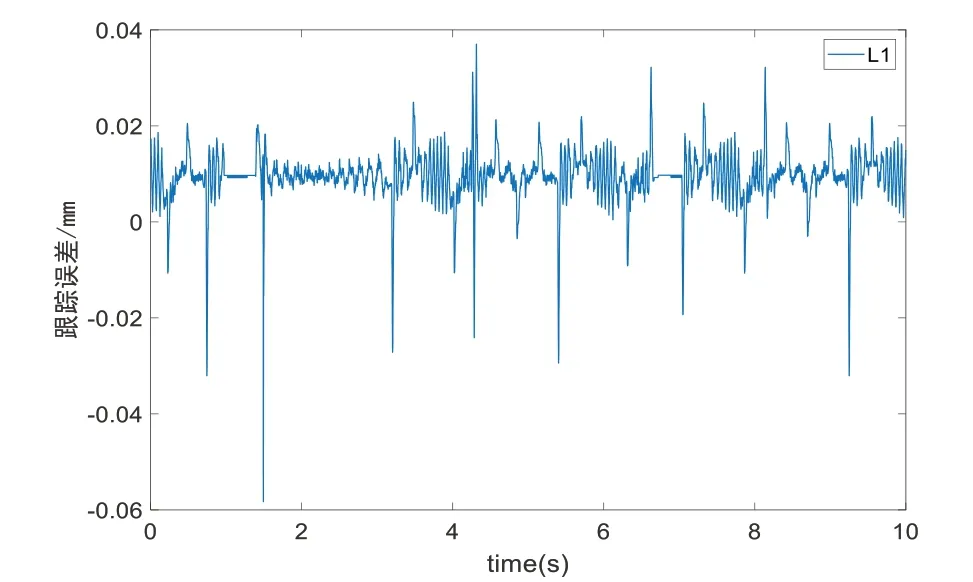
Fig.10 Active joint displacement tracking error of leg图10 支腿动关节位移跟踪误差

上述实验结果表明，本文所提出的结合扩张状态观测器的喷砂除锈并联机构抗非匹配干扰反步自适应滑模控制方法具有良好的轨迹跟踪精度，验证了该方法对射流反作用力非匹配干扰的有效性。

6 结语

针对喷砂除锈并联机构中射流反作用力的非匹配干扰问题，提出一种基于扩张状态观测器的反步滑模控制方法，对其稳定性进行了理论分析，得到滑模函数和观测器误差一致最终有界。对联合仿真结果及误差数据进行分析，通过扩张状态观测器对射流反作用力引起的干扰估计结果可得，在受到强扰动时，基于扩张状态观测器的反步滑模控制方法可以对射流反作用力非匹配干扰进行有效估计。

针对控制系统中存在的建模误差及系统外部的随机干扰问题，设计的反步自适应滑模控制器可有效增强系统的鲁棒性，并抑制滑模控制抖振。

在喷砂除锈并联机构受到射流反作用力强烈干扰时，与传统反步滑模控制器和无扩张状态观测器的自适应反步滑模控制方法相比，本文提出的基于扩张状态观测器的反步滑模控制方法位移跟踪精度高，并能有效抑制复合扰动，鲁棒性强。