基于多层Voronoi图索引的非点型空间对象区域查询方法研究

明 梓，刘 伟，李 旸，崔俊杰，刘 刚，李佳惠，雷梦婷

（1.湖北工业大学 经济与管理学院，湖北 武汉 430068；2.长江信达软件技术（武汉）有限责任公司，湖北 武汉 430014；3.中国地质大学（武汉）地理与信息工程学院；4.中国地质大学（武汉）计算机学院，湖北 武汉 430078；5.湖北工业大学 计算机学院，湖北 武汉 430068）

0 引言

城市化进程的加快带来了交通拥堵、空间环境恶劣等问题，给我国智慧城市的建设带来了挑战［1-4］。合理开发与利用城市地理空间大数据，借助物联网和人工智能等技术对城市地理空间资源进行智能管控与高效调度是解决上述问题的有效途径。在面向城市地理空间大数据的地理信息系统（Geographic Information System，GIS）建设中，高效的空间查询技术是关键基础［5-9］。其中，区域查询方法是应用最广泛的一类查询方法，可以快速检索到指定区域内包含的全部地理空间对象（例如建筑、植被、公共设施、车辆等），帮助城市管理者了解城市地物的分布情况，从而为其提供决策支持。

基于空间边界约束的查询通常被称为空间区域查询，即从该数据库中检索出一个指定区域内的所有数据对象，这个目标区域可以是任何形状的封闭几何图形。目前主流区域查询算法均基于R-tree 提出，但由于R-tree 在面对大规模、非均匀分布的城市空间大数据时会出现节点重叠、结构失衡等一系列问题，以R-tree 索引为基础的区域查询算法很难有理想表现。因此，MVD（Multi-layer Voronoi Diagrams）索引被提出，其通过多层Voronoi 网络结构替代传统树形结构，有效规避了上述问题［5］。以MVD 为基础的区域查询算法在面对城市空间大数据时展现出更高的查询效率（即查询算法的响应速度），但其无法直接对非点型数据进行索引，因此基于MVD 的区域查询方法不支持非点型空间数据。

针对上述问题，本文基于MVD 索引提出一种针对非点型空间对象的区域查询技术框架：首先通过最小外包圆（Minimum Bounding Circle，MBC）对空间对象进行拟合，实现MVD 索引对非点型空间对象的存储管理；然后根据空间对象最小外包圆的半径上界对查询区域进行边界拓展，实现MVD 索引对非点型空间对象的区域查询，进而提出MVD-Polygon 算法。为进一步优化MVD-Polygon 算法的查询效率，采用空间对象尺度对数据进行分级管理，从而加速查询过程，并将优化后的MVD-Polygon 命名为MVDPolygon-Grade。为验证该方案的有效性，将MVD-Polygon、MVD-Polygon-Grade 与基于R-tree 的主流区域查询算法Multi-step 进行性能比较，结果表明MVD-Polygon 算法拥有更高的查询效率。

1 相关研究

空间区域查询最早由Willard［10］提出，并提供了一种以O(nlog64)复杂度求解的方案，其中n为数据库中的数据总量；而后，Paterson 等［11］基于B-tree 提出一种计算复杂度为O(k·logn+s)的求解方案，其中k为多边形边的数量，s为结果集大小。自R-tree 索引被提出后，绝大多数区域查询方法都开始采用该索引作为基础来实现。为减少PIP（Point in Polygon）验证次数，Kriegel 等［12］基于R-tree 索引提出一种通过两级过滤策略实现的空间区域查询算法Multi-step，该算法通过查询区域的外包近似形从R-tree 中检索出一个候选集，然后对候选集中的对象逐一过滤，筛选出最终结果集。R-tree 内部的基本单元都是空间正交矩形，而正交矩形之间的空间关系运算非常简单快速，因此一般情况下都是利用正交的最小外包矩形（Minimum Bounding Rectangle，MBR）来构建查询区域的近似形。在Oracle Spatial 组建中，区域查询也是基于R-tree 实现的，但其不需要利用空间近似形进行初次过滤，而是直接利用查询范围进行检索［13］。在这种区域查询算法的执行过程中，虽然部分节点与查询区域之间的空间拓扑关系运算成本会有所增加，但总体I/O 成本有效降低。

城市地理空间数据的多中心非均匀分布会加剧Rtree 索引的节点重叠，因此在面向城市地理空间大数据的GIS 系统中，基于R-tree 实现的区域查询算法需要访问大量索引中间层节点，并产生大量冗余空间关系验证，进而导致基于R-tree 的Multi-step 区域查询算法在面对海量对象、空间关系复杂的场景中存在查询效率较低的问题。为进一步提升复杂场景下的算法查询效率，Li等［14］基于复合型索引VoR-tree 提出一种利用Voronoi 图实现的区域查询方法Voronoi-Region，并将该方迁移至高性能的多层网络结构索引MVD 中［5］。借助MVD 的非树形结构，该算法在避免访问大量中间节点的同时削减了绝大部分冗余数据点的访问和验证，有效提升了海量对象以及复杂空间关系场景中针对点型数据的区域查询效率。然而，Voronoi图的构建需要以一个离散点集合为基础，以Voronoi 图为基础部件的MVD 索引仅支持点型数据管理，即相对应的区域查询方法无法适用于非点型数据检索。

为此，本文基于MVD 索引提出针对非点型数据的管理方式和相应的区域查询算法，以解决MVD 索引不支持非点型数据管理以及其对应的区域查询算法无法对非点型数据进行区域查询的问题，进而改进目前主流算法在海量对象与复杂空间关系场景下对非点型数据进行区域查询时效率不足的问题。

2 基于边界扩展的MVD区域查询技术

2.1 总体技术框架设计

基于MVD 索引实现针对非点型空间数据的高性能区域查询方法需要解决两个重点问题：第一是如何实现MVD 索引对非点型空间对象的存储管理？本文基于MVD索引的点对象与非点型空间对象之间的关系构建起两种映射关系，完成对非点型空间对象的管理；第二是如何基于MVD 索引设计针对非点型空间对象的区域查询方法？本文采用引入缓冲区的方法构建候选集，并对候选集中的对象进行空间关系验证，得到最终结果集。同时基于初始查询边界拓展查询边界，实现MVD 索引对非点型空间对象的查询，并基于空间对象尺度的数据分级方法加速查询过程。总体技术框架见图1（彩图扫OSID 码可见，下同）。

Fig.1 Overall technical framework图1 总体技术框架

2.2 非点型空间对象存储管理方法

针对非点型空间对象的管理方式需注意两个方面：①MVD 索引结构是以点对象为基础构建的，非点型空间对象需基于MVD 索引结构进行管理；②MVD 索引结构管理非点型空间对象时需完整地存储非点型对象数据。

针对第一个方面，MVD 索引结构以点对象为基础构建，需要选择某个点来代替非点型空间对象构建索引结构。本文选择非点型空间对象的质心代替整个对象构建MVD 索引结构，构建质心与整个对象一对一的映射关系。非点型空间对象与质点映射关系如图2所示。

Fig.2 Mapping relationship between non-point spatial object and centroid图2 非点型空间对象与质心映射关系

针对第二个方面，非点型空间对象包含众多数据，如对象的边界线数据、尺度数据、属性数据等。在完成这些数据的存储后，本文根据质心与这些数据的关联关系构建一对多的映射关系。

以上两种映射关系可以通过非点型空间对象的质心ID 进行关联。其中，第一种映射关系通过非点型空间对象的质心构建MVD 索引，然后通过针对点对象的空间查询方法进行区域查询，可以得到非点型空间对象的质心构成的点集；第二种映射关系根据点集中的点对象ID 与其对应的非点型空间对象ID 的映射关系即可查询到整个非点型空间对象的全部数据。

2.3 基于边界扩展技术的MVD索引区域查询方法

基于边界扩展技术的区域查询方法总体流程如图3所示。该方法主要包含两个核心技术，分别为基于MBC半径的查询区域边界扩展方法和基于扩展边界的候选集验证方法。基于MBC 半径的查询区域边界扩展方法的主要思路为通过引入缓冲区来增大区域查询范围，使候选集包含所有查询结果；基于扩展边界的候选集验证方法的主要思路为通过对候选集中的对象进行空间关系验证来筛选出最终结果集。

Fig.3 Overall process of region query method based on boundary extension technology图3 基于边界扩展技术的区域查询方法总体流程

2.3.1 基于MBC半径的查询区域边界扩展方法

选择非点型空间对象的质心构建MVD 索引后，如果仅直接按照将质点视为整个非点型空间对象的思路进行区域查询，则会造成质点在查询区域外，但其实际对应的非点型空间对象在查询区域内的情况，本文将其称为漏检问题。针对该问题，本文在原有区域查询边界的基础上引入缓冲区来构建候选集。为表述方便，定义以下概念：①空间对象尺度，指空间对象最小外包圆的半径值，用R 表示，点对象的尺度为零；②缓冲区尺度，指构建缓冲区过程中在查询边界外侧所作的平行线与查询边界的垂直距离，用L表示；③数据集尺度，数据集中全体空间对象尺度的最大值代表该数据集的尺度，即Rmax=Max{R1，R2，R3，…，Rn}，用Rmax表示。

以缓冲区边界为基础执行对点对象的区域查询方法，得到由质心构成的点集，点集中的质心所对应的非点型空间对象构建成了候选集。只要缓冲区边界可以包含所有结果，便可以避免漏检现象。因此，在初始区域查询边界的基础上引入何种尺度的缓冲区是关键问题［15-17］，基于极限思想，当缓冲区尺度大于或等于数据集中最大尺度的非点型空间对象时，缓冲区边界恰好包含所有结果。以图4为例，尺度最大的非点型空间对象为4 号，其质心为p点，尺度为Rmɑx，如果仅看区域查询边界，p点在区域查询边界之外，当缓冲区尺度L等于Rmɑx时，缓冲区边界可以包含所有区域查询的结果（p点在缓冲区边界内），这些结果构成了针对非点型空间对象的区域查询算法的候选集。

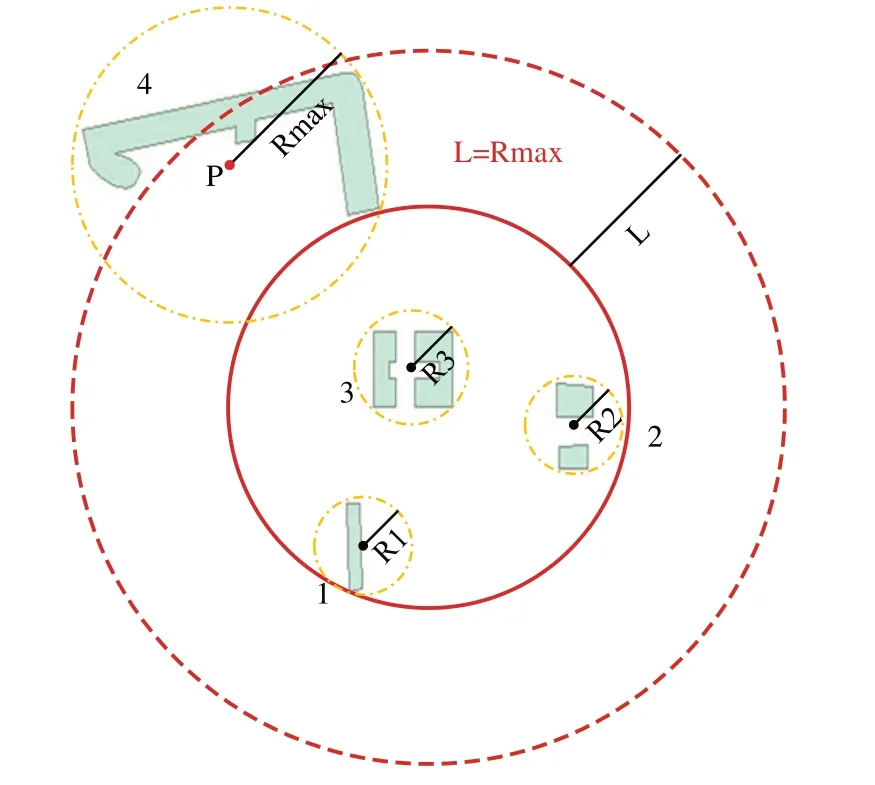
Fig.4 Schematic diagram of maximum value of buffer scale图4 缓冲区尺度极大值示意图

综上可知，基于初始查询边界引入合适尺度的缓冲区便可使所有结果包含在缓冲区范围内。对于区域查询边界，分别在其外侧作距边界线一定距离的平行线可生成缓冲区边界［18］。根据查询区域原始边界的顶点坐标和缓冲区尺度可以求得每个原始顶点到其在缓冲区边界上对应顶点间的向量d，从而得到缓冲区边界上所有顶点的坐标。每个顶点对应的向量d的计算步骤如下：

（1）构建单位向量。如图5 所示，对于当前区域查询边界上的点p来说，其与左右相邻点n、m构成两个向量，设向量为n，向量为m，其单位向量分别为a和b。

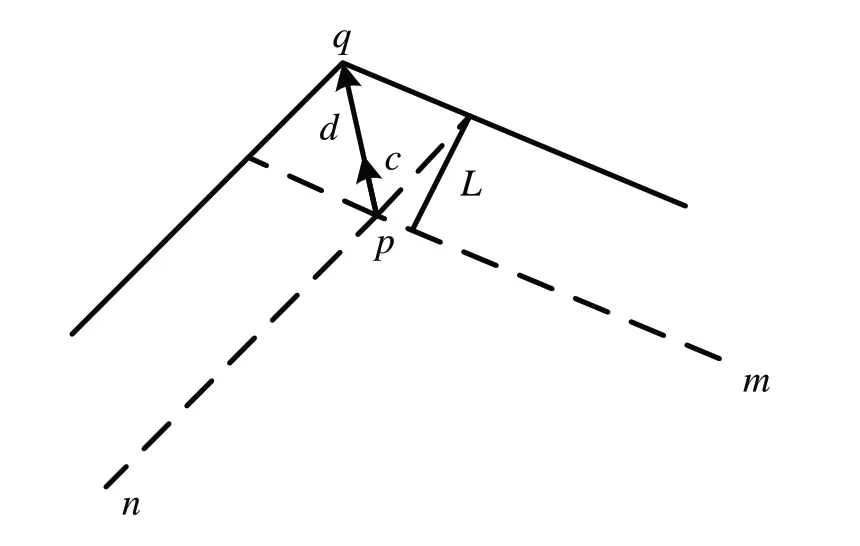
Fig.5 Schematic diagram of buffer intersectionc图5 缓冲区交点示意图

（2）计算扩大后的向量。计算出单位向量后，由于两个方向的向量大小模长均为1，将a和b向量相加并取反得到外扩方向上的单位向量c。

（3）计算缓冲区边界上的交点。缓冲区尺度为L，取向量c的反向向量-c与m的角度，进而计算向量-c与向量m的距离dis。计算dis与L的比值，根据比值计算向量c方向上的目标向量d，计算方法见式（1）。最后根据两个向量求出目标点q。

基于数据集尺度引入对应尺度的缓冲区，然后利用缓冲区边界对空间对象集对应的质心点集执行范围查询，即可得到充分包含所有结果集对象的候选集。具体步骤为：①获取区域查询范围边界；②基于原始区域查询边界引入数据集对应的缓冲区，得到缓冲区边界；③基于缓冲区边界进行针对点数据的区域查询，得到质心集合；④基于“2.2”节中的第一种映射关系即可通过质心集合中的质心ID 查询到质心对应的非点型空间对象，这些非点型空间对象构成了候选集。

2.3.2 基于扩展边界的候选集验证方法

当候选集构建完成后，需要对其中的对象进行过滤，以得到最终结果集，其中过滤主要是验证结果集中非点型空间对象与区域查询边界之间空间关系的过程。候选集中的非点型空间对象可分为两类：第一类是质心在区域查询边界内的对象，第二类是质心在区域查询边界与缓冲区边界之间的对象。如图6 所示，1、2、3 号对象为第一类对象；红点处为第二类对象。

Fig.6 Schematic diagram of two types of non-point spatial objects图6 两种非点型空间对象示意图

针对第一类对象进行空间关系验证，如果某个空间对象的质心在区域查询边界内，说明这个对象一定与查询边界存在相交或包含关系，属于区域查询的结果集，只需要进行一次针对点对象的区域查询即可得到由质心构成的点集，点集中的点所对应的非点型空间对象即为构成结果集的对象。

针对第二类对象进行空间关系验证，只需要判断是否至少满足以下两个条件之一：①该空间对象至少存在一个边界顶点在查询区域内部（避免边的重合）；②该空间对象的边界与查询区域边界相交。本文采用引射线法判断二者是否相交［19-20］，如果存在相交关系，则将其纳入结果集中。

2.3.3 算法步骤

基于MVD 索引的针对非点型空间对象的区域查询算法步骤为：

2.4 基于空间对象尺度分级的索引构建策略

由上文可知，基于初始查询边界引入合适尺度的缓冲区便可将所有结果包含在缓冲区范围内。如果数据集中的非点型空间对象尺度相近，引入缓冲区进行区域查询后候选集中只包含少量冗余对象。然而在城市空间查询场景中，数据集中的非点型空间对象尺度不一定相近，例如一个城市的人工湖、大型商场、一个电话亭的尺度完全不在一个数量级，根据城市内最大尺度对象的尺度引入缓冲区后，区域查询的候选集中会包含大量冗余对象。如果根据尺度对数据集中的对象进行分类，手动将尺度相近的对象分在同一个数据集中，例如将电话亭、汽车等尺度在米级别的对象分到一个数据集中，将商场、学校等百米级别的对象分到另一个数据集中，以此构成若干个子数据集，并分别引入对应尺度的缓冲区进行查询，则可有效减少候选集中的冗余对象。

如图7 所示，以澳门市建筑轮廓的一部分为研究对象构建各尺度子数据集的候选集，建筑对象构成了数据集，将数据集内的对象手动分为大、中、小尺寸的3 个子数据集，并分别引入相应尺度的缓冲区。其中，图7（a）为数据集未进行尺度划分的情况，引入整个数据集中尺度最大的空间对象的尺度（图中5 号对象的尺度）作为缓冲区边界，质心在缓冲区内的所有非点型空间对象均被纳入到候选集中，共包含20 个对象，其中1、2、3、4 号对象为区域查询的最终结果。图7（b）、（c）、（d）为3 个不同尺度的子数据集引入对应尺度缓冲区后的结果。子候选集中的对象个数分别为6、2、0，对子候选集取并集构成最终候选集，共包含8 个对象，且1、2、3、4 号对象均包含其中。可以看出，对数据集进行分级预处理可有效减少候选集中的冗余对象。

Fig.7 Schematic diagram of candidate subset construction of sub data sets of all scales图7 各尺度子数据集候选集构建示意图

3 实验方法与结果分析

为验证本文提出的针对非点型空间对象的区域查询算法MVD-Polygon-Grade（以下简称MPG 算法）的性能，以及基于空间对象尺度的数据分级管理方案的查询效率，以基于R-tree 的Multi-step 算法（以下简称MS 算法）和MVD-Polygon（以下简称MP 算法）算法为对照进行评估实验。本实验旨在比较3 种算法的时间效率，即算法完成一次查询所需要的时间，所需时间越少，算法效率越高。为减少误差，实验结果经过50次运行后取算数平均值得到。

3.1 实验环境配置

实验环境主要包括软件和硬件两个方面，详细配置如表1所示。

3.2 数据集

基于尺度相近的对象放到同一个子数据集的原则，本研究根据澳门市12 482 个建筑轮廓的面数据将城市建筑分为5类，构建5个子数据集。具体信息见表2。

Table 2 Information of sub datasets at different scales表2 不同尺度子数据集信息

3.3 结果分析

如图8 所示，澳门市建筑轮廓数据集包含12 482 个建筑轮廓的面数据，这些面数据共由225 807 个边界点构成，平均每个面数据由18 个点表示，符合非点型空间对象的特征。

Fig.8 Outline of buildings in Macao图8 澳门市建筑轮廓

为研究区域查询边界的规则程度对算法效率的影响，分别构建顶点为4～6 个和20～30 个的多边形作为区域查询边界，两组多边形分别构建50 个。为减少查询面积对实验结果的影响，本组实验保证查询区域边界的最小外包圆面积相同，查询面积依次为3 km2、5 km2、8 km2、12 km2、16 km2。由图9 可以看出，无论区域查询边界是否规则，在相同查询面积下，MPG 算法比MS算法和MP 算法具有更高的效率，但MPG 算法比MS 算法更易受到区域查询边界规则程度的影响，区域查询边界越复杂，MPG 算法效率下降得越快。这是由于在MPG 算法的结果集构建过程中，第一类空间对象是基于高效MVD 针对点数据的区域查询算法而来，本身就属于结果集，只需要很低的时间成本即可完成第一类空间对象的确定；而判断第二类空间对象是否属于结果集需要依次对其进行空间关系验证，相对耗时，且区域查询边界越复杂，空间关系验证所需时间成本越高；区域查询面积越小，第二类空间对象占整个候选集的比例越大。基于以上原因，MPG 算法基于空间对象尺度对数据进行分级管理，以确保第二类空间对象很少。MP 算法没有基于空间对象尺度对数据进行分级管理，导致有大量第二类空间对象需要进行空间关系验证，因此与MS 算法相比，MP 算法在区域查询面积较小时并未体现出明显优势。随着区域查询面积的增大，第二类空间对象占候选集对象的比例逐渐降低，MP 算法效率逐渐接近MPG 算法。

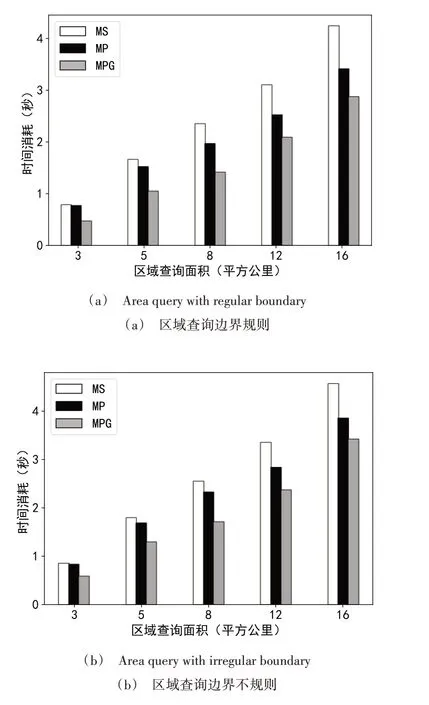
Fig.9 The influence of the rule degree of region query boundary on the efficiency of region query图9 区域查询边界规则程度对区域查询效率的影响

为验证查询区域面积对算法效率的影响，本组实验的区域查询边界形状设置为正交矩形，查询位置随机，查询区域面积分别为3 km2、5 km2、8 km2、12 km2、16 km2，分别占整个数据分布区域的6.2%、10.4%、16.7%、25%、33.3%，每种面积下的查询次数均为50 次，取算数平均值作为最终结果。由图10 可以看出，无论何种查询面积，MPG 算法均比MS 算法和MP 算法有更高的查询效率。在区域查询面积较小的情况下，MP 算法和MS 算法的效率并未表现出显著差异；在区域查询面积较大的情况下，MP 算法的效率接近于MPG 算法，强于MS算法。

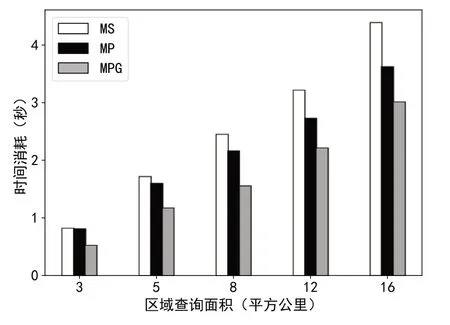
Fig.10 The influence of query area on the efficiency of region query图10 查询区域面积对区域查询效率的影响

4 结语

为合理开发与利用城市地理空间大数据，本文针对MVD 索引只能管理点型数据而无法直接针对非点型数据进行区域查询的问题，设计提出了一种基于边界扩展技术的区域查询算法实现框架。该框架通过最小外包圆对空间对象进行拟合，基于MVD 索引实现非点型空间对象的区域查询，并基于空间对象尺度对数据进行分级管理以提高查询效率。利用澳门市城市建筑轮廓数据进行验证实验，结果表明，在相同查询面积、查询边界复杂程度条件下，本文提出的MVD-Polygon-Grade 算法比Multistep 算法和MVD-Polygon 算法查询效率更高，且数据规模越大、查询面积越大，数据尺度分级层次越明显，MVDPolygon-Grade 算法的区域查询效率越高。本研究提出了从点对象拓展到非点型空间对象的通用数据管理思路和区域查询方法，为进一步挖掘现有索引结构的数据管理潜力提供了支撑。然而该方法仍存在改进空间：①MVDPolygon-Grade 算法的分级方法为前期数据处理过程中的手动粗糙分级，未来将设计针对数据集的最优分级方法，以保证各个子数据集内的数据方差最小，数据集间方差最大，使候选集验证过程中产生最少冗余，进一步提升算法效率；②主要验证了查询面积、查询边界复杂程度对MVD-Polygon-Grade 算法的影响，未来将研究更多因素（如空间对象的密集程度）对该算法的影响，以拓展其应用场景。