基于改进切线角实时算法的滑坡监测预警

贾 丁，陈小红，周永贵

（1.航天宏图信息技术股份有限公司，北京 100089；2.自然资源部地质灾害智能监测与风险预警工程技术创新中心，北京 100081）

0 引言

我国地质灾害频发，滑坡作为我国最主要的地质灾害类型之一，严重威胁人民生命财产安全。我国滑坡数量庞大、分布广泛、发生频率高、突发性强且危害严重，滑坡灾害形势复杂严峻［1-4］。监测预警是主动防范地质灾害的重要手段，滑坡以岩土体变形失控后产生运动的方式造成破坏，变形作为滑坡过程中的显著表征，是滑坡预警的主要依据和关键的监测参数，变形监测是分析滑坡危险程度和演变规律的重要环节［5-6］。全球卫星导航系统（Global Navigation Satellite System，GNSS）作为监测变形和位移的重要方法在滑坡变形监测预警中得以广泛应用［7-10］。

GNSS 的滑坡监测结果主要通过位移—时间数据呈现，对该数据的分析处理是监测预警中的重要流程［11-14］。对于一个完整的滑坡生命周期而言，理想的滑坡监测预警曲线分为初始变形阶段、等速变形阶段和加速变形阶段，如图1（a）所示。切线角指位移—时间曲线各点斜率和时间轴的夹角，是变形速度的体现，位移—时间曲线切线角的变化监测已经成为《崩塌、滑坡、泥石流监测规范DZ/T0221-2006》中推荐方法的重要技术参数。

Fig.1 Ideal landslide displacement-time curve and real complicated situation图1 理想的滑坡位移—时间曲线和实际复杂情况

许强等［15］指出传统切线角定义和计算的不足，提出了改进切线角，并在已有的滑坡应用中进行了检验。王珣等［16］通过建立等速变形速率和临滑切线角的联系，并结合未破坏滑坡变形过程的最大切线角建立了预警判据，得到了较好的应用效果。刘富有等［17］将NGM（1，1，k，c）模型与改进切线角结合对危岩变形趋势进行分析预测。李洋［18］建立了以临界位移量和T-t 曲线切线角“双指标”为阈值进行滑坡预测预报的方法。Tan 等［19］使用切线角计算的思路对微变形雷达监测数据进行处理，并与滑坡预测中的速度和位移双阈值相结合，进行矿区边坡监测预警。

然而，在前人研究中，对切线角计算过程和方法的研究较少。由于计算切线角的求导过程会放大曲线本身的噪声和波动，计算结果往往呈现零散分布状态，且常常有负值出现。同时，改进切线角计算需要在匀速变形阶段对速度进行量纲处理，而匀速变形阶段需要有较长时间的累积以进行趋势判断。但实际情况往往复杂多变，如图1（b）所示，监测曲线中可能遇到多个匀速阶段或者短暂加速及减速阶段，有的匀速速率过大，已经不能用于切线角计算。现有的计算方法中，匀速阶段难以判定，随机性强。上述因素对切线角计算的准确性和时效性均有影响。本文在对位移—时间数据进行移动平均、数据重采样的基础上，采用拉格朗日插值微分法实现了计算结果降噪；同时，提出将变形阶段的含量加以实时统计，以满足切线角计算中匀速阶段的速度更新，提升滑坡监测预警可靠性。

1 改进切线角计算原理

由于环境噪声和各种不确定因素影响，GNSS 得到的原始位移—时间数据具有较大波动性，因此在计算切线角计算前需要进行平滑。本文采用指数移动平均和重采样的方法对数据进行降噪处理。

1.1 指数移动平均

滑坡的GNSS 位移—时间曲线是典型的时间序列。移动平均法在时间序列分析中应用非常广泛［20］，该方法可以对时间序列起到较好的平滑作用，黄智伟［11］验证了该方法在滑坡监测数据中有具有较好的应用效果。本文采用指数移动平均方法对以小时为单位的位移—时间曲线进行移动平滑。

指数移动平均法是对过去所有数据加权平均，权由平滑因子α决定，而且随着时间的推移加权指数递减，故称为指数滑动平均。其公式如式（1）所示。

其中，t为窗口大小，0 ＜α≤1 为平滑因子，α可根据窗口大小计算，如2/(t+1)，也可自定义。(1-α)i为呈指数增加的权重，离预测时刻越近权重越大。图2 为不同大小的平滑窗口得到的平滑结果，可以看出，越大的平滑窗口平滑力度越大，对原始曲线的降噪作用也越好。但过大的平滑窗口也会使曲线丧失一些关键的波动特征，需要适当选取。需要注意的是，指数移动平均结果会损失前面一个平滑窗口数量的数据，在对目标时间段数据进行处理时，需要往前冗余选取一个时间窗口数量的数据。

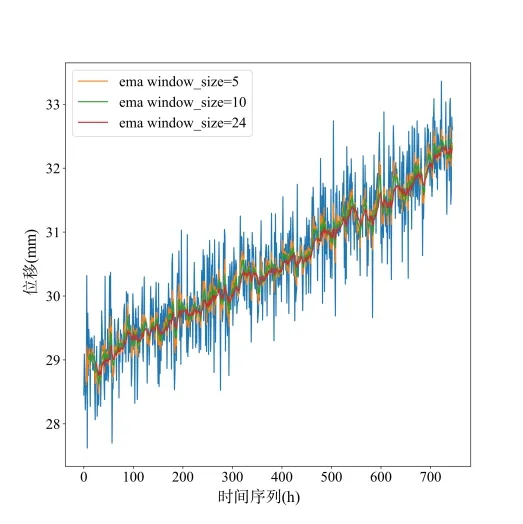
Fig.2 Smoothing effect of exponential moving average on displacement-time curve图2 指数移动平均对位移—时间曲线的平滑效果

1.2 数据重采样

数据重采样是信号处理领域的常用方法。在时间序列中，重采样可以将时间序列从一个频率转化为另一个频率进行处理。将高频率数据转化为低频率数据为降采样，将低频率转化为高频率为升采样。本文采用平均采样方法将每日以小时为单位的数据降采样为以天为单位的位移—时间数据。图3 为重采样前后的结果，重采样可以减少对曲线局部变化的关注，突出曲线整体变化趋势。

Fig.3 Results of data resampling by day图3 按天进行数据重采样结果

1.3 切线角计算

改进切线角反映的是每一变形阶段的变形速度与匀速变形阶段速度的相对大小。切线角的改进可以统一不同时间单位，如周、天、小时下的计算结果。其计算原理为：通过用位移除以匀速变形阶段的速度v的做法将曲线S-t的纵坐标变换为与横坐标相同的时间量纲，即定义如式（2）所示。

其中，ΔS(i)表示某一单位时间段（一般采用一个监测周期，如1 天、1 周等）内的位移变化量；v表示等速变形阶段的位移速率；T(i)表示变换后与时间相同量纲的纵坐标值。这样，T替代S后的曲线称为T-t曲线。根据T-t曲线，可以得到改进的切线角αi的表达式，如式（3）所示。

其中，αi表示改进切线角；ti表示某一监测时刻；Δt表示对应ΔS的单位时间段；ΔT表示单位时间段内T(i)的变化量。显然，根据上述定义有：当αi＜45°时，滑坡处于初始变形阶段；当αi≈45°时，滑坡处于等速变形阶段；当αi＞45°时，滑坡处于加速变形阶段。

2 改进切线角算法优化及动态计算方法

2.1 拉格朗日插值微分算法

上述切线角计算算法中的重要步骤是斜率计算，现有的斜率计算公式如式（4）所示。

通常采用式（4）这种用差分来代替微分的方法，求导本身会放大曲线波动和误差，因此该计算方式得到的切线角结果波动较大。拉格朗日插值微分是一种典型的离散点求导方法，能够同时考虑被计算点左右两侧点的情况，提高计算结果的精度。为了降低切线角计算结果的波动性，采用拉格朗日插值微分五点法中的中心插值微分公式进行计算，如式（5）所示。

在实际应用中，对于被计算数据左侧早期数据点而言，可以选择其左侧数据点进行补充，因而可以始终维持f′(x2)计算方法。如图4 所示，当步长为2 时，计算x2位置点的导数需要用到x0，x1，x3，x44 个点的值。对于右侧点而言，当其右侧没有足够的点维持f′(x2)的计算方法时，经过验证可以通过其与往前2h点的差分作为其求导结果。本文结合前人工作，将式（5）修改为式（6）。

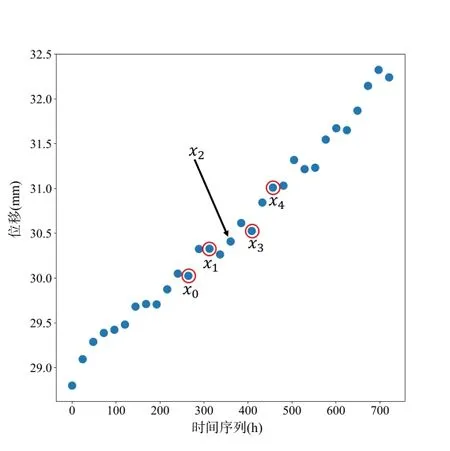
Fig.4 Schematic diagram of Lagrange interpolation differential calculation（h=2）图4 拉格朗日插值微分计算示意图（h=2）

其中，h为拉格朗日插值微分的计算步长，n为数据点总量。

2.2 阶段判识与阶段变形平均速度计算

如上所述，通过变形速度对位移—时间曲线的变形阶段划分为减速变形阶段、匀速变形阶段和加速变形阶段。由于切线角计算要使用匀速阶段速度，因此变形阶段划分判识至关重要。对于较长时间尺度和时间序列的数据而言，曲线的凸凹性可以很好地用来判断曲线速度整体变化趋势。王一帆等［21］提出了通过位移—时间曲线的凸凹性进行滑坡变形阶段判识的方法：定义时间从t1～t3的数据对应的总位移为s1～s3，选取t2为t1～t3时刻的中点，其对应的位移为s2，定义R1=0.5(s3-s1)，R2=s2-s1。定义无量纲参数γ=R2/R1，当0.9 ≤γ≤1.1 时，认为曲线处于匀速变形阶段；当γ＞1.1 时认为曲线处于减速变形阶段；当γ＜0.9 时，认为曲线处于加速变形阶段（见图5［21］）。取t1～t2和t2～t3两段速度平均值作为该阶段的速度，即v=。

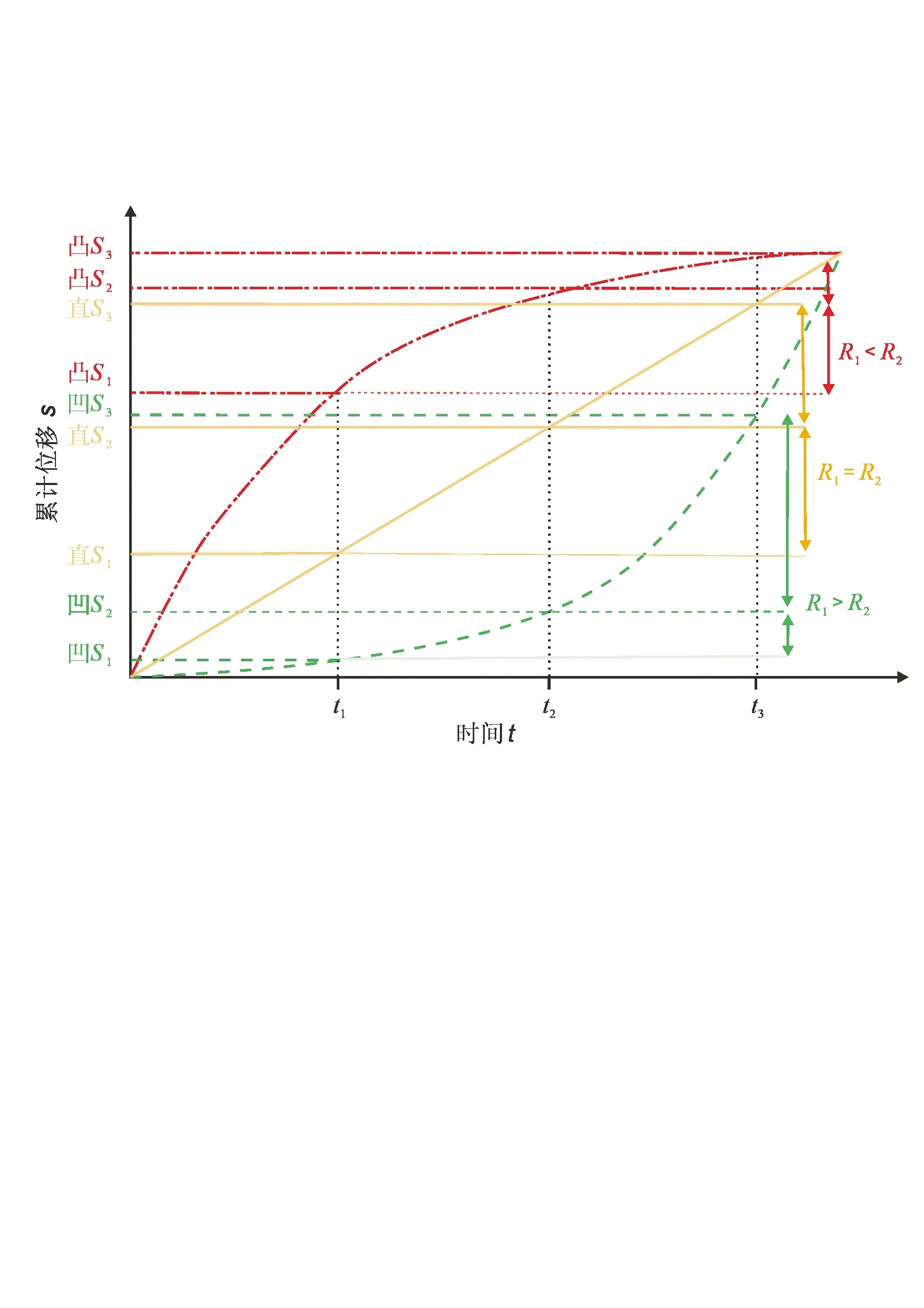
Fig.5 Deformation stage division according to displacement-time curve of convexity and concavity图5 根据凸凹性的位移—时间曲线变形阶段划分

2.3 切线角计算匀速速度更新算法

通常，切线角计算方法中匀速阶段需要长期积累，且计算结果随机性强，对于长期运行、实时监测的监测预警系统而言，其时效性很难达到实用要求。本研究在变形阶段划分基础上，通过一种变形阶段实时统计方法对匀速阶段的选取进行实时判断。

对于某一天ti位移数据，选取其之前m天数据，即ti-m～ti位移—时间数据，通过上述方法可以判定得到该范围位移—时间曲线的变形阶段类型ci。向前统计窗口大小为d，即ci-d～ci的所有阶段类型的含量，记减速、匀速、加速变形阶段的含量为p1、p2、p3，同时计算ci-d～ci每一阶段切线角大小的平均速度。

在上述3 种阶段类型含量和切线角平均值大小的基础上，对用于切线角计算的匀速速率是否更新作为条件进行判断。这种判断可以排除曲线进入加速阶段、减速阶段以及新的匀速阶段变形速率过大等情况。

图6 展示了当m=30、d=30 和d=10 时典型滑坡位移—时间曲线p1、p2、p3的变化趋势。除完全进入加速阶段后加速阶段百分含量p3为1 外，其余时刻由于曲线的波动，3 种变形阶段都会出现。即当曲线整体处于匀速变形阶段时，局部的阶段判识由于曲线波动影响可能会得到减速阶段或者加速阶段的结果。但整体趋势为减速阶段逐渐减少，在进入加速阶段后逐渐上升，进入预警阶段时为加速阶段。

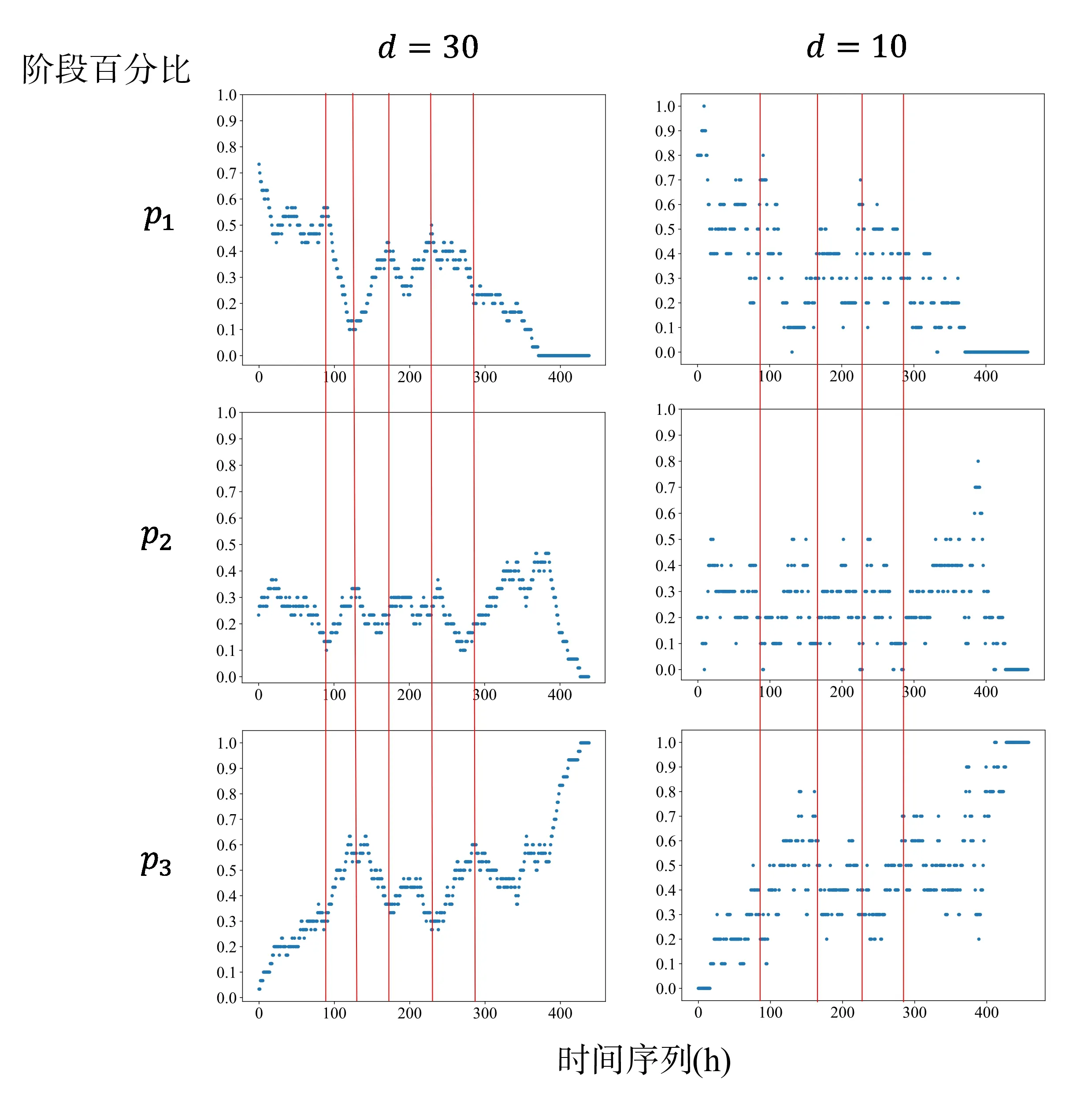
Fig.6 Description of stage content percentage and uniform speed algorithm parameters图6 阶段含量百分比统计和匀速速度算法参数

因此，可以通过限制减速变形阶段百分含量（p1）和加速变形阶段百分含量（p3）的上界、匀速变形阶段百分含量（p2）的下界作为范围条件。同时，为了避免在即将进入加速阶段时匀速速度过大，即如果具有过大的切线角平均值，即使判定为匀速阶段也不对匀速速度进行更新。设置该时段切线角平均值范围大小。当p1、p2、p3和满足上述条件时，对切线角计算所使用的匀速速度进行更新，以此为条件便可以形成匀速速度更新判断方法，在此基础上对时间序列进行迭代即可实现切线角计算结果的动态计算和更新。

在Ubuntu20.04 LTS 系统，Python3.10 环境下完成了优化后的切线角计算和匀速速度更新的算法编程实现。算法如下：

3 实验结果与分析

本文对河南省鹤壁市滑坡灾害监测数据进行实验分析，选取位于灵山地质灾害隐患点的监测数据，时间从2022 年7 月1 日至2023 年6 月30 日。在为期一年的GNSS位移—时间曲线数据中，选取其中一个月的曲线数据进行实验分析，该时间阶段属于滑坡匀速变形阶段。

3.1 计算参数对切线角结果的影响

在拉格朗日插值微分中，步长h插值微分的重要参数对计算结果有很大影响。同时，为了验证指数移动平均法和数据重采样在该算法中所起的作用，采用拉格朗日插值微分方法进行计算，比较不同计算步长h条件下和是否采取数据平滑与重采样的条件下匀速变形阶段的切线角大小。不同计算步长切线角计算结果如图7 所示，移动平均对切线角计算的影响如图8所示。

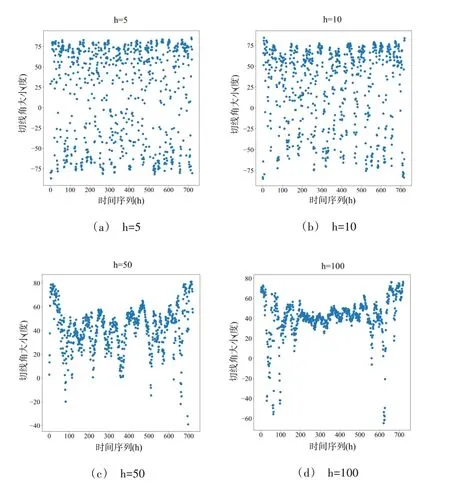
Fig.7 Calculation results of tangent angles with different calculation steps图7 不同计算步长切线角计算结果

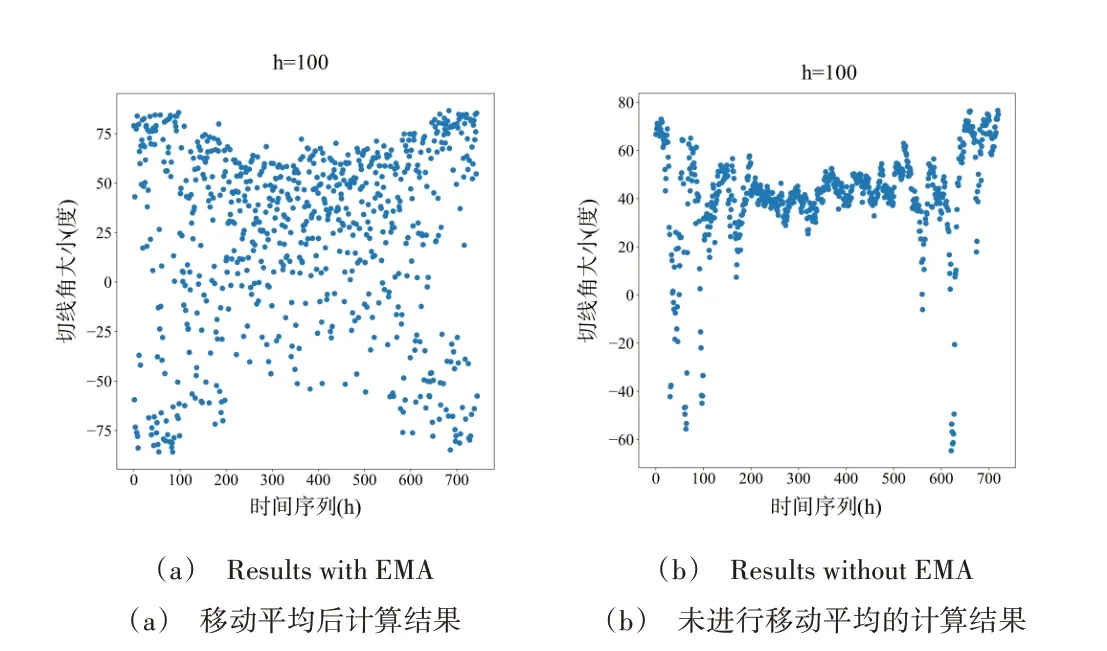
Fig.8 Influence of moving average method on calculation of tangent angle图8 移动平均对切线角计算的影响

重采样前后计算结果比较如图9 所示。以小时为单位时间尺度进行比较，以72 个点的间距为步长进行计算，按每天的平均值进行重采样后，72 小时的步长变为3 天。结果表明，重采样的计算结果能够包含更多数据信息，得到更为精确的结果。

Fig.9 Influence of data resample on calculation of tangent angle图9 数据重采样对切线角计算结果的影响

3.2 拉格朗日插值微分评价

对经过指数移动平均和重采样的数据进行计算比较，图10（a）和图10（b）分别为采用式（4）和式（6）对一段匀速变形阶段的位移—时间曲线的切线角计算结果，步长均设置为5。根据前述切线角计算原理，其理论切线角应为45°左右。式（4）的计算结果波动性大，比较分散，且有负值。而式（6）的计算结果则相对较集中，沿着45°分布。由此可见，该计算方法对切线角计算结果起到了很好的降噪作用，切线角计算结果波动性显著下降。

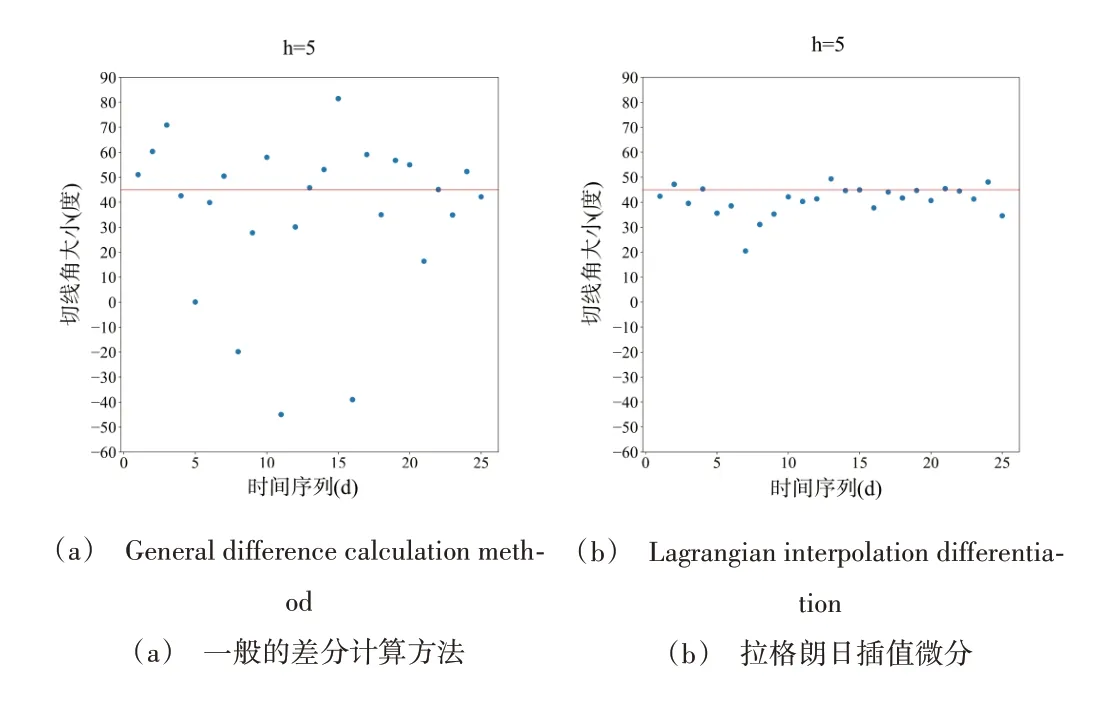
Fig.10 Comparison of calculation results between general difference method and Lagrangian interpolation five-point method图10 差分计算方法和拉格朗日插值五点法求导计算结果比较

为了量化改进后的效果，计算了两组数据相较于匀速阶段应有切线角45°的均方根误差。其计算公式如式（7）所示。

其中，f(xi)为计算值或测量值；yi为真实值，在此处为45°。利用式（7）计算得到算法改进前切线角结果的均方根误差为32.24°，改进后均方根误差为7.31°，精度提高了77.33%。

为了验证该算法在滑坡匀速和加速连续变形阶段的适宜性，在已有一年期的GNSS 位移—时间曲线数据基础上，根据李忠君等［22］提出的非线性蠕变模型，生成了滑坡匀速和加速连续变形的测试数据。依据上述切线角算法，对连续变形阶段进行计算，结果显示在匀速阶段切线角值在45°附近上下波动，进入加速阶段后波动减小并迅速增大至预警值，与实际情况较为吻合，如图11所示。

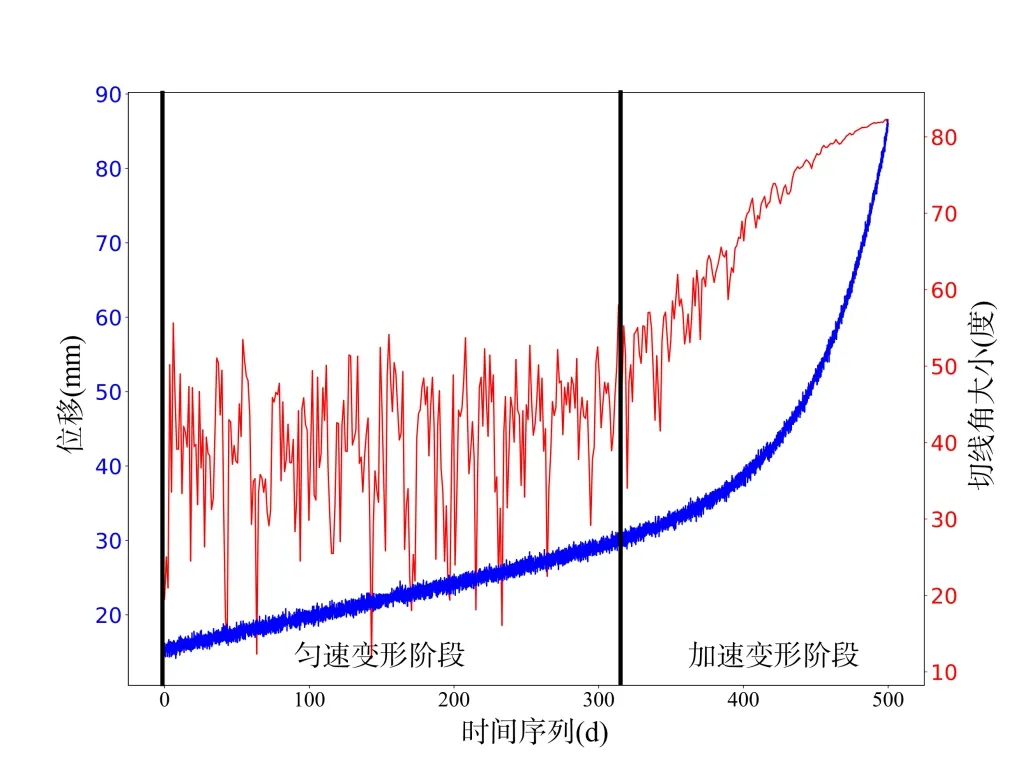
Fig.11 Calculation result of tangent angle of landslide simulation curve图11 滑坡曲线的切线角计算结果

4 结语

改进切线角作为滑坡监测预警中的重要判据指标，在各种监测预警模型中得以广泛应用。本文对改进的切线角计算方法进行了优化研究，采用格朗日插值微分求导算法进行改进切线角的计算，该方法可以尽可能多地利用监测数据，从而提高了计算准确度。实验表明，改进的拉格朗日插值微分算法相对于传统的差分方法计算准确度提高了77.33%。在此基础上分析了计算步长、指数移动平均法、数据重采样对切线角计算结果的影响，最后通过加入阶段判识和用匀速速度更新算法，实现了切线角动态计算。结果表明，指数移动平均法和数据重采样均可以滤除位移—监测曲线数据中的原始噪声，减少计算结果的随机性。通过滑坡阶段判识和阶段含量统计，辅以切线角匀速速度更新的条件判断，实现了切线角动态实时计算，为滑坡监测预警提供实时、动态判据，提高了滑坡监测预警实用性。

改进的算法需在后续滑坡监测预警中针对加速变形阶段进一步加以验证，优化切线角计算中的步长等参数，以适应复杂地质条件的滑坡监测预警。