列车自动驾驶运行高可靠性控制优化方法设计

梁亚成，张宁，虞赛君

（合肥市轨道交通集团有限公司，合肥 230001）

引言

列车自动驾驶运行的研究涉及到多个关键领域，包括列车自动控制、能源管理系统、通信与信号技术、运行调度及列车集群协同等。通过应用先进的控制算法、智能感知技术和通信系统，可以实现列车的自动驾驶、智能调度和交互通讯，从而提高列车的安全性、稳定性和运行效率。尽管自动驾驶运行已经取得了很多进展，但仍需解决多个方面的技术挑战，包括环境感知、定位与地图更新、系统安全性、复杂决策，自动驾驶运行可靠性仍需优化[1,2]。

在列车自动驾驶方面，国内相关专家给出了一些比较好的建议，例如张京等[3]优先构建了列车ATO运行多目标优化方法，将列车过分相区断电惰行纳入控制策略中，改进PSO优化算法，并且将遗传算子融入其中，形成全新的GAPSO算法，对工况转换点展开寻优，最终得到获取自动驾驶运行优化方案。张英贵等[4]将列车最小化发射时刻波动性以及车站轨道运动方案波动性作为优化方法，通过模拟退火算法实现自动驾驶运行优化。盛昭等[5]对列车运行过程展开分解，获取多个主要的关键速度，同时分析列车最小追踪间隔，构建以能耗和运行时间为性能指标的自动驾驶运行优化问题，通过量子进化算法获取最优策略。

随着各项技术不断演进和成熟，列车自动化系统将进一步优化铁路运输系统，减少制动和加速操作的频率，进而减少运行轨迹控制偏差成为研究重点，据此，提出了一种追踪间隔时间优化下的自动驾驶运行高可靠性优化方法。

1 列车群运行状态控制参数获取

1.1 线路附加阻力和运输线路条件的关联度分析

设定共有n列高速列车从始发站依次发车，从始发站到终点站共有m个区间，单一列车在单区间的运行状态如公式（1）所示：

式中：

N—列车运行的历史质量评价值；

β—列车的回转质量系数；

t—列车的运行时长；

v(x,y)—单一列车在当前的行驶速度；

a1、a2—列车的牵引力和制动力；

B1、B2—牵引系数以及制动系数；

Bas、Bbs—列车运行过程中的基本阻力以及附加阻力。

在列车运行过程中，列车的牵引以及制动工况两者是互相排斥的，所以，B1和B2需要满足公式（2）所示的约束条件：

在列车自动驾驶运行过程中[6-7]，列车所受到的阻力和列车的行驶速度等存在关联，同时线路附加阻力和运输线路条件的关联度如下所示：

式中：

c0、c1、c2—戴维斯方程系数；

φk—列车在设定时间段内第k段坡道对应的坡度信息；

e(k)—列车在当前时间段内第k段曲线的半径；

E(x,y)—当前位置第k条隧道的长度。

1.2 多智能体列车群分布式信息交互下的参数获取

多智能体列车群的信息交互则是为了实现列车之间的协同与合作。分析线路附加阻力和运输线路条件的关联度，可以提供重要的参考信息来优化列车群的信息交互过程。将列车的全部运行过程看作是一个系统，整个系统是由多个不同的智能体组成。在系统中，每个单一的列车i都为一个智能体Ri。为了确保列车在自动驾驶状态下具有较高的运行可靠性，优先获取列车在各个线路的运行状态以及最佳驾驶策略等信息，通过各个列车之间的网络拓扑结构[8,9]来表示列车之间的关联和通信，形成如公式（4）所示的有向图G：

在这个有向图中，RG代表由全部顶点组成的集合；DG代表图中由全部边组成的集合。根据网络拓扑结构，列车可以通过与邻近列车的通信了解周围环境及其他列车的状态信息，通过交换和共享阻力和速度信息，列车可以根据当前线路上不同位置的阻力情况。有向图中，各个顶点之间的作用关系σij可以表示为公式（5）的形式：

式中：

(Ri,Rj)—智能体顶点i和j之间的邻接关系。

在上述分析的基础上，通过图1给出列车群的信息交互过程。

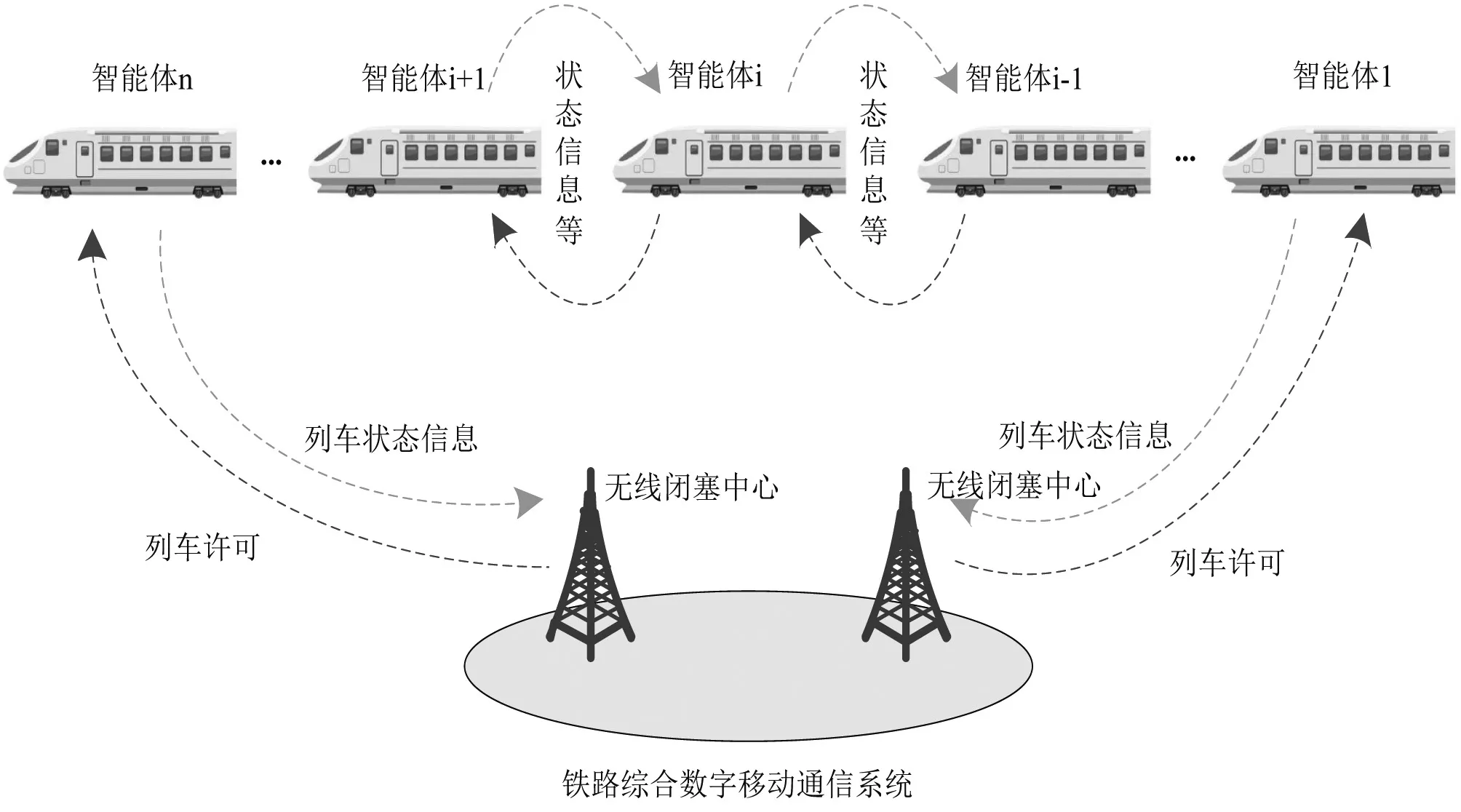
图1 多智能体列车群分布式信息交互示意图

通过多智能体列车群的分布式信息交互，可以实时收集列车的位置、速度、加速度等运行状态参数。

1）通过轨旁设备以及全球卫星导航系统可以实时掌握列车在各个时间内的运行情况，获得列车实时位置参数τ。

2）在列车运行状态下，各个列车之间的运行状态等相关操作是可以实时交互的，同时根据列车追踪技术可以得到列车的行驶速度参数v(′x,y)。

3）在存在干扰的情况下，全部列车在相互通信的基础上，通过相关的优化算法调节不同列车的驾驶策略，有效消除延误，获取列车加速度状态参数ϑs。

τ、v(′x,y)、ϑs可以用来计算最短追踪间隔时间、运行能耗和运行轨迹控制偏差。这些参数作为后续列车自动驾驶运行控制系统的关键部分，参数的准确性和优化程度将直接影响到自动驾驶系统的性能和运行效果。

2 自动驾驶运行高可靠性控制优化

2.1 约束条件与控制目标函数设置

在复杂、多变的交通环境中，面对异类情况和突发事件，如恶劣天气条件或信号灯故障，自动驾驶系统的信息感知能力和应对策略仍存在挑战，分布式信息交互过程与运行高可靠性控制优化过程需要更精细和多样化的约束条件。

列车在自动驾驶过程中，需要根据行驶线路选择对应的自动驾驶策略，不同区间的运行能耗和运行时间存在较大差异，以此设列车的最优自动驾驶控制运行策略是由多种不同工况组成的，在实际运行过程中，设定列车的初始速度和巡航速度为v(0)和v(a)，将两者作为决策变量，为了确保列车自动驾驶的安全性，考虑如下约束条件，分别为：

式中：

v(max)—列车的最快运行速度；

Qs—列车i和前车之间的最小安全距离；

P(d,i)—列车i之间的实际追踪距离；

U(i,j)—乘客舒适度。

以最短追踪间隔时间、最小运行能耗以及最小运行轨迹控制偏差为优化控制目标函数Ik*(ux,uy)：

式中：

Tx,y—追踪间隔时间；

Hx,y—列车运行能耗；

ϑs—基于列车加速度状态参数，

Wx,y—通过比较实际行驶轨迹与理想轨迹的差异来分析运行轨迹控制偏差。

2.2 控制过程中目标函数求解

多智能体列车群分布式信息交互过程涉及列车的速度控制、加速度和制动过程性信息，即多优化目标函数组合在一起才可以达到列车最优运行状态，而最小安全间隔时间与追踪间隔时间存在直接关系，由此，需要分析追踪间隔时间有效性，进一步进行自动驾驶运行高可靠性控制优化。

人群搜索算法作为一种群体智能搜索算法，将其应用到追踪间隔时间有效性分析中，进而确认列车运行规律。

1）对全部参数设定初始化处理，主要包含列车的线路信息以及列车基本参数等相关信息，同时将迭代代数的取值设定0。

2）设定列车群内共有n列车，以第2～n列列车的初始速度和巡航速度作为决策变量，设定决策变量的搜索范围，同时对种群展开初始化处理，种群的规格为N×2(n-1)，则有：

式中：

V—列车的基本运行速度参数；

H—列车的线路运行轨迹；

Xt—在t时段内的群体；

N—粒子数量；

Hn—第n辆列车的线路运行轨迹；

—在t时段内第i个体和第k个个体之间的决策变量。

3）对每个个体Xt展开自动驾驶运行轨迹控制处理。

4）应用模糊系统对列车运行过程中的不确定行为展开模拟分析[10-13]，进而确定适应度函数和搜索步长两者之间的关联性，获得列车位置、速度、停站时间等信息。其中，搜索步长αi,j可以表示为公式（10）的形式：

式中:

δi,j、ui,j—设定维数空间下的高斯隶属函数和高斯隶属度。

其中，高斯隶属函数的参数对应的计算式如下所示：

式中：

xmax和xmin—全局最优以及最差位置；

tm—第m辆列车的运行时间；

ω代表惯性权重。

在确定搜索步长以及搜索方向以后，需要对不同个体展开更新处理，详细的计算式如下所示：

式中：

xi,j(t+1)—在t+1时段内的决策变量[14,15]；

di,j(t)—在t时段内个体i和个体j之间的距离。

5）通过随机加权方式，确定最终的搜索方向，对应的计算式如下所示：

式中：

dij,ego(t)—利己方向；

dij,alt(t)—利他方向；

dij,pro(t)—预动方向；

ω1(t)—在t时间段内的第一个惯性权重。

确定自动驾驶的搜索策略，计算各个列车在每一维决策变量的搜索方向以及步长。

6）更新每辆列车的位置信息。

7）判断是否达到设定的最大迭代次数，假设是，则直接进入到下一步；反之，则跳转至步骤（3）。

8）判断自动驾驶控制的追踪间隔时间有效性，假设优化方案满足公式（6）与B1B2=0，完成全间隔标准调整以及运行参数高可靠性优化，则直接输出最终自动驾驶运行控制方案，据此计算每个个体的适应度函数，将适应度函数Φ(j)作为评价标准，判断各个自动驾驶运行高可靠性优化方案的优劣：

式中：

H0—列车在初始阶段的运行能耗；

Ti,k—第i辆列车和第k辆列车之间的追踪间隔时间；

Tsch—列车的平均追踪间隔时间。

反之，则跳转至步骤（1）。

通过确认与优化追踪间隔时间，列车之间更紧凑但仍保持安全的距离，减少制动和加速操作的频率，有效控制运行轨迹控制偏差，从而增加线路的运行容量和运力利用率，完成自动驾驶运行高可靠性控制优化。

3 实验

为了验证所提追踪间隔时间优化下的列车自动驾驶运行高可靠性控制优化方法的有效性，以Y城市某路段为测试对象，包括直线段、曲线段和坡道段，时间戳为2021年7月10日 09∶00∶00，列车速度为50 km/h，加速度为0.5 m/s²，在100公里的行驶路程中，平均能源消耗为30单位/公里。收集了1 000个地铁车辆间的样本数据，并规定最小安全间隔时间为80 s。

依据Y城市从L1到L8站的列车线路信息，生成样本数据，当两辆地铁车辆之间的时间间隔小于180 s时，认为发生了安全距离违规。在1 000个样本数据中，共有15次间隔时间小于180 s，因此存在15次安全距离违规。

为了验证各个方法的自动驾驶运行高可靠性，分别采用不同方法展开自动驾驶运行高可靠性优化处理，即设定对比方法为列车ATO运行多目标优化方法（文献[3]方法）和基于模拟退火算法的自动驾驶运行优化方法（文献[4]方法）

1）自动驾驶运行高可靠性控制测试分析

在设定时间范围内，通过图2给出各个方法控制下的列车自动驾驶运行情况。

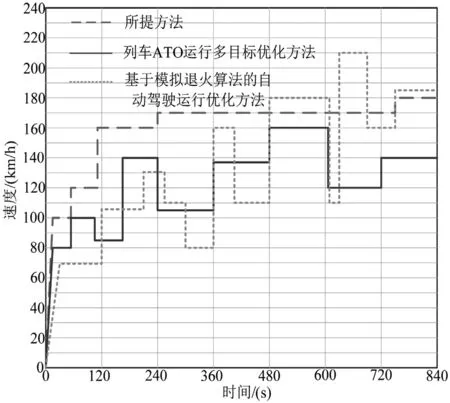
图2 不同方法的自动驾驶运行情况实验比较

分析图2可知，在设定时间范围内，采用所提方法可以确保列车在自动驾驶状态下的稳定运行；而采用另外两种方法对列车展开运行优化处理后，列车整体的运行速度一直处于忽高忽低的状态，无法有效确保列车在自动驾驶过程中的可靠性。由此可见，采用所提方法可以更好地确保列车在高可靠性状态下自动驾驶。

2）追踪间隔时间测试

通过表1给出各个方法的最短追踪间隔时间测试结果：

表1 不同方法的最短追踪间隔时间测试结果比较

分析表1可知，所提方法获取的最短追踪间隔时间明显低于另外两种方法，充分验证了所提方法的优越性。

3）自动驾驶运行能耗测试

为了进一步验证所提方法的优越性，在设定工况的情况下，需要对各个方法的自动驾驶运行能耗展开测试分析，详细的实验测试结果如图3所示。

从图3能够看出，各个方法对应的列车自动驾驶运行能耗会随着实验次数的增加呈现上升趋势。但是与另外两种方法相比，所提方法的列车自动驾驶运行能耗明显更低一些，说明通过所提方法可以有效减少自动驾驶运行能耗，同时也证明所提方法更加适用于优化自动驾驶运行的研究。

4）运行轨迹控制偏差测试

为了更进一步验证所提方法的性能，实验在设定时间情况下对各个方法的列车运行轨迹控制偏差展开测试分析，列车运行轨迹控制偏差取值越小，说明列车自动驾驶过程中可靠性越高；反之，则说明；列车自动驾驶过程中可靠性越低，详细的实验测试结果如图4所示。

图4 不同方法的运行轨迹控制偏差实验结果比较

分析图4可知，在运行时间不断变化的情况下，各个方法对应的运行轨迹控制偏差也在不断发生变化。和另外两种自动驾驶运行高可靠性优化方法而言，所提方法获取的列车运行轨迹控制偏差最低，说明所提方法可以更好地控制列车运行轨迹，同时也证明采用所提方法可以得到更加满意的自动驾驶运行高可靠性优化方案。

4 结束语

本文提出了一种追踪间隔时间优化下的自动驾驶运行高可靠性优化方法，重点确认与优化了最优追踪间隔时间，降低列车运行轨迹控制偏差，得到更加满意的自动驾驶运行高可靠性优化方案，使得列车能够更精确地遵循行车规程，保持与前后列车之间的安全距离，并在高密度、高速度的线路上实现高频率的列车运行。

未来阶段，可以对列车自动驾驶过程中的运行调整过程展开分析，同时还需要考虑定位精度以及列车通信延时等对列车运行安全产生的影响，进一步提升列车运行的安全性和可靠性。