基于自然场景统计的图像质量评价算法

秦小倩，杜 浩

（1.桂林学院，广西 桂林 541006；2.桂林电子科技大学，广西 桂林 541004）

0 引 言

图像信息是人类获得外部信息的主导方式，这也是人类互动的重要组成部分。但是，由于传输环境的影响，操作不当以及设备在图像采集、处理、压缩、传输和重建等过程中，图像很容易受损从而给图像研究带来了很大的困难[1-2]。因此，如何准确评估图像质量已成为图像处理领域的研究热点。图像质量评价方法分为主观和客观质量评价方法，主观质量评价方法指的是利用人类的视觉感知对图像进行评价，需要大量的人类参与，因此它是最准确可靠但又繁琐耗时的。客观的图像质量评价方法是通过建立数学模型描述图像质量，达到与人类主观感受近似一致的目的，主要分为3 个类别[3]：全参考图像质量评价方法（FR-IQA）、半参考图像质量评价方法（RR-IQA）、无参考图像质量评价方法（NRIQA）。全参考和部分参考图像质量评价方法都需要受损图像与其对应的无损图像进行对比，而无参考图像质量评价方法在评价过程中不需要与对应的无损图像对比，具有更广泛的研究和应用价值。

当前，无参考图像质量方法有三个主要研究的方向：

1）用于指定失真类型的方法，该方法根据失真特性建立指定失真模型评估图像质量。例如，对于模糊失真，文献[4]通过模糊图像的结构被破坏程度建立模型描述图像的质量评估值；对于压缩失真，利用在小波系数的对数域中具有近似线性规则，并且通过已建立的联合直方图模型获得图像质量指标[5]。

2）基于机器学习的方法，该方法取决于提取影响图像评估质量的图像特征的能力，再使用机器学习领域已有算法构建模型[6]。如使用SVR 导出失真图像的特征进而评价图像质量[7]、基于通用深度神经网络算法预测图像质量[8]。

3）基于NSS 模型的方法，自然图像都会有其固定特性，而失真会改变这些特性。例如，文献[9]通过提取失真图像改变的NSS 特性建立模型进行图像的质量评估。文献[10]提出了BLIINDS 算法，该算法从DCT 域中提取4 个NSS 特征并训练它们，获得图像的质量评价指标。BLIINDS-Ⅱ[11]在BLIINDS的基础上引入了离散余弦统计特征对图像质量进行评价。文献[12]基于图像在小波域中遵循非高斯分布的NSS 特性，进行图像质量的评估（BIQI）。Mattal.A 提出使用广义高斯模型描述失真图像的预测参数和实际参数之间的差异来进行质量评价（NIQE）[13]。

本文提出一种基于NSS 的无参考图像质量评价算法，使用图像的低尺度子带能量预测高尺度子带能量，并用各尺度能量的预测值和失真图像实测值的差异来度量失真图像的质量。

1 图像的自然统计特性

1.1 小波变换

二维离散小波变换（DWT）通常在实际图像处理中使用，通常分别以行和列方向提取二维信号[14]。二维小波分解图如图1 所示。

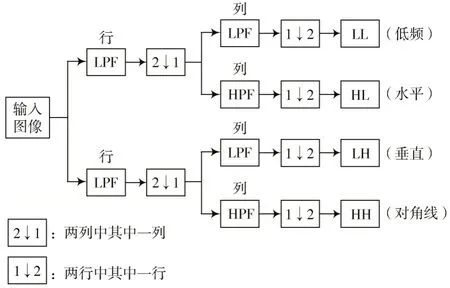
图1 二维小波分解图

输入图像利用一维低通滤波器（LPF）和高通滤波器（HPF）进行行滤波，再通过相同的方法进行列滤波，得到4 个不同的频率子带（低频信息LL、垂直信息LH、水平信息HL 和对角线信息HH）。在小波变换中，图像的近似信息和细节信息分别以低频组件（LL、HL、LH）和高频组件（HH）表示。由于低频成分蕴含了信号的主要特征，因此小波可以进一步分解图像近似部分（LL），获得更多的低频成分。图2 为图像的3 级小波分解结构图，其中，1、2、3 表示小波的分解尺度。

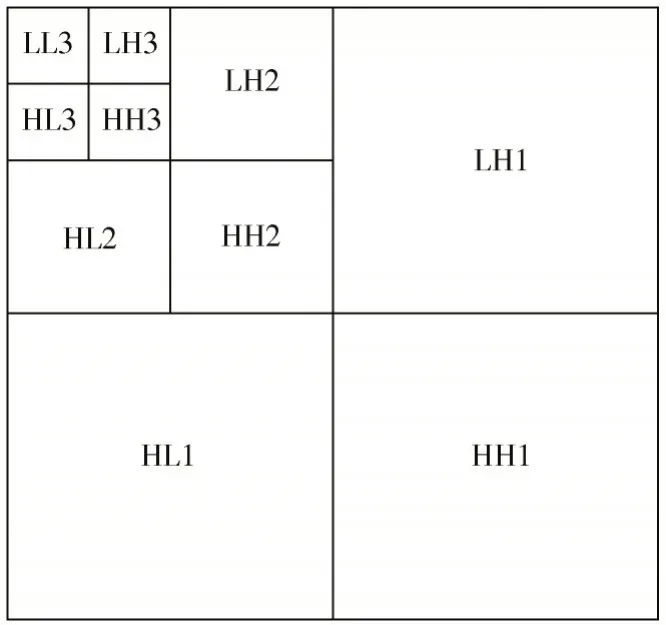
图2 3 级小波分解结构图

1.2 自然图像的小波域统计特性

由于自然图像具有不同的视觉感知区域（即边缘、纹理、平坦和其他区域），因此在自然图像中会出现某些频率分布特性[15]。对数域中自然图像的功率谱与空间频率之间存在近似线性关系，即随着分解级数的增加，对数域中小波子带能量呈线性减小。子带能量表示为[16]：

式中：E为子带能量；N是相应子带的像素点序号；C为子带系数；s是分解的级数；o表示方向；φ是调节因子。

图3 为4 级小波分解各子带能量序号，图4a）表示了LIVE 图像质量评价数据库[17]中29 张自然图像经过4 级小波分解后各子带在对数域的能量分布。子波能量具有近似线性减小的规律，但是其形状并不光滑，这是由于不同的图像具有不同的内容，不同图像的能量谱差异大。

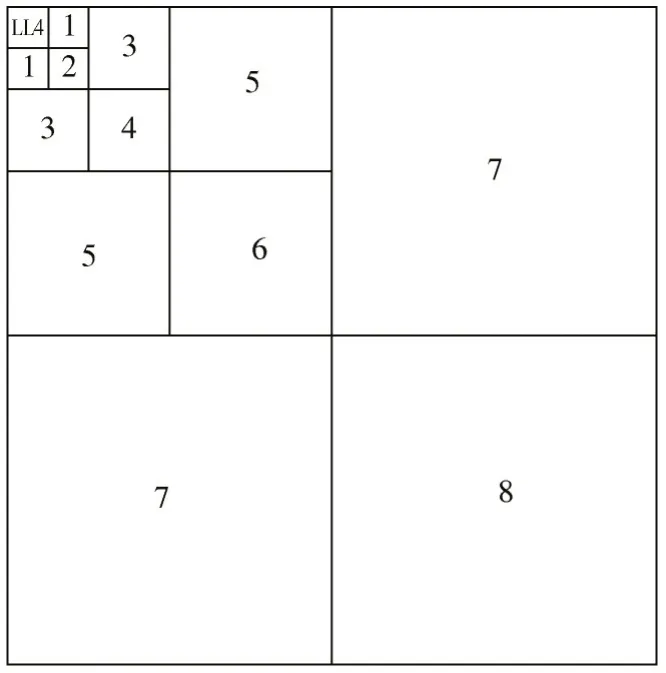
图3 小波子带能量序号

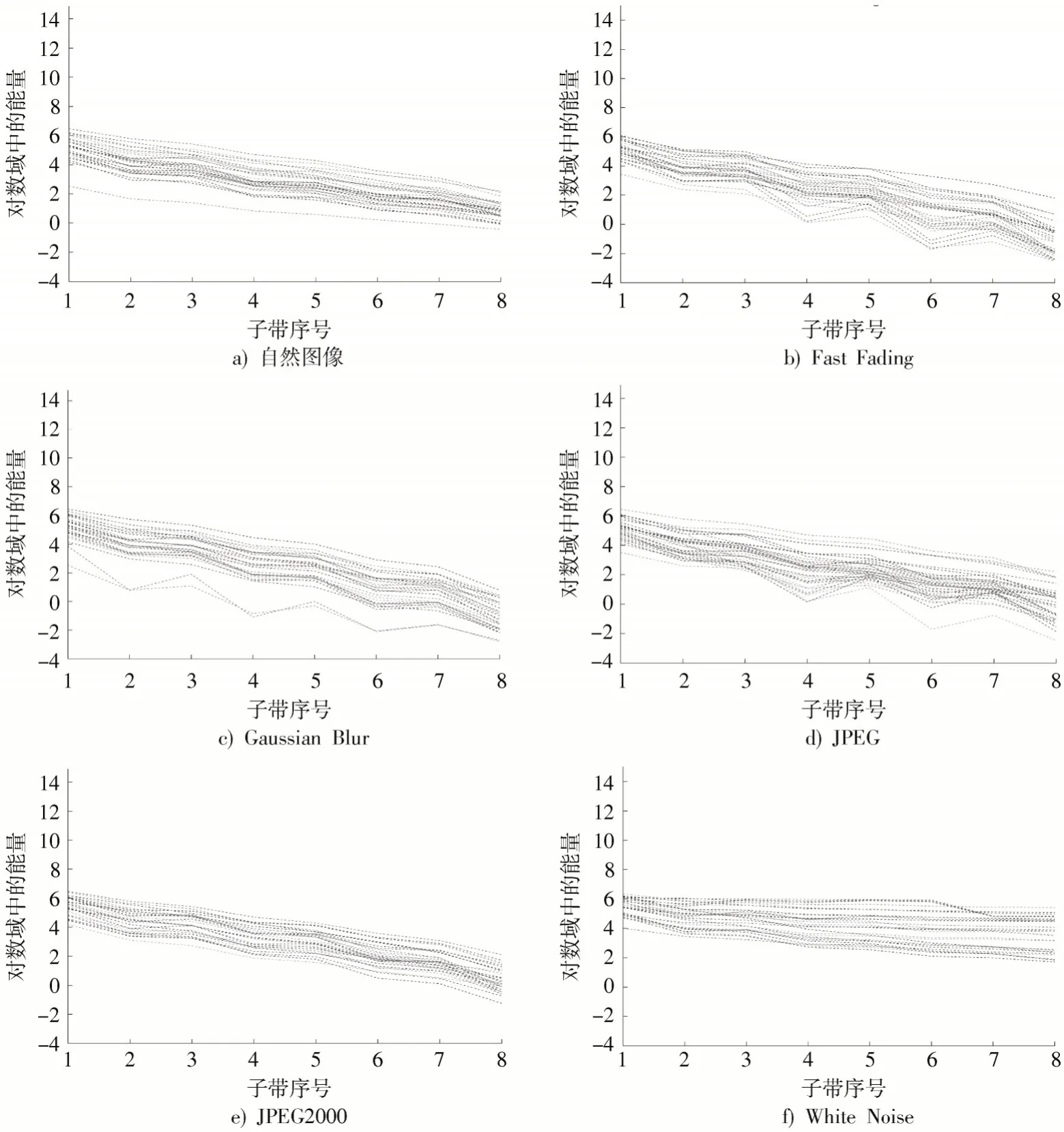
图4 自然图像和各失真类型的图像在小波域中各小波子带与能量的关系

1.3 失真图像的自然统计特性

振铃效应、模糊效应、随机噪声等是图像处理中常见的使图像失真的原因，它们将影响图像的高频信息[18]。JPEG2000，JPEG，White Noise，Gaussian Blur和Fast Fading为图像常见的失真类型，图4b）～图4e）显示了各失真类型在对数域中各小波子带与能量的关系，其中每种失真类型在LIVE图像质量评价数据库随机选取29幅图。

可以看出，所有失真类型的图像体现出NSS 特性：小波高尺度变换下的低频子带小波能量（子带No.1 和子带No.2）衰减较慢或者不衰减，但低尺度变换下的高频子带（子带No.3～子带No.8）衰减较快但不完全一致。这是由于失真类型的不同，图像失真的部分与程度也不同。由于图像的NSS 特性变化可以反映图像的质量变化，因此利用失真图像的NSS 特性受影响程度来表示失真图像的质量。

2 基于NSS 的图像质量评价算法

从自然图像和失真图像的NSS 特性可以看出，自然图像经小波多尺度分解后的子带能量在对数域中具有强线性规律，而失真图像则打破了这一规律。对于失真图像，失真主要表现为表细节的低尺度（高频带序号）的子带能量部分有显著变化，而表近似的高尺度（低频带序号）的子带能量部分几乎没有变化。使用自然图像的高尺度子带能量预测低尺度子带能量，并用各尺度能量的预测值和失真图像实测值的差异来度量失真图像的质量。由于自然图像和失真图像中子带能量的线性特性在4 级小波分解中表现明显，因此在该方法中采用4 级小波分解。

4 级小波分解算法流程图如图5 所示，共分为以下几部分。

图5 算法流程图

1）训 练

为了描述自然图像子带能量的线性规律，从训练N（N＞20）幅自然图像中得到线性预测矩阵M(s)，使高尺度的子带能量（子带No.1 和子带No.2）可以预测低尺度的子带能量（子带No.3～子带No.8）。首先，在N(N＞20)幅原始无损的图像上，根据式（2）得到原始图像的子带能量矩阵IE(n,s,o)；然后，利用最小二乘法的矩阵变换得到预测矩阵M(s)。

式中：s是尺度数，s= 3,2,1；M(s)表示s尺度上的预测矩阵；IE(n,s,o)是自然图像的s尺度上的子带能量；n是原始图像的数量，实验中n= 29；o表示每层的方向；IE(n,4,o)是自然图像的第4 尺度的子带能量。

2）预 测

根据式（3），通过小波变换获得失真图像的子带能量DE(s,o)，再通过失真图像的第4 尺度的子带能量DE(4,o)与预测矩阵M(s)相乘得到相应的预测无失真子带能量PE(s,o)。

式中：s是尺度数，s= 3,2,1；o表示每层的方向。

3）调 整

如图4c）所示，当图像失真严重时，高尺度子带（子带No.1 和子带No.2）的能量DE 会发生很大变化。如图6a）所示，如果用这些波动的值进行预测，将产生显著的误差。因此，预测值PE 被调整以防止这种情况发生，如式（4）、式（5）所示：

图6 调整前后失真图像各子带的预测能量变化

式中：s= 3,2,1；(IE(n,4,o))min是步骤1）中的29 个自然图像第4 尺度的子带能量的最小值；(IE(n,s,o))mean是自然图像第s尺度子带能量的平均值。调整后的能量分布如图6b）所示。

4）使用CSF 模型构建加权系数

对比敏感度是HVS 的一个显著特征，指人眼对图像中不同区域的敏感度，它随着视觉场景中的空间频率而变化[19]。因此，对比敏感度随空间频率变化的曲线称为CSF。由于人眼在不同程度上可以感知不同的空间频率，因此对不同频率的子带使用CSF 模型进行加权，使其更接近HVS[16]。各尺度的加权系数如式（6）所示：

式中：fr=fn*fs表示人眼视觉范围内的空间频率，fs为采样频率，fn为归一化频率和fy分别是图像的水平频率和垂直频率。根据文献[16]计算出各相应子带序号所对应的加权值如表1 所示。

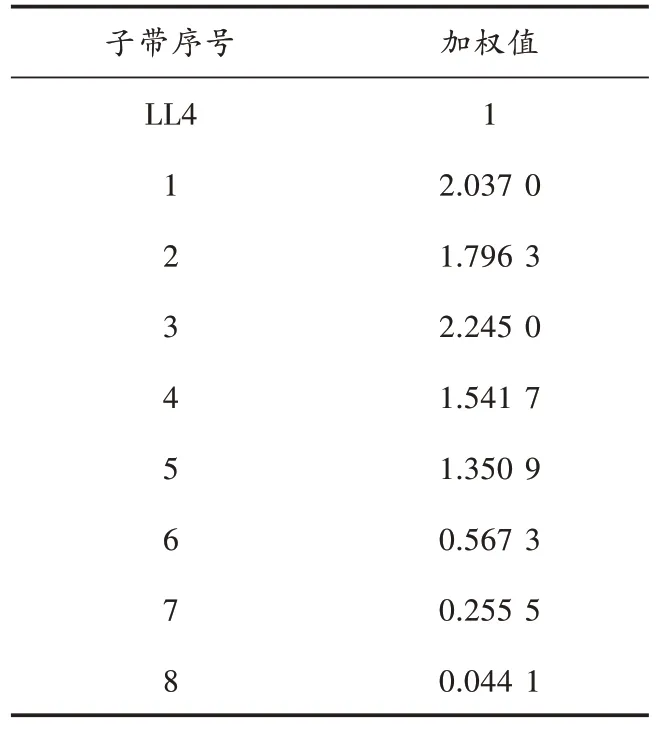
表1 各子带序号所对应的加权值

5）图像质量评价值Q

如图7 所示，通过失真图像中每个子带的预测值PE和实际值DE 之间能量差的加权和（见式（7））获得图像质量评估值Q。

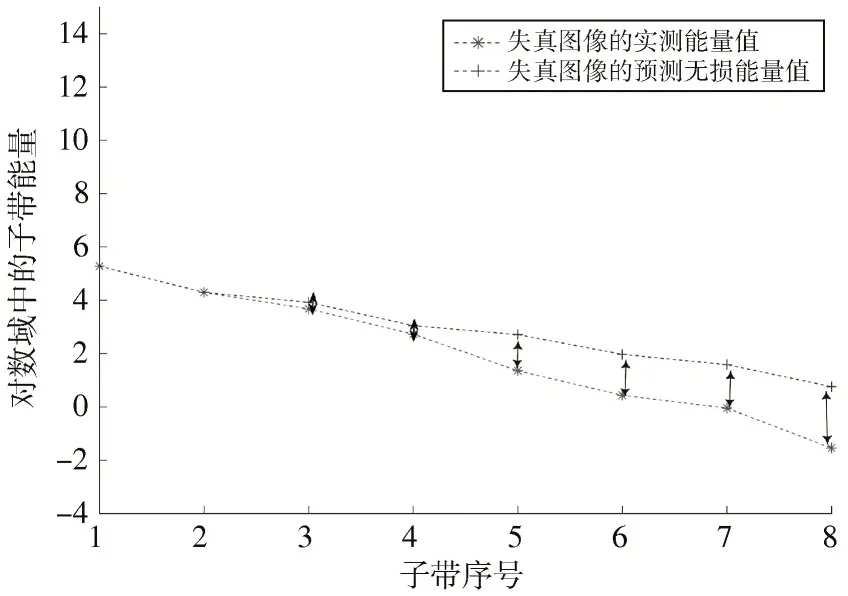
图7 失真图像在各子带中所预测无失真能量和实际能量之间的能量差

式中：A是每个尺度中两个方向的权重，在实验中，水平和垂直方向A= 1.1，对角线方向A= 0.9；As是通过CSF模型获得的每个尺度的权重系数；PE(s)是受损图像的预测无损能量；DE(s)是受损图像在s尺度上的实际能量。该图像的质量分数Q越高，失真图像的失真程度越高，则图像质量越低。

3 实验结果与分析

3.1 独立数据集验证

本文提出的算法在LIVE 图像质量评估数据库上进行测试。在LIVE 数据库中，有29 幅不同分辨率的原始图像和779 幅由这些原始图像生成的5 种不同类型的失真图像，分别是：JPEG2000（JP2K）169 幅；JPEG175 幅；White Noise（WN）145幅；Gaussian Blur（GBlur）145幅；Fast Fading（FF）145幅。同时，该数据库提供了所有失真图像的平均主观意见得分差异（DMOS）值。实验中，该数据集被分为训练集和测试集，训练集由29幅原始图像来形成预测矩阵，测试集由各失真类型的750幅图像组成。

该算法的客观质量评价得分与图像数据集提供的主观DMOS 值之间的一致性程度作为该算法的性能度量。本实验利用2 个客观评价值作为算法的性能指标。

秦汉魏晋南北朝时期的丞相…………………………………………………………………………………………甄 鹏（3.33）

1）线性相关系数（LCC）：通过算法的客观质量评价值与主观DMOS 值的相关性来表示算法的准确性。

2）Spearman 等级相关系数（SROCC）：反映算法的客观质量评价值单调性的一致性。LCC 和SROCC 的值在0 和1 之间，值越高，表明算法与人眼的一致度越好，则算法的性能越好。

3.2 结果与分析

3.2.1 单个数据库验证

本文算法在LIVE 数据库上运行，图8 显示了各失真类型和全失真类型的客观质量评价分值和主观DMOS 值的散点分布图，图中的每个点表示要评价的图像。在理想条件下，客观评价值与主观DMOS 值之间存在一对一的关系，表现为直线或曲线。散射的点越是收敛到一条直线或曲线上，算法的性能就越好。从结果中可以看出，对于JPEG、GBlur、FF失真类型的图像，算法的客观值与主观值具有良好的一致性。对于WN 类型失真的图像，算法的客观值与主观值具有高度的一致性。

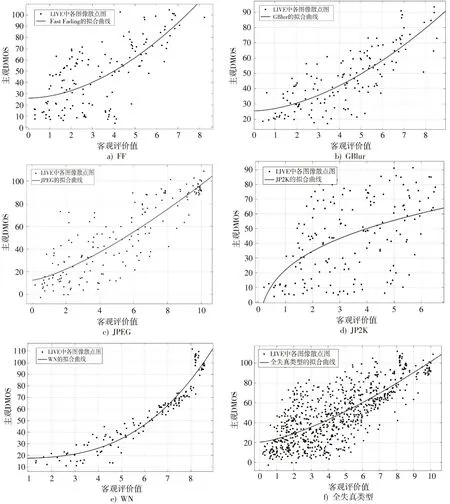
图8 算法客观评价值与主观DMOS 的散点分布图

表2 和表3 分别表示本文算法与现有算法的LCC 值和SROCC 值的比较。从表中可以看出，对于WN 失真类型的图像，本文算法的性能与BLIINDS-Ⅱ算法性能接近并远远优于NIQE 算法，与人眼具有高度的一致性；对于JPEG、FF、GBlur 失真类型的图像，本文算法的性能与BIQI 性能接近，与人眼具有良好的一致性；但本文算法在评价JP2K 失真类型图像质量方面较差，这是由于JP2K 较JPEG 压缩技术计算更复杂，从而造成图像的高频信息由于模糊效应而丢失，还由于振铃效应在高频子带中增加了许多噪声信息，导致各子带无失真能量的预测有较大的误差。

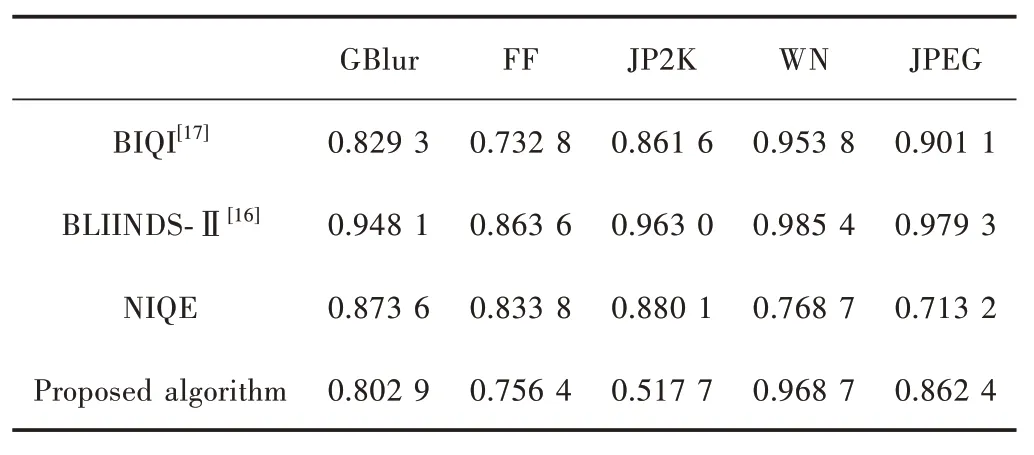
表2 本文算法与其他算法在各失真类型中的LCC 比较

3.2.2 跨数据库验证

由于本文算法主要在LIVE 数据库上进行验证，即在LIVE 数据库中获取训练集和测试集，因此需要用CSIQ 数据库[20]来验证本文算法对数据库的敏感度。

本文设计实验如下：

1）使用LIVE 数据库中的29 幅原始图像作为训练集，使用CSIQ 数据库中各失真类型的图像作为测试集；

2）使用CSIQ 数据集的30 张原始图像作为训练集，LIVE 数据集中的各失真类型的图像作为测试集。

表4 为各算法对于全失真类型的性能指标（SROCC值）。结果表明，本文算法对数据库的敏感度较低，算法稳定性较好并优于BIQI 算法。

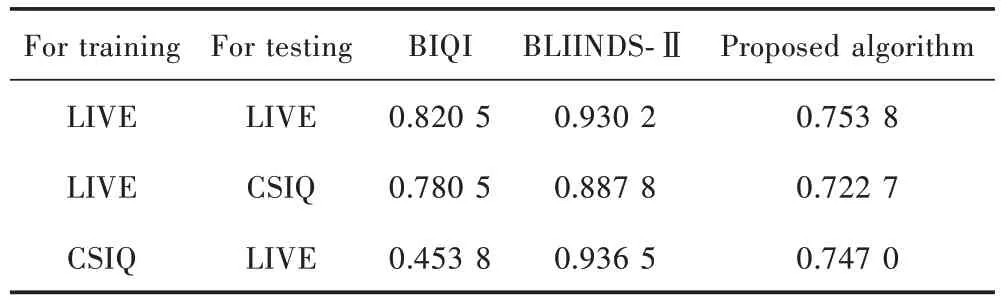
表4 各算法在跨数据集的验证（SROCC 值）

3.2.3 时间复杂度验证

图像质量评价算法的时间复杂度是实际应用中的一个重要指标。表5 表示了各算法评价一幅分辨率为512×640 的图像质量的运行时间。实验在Matlab R2020A 中运行。实验运行平台是一台2.5 GHz CPU 和8 GB RAM的笔记本电脑，操作系统是64位Windows 10。

表5 各算法的运行时间

从表5 中可以看出，本文算法比BLIINDS-Ⅱ算法快得多。因此，从时间复杂度的角度来看，它在无参考图像质量评价应用中具有竞争力。

4 结 论

本文提出了一种基于NSS 的无参考图像质量评价算法。本文算法在评价JPEG、WN、GBlur、FF 失真类型的图像质量时与人眼具有良好的一致性，并且对全失真类型图像质量评价时，稳定性优于BIQI 算法，适用范围更广。特别是在对WN 失真类型的图像进行评价时，性能与其他算法一致，但运行时间远远小于BLIINDS-Ⅱ算法，具有很大的时间优势，适用于实时性强的工程运用中。然而，JP2K 失真类型的图像由于其复杂的形成过程而不适用于本文算法，因此，算法需要在JP2K 失真图像方向改进。

注：本文通讯作者为秦小倩。